基于高动态粒子冲蚀的火炮身管寿命研究

丁树奎,张领科,丁旭冉,于世勇,王戴思源,王 克

(1.中国北方工业有限公司,北京 100081;2.南京理工大学 能源与动力工程学院,江苏 南京 210094;3.齐齐哈尔和平重工集团有限公司,黑龙江 齐齐哈尔 161006)

火炮在发射过程中,身管不断承受高温高压火药气体的烧蚀、冲刷和弹丸产生的机械磨损的综合作用,使炮膛表面损耗,逐渐改变炮膛内部结构,从而使火炮内弹道性能发生变化,影响火炮身管寿命。长期以来,国内外学者对影响身管寿命的因素和机理进行了广泛的理论与试验研究[1-5]。传统理论认为发射药热作用、化学作用以及身管和弹带的机械作用是影响身管寿命的主要因素[6]。

磨损现象最严重的地方是在膛线起始位置[7]。但现有理论难以解释工程实践中的一些基本现象,比如在同样的热和化学作用下,不和弹带直接接触的坡膛部分也会出现严重的皲裂和减材现象,而药室的圆柱部分却没有这些现象发生。笔者认为,膛内高温高压燃气与固体药粒在坡膛处由于高速运动且和速度方向与壁面之间有一定的夹角,造成了膛线起始部位的严重冲刷磨损。

冲蚀是流体中固体颗粒以一定的速度和角度冲击材料表面[8-9],发生碰撞并造成材料损失的一种现象[10]。FINNIE等[11]提出了一种动态粒子对塑性金属材料的冲蚀微切削理论。该理论将动态粒子视为一把微型切刀,当粒子碰撞并划过材料表面时,材料被“切除”而产生损失,导致材料表面形成一定的冲蚀量。鉴于冲蚀是一个动态的过程,冲蚀量通常采用冲蚀速率来描述[12],进而通过冲蚀速率计算出动态冲蚀量。研究表明,颗粒形状对侵蚀程度有显著影响,SALIK等[13]将颗粒形状对冲蚀量的级别进行了划分。LEVY等[14]的研究也证明了不同的颗粒形状对冲蚀量影响程度存在较大差别,特别地,锐角形的颗粒冲蚀率是圆形颗粒冲蚀率的4倍。王斐等[15]将含微量纳米硬质颗粒的实验药与制式药进行对比射击试验。结果表明,纳米硬质微粒对枪管内壁有极大的破坏作用,间接证明硬质火药残渣对枪炮管存在一定的破坏作用。

目前,火炮主要采用单发内膛直径扩大量作为身管寿命评估标准[16-17]。本文结合内弹道理论和传热学理论,提出了一种基于高动态粒子冲蚀机理的新方法,研究了冲蚀速率与内膛直径扩大量之间的关系,为火炮寿命的评估和强化提高寿命提供了一个新的视角和途径。

1 高动态粒子对炮膛的冲蚀模型

在火炮内弹道过程中,发射药燃烧过程形成发射药产物气体-未烧完的发射药颗粒的气固反应两相流,随着发射药持续燃烧,在产物气体的推动下发射药颗粒速度不断增大,温度不断升高,药室内压强不断增大,形成高温、高压和高速的高动态粒子。高动态粒子与壁面之间发生随机碰撞,造成对炮膛内壁壁面的冲蚀作用。

1.1 物理模型

火炮膛内高动态颗粒膛内运动冲蚀示意如图1所示。

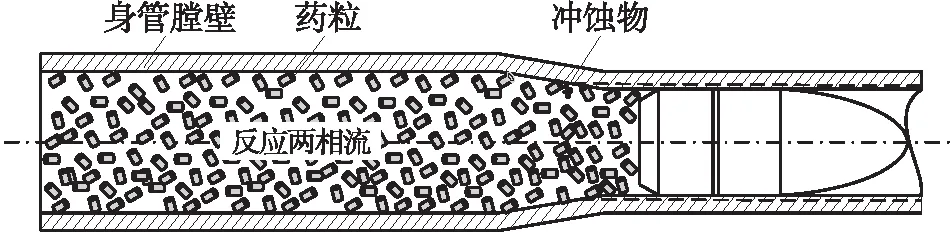
图1 火炮膛内高动态颗粒冲蚀示意图Fig.1 Schematic diagram of high dynamic particle erosion in gun bore

为了描述火药高动态粒子对炮膛内壁的冲蚀作用,提出如下基本假设:

①发射过程中弹后空间发射药密度均匀分布,即∂ρ/∂x=0;

②火药燃烧服从几何燃烧定律[18],即按平行层逐层燃烧,燃速是平均压力的指数函数;

③弹后空间火药与火药气体的质量分布是均匀的,速度和压力服从拉格朗日假设;

④火药气体服从仅包含余容修正项的诺贝尔状态方程,火药力f和比热比γ为常数,余容α为燃气密度的函数;

⑤将燃气视为双连续介质,燃气和颗粒速度相等,不同时刻药粒取当量直径作为特征尺寸;

⑥药粒瞬时尺寸一致且在弹后空间内均匀分布,即颗粒数只与位置有关;

⑦火药颗粒对壁面的冲蚀只与颗粒数目、壁面材料属性、速度和冲击角有关;

⑧火药颗粒对壁面的冲蚀作用限定在火药全部燃烧完成之前。

⑨弹丸开始运动以启动压力p0作为参考,次要功以次要功系数φ作为参考。

1.2 内弹道数学模型

①形状函数。

发射药燃烧百分数与形状特征量有关,对于复杂药型火药分裂点之前按三项式描述,分裂后按二项式描述,即:

(1)

式中:ψ为火药已燃百分数;χ,λ,μ,χs,λs为形状特征量;z为火药已燃相对厚度;zk为分裂后碎粒全部燃完时的燃去相对厚度。

②燃速方程。

(2)

式中:u1为燃速系数,e1为弧厚的一半,p为某一时刻的火药燃气压力,n为燃速指数。

③弹丸运动方程。

(3)

式中:φ为次要功系数,m为弹丸质量,v为弹丸运动速度,S为炮膛截面积,p0为启动压力。

④内弹道基本方程[19]。

Sp(lψ+l)=fωψ-(θφmv2/2)

(4)

⑤弹丸速度方程。

(5)

⑥弹后空间压力分布。

(6)

式中:p为平均压力;在所研究单元混合流体的相对坐标z=x/L,弹底到膛底的距离L=l00+l,l00为初始时刻弹底到膛底的距离。

⑦弹后空间燃气密度。

(7)

式中:ρg为平均密度,md为点火药质量。

⑧弹后空间温度分布。

(8)

式中:Tx为x处的温度,T1为爆温,T0为初温,xT为修正系数。

⑨空隙率。

(9)

式中:φ为孔隙率,np为包含在Aδx体积内的颗粒数目,Vp为单个火药颗粒的体积。

⑩火药颗粒特征尺寸。

考虑对壁面冲蚀作用的颗粒为多孔梅花形颗粒,当颗粒燃烧接近分裂,采用体积当量直径计算的直径不为0。为了使得颗粒在燃烧过程中当量颗粒保持原有的动量和动能,采用同等质量的等效球直径作为火药颗粒的直径dp,即:

(10)

式中:mp为单个火药颗粒的初始质量,ρp为火药颗粒的密度。

假设发射过程ti时刻火药颗粒粒径为dp,i,则:

(11)

式中:ψi为ti时刻火药的已燃百分比。

式(1)～式(11)构成了完整的火炮发射内弹道模型。首先,该模型基于朗格朗日假设,采用平均压力和瞬时恒定平均密度的方法,刻划了膛内温度沿轴向的分布规律,对于全装药情况下该方法计算的火药燃烧产生的燃气温度具有较高的准确性;其次,该模型建立了余容α与燃气密度的关系,使得燃气温度计算更接近膛内燃气变化的总体规律;最后,该模型建立了燃气中颗粒粒径与燃烧百分比的关系,忽略了燃烧不一致的情况,便于颗粒冲刷壁面时的仿真计算,减少了计算复杂度。

1.3 冲蚀数学模型

①冲蚀量模型。

影响冲蚀的因素比较多,主要包括颗粒速度、颗粒与壁面碰撞时的冲击角、颗粒粒径、形状、硬度、冲蚀材料性质等[20]。AHLER[21]根据不同冲击角度和不同形状固体颗粒对AISI 1018碳钢材料进行冲蚀实验,提出一个计算材料表面的E/CRC冲蚀速率(RE)模型,该模型适用于干燥和潮湿材料表面。

(12)

式中:RE为壁面冲蚀磨损速率,定义为壁面因颗粒冲击而损失的质量与冲击过程中的颗粒质量之比;C为壁面材料常数;HB为壁面材料布氏硬度;Fp为固体颗粒形状系数;n为速度指数;vp为固体颗粒冲击速度;f(α)为冲击角度函数。对于塑性材料,f(α)与冲击角的关系[22]：当α分别为0,20°,30°,45°,90°时,f(α)为0,0.8,1.0,0.5,0.4。

②冲蚀速率模型。

设PR为壁面材料的冲蚀磨损率,基于E/CRC冲蚀速率模型,考虑质量流率、壁面材料密度和计算单元的面积,则有:

(13)

③炮膛冲蚀量模型。

根据式(13)的壁面材料冲蚀率,设控制体内平均颗粒数为Np,有效作用于计算单元面积壁面的颗粒百分数为β,则平均冲蚀厚度Δd可表示为

(14)

式中:t1为控制体内开始有火药颗粒的时刻;t2为控制体内火药颗粒燃烧完全的时刻。综合式(12)～式(14)即为炮膛冲蚀量计算模型。上式中不考虑连续射击造成的温度累计上升带来的影响。

1.4 身管传热模型

身管壁面在高温燃气的作用下引起身管壁面的热软化、膛壁表面的热相变和膛壁表层的熔化。通过建立身管传热模型,基于内弹道参数获得膛壁温度变化情况,进而确定壁面材料特性参数。

基本假设:①忽略火药燃气同膛壁间辐射换热,仅考虑燃气同管壁对流换热;②忽略弹丸对膛壁的摩擦及其热效应;③忽略身管壁内热量的轴向传递;④温度场具有轴向及角度的对称性。

1.4.1 控制方程

采用一维常物性柱坐标系导热控制方程。

(15)

式中:T为身管壁面的温度,r为身管壁面中某点距身管对称轴的距离,a为身管壁面的导温系数,R0为身管内半径,R1为身管外半径。

1.4.2 定解条件

①初始条件。

t=0,取初始环境温度Tini=288 K。

②边界条件。

(16)

式中:T0为炮膛内壁的温度;TN为身管外壁的温度;Tout为外部环境温度,取288 K。

1.4.3 离散方程

时间项采用向前差分,空间项采用中心差分,对控制方程式(15)和定解条件式(16)进行离散化,离散示意如图2所示。图中,Δt为时间步长,Δr为空间步长。

图2 方程离散示意图Fig.2 Schematic diagram of equation discretization

①内节点差分方程。

(17)

②内边界差分方程。

(18)

③外边界差分方程。

(19)

式中:

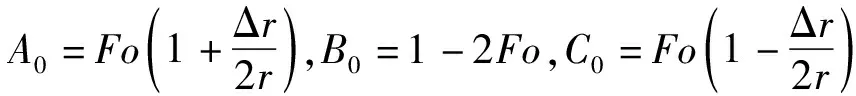
④稳定性条件。

1-2Fo>0

(20)

1.4.4 膛内对流换热系数

膛内燃气对流换热特征数方程可采用下式:

Nu=KeRe0.8Pr0.4

(21)

式中:Re为以身管内径为特征尺寸的雷诺数,Re=ρud/μ,u为燃气速度,d为身管内径,μ为动力黏度;Pr为普朗特数;Ke为入口修正系数,取:

Ke=-0.002 25z3+0.042 1z2-0.207 6z+1.870 8

(22)

式中:z=x/d,x为沿身管轴向坐标位置。

2 数值计算

2.1 基本参数

某155 mm火炮内膛坡膛附近示意如图3所示,计算仿真控制体位于膛线起始部前25.4 mm位置左右5mm范围内,装药类型为梅花23/19,基本参数如表1所示。

图3 火炮坡膛冲蚀计算控制体Fig.3 Erosion calculation control body of gun slope bore

表1 内弹道基本参数Table 1 Basic interior ballistic parameters

2.2 内弹道及燃气流动状态仿真结果

全装药情况下的内弹道燃气压力、弹丸速度及燃气密度随时间变化规律如图4所示,最大压力为330 MPa,最大初速为930 m/s。

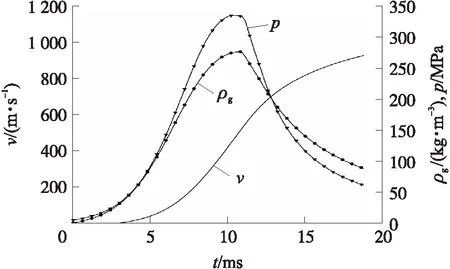
图4 内弹道特性参数变化历程Fig.4 Change history of interior ballistic characteristic parameters

针对炮膛膛线起始部25.4 mm处(控制体左边界)的雷诺数Re、普朗特数Pr、努塞尔数Nu进行了计算,由此得到了对流换热系数h随时时间的变化规律,结果如图5与图6所示;在此基础上结合传热模型计算得到了燃气温度和壁面温度随时间的变化规律,如图7所示。由图可见,燃气的温度先增加至最高温度约为3 318 K,随后降低;壁面温度控制体左边界有颗粒进入到火药颗粒燃烧完全的时间区间为4.5～11.85 ms,在此期间壁面的平均温度为833.9 K。

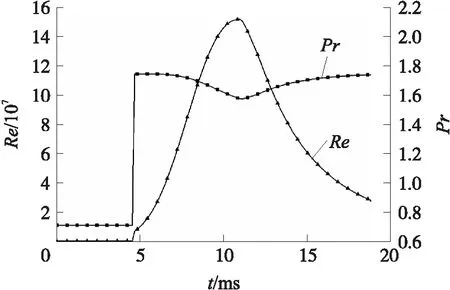
图5 雷诺数与普朗特数的变化规律Fig.5 Variation of Reynolds number and Prandtl number

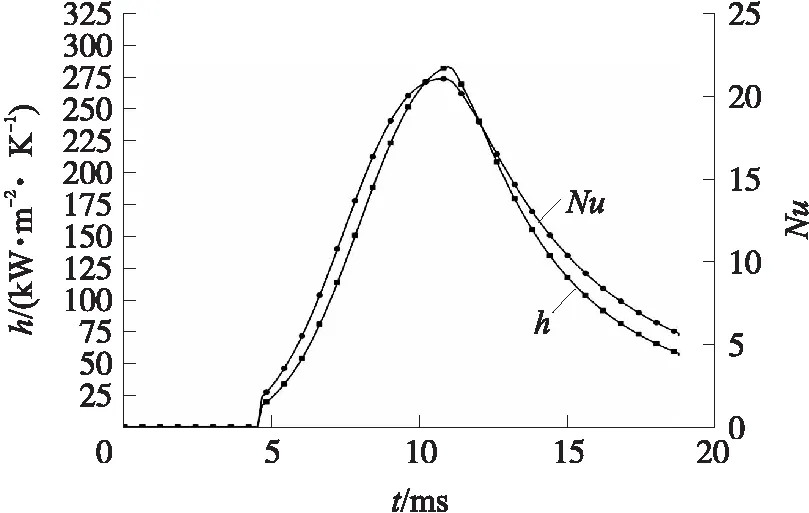
图6 努塞尔数与对流换热系数的变化规律Fig.6 Variation of Nusselt number and convective heat transfer coefficient

图7 控制体左边界处燃气温度和壁面温度曲线Fig.7 Variation of gas and bore wall temperature at left boundary of control body

2.3 冲蚀量计算

图8为某炮钢的布氏硬度HB随温度的变化规律[23-24]。可以看出,随着温度的升高,布氏硬度逐渐减小;当温度大于700 K时,布氏硬度与温度呈线性关系:HB=654.636 67-0.39T。

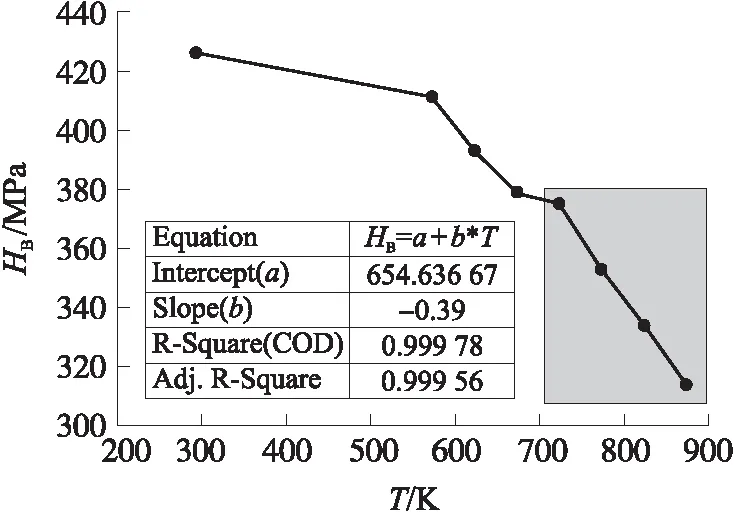
图8 某炮钢布氏硬度HB随温度变化规律Fig.8 Variation of Brinell hardness(HB)of a gun steel with temperature

图9 空隙率及粒子质量流率变化规律Fig.9 Variation of particle porosity and mass flow rate

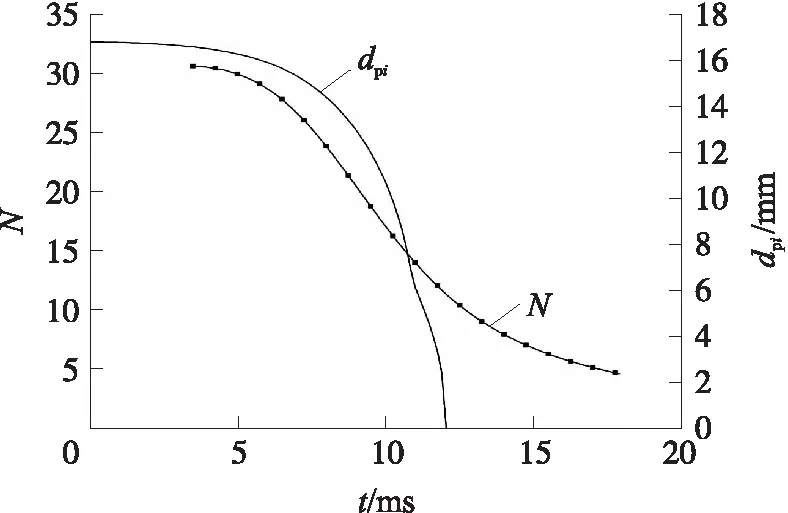
图10 平均粒径和颗粒数变化规律Fig.10 Variation of average particle size and particle number

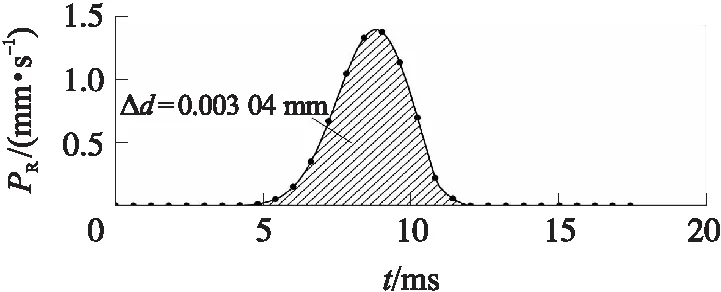
图11 冲蚀速率变化规律Fig.11 Variation of erosion rate

基于炮膛冲蚀量计算模型计算得冲蚀量Δd=0.003 04 mm,与该火炮在现有技术水平下的单发冲蚀量(约为0.003 mm)吻合较好。

3 试验验证

3.1 集流锥冲蚀假设模型

为了改善膛内气固两相流对身管壁的冲蚀作用,提出如下设想:在药室内增加集流锥结构,利用集流锥改变膛内高温高压两相流燃气的流动状态和固体火药颗粒的流动路径和方向,减少对膛线起始部的冲蚀效应,从而减缓其内径的扩大,其原理如图12所示。药室内的发射药颗粒在燃气的作用下不断向炮口移动,以高速火药颗粒P为例,当它运动到集流锥倒角处时与膛壁碰撞,速度大小和运动方向均发生了变化。接下来火药颗粒P继续运动,与其他药粒发生随机碰撞,能量及运动方向进一步改变,出现药粒越过坡膛起始部位置而减少对控制区域的冲蚀。

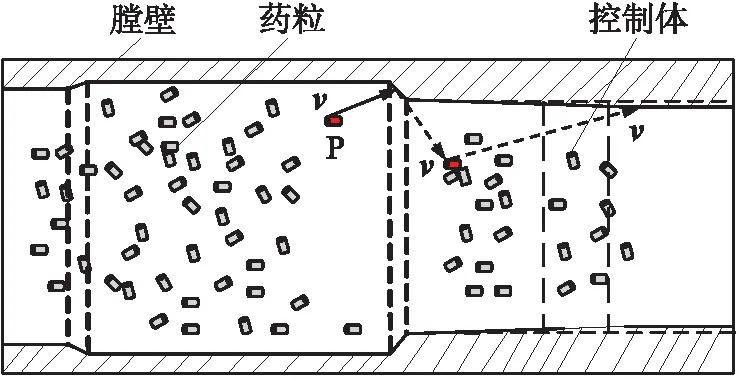
图12 身管集流锥药室结构Fig.12 Barrel collecting cone chamber structure

3.2 试验对象

为了验证集流锥结构能够减缓高速动态药粒对坡膛的冲蚀影响,以30°和40°的两种倒角的集流锥结构,如图13所示,并在弹道炮上进行试验。

图13 集流锥倒角结构示意图Fig.13 Schematic diagram of chamfer structure of collecting cone

3.3 试验结果

分别对倒角γ=30°和γ=40°两种集流锥结构在全装药情况下进行射击试验,并计算了单发平均冲蚀量Δd,试验结果如表2所示。测量采用多次测量求平均值的方式。

表2 身管冲蚀试验结果Table 2 Results of barrel erosion test

由试验表明,当集流锥锥角γ=0°,即无集流锥,平均单发冲蚀量Δd=0.003 04 mm。由表2可知,当集流锥锥角γ由30°增大为40°时,平均单发冲蚀量Δd由0.001 53 mm减小到0.000 79 mm。由此,在式(14)的基础上,提出了集流锥结构坡膛冲蚀经验模型:

(23)

式中:锥角γ影响修正系数c=β/[1+(sinγ)0.14]。由此计算得到,γ=30°时,Δdγ=0.001 59 mm;γ=40°时,Δdγ=0.000 789 mm。计算结果与试验结果吻合非常好,验证了仿真模型的正确性。

4 结束语

本文基于高速动态粒子冲蚀的身管寿命新理论,建立了身管冲蚀计算数学模型,并提出了采用在身管内膛增加集流锥结构的方法来减缓坡膛处火药颗粒的冲蚀效应的设想。针对锥角分别为30°和40°时的两种集流锥结构进行试验验证。结果表明,单发冲蚀量显著减小,使得某155 mm火炮全装药单发冲蚀量由现有水平0.003 1 mm减小为0.000 79 mm,计算结果与试验吻合较好,初步验证了高动态粒子冲蚀理论的有效性和正确性,该理论可以为内膛表面强化处理、微粒子缓蚀等提高身管寿命的技术途径提供指导。