考虑初始变形的煤炭漏斗车车体结构屈曲分析

谢素明,王盛东,李涛,2

(1. 大连交通大学 机车车辆工程学院, 辽宁 大连 116028;2.齐齐哈尔轨道交通装备有限责任公司,黑龙江 齐齐哈尔 161002)

铁路货运漏斗车因其具有周转快、卸货效率高等特点,被广泛用于煤、焦炭、水泥、粮食、石料等散粒货物运输。面对铁路货运高速、重载、轻量化的发展,由薄板组焊而成的漏斗车斜端墙和弧形侧墙结构会承受更大的散粒货物压力和变形,结构失稳问题突出[1]。因此,漏斗车车体设计重点已由结构强度设计转向薄板结构稳定性设计。

目前,在重载货车车体侧压力分布与结构稳定性研究方面,赵俊杰等[2]以旋轮线作为破裂面模型,建立了散粒微层的极限平衡方程,通过数值计算得出了符合铁路货车的散粒货物侧压力公式;赵方伟等[3]采用修正的D-P模型,数值模拟散粒煤的本构模型,研究C80B型敞车的静侧压力分布;冯创友等[4]对K75-ARC型漏斗车的端部侧支撑结构在顶车工况下的稳定性进行了研究,分析变形原因并提出合理的解决方案。

为准确分析散粒煤对车体结构作用引起的结构变形,本文研究散粒货物对车体结构作用的模拟方法——基于AAR标准的压力公式法和基于D-P模型的有限元法;进而以有限元法的车体结构位移为基准,修正漏斗车侧、端墙的压力公式。将散粒煤作用下的结构变形作为漏斗车车体非线性屈曲分析的初始位移,研究车体薄板结构的失稳临界载荷。并针对车体结构的失稳区域,给出提高结构屈曲临界载荷的具体措施。

1 模拟方法

漏斗车车体在车钩纵向压缩载荷作用下进行非线性屈曲分析时,准确地计算出侧、端墙结构在散粒货物作用下产生的变形是保证车体屈曲分析精度的前提。散粒货物对车体结构作用的模拟方法主要有压力公式法和有限元法:前者根据AAR标准中的静水压力公式[5]来模拟散粒货物对车体的作用,建模简单、计算效率高、应用广泛;后者利用实体单元模拟散粒货物,并与车体结构的单元建立接触关系来模拟散粒货物对车体的作用,因离散散粒货物、车体结构以及它们之间接触关系复杂,而且有限元分析涉及非线性计算,工作量大且耗时,所以难以工程应用。

1.1 压力公式法

AAR标准规定:车辆结构设计中,应考虑粒状、块状或粉状货物对车体的压力,即:

(1)

式中:P为单位长度上的压力;w为单位体积货物的重量;h为距压力零点的垂向距离;φ为安息角(货物的自然倾斜角取25°)。

利用式(1)将压力施加于车体结构时,考虑到无盖车辆漏斗车有堆高现象,常选取高于车体顶部304.8 mm的位置作为压力零点。另外,式(1)给出的是单位长度的压力,沿长度L积分可得整个面积上的压力为:

(2)

对式(2)分别沿长度和高度方向求导,得到单位面积上的压力为:

(3)

由式(3)施加散粒煤对车体侧、端墙及底架等区域的压力时,为保证散粒煤总重,还需基于车体有限元分析获得车体不同区域的具体压力数值,详见3.1节。

1.2 有限元法

散粒货物介于固体与液体之间,其受压屈服强度远大于受拉屈服强度,可以采取修正的D-P准则作为描述散粒货物的本构模型。

ANSYS程序中D-P模型的参数为:黏聚力、膨胀角、内摩擦角。散粒煤可被视为理想散体,在压缩状态下会有一定的黏聚力,通过给模型设置较小黏聚力,解决D-P准则在黏聚力为零时出现求解不收敛的问题。散粒煤的内摩擦角反映散粒间摩擦特性和抗剪强度[3]。散粒煤的本构模型参数:弹性模量为3.73×106Pa; 泊松比为0.3; 密度为1×10-9t/mm3;黏聚力为4 MPa;膨胀角为0°;内摩擦角为22°。

利用实体单元模拟散粒煤,常采用solid 45单元,车体结构常离散为shell 181单元。车体底架、端墙和侧墙与散粒煤之间应建立刚柔接触关系,接触类型常选取没有接触表面单元尺寸限制的面面接触。刚度相对较大的车体结构单元表面作为接触主面,散粒煤单元表面作为从面。建立面面接触关系时应保证接触对的法线方向一致。

2 煤炭漏斗车压力公式修正

尽管采用有限元法模拟散粒货物对车体结构的作用更为准确,但当计算边界条件不对称或需要对重车整体车体结构性能进行有限元分析时,模拟散粒货物的单元数量太大,常常无法实现计算。因此,应借助有限元法的结构变形结果修正压力公式(3)。

2.1 分析模型

某煤炭漏斗车的轴重为30 t、自重为23.5 t、总重为120 t、容积为106.6 m3、车辆定距为11.8 m。全钢焊车体主要由底架、侧墙、端墙等组成。底架由牵枕梁、中梁、下侧梁、横梁、脊背及端漏斗板等组成;侧墙采用大圆弧包板式结构,由侧板、隔板和上侧梁等组焊而成;端墙由端板、上端梁、横梁、端柱和斜撑板等组焊而成。其中牵枕梁、中梁、下侧梁采用屈服强度为450 MPa的高强度耐候钢,侧、端墙等与煤接触部位采用屈服强度为350 MPa的不锈钢。

车体结构以任意四节点薄壳单元为主,三节点薄壳单元为辅,1/4车体结构的单元总数为685 076,节点总数为674 357。以四面体单元模拟1/4散粒煤的单元总数为5 090 630,节点总数为1 037 054。1/4重车车体的有限元模型见图1。

图1 1/4重车车体的有限元模型

在散粒煤的作用下对车体结构进行静强度分析时,模型在纵向对称面内约束纵向线位移及绕垂向、横向的转动;在横向对称面内约束横向线位移及绕纵向、垂向的转动;在心盘处约束垂向线位移。

利用压力公式法施加散粒煤对车体的作用时,过程如下:

(1)由车体设计参数确定单位体积货物重量:

(4)

(2)将其代入式(3),得到侧墙面压力为:

(5)

经有限元分析得:侧墙表面承受的散粒煤总压力的垂向分力Fyc=9.651 kN。

(3)货物总重减去Fyc,可得底架和端墙表面承受的散粒煤的总垂向分力Fych=463.699 kN。

(4)假设底架、端墙表面施加的压力公式为:

Fy=Ah

(6)

式中:A为系数。

首先,对底架和端墙施加面压力,Fy=1×h。经计算得:底架和端墙表面承受的散粒煤总压力的垂向分力Fy1=5.542×107kN;再通过Fych与Fy1的比值,求出系数A=8.367×10-6,即端墙和底架面压力为:

Pd=8.367×10-6hN/mm2

(7)

利用式(5)和式(7)施加散粒煤对车体压力之后,仍需依据车体有限元分析的垂向支反力的数据,验证散粒煤重量施加的准确性。

2.2 侧墙压力公式修正

在散粒煤作用下,侧墙的主要位移为横向位移,见图2。由图2可以看出:压力公式法的最大横向位移为5.025 mm,最大位移发生在靠近端墙的侧墙上部区域;有限元法的最大横向位移为3.932 mm,最大位移发生在靠近端墙的侧墙中部区域。

(a)压力公式法

为分析两种方法的侧墙横向位移沿高度的变化规律,选取了5个典型截面(截面I～截面V),这些截面的横向位移沿高度的变化曲线见图3。

(a)截面I

由图3可看出:距离侧墙顶部500～1 500 mm区间,两方法的各截面的横向位移差较大,其中截面V的位移差最大,约为5 mm。将该区域等分为两个区域,500 ～ 1 000 mm为A区,1 000 ～ 1 500 mm为B区。图4为侧墙的截面位置及压力修正区域示意图。

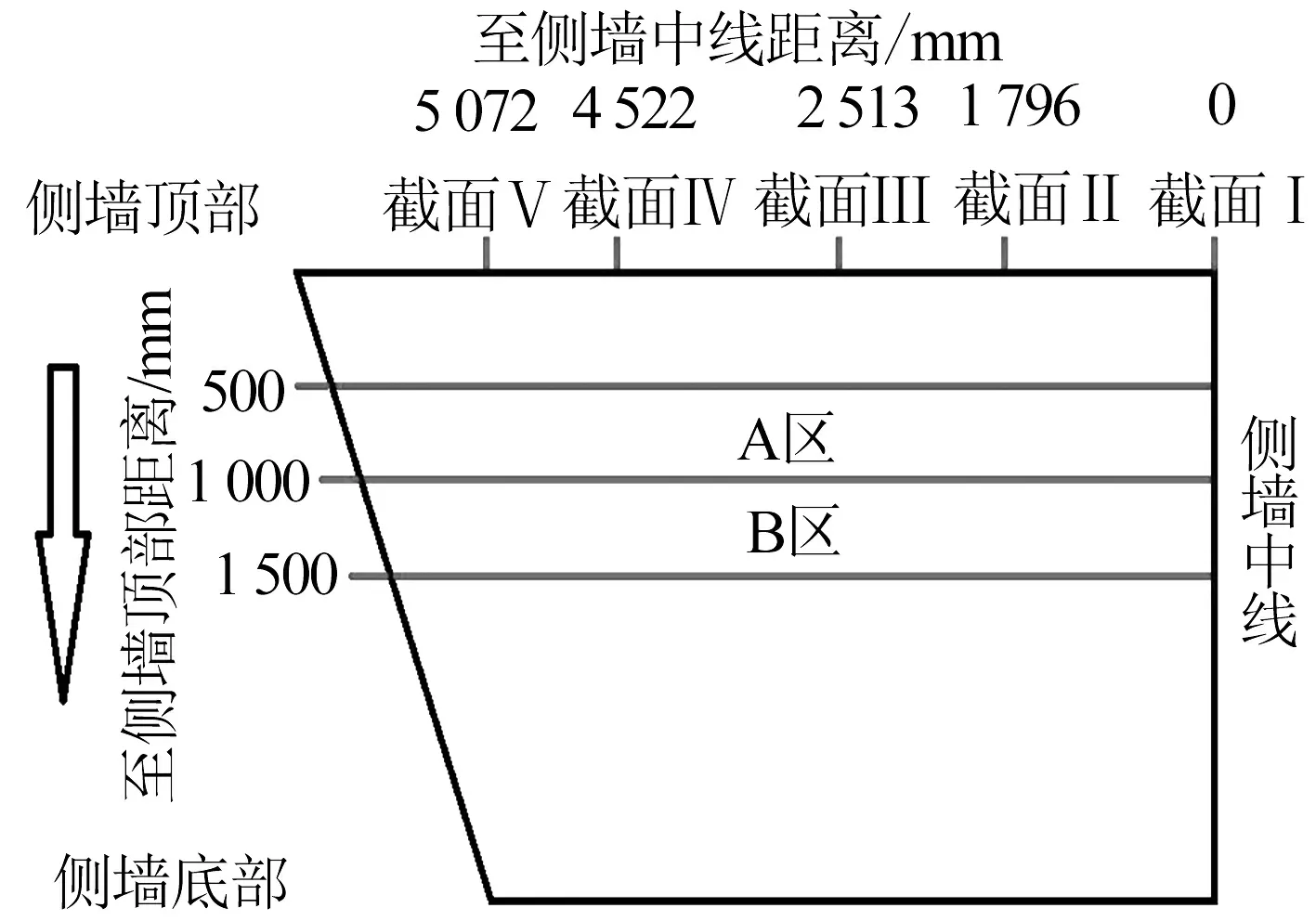
图4 侧墙的截面位置及压力修正区域示意图

以有限元法的位移为基准,修正侧墙横向位移相差较大区域A、B的压力公式(5),使两种方法的侧墙横向位移沿高度变化趋于一致。修正后,侧墙区域A、B的表面压力为PcA=0.901×10-6hN/mm2、PcB=1.802×10-6hN/mm2,压力修正系数分别为0.25和0.5。有限元法与压力修正后的侧墙横向位移的三维图见图5,两者相当接近。

(a)有限元法

2.3 端墙压力公式修正

在散粒煤作用下,端墙的主要位移为纵向位移,见图6。由图6可以看出:压力公式法的端墙最大纵向位移为5.542 mm,最大位移发生在端墙中部靠近侧墙区域;有限元法的端墙最大纵向位移为2.797 mm,最大位移出现在端墙顶部中间区域。

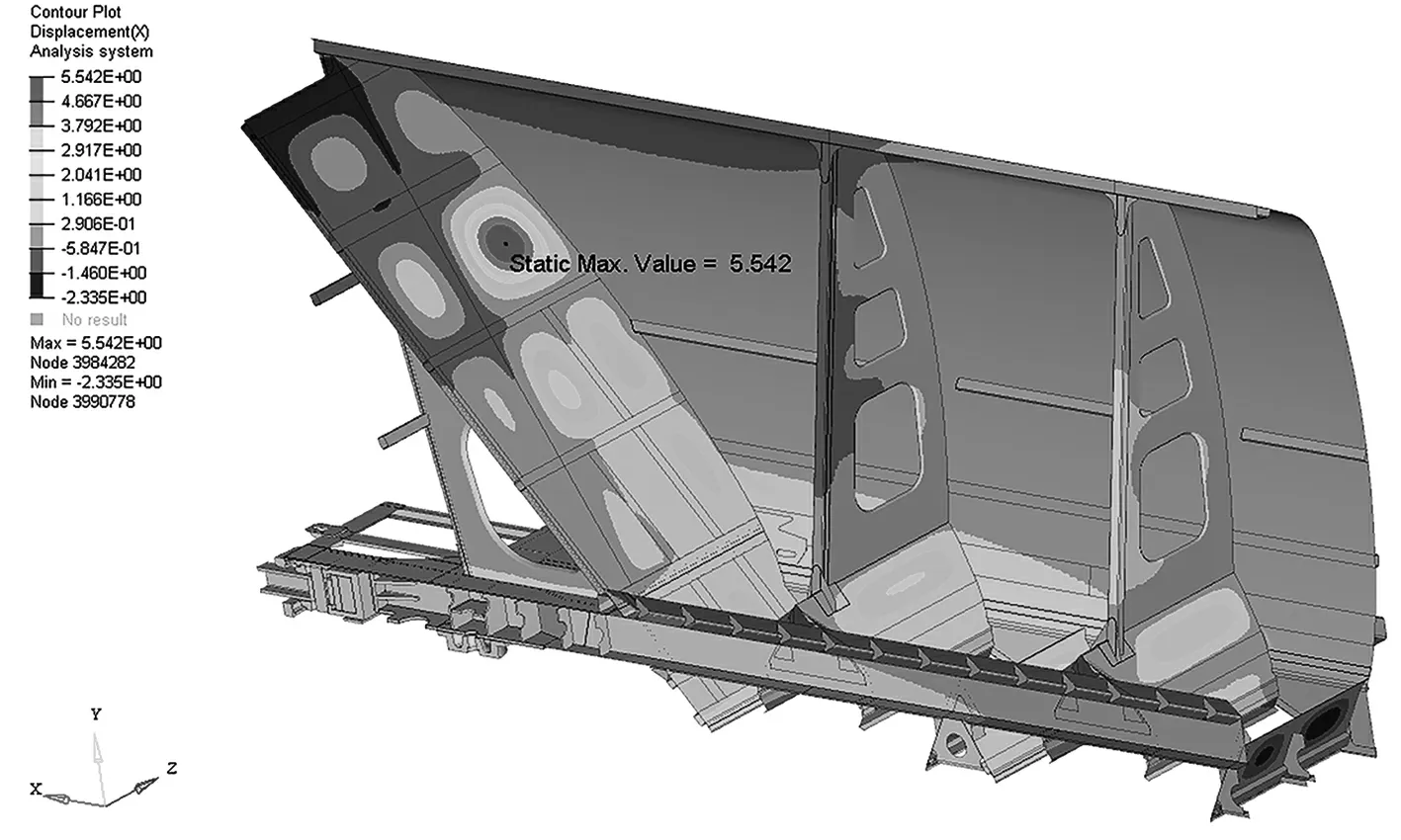
(a)压力公式法

为分析两种方法的端墙纵向位移沿高度的变化规律,选取了6个典型截面(截面I～截面VI),这些截面的纵向位移沿高度的变化曲线见图7。从图7可以看出:截面II、III、IV的位移在高度300～600 mm(视为A区)内最大相差2.2 mm; 截面VI的位移在高度1 000～1 500 mm(视为B区)内最大相差6 mm;截面V的位移在高度2 000～2 500 mm(视为C区)内最大相差2 mm。各截面位置及压力修正区域见图8。

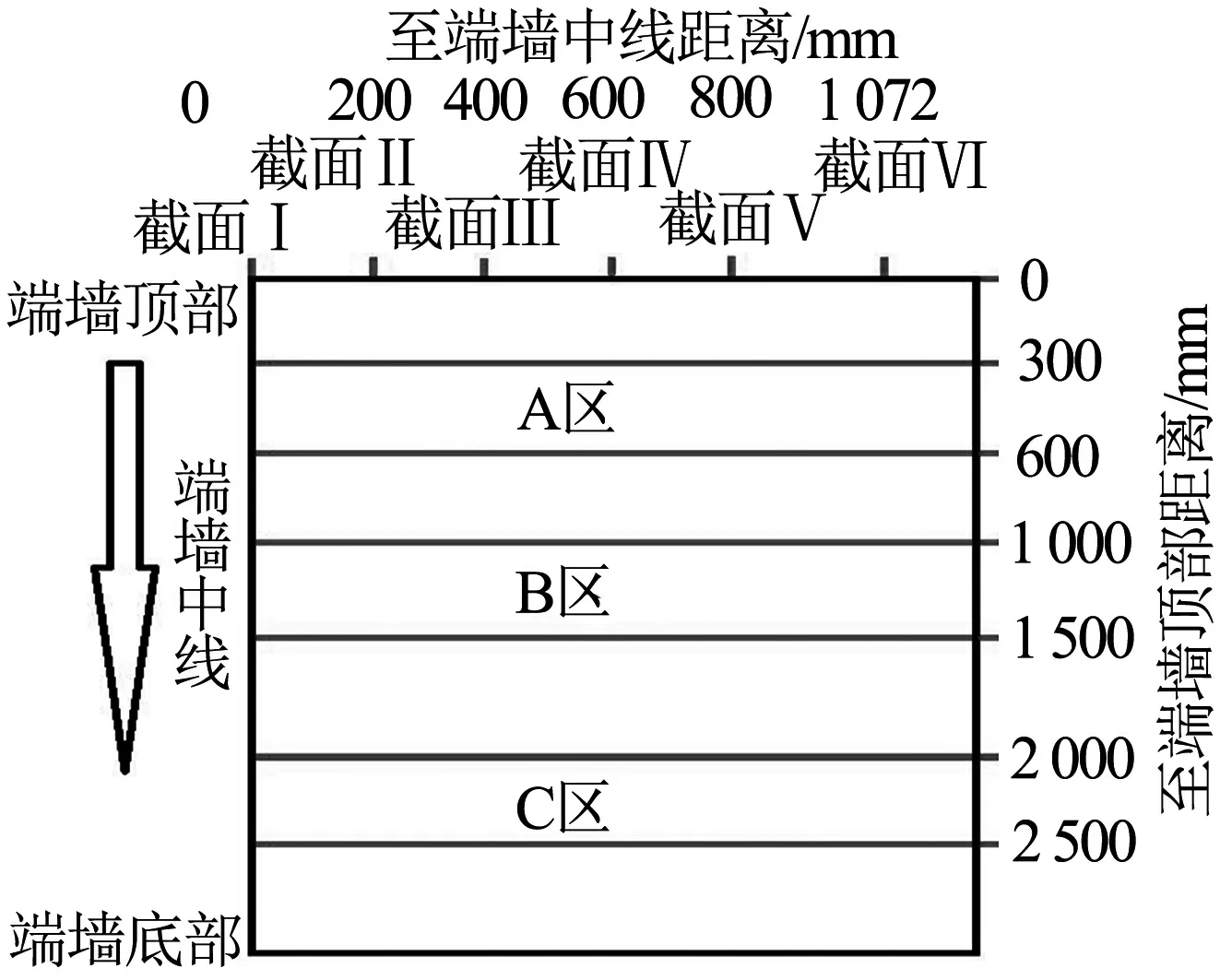
图8 端墙的截面位置及压力修正区域示意图

以有限元法的位移为基准,修正端墙纵向位移相差较大区域A、B、C的压力公式(7),使两种方法的端墙纵向位移沿高度变化趋于一致。修正后,端墙区域A、B、C的表面压力分别为PdA=1.046×10-6hN/mm2、PdB=2.092×10-6hN/mm2、PdC=4.184×10-6hN/mm2,各区域的压力修正系数分别为0.125、0.25、0.5。有限元法与压力修正后的端墙纵向位移的三维图见图9,两者的结果很接近。

(a)有限元法

3 车体结构屈曲分析

基于有限元方法的、写成特征值问题形式的结构非线性屈曲方程为:

[KTn+λΔK]{u}=0

(8)

式中:ΔK=KTnKT(n-1),KTn和KT(n-1)是在屈曲点附近的结点上的切线刚度矩阵。KT为切线刚度矩阵,它与平衡时求得的位移u和载荷参数p有关[6]:

KT(u,p)=K0+KL+K

(9)

式中:K0为小位移刚度矩阵;KL为初位移刚度矩阵;K为初应力刚度矩阵。随着p和u的增大,KT也发生了质的变化。当p达到某个临界值pcr时,u也相应地达到某个临界的平衡位置。λ为pcr与计算载荷的比值,即屈曲因子。

3.1 线性屈曲分析

当忽略初位移影响后,结构线性屈曲方程[7]为:

(K0+λKσ)Δu=0

(10)

通常,结构的线性屈曲临界载荷大于其非线性屈曲临界载荷。前者可用于预测结构失稳的临界上限和失稳部位,也可为结构非线性屈曲分析提供依据[8]。

在纵向压缩载荷4 450 kN作用下,车体侧、端墙结构线性失稳的屈曲振型见图10。由图10可以看出:侧墙失稳部位不是压力调整区域,而是位于侧墙下部,屈曲因子为0.89,临界载荷为3 960.5 kN;端墙失稳部位在端墙B区,屈曲因子为0.52,临界载荷为2 314 kN。

显然,纵向压缩载荷作用时,由薄板结构形成的侧、端墙易发生屈曲失稳。漏斗车车体承受货物载荷作用时,侧、端墙产生的变形将成为结构的初始缺陷,会使车体部件结构的屈曲临界载荷降低。所以,还需要对车体进行非线性屈曲分析。

3.2 非线性屈曲分析

将重车车体侧、端墙的变形作为非线性屈曲分析的初始缺陷(见图5和图9),同时,为保证迭代过程中车体结构发生屈曲失稳,将侧、端墙线性屈曲分析的最大临界载荷增大15%(即4 554.7 kN),作为纵向压缩载荷施加在车体车钩处。

车体侧、端墙失稳部位的载荷与位移的关系曲线见图11,图中曲线拐点对应的载荷即为临界载荷。由于修正前后压力公式得到的侧墙失稳区域的位移相近,故两者在该区域的临界载荷均为3 550 kN(图11(a)),比线性屈曲分析的临界载荷减小10.4%;应用修正前压力公式的端墙屈曲临界载荷为1 780 kN,比线性屈曲分析的降低了23.1%。应用修正后压力公式的端墙屈曲临界载荷提高至2 045 kN,较应用修正前压力公式的值增大了14.9%。原因是修正前压力公式得到的端墙失稳区域的位移大于由修正后压力公式得到的位移,也就是说屈曲分析时前者的初始缺陷大于后者的。

3.3 提高屈曲临界载荷的具体措施

由上述分析可知:车体侧、端墙结构的线性和非线性屈曲的临界载荷均小于车体设计的纵向压缩载荷(4 450 kN),显然不满足设计要求。考虑到由散粒煤引起侧、端墙的变形实际上已成为结构的初始缺陷,并降低了车体部件结构的屈曲临界载荷。据此,可分别通过提高侧墙与端墙失稳部位的横向刚度和纵向刚度,减少结构的初始变形,进而提高结构的屈曲临界载荷。

为加强侧墙失稳部位抵抗横向变形的能力,增加一个槽型梁结构(图12(a)),梁厚度为4 mm,尺寸为2 200 mm×40 mm×30 mm;为增加端墙失稳部位的纵向刚度,端墙增加6个槽型梁结构(图12(b)),梁厚度为3.5 mm,尺寸为800 mm×70 mm×50 mm。

(a)侧墙

车体侧、端墙局部结构补强后,经屈曲分析:侧墙线性屈曲因子为1.03,端墙线性屈曲因子为1.01,均大于补强前的屈曲因子。应用修正后压力公式的侧墙屈曲临界载荷为4 092 kN,端墙屈曲临界载荷为3 164 kN,均大于补强前的临界载荷。

4 结论

(1)经分析压力公式法与有限元法的侧、端墙位移结果,侧墙的A和B区内横向位移差值均为5 mm;端墙的A、B、C区内纵向位移差分别为2.2、6、2 mm。

(2)基于有限元法模拟散粒煤对车体作用的变形结果, 得到了侧墙A和B区的压力修正系数分别为0.25、0.5;端墙A、B、C区的压力修正系数分别为0.125、0.25、0.5。

(3)侧墙的最小线性屈曲因子为0.89,失稳部位在侧墙下部,临界载荷为3 960.5 kN;端墙的最小线性屈曲因子为0.52,失稳部位在端墙B区,临界载荷为2 314 kN。

(4)以修正前后的压力公式施加散粒煤对车体的作用产生的结构变形,作为车体非线性屈曲分析的初始缺陷,结果表明:压力修正前、后的侧墙临界载荷均为3 550 kN,比线性屈曲的降低了10.4%;压力修正前的端墙临界载荷为1 780 kN,较线性屈曲的降低了23.1%,压力修正后的临界载荷增大了14.9%。

(5)通过提高侧墙与端墙失稳部位的横向刚度和纵向刚度的改进设计,可使侧、端墙的线性屈曲因子分别提升至1.03、1.01;应用修正后压力公式的侧、端墙临界载荷提升至4 092、3 164 kN。