面向高速公路流量预测的自适应图注意力网络

袁毅,王振华,滕志伟,黄文军,王然,余梁

(1.安徽毫阜高速公路有限公司,安徽 毫州 236000;2.招商新智科技有限公司,北京 100000;3.北京交通大学 计算机与信息技术学院,北京 100044)

高速公路流量不仅可以反映道路的交通运行状况,还可以辅助分析道路发生事故的情况,是进行交通管理规划以及相关交通设施建设部署的重要参考。交通流量具有时间相关性和空间相关性[1-3],根据研究对象为单一指定检测点处的流量还是路网系统对指定检测点流量的影响,可将流量研究分为基于时间相关性和时空相关性两类。时间序列模型主要分析流量历史数据在时间尺度上的变化规律[4-5]。由于多个检测点处的流量存在相互影响,因此利用好不同位置流量间的空间相关性,将有利于实现更准确的交通流预测[6-8]。

交通流数据中存在着动态的时空相关性,传统方法难以同时考虑多种影响因素,而基于图卷积神经网络的深度学习方法[9-13]可设计更精细的特征提取方法,建模交通数据中的时空相关性。图卷积神经网络使用共享的参数空间,学习不同检测点处交通数据的空间相关性,当不同检测点流量变化相似时,这种方法比较有效[14-15]。但通过实例验证分析发现,邻接检测点处流量的峰值和变化趋势差别较大,使用共享参数空间的图卷积难以学习到各个检测点处流量特定的变化模式。因此,采用矩阵分解的方法构建节点自适应参数学习模块,根据节点的嵌入表示,从多种候选模式的集合中学习其特定的变化模式[16]。此外,基于图卷积网络的方法需要根据距离预先定义邻接关系图来捕获空间相关性,由于先验知识有限,预定义图中具有邻接关系的节点在流量变化规律上没有明显的相关性[17],为此,本文通过生成自适应邻接矩阵以更全面地捕获交通数据的空间相关性。

本文提出一种面向高速公路流量预测的自适应图注意力网络(Adaptive Graph Attention Net-work,AGAT)模型,该模型将节点自适应参数学习模块、自适应邻接矩阵生成模块和门控循环单元整合,以捕获交通数据中复杂的时空相关性。但是,循环神经网络难以捕获长程的时间相关性[18],并且会带来一定的信息损失[19],为此,本文设计了一个转换注意力层,直接建模未来时间步信息与历史多个时间步信息的相关性,从而实现准确的交通流量预测。

1 流量数据特性分析

本节分析桂林市高速路网中4个断面(节点)在相同时间片段流量的时空特性。 选取2022年2月8日0时到2月12日0时共4天的流量序列数据进行可视化,流量数据采样粒度为1次/h。断面流量变化趋势见图1,其中图1(a)～图1(c)3个断面在邻接图中具有邻接关系,图1(d)与以上3个断面都没有邻接关系。由图1可知,车辆流量的分布呈现明显的周期性。另外,虽然3个具有邻接关系的断面流量分布的整体趋势相近,但在平均值与峰值水平上三者相差较大。在以往的研究中,选取的研究对象通常是普通的城区道路,采样点密度大,并且采样点之间的距离短,所以相邻的节点流量数值相近,变化平缓;但本文选取的高速公路断面总是伴随互通与收费站而出现, 采样点之间的距离相隔较远且很稀疏,流量变化与节点所处地段、所在地天气更加相关。

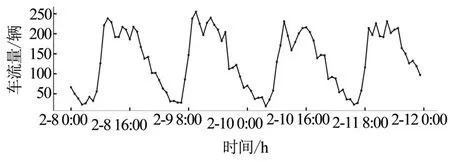
(a) 灵川1-桂林招商公路1

与城市路网相比,高速公路网因为存在许多长途车辆,图上距离相隔较远的两个节点也更可能表现出较强的相关性,如图1(b)与图1(d)所示,断面虽没有邻接关系,但都在同一方向的高速公路上,其流量变化也呈现相似的趋势。因此,由于先验知识有限,根据相似度或距离预先定义邻接关系图难以捕获节点间的空间相关性。另外,通过分析可以发现,对于同一个断面,其流量在各天中的分布具有相似性。图2展示了灵川1-桂林招商公路1断面从2022年2月7日到2月28日共22天的流量变化情况。

图2 断面流量长时变化趋势

本文使用节点自适应参数学习模块来捕获各个节点特定的交通量变化模式,基于自适应邻接矩阵学习路网数据中潜在的空间相关性,将其与门控循环神经网络整合成自适应图卷积循环神经网络,学习流量序列中的时空相关性,并通过注意力机制建模未来时间和历史图信号矩阵的相关性,预测未来的流量值。

2 自适应图注意力网络

本文提出面向高速公路流量预测的自适应图注意力网络,见图3。通过自适应图卷积循环神经网络学习流量数据中的时空相关性,并设计了一个转换注意力层, 建模历史交通数据与未来交通数据的相关性,以解决循环神经网络难以捕获长期的时间相关性和产生信息损失的问题。

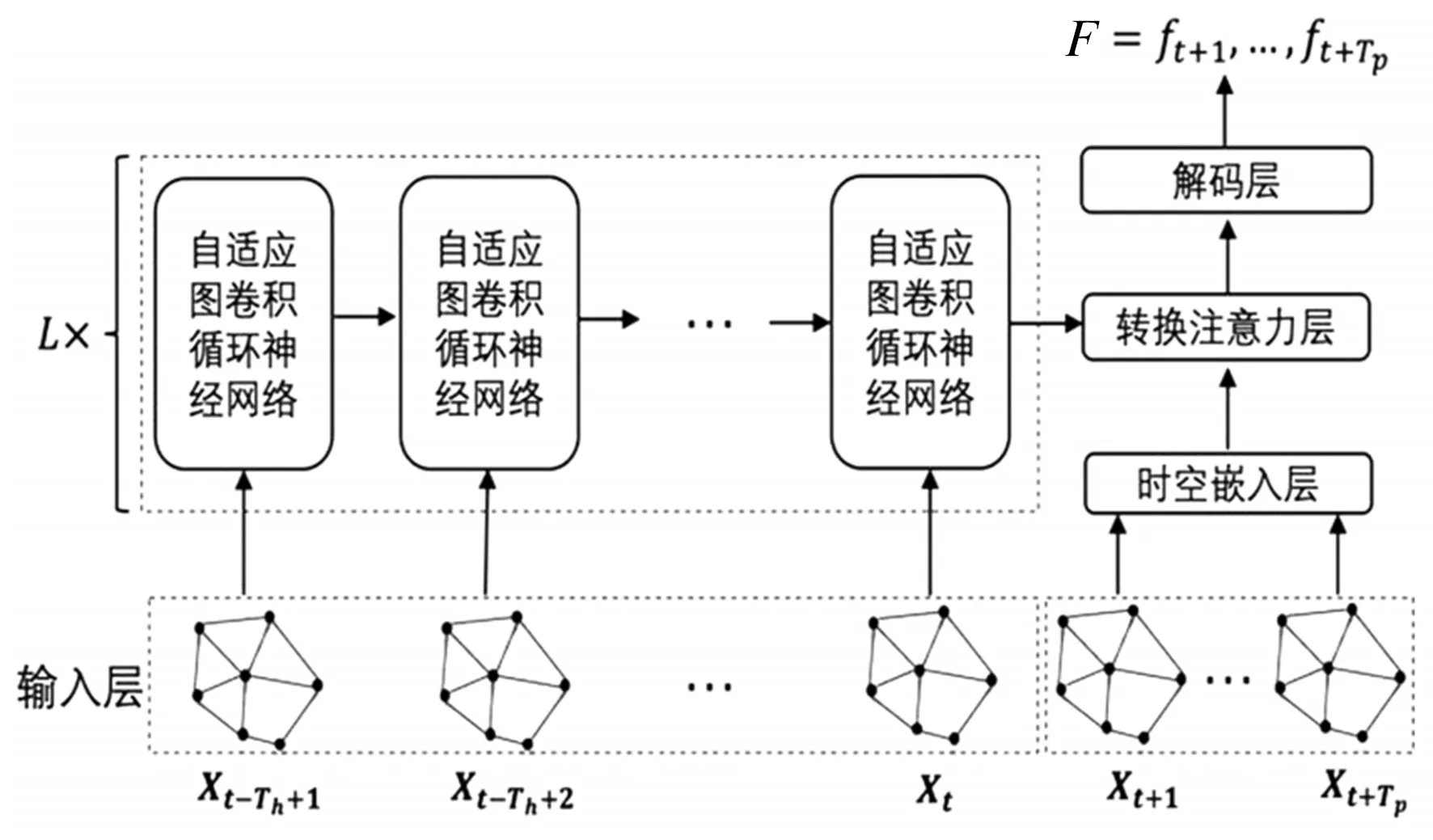
图3 面向高速公路流量预测的自适应图注意力网络

2.1 输入层

经过数据预处理得到路网G中所有节点在各个时间步的特征,以该特征作为输入。具体输入特征构造方式如下:在第t个时间间隔内,观测到高速公路路网G上的信号,用矩阵Xt=(xt,1,xt,2,…,xt,N)T∈N×C表示,式中1×C表示第t个时间间隔内节点v的C个观测量的取值。其中为该时间间隔内节点上游路段车速,为该时间间隔内节点下游路段车速,为该时间间隔内节点流量值,为该时间段内节点处平均气温,为该时间段内节点处平均降水量,为该时间段内节点处可见度,为该时间段对应的周中天数,为该时间段对应的时间片段。

2.2 节点自适应参数学习模块

图卷积网络(Graph Convolutional Network, GCN)是一种用于处理非欧式结构数据的神经网络。现实中的高速公路路网是不规则的,可看作非欧式结构,可以使用图卷积网络来处理高速公路路网数据,以捕获不同位置流量数据的空间相关性,提升交通数据预测的精度。图卷积运算可用一阶切比雪夫多项式展开逼近,并且可以推广到高维图卷积:

(1)

式中:IN为维度是N×N的单位矩阵;A∈N×N为图G的邻接矩阵;D为度矩阵;Xt∈N×C和Zt∈N×F分别为第t个时间间隔内图卷积网络的输入和输出;Θ∈C×F和b∈N×1分别为可学习权重和偏置项。图卷积运算可以看作是利用所有节点共享的Θ和b,将节点特征xt,i∈R1×C转化为zt,i∈R1×F。虽然在一些情况下,参数共享对学习邻近节点间的空间相关性和主导的流量变化模式是有效的,但是,由流量时空分布特性可知,相邻节点在一些时间段的流量变化模式是不相似的,这是因为节点的流量变化还受到其他因素比如可见度、降水量等的影响。由于流量序列的动态性,不同位置的流量序列变化具有多种模式。因此,通过共享参数的方式学习邻近节点间的空间相关性和流量的主导变化模式,不足以实现准确的流量预测,需要对每个节点维持特定的参数空间以学习节点特有的模式。但是,对每个节点分配参数空间将得到Θ∈N×C×F,当N较大时,难以对其进行优化,并且可能导致过拟合问题。为解决该问题,可以基于矩阵分解方法学习两个较小的参数矩阵:①节点嵌入矩阵Eg∈N×d,其中d为嵌入维度且d≪N;②权重池Wg∈d×C×F。Θ可由两个参数矩阵生成,即Θ=Eg·Wg,该等式可解释为对节点i,通过其节点嵌入表示与权重池Wg中对应的可学习参数相乘得到Θi,以表示节点i特定的变化模式。最后,以第t个时间间隔内的输入为例,基于节点自适应参数学习的图卷积网络可定义为:

(2)

2.3 自适应邻接矩阵生成模块

图卷积运算需要预先定义邻接矩阵,很多现有工作利用距离函数或相似度函数提前计算好图的邻接矩阵[20-21]。但是,这种预先定义邻接矩阵的方式不能涵盖关于空间相关性的完整信息,因此在预测任务中可能产生较大偏差。为解决该问题,本文生成自适应邻接矩阵以学习路网数据中的潜在空间相关性。该方法首先为所有节点初始化一个可学习的节点嵌入字典EA∈N×de,EA中的每一行表示一个节点的嵌入表示,de为嵌入表示的维度。可通过EA和的乘积计算节点之间的空间相关性。为减少训练过程中的重复计算,可以基于EA和的乘积直接生成并通过SoftMax标准化自适应邻接矩阵。自适应邻接矩阵的生成不需要任何先验知识,在训练过程中通过梯度下降更新节点嵌入矩阵EA的参数,以实现自适应地发现节点间潜在的空间相关性。基于自适应邻接矩阵生成的图卷积计算可定义为:

(3)

2.4 自适应图卷积循环神经网络

为实现准确的流量预测,除了挖掘不同位置交通数据的空间相关性之外,还需要了解交通数据中的时间相关性。因此,本文将节点自适应参数学习模块和自适应邻接矩阵生成模块整合到门控循环单元中,以捕获数据中的时空相关性。基于自适应邻接矩阵生成模块建模节点间的空间相关性:

(4)

为学习节点独有的模式,利用节点自适应参数学习模块替换门控循环单元中的多层感知器。整合后的自适应图卷积循环神经网络定义为:

(5)

(6)

(7)

(8)

通过堆叠多个自适应图卷积循环神经网络作为编码器学习节点特有的流量变化模式和复杂的时空相关性,以实现准确的流量预测。

2.5 转换注意力层

本文基于注意力机制[22]设计了一个转换注意力层,建模历史信息与未来时间步信息的相关性,以减轻循环神经网络产生的信息损失和误差传播。

首先通过时空嵌入层得到各个时间步的节点嵌入表示。为融合节点的空间信息,使用上一节中的节点嵌入矩阵EA,其中ev∈d为EA的第v行。为了获得节点在不同时间步的相关性,将节点嵌入表示与时间步对应的一天内的小时数拼接,作为新的节点嵌入表示。对于节点v(v=1,…,N),其在历史数据步Th和未来预测时间步Tp的时间片段的嵌入表示为ek,v∈d+1,其中k=t-Th+1,t-Th+2,…,t+Tp,ek,v=‖{ev,mod (k,24)}∈d+1。

转换注意力层建模每一个未来时间步和历史Th个时间步信息的相关性。对于节点v,预测时间步pj(pj=t+1,t+2,…,t+Tp)与历史时间步q(q=t-Th+1,t-Th,…,t)的注意力权重的计算为:

(9)

(10)

通过转换注意力层计算得到:

(11)

解码器由k个全连接层构成,对转换注意力层得到的预测步的节点嵌入表示解码,得到预测时间步各个节点处的流量F=(ft+1,ft+2,…,ft+Tp)。

2.6 模型训练

模型训练的损失函数使用均方误差函数,优化算法选用Adam算法[23],Adam算法是一种基于“动量”思想的随机梯度下降算法,在迭代前计算梯度的两阶动量并计算滑动平均值,并用于更新参数。

3 试验与结果

本文采用桂林市路网区域的交通数据,时间跨度从2022年1月1日到2月28日共59天,36个节点,以1 h为单位聚合每个断面的流量。按照6∶2∶2的比例划分训练集、验证集和测试集,使用训练集的均值和标准差对所有数据进行归一化,输入Th=8个时间步的数据,预测Tp=1个时间步的交通流量。

3.1 评价指标

选取平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Squared Error,RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error, MAPE),对本文提出模型的预测性能进行验证。

3.2 基线模型

选取以下基线模型与本文提出的模型进行对比:①HA:对每一个节点都以输入数据所有时间步上的平均值作为下一时间步的预测值;②GCN[24]:用谱域中对角化的线性算子替代经典卷积算子实现卷积操作;③RNN[25]:能很好地挖掘数据中的时序信息与语义信息,这里使用门控循环单元(GRU)作为编码器和解码器;④GMAN[9]:借助自注意力机制实现了空间与时间维度的注意力模块,多个时空注意力模块堆叠组成编码器与解码器;⑤AGCRN[16]:使用数据自适应图和自适应图卷积循环神经网络模块,为每个节点都学习了一个特定的参数空间,挖掘流量序列中不同的模式。

3.3 参数设置

模型自适应图卷积模块的嵌入维度设置为24,堆叠的自适应图卷积模块数量设置为1,循环神经网络单元隐藏状态的维度设置为64,转换注意力层的注意力头数设置为4,解码器中的全连接层数为1,训练时小批量大小设置为8,初始学习率设置为0.003,每10步衰减30%,早停步数设置为15。

3.4 试验结果分析

使用不同方法在相同场景下进行预测,试验结果见表1。

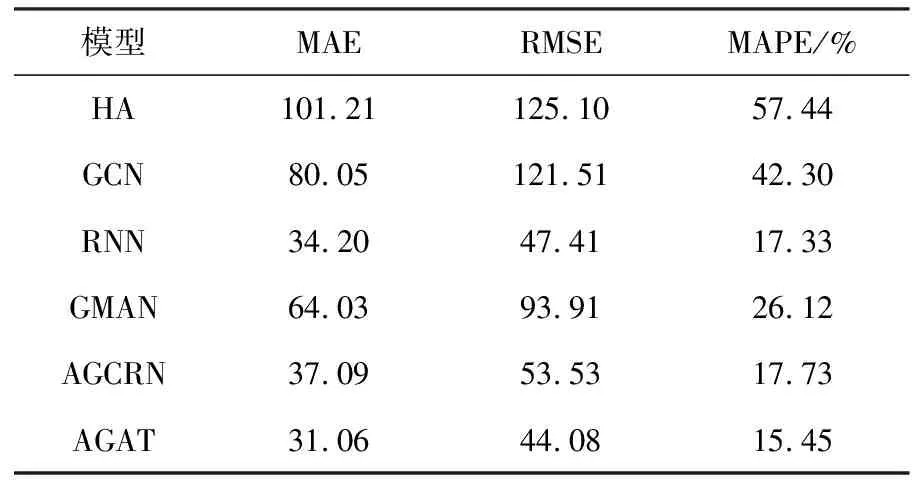
表1 不同方法在数据集上的试验结果比较

评价指标MAE、RMSE、MAPE越低,模型预测越准确。从表1中看出,除HA外,仅利用图邻接关系的GCN表现最差,GMAN次之。RNN虽然仅关注数据中的时序信息,但在本次试验中表现出色,而同样使用了自适应图卷积的AGCRN表现不佳,可能是因为AGCRN使用一维卷积来解码循环模块编码得到的表示,不足以解析出编码的所有信息。本文的模型一方面通过节点自适应参数学习模块很好地解决了节点间空间关联度不显著的问题,另一方面使用转换注意力层聚合自适应图卷积模块编码的信息,在最优的基线模型基础上,MAE指标提升了9.2%,RMSE指标提升了7.0%,MAPE指标提升了10.8%。

为了更全面地分析本文模型的优势,对各模型在临桂六塘2-马面立交1断面从2月24日23∶00到2月25日23∶00时间区段的流量预测值进行可视化,流量预测见图4。从图4可以看出,各个基线模型基本保持了和真实值相似的变化趋势,但在数值水平上相差较大。其中AGCRN在识别时间维度上流量变化的能力不如RNN与AGAT,也辅证了AGCRN的卷积解码器未能完全解码出编码后的所有信息的分析。从图中还能看出,AGAT在预测精度上优于其他基线模型。

(a) HA

3.5 消融试验分析

为进一步分析模型各个组件的作用,本文对原模型AGAT的3个变体进行消融试验,将这3个变体与AGAT进行比较,变体的描述如下:

AGAT_wo_NAPL:在AGAT基础上,使用标准图卷积中的权重矩阵代替节点自适应参数学习模块(NAPL)。

AGAT_wo_DAGG:在AGAT基础上,使用标准图卷积中的归一化图邻接矩阵代替自适应邻接矩阵生成模块(DAGG)。

AGAT_wo_TA:在AGAT基础上,使用一维卷积作为解码器来代替转换注意力层(TA)。

消融试验的结果见表2。从表中可知,在不对节点进行自适应参数学习的情况下(AGAT_wo_NAPL),试验效果有明显下降,这意味着节点自适应参数学习模块很好地捕获到了各个节点特定的交通模式。在不使用自适应邻接矩阵生成模块的情况下(AGAT_wo_DAGG),试验效果略有下降,这也说明DAGG模块有比邻接矩阵更优秀的捕获路网数据中潜在的空间相关性的能力,但由于下降效果不显著,稀疏的高速公路路网的空间关联性对流量预测准确性的影响有限。在不使用转换注意力层的情况下(AGAT_wo_TA),试验效果显著下降,说明通过注意力机制直接建模与历史多个时间步的相关性,有效减少了循环神经网络传递信息的损失,转换注意力层有助于模型更准确地预测车流量。

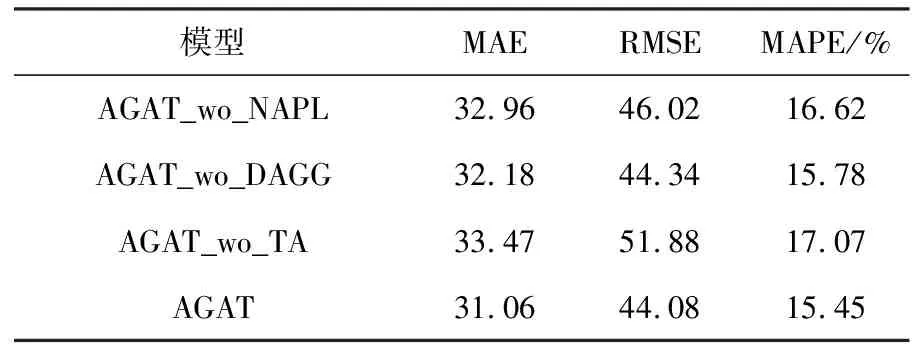
表2 消融试验结果

4 结论

本文通过分析高速公路流量数据的时空分布,针对其分布特性提出了一种面向高速公路流量预测的自适应图注意力网络模型,该模型基于自适应图卷积循环神经网络捕获路网数据中复杂的时空相关性,通过转换注意力层解决循环神经网络难以捕获长期的时间相关性和产生信息损失的问题。将本模型同其他常用的预测方法在相同数据集和相同预测场景下进行试验对比,试验结果表明本模型在预测效果上达到了最优,消融试验也说明了该方法的有效性。但是,本文的方法还有一些优化空间,比如可以考虑其他外部因素,例如节假日等,合理地量化这些因素,更准确地实现流量预测,可作为今后模型优化的方向。