基于网络核密度估计的交通事故黑点识别

罗叶,祁首铭,2,张希,廉冠,杨海华

(1.深圳市城市公共安全技术研究院有限公司,广东 深圳 518000; 2.哈尔滨工业大学 土木与环境学院,广东 深圳 518055; 3.桂林电子科技大学 建筑与交通工程学院,广西 桂林 541004;4.中国建设基础设施有限公司,北京 100029)

道路交通事故造成的伤害是全球严重的公共卫生和社会安全问题。根据世界卫生组织(WHO)的数据[1],全球每年约135万人死于道路交通事故。目前,道路交通事故伤亡人数在全球所有死因中排名第8,预计到2030年将升至第7位。作为全球最大的发展中国家,中国同样面临着交通事故伤害问题,在部分省市,交通事故已经成为导致意外死亡的主要原因[2]。随着城市化进程的不断发展,城市机动化的发展水平已经成为衡量一个国家城市化水平高低的重要指标,然而不断增长的机动车及人口密度给道路交通安全带来巨大压力,在社会资源有限的前提下如何有效降低交通事故率成为难题。自20世纪50年代,英美等发达国家开始对事故多发点进行鉴别及治理以来,交通事故状况得到明显好转。欧盟道路交通事故委员会在对TEN-T公路进行事故多发点治理后,该公路的事故率降低了11%[3]。因此,在追求城市发展的同时准确、高效地采取针对性措施进行事故预防,提高城市道路交通安全水平成为全社会迫切的愿望。

在空间中,大多数情况下交通事故并非随机分布,而是在空间中形成集群[4],从而成为事故黑点(Black Spot),识别交通事故黑点被学者们认为是交通安全改善策略中的第一个关键步骤[5]。常见的事故黑点识别方法主要是基于事故数以及事故率进行鉴别,主要包括事故频数法、当量事故数法、累计频率曲线法、回归分析法、事故率法、当量事故数-事故率法[6]等。这些方法的研究思路为:划分目标路段的固定单元,选取一定范围内的事故数或事故率作为阈值完成事故黑点鉴别,常用于单一路段的事故黑点识别,但结果展现的可视化效果不佳。随着地理信息技术的发展,越来越多的学者将可视化效果更佳的空间分析技术应用于事故黑点识别,Anderson[7]采用平面核密度分析和K均值聚类算法对伦敦城市道路交通事故黑点进行识别;郭璘等[8]采用基于改进的K-means算法对宁波市的交通事故进行分析;黄钢等[9]采用基于改进密度的DBSCAN算法对事故地点与原因进行密度聚类;曹倩等[10]采用事故密度峰值聚类方法,评估风险异质性的道路网交通事故风险。然而,由于交通事故的发生并不存在于二维空间,受到道路网络的约束,Okabe等[11]提出一种基于网络空间约束的核密度方法,并开发出基于Arcmap的插件SANET。此后,由于无须假设先验参数、可视化效果佳、符合道路网空间的实际情况,网络核密度估计算法被应用于交通事故黑点识别、网约车上下客热点识别、犯罪行为热点识别等多个领域[12-16]。目前通常采用经验取值法、自然分段法等对应用网络核密度估计后的事故进行热点识别,但这类方法识别事故黑点不具备统计学意义,因而,该方法在交通事故黑点中的应用仍然不足。

因此,本文在使用网络核密度估计的基础上,结合局部空间自相关分析,鉴别城市道路事故多发点。可在统计学意义上提升事故黑点识别的准确率及效率。

1 研究区域及数据处理

1.1 研究区域及数据概况

本文选取深圳市龙华区作为研究区域,下辖6个街道,共50个社区。本研究所使用的数据包括交通事故数据及道路网络数据。交通事故数据为2018—2020年间3年的交通事故记录,共计1 105例。每条事故记录包括描述性事故地点、事故时间、事故类型、事故基本经过、事故伤亡情况等。道路网络数据来自OpenStreetMap(OSM)2021年的矢量路网数据。

1.2 地理信息匹配

由于原始交通事故数据对应的事故位置信息是描述性信息,因此需要将描述性位置信息进辖6个街道,共50个社区。本研究所使用的数据包括交通事故数据及道路网络数据。交通事故数据为2018—2020年间3年的交通事故记录,共计1 105例。每条事故记录包括描述性事故地点、事故时间、事故类型、事故行地理编码,即将文字位置信息转化为经纬度数据。目前国内常用的在线地理编码服务主要有4种:百度、高德、搜狗及腾讯。根据学者的研究对比,腾讯地图在数据质量以及完备的地址数据方面表现较为优异,高德地图则在地址匹配度方面表现良好[17],因此本文选择腾讯地图以及高德地图作为地理编码的主要工具。

本文调用腾讯地图geocoder API地理编码服务,返回数据包括经纬度信息及地址可信度(reliability)。根据腾讯地图位置服务的官方说明[18],可信度取值范围为1～10级,当该值大于等于7时,解析结果较为准确。因此,本文提取返回结果可信度大于等于7的经纬度值,其余结果通过调用高德地图geocode API实行地址位置解析,最终返回结果显示,仅1.9%的地址未匹配,采用人工纠偏的方式进行位置解析。为便于分析,本文采用的道路网数据为矢量线性数据,无宽度属性,地理编码返回的坐标位置分布在道路两侧,因此通过将数据点投影至最近路网的方式进行道路匹配。此外,高德及腾讯地图返回的经纬度信息均为GCJ02坐标系,为与道路网进行地图匹配,本文将所有返回的经纬度信息转换为WGS84大地坐标系。

本文将2018—2020年3年的1 105例道路交通事故绘制成地理信息散点图,见图1。通过统计每个街道事故数(图2),可以发现,事故主要集中在龙华中心区的龙华街道,其次是大浪街道。

2 事故黑点识别方法研究

2.1 交通事故网络核密度估计模型构建

核密度估计(Kernel Density Estimate, KDE)是一种常用于从事件样本中估计空间过程的强度函数,它属于点模式分析中的非参数方法之一。具体来说,它通过采用平滑的峰值函数(核)对观察到的数据点进行拟合,从而对真实的概率分布曲线进行模拟,展现出平滑的可视化效果,体现出分析目标在空间上的聚集情况,因而被广泛应用于犯罪分布、事故空间分布点事件的热点识别。

平面核密度估计的表达式为:

(1)

式中:λ(s)为事故点s的密度;r为核密度估计的搜索半径(带宽),只有在距离点s半径r范围内的点才能用于估算λ(s);k为点i权重,其大小取决于点i与点s之间的距离dis与搜索半径r的比率。在核密度估计中充分考虑了到中心位置s的距离衰减效应,即到事故点s的距离越长,该点的权值就越低,超出搜索半径距离之外的极限密度为0。因此事故点s的最终密度是通过将搜索半径内所有的点比率相加而得。

平面核密度估计在分析及确定交通事故热点时并不适用。经典的核密度估计是基于一个无限、齐次的二维(2D)空间假定,因此核密度估计采用了事件点之间的欧几里得距离。事实上,交通事故通常发生在道路网络范围内,在道路网络中,车辆的移动总是受到道路网络的约束,在交叉口可能会改变方向,Steenberghen等[19]将网络空间称为1.5D空间。此外,道路网络中点的距离总会大于或等于欧几里得距离,因此在交通事故密度分析中使用平面核密度估计会低估道路网络中交通事故点之间的实际距离,从而会过度识别热点,见图3。

(a) 基于欧式距离的核密度搜索方式

网络核密度估计(Network Kernel Density Estimate, NKDE)是平面核密度估计的扩展形式,两者之间最大的不同在于距离计算方式的差异,相较于计算2D空间均匀区域单元上点事件的密度,网络核密度计算的是道路网络上线性单元(路段)最短路径距离的点事件密度。其计算公式与平面核密度估计类似:

(2)

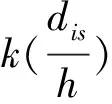
(3)

为确定最优带宽,可根据积分均方差达到最小原则,得到最优带宽计算公式[14]:

(4)

式中:hopt为最优带宽;σ为高斯核函数的标准差;在道路网条件下的σ为事故点数据的网络距离标准差;n为事故点的数量。

2.2 基于网络核密度的局部自相关分析

在道路网的承载下,各路段间具有一定的空间相关关系,若将事故密度定义为风险的量化指标,那么路段之间事故密度的相关关系可以解释为交通事故的风险扩散性[21]。因此可通过计算路段之间事故密度的空间相关关系,从而在统计学意义上识别事故高风险路段。

空间自相关分析中,莫兰指数(Moran′sI)是一种最常用的空间自相关统计方法,也叫聚类和异常值分析法,其通过计算同一分布区域内的相邻空间数据间潜在的依赖性,检测出空间范围内是否存在聚集特性。空间自相关分析大致分为全域法及局域法,其中全域法用于判断空间中是否存在聚集特性,而局域法则侧重于检定某个聚类单元相对研究空间而言是否足够显著。因而局部空间自相关更适用于检测高密度路段的离散情况,在考虑相邻路段的基础上,识别事故多发路段。

局部莫兰指数(Local Moran′sI)的计算方法如下[22]:

(5)

式中:Ii代表第i个路段的Local Moran′sI;xj和xi分别为路段j和路段i的网络核密度值;wij为路段i与路段j在特定领域定义下的空间权重;n为路段总数。Local Moran′sI的值本质上类似于相关性系数(Pearson),其代表了观测值自身与空间滞后Lisa值之间的相关性。当Moran′sI在置信区间内显著,且当观测值与空间滞后值符号相同时,称其为高-高值、低-低值聚类;当观测值与空间滞后值相反时,称其为高-低值或低-高值聚类。

3 实证分析

3.1 事故黑点网络分析

本文采用R语言中spNetwork包[23]中的nkde函数对事故点进行网络核密度分析,并通过tmap包对运算结果进行可视化展示,在Rstudio中实现。由于采用高斯函数作为核函数,当积分均方误差最小时,采用式(4)计算得到最优带宽为287.18 m,为了方便计算取最优带宽为300 m,线性单元长度取最优带宽的1/10,即30 m[11]。按照空间步长将1 570条路段划分为子路段,其中不足30 m的部分单独路段作为子路段,最后得到2 886条空间子路段lixels,并计算空间子路段的核密度估计值,为了得到可读性更高的结果,将核密度估计值乘以1 000,得到每公里路段的密度估计值,可视化结果见图4。

图4 网络核密度估计图

同时,为比较平面核密度估计与网络核密度估计的效果差异,同样在R语言中运用SpatialKDE软件包对于事故点分布的平面核密度进行分析,可视化结果见图5。结果表明:所有的高值网络核密度路段均位于平面核密度高值范围内。平面核密度分析结果呈现出局部团状聚集的情况,其分布情况与网络核密度分布情况类似,但聚集范围较大,与网络核密度估计结果相比存在过度估计的情况。若使用平面核密度估计识别事故多发点,那么将无法精确地对事故多发点进行现场隐患排查、派驻警力开展专项交通治理。

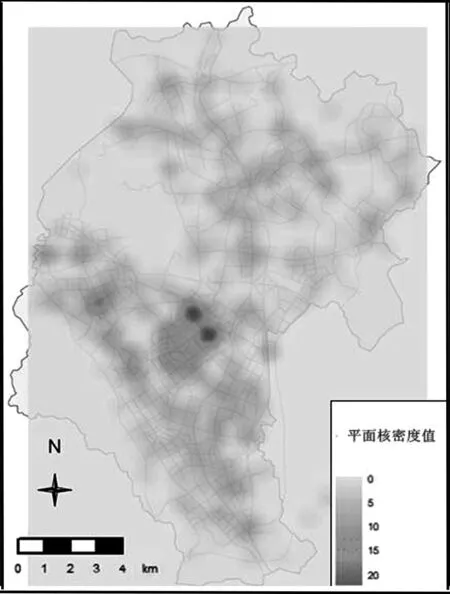
图5 平面核密度估计图

从图4、图5中可以看出,龙华区2018—2020年的交通事故具有明显的空间聚集特征。为了进一步识别高密度路段,一般采用经验法设定鉴别阈值、分位数法、Jenks自然间断点分级法、K-means聚类法等。

本文采用K均值聚类算法(K-means Clustering Algorithm)将路段的核密度估计结果进行分类,采用碎石图,即手肘法则(elbow method)确定最优聚类数,以聚类数为x轴,此处选用1～10作为聚类数量,y轴为各个值到簇中心的平方和,可视化结果见图6。图中点划线指的是在特定聚类数下误差平方和,可见将路段核密度估计值分为4类是最优聚类结果。

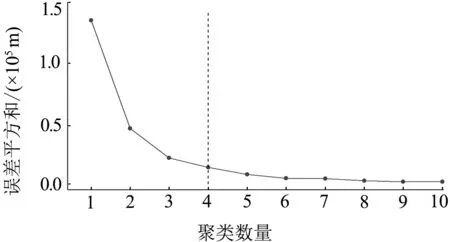
图6 K-means碎石图

该方法所得的分级聚类结果可满足簇内数据差异最小而同时达到簇间数据差异最大的性质,使得误差平方和(Sum of Square Error, SSE)达到局部最小,K-means误差平方和为:

(6)

式中:x为各路段的密度值;ci为所指定划分的聚类簇,此处选取的聚类簇为1～10。从式(6)中可以看出K均值聚类刻画了簇内样本围绕均值向量的紧密程度,SSE值越小,簇内样本相似度越高。通过基于路段密度值之间的相似性进行迭代,使得目标函数SSE最小,最终得到指定聚类簇。

本文通过K-means聚类分析将网络核密度值分为4类,分别对应一级密度路段、二级密度路段、三级密度路段以及四级密度路段,见图7。从图7可以发现,事故密度高值区域多集中在龙华街道中心区域以及大浪街道中心区域,并且分散于各个交叉点处。使用K均值聚类算法进行划分所划定的一级密度路段容易引起注意,在聚类分级的基础上事故密度高值区域相对于图4更为突出。然而该分类方法仅根据密度值之间的数据特征进行分级,并非统计学意义上的风险路段,且该方法忽略了路段间的空间关系,因此使用K均值分级并不能最终确定事故多发路段。

图7 基于K-means聚类的网络核密度估计

3.2 基于网络核密度的局部自相关分析

本文在网络核密度计算结果的基础上,采用R语言中spdep包对路段进行空间自相关分析,选取网络核密度分析中子路段的密度估计值作为计算Local Moran′sI的要素属性值,并使用网络距离的倒数作为空间权重矩阵,将邻近范围内具有相似密度属性的子路段进行合并,最终确定事故多发聚集路段以及异常路段。将置信区间在99%以上的路段绘制Local Moran′sI散点图(图8), 其中Local Moran′sI为两者之间线性关系的斜率, 并将事故多发点鉴别结果在道路网空间进行可视化展示,见图9。

图9 基于NKDE及Local Moran′s I的事故黑点鉴别结果

本文将高值聚类区域100%覆盖K-means聚类分级的一级高值路段,并对相关性显著的高值路段进行合并。高-高聚类区域除零散分布在各个交叉口及路段外,事故多发点主要集中在3个区域,分别为以龙华街道为中心的区域、大浪街道核心区域、三个街道连接处的交叉口区域。异常值(高-低聚类、低-高聚类)则分布较为零散,且数量较少,由于其不具备明显的高值聚类结果,本文对异常值不予关注,其形成与交通事故的偶然性相关。

为分析各聚类簇的事故特点,将各聚类簇由右至左、由上至下分别命名为聚类簇1、聚类簇2、聚类簇3,其具体信息见表1、表2。

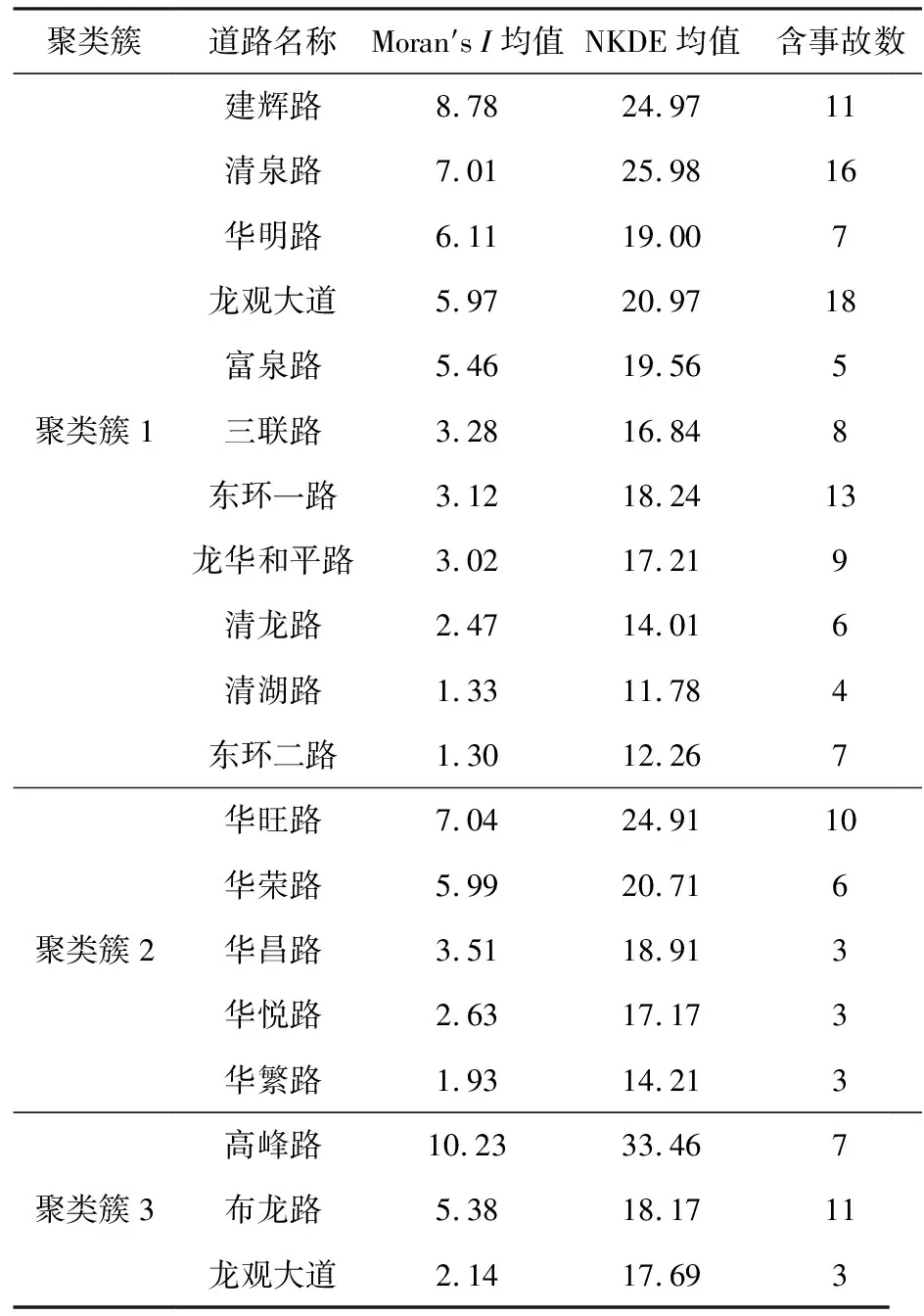
表1 事故多发聚类簇路段具体信息

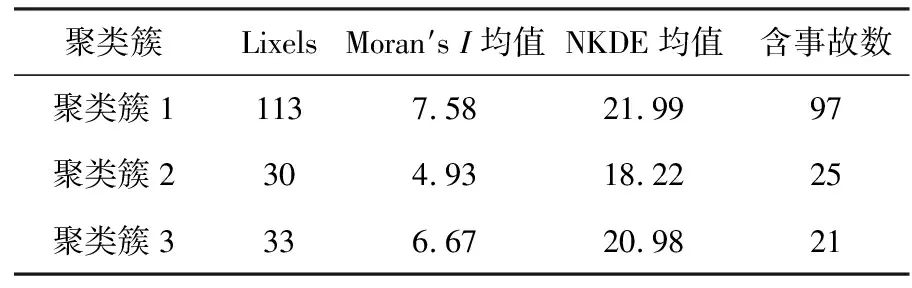
表2 事故多发聚类簇具体信息

3个聚类簇均为龙华区的老城区,作为机动化发展速度较快的老城区,其建设初期主要以机动车通行需求为主,因此忽略了非机动车通行。3个聚类簇发生的143宗事故中,82宗为伤亡事故,均涉及弱势交通参与者;涉及非机动车事故69宗,占比48.25%,其中,涉及无号牌非机动车事故50宗;涉及行人事故13宗,占比9.09%。该区域普遍存在非机动车道建设不完备,部分路段存在人行道、非机动车道宽度不足等问题。随着非机动车通行需求的增大,机非混行的情况日益突出,且由于缺乏号牌登记基础,无号牌非机动车逆行、闯红灯等违法行为无法得到约束。此外,3个聚类簇城中村密集,通行需求较大,内部道路密度高,且交叉口较多,在交通组织不到位、交通参与者不遵守交通规则的情况下,存在大量交通冲突,安全隐患突出。

因此建议通过对3个聚类簇的非机动车道开展隐患排查工作,保证行人及非机动车路权,同时强化全民安全培训教育,加强3个聚类簇合围路段的电子警察、巡警等警力配置,强化电动车上牌、非机动车及行人违法行为劝阻,优化交叉口信号配时以减少交通冲突[24]等。

以聚类簇1中识别到的事故多发路段——建辉路为例,该路段途径城中村高坳新村,人流及非机动车流量较大,且为长下坡路段,道路全段未配置非机动车道,部分路段存在人行道中断、电线杆置于道路内部阻碍车辆通行的情况,且该路段交通秩序混乱,非机动车、机动车长期占道停车,导致行人、非机动车与机动车混行现象突出。该路段已被列为2021年深圳市市级督办隐患治理路段。建议通过压缩机动车道宽度增设“机非共板”非机动车道,通过增加隔离护栏,保障非机动车驾驶员路权,实现机非分离;加强道路全段隐患排查,保证人行道连续性、清除路面障碍物等;增加该路段路面执法力量,清除路面占道停车、劝阻行人及非机动车横穿马路的违法行为。

4 结论

本文以深圳市龙华区2018—2020年1 105例交通事故数据及道路网络数据为基础,对比了传统平面核密度方法及网络核密度方法的事故点位的空间分布情况,采用K-means聚类对网络核密度估计值进行分级,为进一步在考虑路段间的相关关系,引入Local Moran′sI对网络核密度估计值进行空间聚类分析,最终实现事故多发点的识别,具体结论如下:

(1) 基于网络核密度的事故多发点识别方法在道路网空间内对事故点进行核密度估计,结果较平面核密度估计更为精确且符合实际,适用于识别交通事故多发路段,结果表明以龙华街道为核心的龙华中心区事故密度最高。

(2) 通过K-means聚类可对网络核密度估计值进行分级,通过分级使得高密度路段更凸显,然而该方法忽略了临近路段的相关关系,且不具备统计学意义。

(3) 用Local Moran′sI对网络核密度估计值进行空间聚类分析,结果表明该方法在100%覆盖一级路段的基础上将临近高密度路段进行合并,在99%置信区间上最终识别3个聚类簇,具有良好的事故多发点识别效果。

本文在道路空间尺度上研究事故多发点,旨在有限社会资源的前提下,有针对性地进行治理,实现警力资源分配和道路改善措施,从而降低事故发生率,提高道路交通安全水平。但受样本数据时间跨度短及样本不足的限制,本文仅考虑了空间尺度,忽略了时间维度的分析,未来将在考虑时空尺度的基础上进一步建立时空单元与事故黑点的关联性。