转折角对 Z 形通道印刷电路板式换热器中二氧化碳流动与换热特性的影响
沈佳飞 王波 周秋平 王雅亮 成金东
摘要:針对超临界二氧化碳气冷堆核电系统中 Z 形通道印刷电路板式换热器的优化设计,通过数值模拟研究转折角对印刷电路板式换热器中二氧化碳流动和换热特性的影响规律,分别拟合出摩擦因子和努塞尔数的计算关联式,分析传热过程的热阻,并讨论换热器的综合性能。结果表明,摩擦因子和对流换热系数均随转折角的增大呈抛物线规律增长,在转折角小于 20 °时增长较慢。导热热阻占总传热热阻的 4.16%~16.02%,并随二氧化碳质量流率和转折角的增大而升高,在印刷电路板式换热器的传热计算中,不应被忽略。随着转折角的增加,通道中努塞尔数的增长幅度小于摩擦因子的增长幅度,传递相同热量的泵送功率增大,但所需换热面积减小,换热器的制造成本下降,实际应用中需进一步通过技术经济分析以选取最佳转折角。为了控制通道中流动阻力占进口压力的比例,转折角以不超过 20 °为宜。
关键词:印刷电路板式换热器;转折角;二氧化碳;流动阻力;传热
中图分类号: TK 172 文献标志码: A
Effect of turning angle on flow and heat transfer characteristics of carbon dioxide in zigzag printed circuit heat exchangers
SHENJiafei1,WANG Bo1,ZHOU Qiuping2,WANGYaliang1,CHENG Jindong1
(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China;2. Zhejiang Dun'an Machinery and Electronics Technology Co., Ltd., Shaoxing 311800, China)
Abstract: Toachievetheoptimaldesignofzigzagprintedcircuitheatexchanger (PCHE) inthe supercritical carbon dioxide gas-cooled reactor nuclear power system, the influence of the turning angle on the flow and heat transfer characteristics of carbon dioxide in PCHEs was studied by numerical simulation,andthecorrelationsforFanningfrictionfactorandNusseltnumbercalculationwere obtained. The thermal resistance of the heat transfer process was analyzed, and the comprehensive performance of the heat exchanger was discussed. The results show that the Fanning friction factor and convective heat transfer coefficient both increase parabolically with the increase of the turning angle, and the growth is relatively slow when the turning angle is less than 20°. The thermal conductionresistance accounts for 4.16% ~ 16.02% of the overall thermal resistance, and it increases with the increase of the mass flow rate and the turning angle. It should not be ignored in the heat transfer calculation of printed circuit heat exchanger. With the increase of the turning angle, the increase of the Nusselt number is smaller than that of the Fanning friction factor. The pumping power for transferring the same heat increases, but the required heat exchange area decreases. The manufacturing cost are reduced, and in practical applications, further techno-economic analysis is required to select the optimal turning angle. To control the proportion of the flow resistance in the channel to the inlet pressure, the turning angle should not exceed 20° .
Keywords: printed circuit heat exchanger ; turning angle ; carbon dioxide; flow resistance; heat transfer
印刷电路板式换热器( printedcircuitheatexchanger ,PCHE)是一种高效紧凑式换热器,工作温度范围广,承压能力可达60 MPa,在相同换热条件下比传统管壳式换热器的体积减小约85%,有利于降低传热过程的温差和不可逆损失,可用于太阳能热发电、核电和船舶液化天然气供应等系统中[1-3]。PCHE 芯体由多层蚀刻有流体通道的金属板片经扩散焊接制成,通道型式是影响 PCHE 性能的关键因素,有直通道、Z 形通道、 S 形翅片通道和翼型翅片通道等结构。 Chai 等[4]通过数值模拟研究了半圆形截面直通道 PCHE 内超临界二氧化碳(supercritical carbon dioxide , S-CO2)的流动和换热特性,发现局部对流放热系数从入口处开始沿流动方向迅速下降,然后保持稳定,存在明显的入口效应。李磊等[5]比较了不同通道 PCHE 中氦气的流动特性,发现半圆形截面 Z 形通道 PCHE 的阻力系数大于直通道。 Chu 等[6]对 Z 形通道 PCHE 中 S-CO2和水的换热进行了实验研究,获得了努塞尔数和摩擦系数的计算关联式。谢瑶等[7]研究了 PCHE 中液化天然气的传热系数与流动阻力随质量流率、热通量和温度的变化规律。 Cheng 等[8]研究了 Z 形通道 PCHE 预冷器中 S- CO2和水的换热,分析了工质流量和进口温度对流动阻力、换热系数、温度效率的影响。 Wen 等[9] 研究了波形通道 PCHE 中,波形通道的波幅和波长对 S-CO2流动和传热性能的影响,结果表明,相对较小的波幅有利于提高综合性能。宋丹等[10] 对超临界液化天然气在错列 S 形通道 PCHE 中的对流换热过程进行了数值模拟,分析了拟临界工况附近的对流换热特征。 Ma 等[11]研究了翅片横向节距、纵向节距和有无端壁圆角对翼型翅片通道 PCHE 热工水力性能的影响。针对典型应用场景,氦气[12-14]、超临界甲烷[15-16]、超临界二氧化碳[17-19]和熔盐[20-21]等工质在 PCHE 中的流动和换热特性研究受到广泛关注。
在采用 S-CO2冷却反应堆并直接通过 S-CO2布雷顿循环发电的新一代气冷堆核电系统方案中,普遍采用 PCHE作为回热器,其优化设计有利于提高循环效率。在不同通道结构的 PCHE 中, Z 形通道 PCHE制造难度和成本较低,传热性能和应用前景较好[22]。通道转折角是 Z 形通道 PCHE 的重要结构参数,对 PCHE 性能的影响尚需进一步研究。因此,本文针对 S-CO2气冷堆核电系统中低温回热器的传热问题,通过数值模拟分析不同转折角 Z 形通道 PCHE 中二氧化碳的流动和换热特性,为回热器的优化设计和性能实验提供参考。
1 物理模型和数值方法
1.1 物理模型
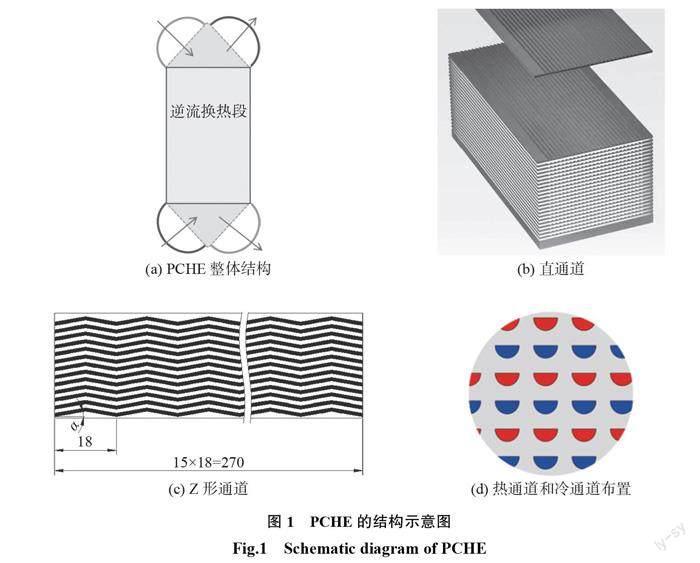
图1(a)为逆流换热 PCHE 整体结构示意图,逆流换热段芯体的直通道结构如图1(b)所示,Z 形通道结构如图1(c)所示。冷流体和热流体通道均为半圆形截面,上下分层交替布置,如图1(d)所示。通道截面半径1.0 mm,水平方向节距3.2 mm,高度方向节距2.2 mm;每个 Z 形通道沿流动方向节距为18 mm ,共15个节距,总节距270 mm。 Z 形通道转折角分别为0(直通道),5,10,15,20,30,45°。换热器材料为316L不锈钢,导热系数为16.2 W/(m?K)。
1.2 網格模型
鉴于 Z 形通道 PCHE 通道布置的周期性特征,并假定热流体和冷流体在各自流动通道中的流量分配均匀,选取图2所示双层通道换热单元为数值模拟对象,热通道在上,冷通道在下,不同参数的二氧化碳逆向流过上下通道进行换热,固体域截面宽3.2 mm 、高4.4 mm、总节距270 mm。图2(b)为其中1个节距范围内的三维结构。采用 ICEM 软件对固体域和流体域进行结构化网格的划分,半圆形截面通道采用 O 形网格,流体通道壁面附近进行网格加密。
在数值模拟过程中,对网格进行无关性验证。图3为通道转折角=30° , 冷通道和热通道中二氧化碳质量流率 G=200 kg/(m2·s),采用不同网格尺寸时,冷通道中流体压降和对流换热系数的计算结果。当网格数达到6191874以后,压降和对流换热系数的计算结果变化十分缓慢,网格数进一步增加到10751736,计算结果相对偏差仅为0.16%和0.51%。因此,该工况下的模拟应选取网格数量为6191874的网格模型。
1.3 边界条件
PCHE 固体域上下壁面和左右壁面设置为周期性边界条件,进口端和出口端壁面设置为绝热边界条件,流体通道的壁面为流固耦合界面。流体域入口采用质量流量入口,出口采用压力出口。热侧二氧化碳入口温度和压力分别为553.15 K 和3.2 MPa,冷侧二氧化碳入口温度和压力分别为381.15 K 和10.5 MPa。冷侧和热侧的入口质量流率相等,质量流率的范围为100~400 kg/(m2?s)。
1.4 物性参数
二氧化碳的热物理性质随压力和温度变化。由于 PCHE 进口二氧化碳的压力高,进出口压差和进口压力的比值较小,故近似认为热通道和冷通道中二氧化碳的物性参数仅随温度变化。通过 REFPROP 软件分别查取10.5 MPa 和3.2 MPa 压力下,350~600 K 范围内二氧化碳的密度ρ、动力黏度μ、定压比热容 cp 和导热系数λ, 并拟合为关于温度 T 的函数,结果如表1所示,拟合优度 R2均高于0.97。
1.5 计算模型与求解方法
在本文研究的工况范围内,二氧化碳在 Z 形通道中流动的雷诺数均大于2000,湍流模型采用 k-ε模型,近壁区采用标准壁面函数。采用 SIMPLE 算法实现速度与压力的耦合求解,变量梯度采用 Least Squares Cell Based 方法求解,压力方程采用标准离散格式,动量方程和能量方程的离散采用二阶迎风格式,湍流方程的离散采用一阶迎风格式,所有变量收敛精度为10?6。该数值模拟方法已广泛用于 PCHE 中二氧化碳传热特性研究,数值模拟与实验结果吻合较好[14,23]。Wang等[24]也对本文的模型进行了验证,分析表明,计算模型比较合理。
1.6 数据处理
流体通道的水力直径
式中: V 表示流体通道的体积;A 表示流体通道的壁面积。
范宁摩擦因子
式中:ΔPf表示流体的压降;表示流体平均密度; L 表示流体通道的长度; u表示通道有效截面上的平均速度。
流体和通道壁面间的平均表面对流换热系数
式中: q 表示平均热流密度;ΔTm表示壁面和流体的平均温差。
流体和通道壁面间对流换热的努塞尔数
式中:λ表示流体的平均导热系数。
本文研究的 PCHE 中,热通道和冷通道结构完全相同,大端温差ΔTd和小端温差ΔTx 的比值小于2,ΔTm可近似采用算术平均温差,即
式中: Tw 表示平均壁温;Tf表示流体平均温度。
以任一侧流体通道壁面积为基准,热流体和冷流体通过金属壁传热的总传热系数
式中:Tf,h为热流体平均温度;Tf,c为冷流体平均温度。
在数值模拟中不考虑污垢热阻,故导热热阻
式中:hh, hc分别为热通道与冷通道的平均表面对流换热系数。
Z 形通道 PCHE 采用不同通道转折角,会影响流体和通道壁面间的平均表面换热系数,以及流体的流动阻力,所以,采用综合评价因子ζ评价Z 形通道强化换热的综合性能
ζ=ΔP(ΔPfr) f = Nf(u)/(/)fref(Nur)ef(8)
式中:下标 ref 表示参比通道,本文选取转折角为0°的直通道为参比通道。
在相同的流体进口质量流率和温度下,ζ可以反映传递相同热量时不同转折角 PCHE 中流体流动阻力的高低[25]。
2 结果与分析
2.1PCHE 中二氧化碳的流动特性
2.1.1 PCHE 中二氧化碳的压力分布
为了探讨转折角对二氧化碳流动和换热特性的影响,对直通道 PCHE 和转折角为5,10,15,20,30,45°的每一种 Z 形通道 PCHE,分别模拟二氧化碳质量流率为100,150,200,250,300,350,400 kg/(m2?s)的7个工况。模拟结果表明,在所有49个工况中,基于每个通道内二氧化碳平均热物性计算所得流动雷诺数最低为5031,最高为20370,均处于湍流状态。
热通道和冷通道中二氧化碳的压力沿流动方向都近似线性变化。以转折角30°、质量流率250 kg/(m2·s)的工况为例,冷通道和热通道中二氧化碳的压力分布分别如图4(a)和(b)所示。从图中可以看出,冷通道中二氧化碳的压力从10.5 MPa 线性下降到10.4874 MPa,流动阻力12.6 kPa,流动阻力和进口压力的比值为1.2‰;热通道中二氧化碳的压力从3.2 MPa线性下降到3.1546 MPa,流动阻力45.4 kPa,流动阻力和进口压力的比值为14.2‰。
2.1.2转折角对二氧化碳流动压降的影响
通道中二氧化碳的压降随质量流率和转折角的增大而增大。如图5所示,在400 kg/(m2·s)的质量流率下,对转折角为0,5,10,15,20、30,45°的 PCHE,冷通道二氧化碳的压降分别为6.881,7.035,7.811,9.947,13.796,29.592,86.581 kPa,与冷通道二氧化碳进口压力的比值分别为0.66‰,0.67‰,0.74‰,0.95‰,1.31‰,2.82‰,8.25‰;热通道二氧化碳的压降分别为23.889,24.483,27.234,34.952,50.552,107.179,316.088 kPa ,与热通道二氧化碳进口压力的比值分别为7.46‰,7.65‰,8.51‰,10.92‰,15.80‰,33.49‰,98.78‰;热通道二氧化碳的压降是冷通道的3.47~3.65倍。由此可见,冷通道和热通道结构相同、质量流率相等的条件下,冷通道二氧化碳进口压力高,流动阻力小,而热通道二氧化碳进口压力低,流动阻力大,在 PCHE 设计中可增大热通道流通面积以控制流动阻力。
2.1.3转折角对流动通道摩擦因子的影响
二氧化碳在 PCHE 通道中流动的摩擦因子随转折角和质量流率变化的规律如图6所示。在每个模拟工况中,热通道和冷通道的转折角和质量流率相同,摩擦因子也接近,而热通道中二氧化碳的流动阻力高,主要是由热通道中二氧化碳的压力低、比容大引起的。对一定转折角的 Z 形通道,由于流动进入紊流光滑管区,摩擦因子与雷诺数负相关,质量流率越大,雷诺数越大,摩擦因子越小。在相同的质量流率下,Z 形通道转折角越大,摩擦因子越高,这是因为随着转折角的增大,流体通过转折角处时方向变化更急,流动截面上速度不均匀性更大,流动分离加剧,流体对前方壁面的碰撞增强,再加上分离区存在二次流,导致能量耗散,增加局部阻力[26]。从图 6 中还可以看出,摩擦因子随转折角呈抛物线规律变化。在一定的质量流率下,直通道的摩擦因子最小;当 Z 形通道转折角小于 20 °时,摩擦因子随转折角的增大而缓慢增大;当转折角大于 20 °时,随着转折角的增大,摩擦因子大幅增长。以质量流率400 kg/(m2·s)的工况为例,直通道 PCHE热通道中二氧化碳平均密度34.79 kg/m3,摩擦因子为0.01176,流动阻力为23.889 kPa;转折角20°的 Z 形通道 PCHE 热通道中二氧化碳平均密度34.99 kg/m3,摩擦因子增大到0.02351,流动阻力增大到 50.552 kPa ;当转折角为45°时,热通道中二氧化碳平均密度35.32 kg/m3,摩擦因子达到0.11165,流动阻力高达316.088 kPa。流动阻力增加的幅度显著超过摩擦因子增加的幅度,这是因为在相同的总节距下,流动通道总长度和转折角的余割值成正比,转折角越大,不仅摩擦因子增加,流动通道也越长;转折角为45°时,在相同的总节距下,其流动通道长度是直通道的1.414倍。在不同转折角下,热通道内二氧化碳的平均密度略有变化,是影响热通道流动阻力的次要因素。因此,將转折角控制在20°以下,有利于避免过大的流动阻力。
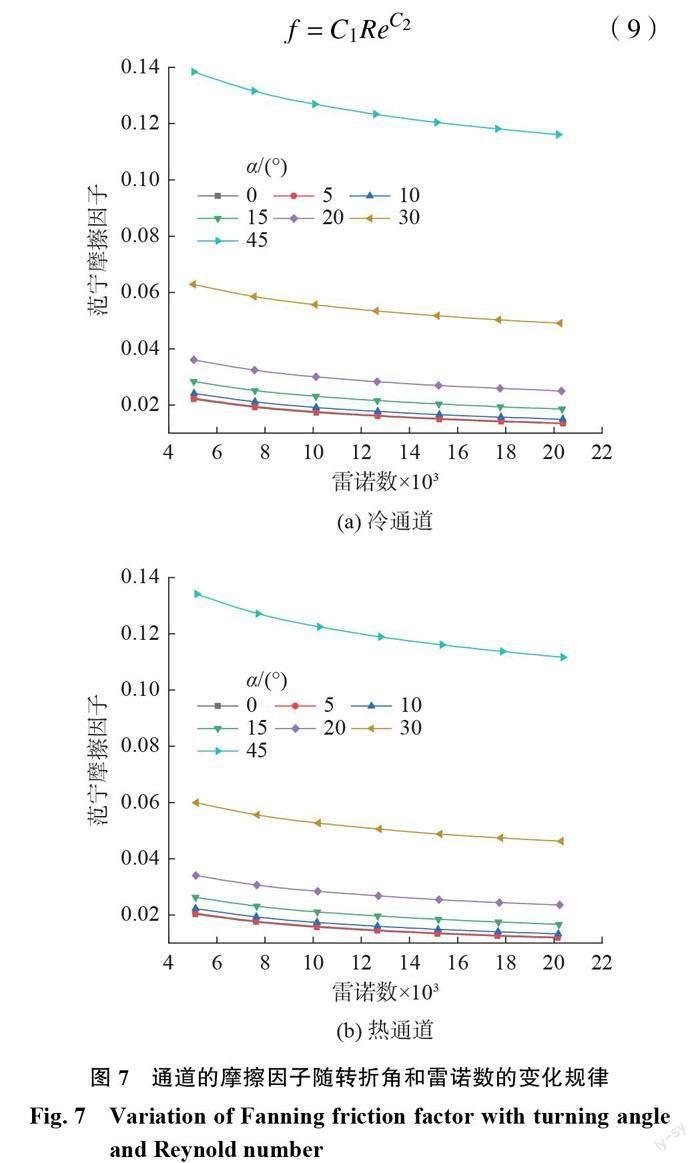
通道内二氧化碳流动的摩擦因子与雷诺数的关系如图7所示。在本文研究的每一个工况下,冷通道和热通道中二氧化碳的质量流率相同,尽管冷通道中二氧化碳压力高、温度低,热通道中二氧化碳压力低、温度高,两侧流体的动力黏度却很接近,相对偏差都在3%以内,因而两侧流动的雷诺数也非常接近。在相同的雷诺数下,冷通道中二氧化碳流动的摩擦因子比热通道高约3%~14%;转折角越大,两侧的摩擦因子相差越小。这可能是因为冷通道中二氧化碳温度沿流动方向不是线性变化,进口端二氧化碳的温度上升较快,出口端温度上升较缓,按平均温度查取密度后计算得到的平均速度和动压略微偏小,使摩擦因子偏大一点。
2.1.4流动通道摩擦因子与雷诺数的关联式
对摩擦因子和雷诺数进行非线性拟合
f = C1ReC2(9)
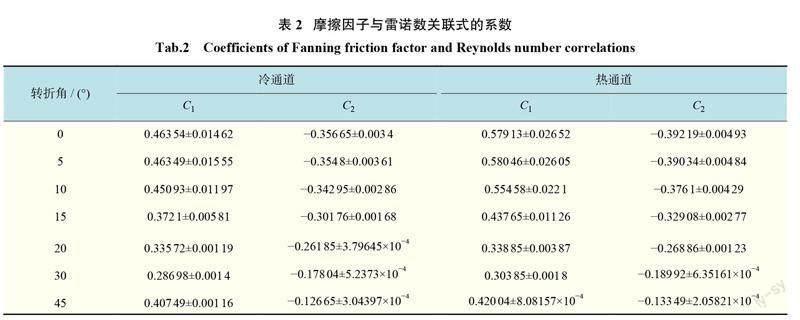
得到不同转折角 Z 形通道 PCHE 中冷通道和热通道摩擦因子与雷诺数之间关联式的系数 C1和 C2,如表2所示。
2.2PCHE 中二氧化碳的换热特性
2.2.1 PCHE 中二氧化碳的温度分布
各工况下热通道中二氧化碳的温度沿流动方向近似线性下降,冷通道中二氧化碳在入口端沿流动方向温度上升较快,然后平稳增长;冷通道入口端的传热温差较大,往出口端逐渐减小,并在较大范围内保持基本稳定。以转折角30°、质量流率250 kg/(m2·s)条件下 Z 形通道 PCHE 内的流动为例,如图8所示,冷通道中二氧化碳温度从 381.15 K 上升到532.35K,热通道中二氧化碳温度从553.15 K 下降到430.41K,高温端传热温差20.8 K,低温端传热温差49.26 K。由于冷侧进口二氧化碳比定压热容为1.490 kJ/(kg?K),热侧出口二氧化碳比定压热容为1.035 kJ/(kg?K),两侧质量流率相等,热侧和冷侧交换一定的热量后,引起的热侧二氧化碳温降,应高于冷侧二氧化碳的温升,而图中温度分布表明低温端冷侧二氧化碳温度反而上升快,传热温差大,这意味著在 PCHE 中由于流动通道的水力直径很小,冷热通道之间的金属壁从高温端向低温端的轴向导热作用不可忽略。结果表明,在回热器设计中如要进一步减小传热温差,还需增加通道长度。
2.2.2转折角对二氧化碳和通道壁面间对流换热的影响
二氧化碳与 PCHE通道壁面间的对流换热系数随通道转折角和质量流率的增大而增大。从图9中可以看出,对流换热系数随转折角呈抛物线规律增大,在一定的质量流率下,直通道的对流换热系数最小;当 Z 形通道转折角小于20°时,对流换热系数随转折角的增大而缓慢增大;当转折角大于20°时,随着转折角的增大,对流换热系数的增幅加大。以质量流率400 kg/(m2·s)的工况为例,直通道 PCHE热通道中二氧化碳和通道壁面间对流换热系数为3268.4 W/(m2·K),转折角20°的 Z 形通道 PCHE热通道中二氧化碳和通道壁面间对流换热系数增大到4004.6 W/(m2·K),转折角45°的 Z 形通道 PCHE热通道中二氧化碳和通道壁面间对流换热系数进一步提高到6724.8 W/(m2·K)。这是由于转折角增大时,流体经过转折角处的流向改变更大,流动分离加剧,对前方壁面的冲刷增强,通过流体扰动更充分地破坏边界层,从而增强与壁面的对流换热。结合图6可知,转折角增大到45°, 对流换热系数增长幅度远远低于摩擦因子增长的幅度,这会引起泵送功率的提高。
从图10中可以看出,努塞尔数随通道转折角和雷诺数的增大而增大。在每个工况中,冷通道和热通道的转折角相等,结构完全相同,但是,在相同的雷诺数下,热通道中努塞尔数比冷通道高出40%~150%,而且雷诺数越小,转折角越大,热通道中努塞尔数比冷通道中努塞尔数增加的幅度越大。
对努塞尔数和雷诺数、普朗特数进行非线性拟合:
Nu = C1ReC2Pr n(10)
式中:Pr为普朗特数; n 为系数,对热通道, n 取0.3,对冷通道, n 取0.4。
不同转折角 Z 形通道 PCHE 中冷通道和热通道中努塞尔数关联式的系数,如表3所示。
2.2.3转折角对导热热阻的影响
本文研究的 PCHE 中上下2个相邻的半圆形截面冷热通道之间的壁厚是渐变的,可采用等效壁厚法计算冷热通道之间的导热热阻[1,27]。等效壁厚
tw = t -(11)
式中: t 为冷热通道之间的最大壁厚,对本文研究的 PCHE,其值为0.0022 m;r 为半圆形截面的半径。
导热热阻
rw =(12)
式中:λw 为金属的导热系数。
采用等效壁厚法计算得到冷热通道之间金属壁的导热热阻为8.7321×10?5 m2·K/W。
通过数值模拟获得的总传热系数随转折角和质量流率的变化规律如图11所示。
根据总传热系数、热通道的平均表面对流换热系数和冷通道的平均表面对流换热系数,按照式(7)计算可得传热过程的导热热阻。同一转折角下,导热热阻随质量流率的变化很小,近似为一个定值。对于转折角0,5,10,15,20,30,45°的Z 形通道 PCHE,计算所得导热热阻分别为7.8522×10?5,7.8283×10?5,7.7639×10?5,7.7213×10?5,7.7565×10?5,7.8764×10?5,7.9214×10?5 m2·K/W,与采用等效壁厚法计算所得导热热阻的相对偏差分别为10.08%,10.35%,11.09%,11.58%,11.17%,9.80%,9.28%。等效壁厚法计算所得导热热阻偏高,其原因可能是等效热阻法是简化计算方法,没有考虑转折角对导热的影响,也没有考虑冷热通道之间的金属壁从高温端向低温端的轴向导热作用。
在相同质量流率下,冷通道中二氧化碳的对流换热热阻在总传热热阻中所占比重较大。以质量流率为100 kg/(m2·s)的工况为例,转折角为0,5,10,15,20,30,45°时,冷通道对流换热热阻分别占总传热热阻的60.04%,60.07%,60.23%,60.88%,61.53%,63.17%,65.31%。随着质量流率的增大,冷通道热阻在总热阻中所占比重略有减小。如图12所示,质量流率和转折角越大,冷通道和热通道的对流换热热阻越小,导热热阻占总传热热阻的比例就越高。在所有的工况中,导热热阻占总传热热阻的比例在4.16%~16.02%之间,表明在 PCHE 的传热计算中,不宜忽略导热热阻。2.3 转折角对 PCHE 综合性能的影响
通过上述分析可知,随着 Z 形通道转折角的增大, PCHE 换热性能增强,同时流动阻力也会增大。为了综合评价转折角对 Z 形通道 PCHE 性能的影响,以直通道 PCHE 作为参比结构,按式(8)计算综合评价因子ζ。
图13为不同转折角 PCHE 的综合评价因子随质量流率的变化规律。从图中可以看出,所有转折角下 PCHE 的综合评价因子均小于1,表明摩擦因子的增长幅度大于努塞尔数的增长幅度。在相同的冷热流体质量流率和进出口温度下,与直通道 PCHE 相比,采用 Z 形通道 PCHE 时实现相同传热量,克服流动阻力所消耗的功率随着转折角的增大而升高,导致运行成本增加。但是,随着转折角的增大,努塞尔数提高,所需换热面积减小,换热器结构更紧凑,重量更轻,这将减小换热器的制造成本。在 PCHE 设计时,需综合考虑制造成本和运行成本,以及对发电循环效率的影响。结合图5所示冷通道和热通道流动阻力占冷通道进口压力的比例,转折角以不超过20°为宜,否则过大的流动阻力会降低布雷顿发电循环的效率。
3 结论
针对 S-CO2气冷堆核电系统中低温回热器的传热,通过数值模拟分析不同转折角 Z 形通道 PCHE 中二氧化碳的流动和换热特性,得出如下结论:
a.冷通道和热通道内二氧化碳流动和换热过程中,摩擦因子和对流换热系数均随转折角的增大呈抛物线規律变化,当 Z 形通道转折角小于20°时,摩擦因子和对流换热系数随转折角的增大而缓慢增大;当转折角大于20°时,随着转折角的增大,摩擦因子和对流换热系数增长幅度加大,且对流换热系数增长幅度显著低于摩擦因子增长幅度。
b.在 PCHE冷通道和热通道结构相同、质量流率相等的条件下,热通道中二氧化碳的流动阻力和对流换热系数显著高于冷通道,可考虑通过增加热侧二氧化碳流通截面积,降低热通道中二氧化碳流速和阻力。
c.质量流率和转折角越大,导热热阻占总传热热阻的比例越高。在本文研究的工况中,导热热阻占总传热热阻的比例在4.16%~16.02%之间,在 PCHE 的传热计算中,不宜忽略导热热阻。采用等效壁厚法计算所得的导热热阻相对偏大。
d.不同转折角下 PCHE 的综合评价因子均小于1,意味着在相同的质量流率和进出口温度下,随着转折角的增加,传递相同热量的泵送功率增大,但所需换热面积减小,换热器体积、重量和制造成本下降,在实际应用中应通过技术经济分析以选取最佳转折角。结合通道中流动阻力占进口压力的比例,转折角以不超过20°为宜,以免流动阻力过大导致布雷顿发电循环效率下降。
参考文献:
[1]徐哲, 张明辉, 段天应, 等.超临界二氧化碳在印刷电路板式换热器内的流动换热特性研究[J].原子能科学技术, 2021, 55(5):849–855.
[2] KLEMES? J J. Compact heat exchangers for energy transfer intensification: low grade heat and fouling mitigation[M]. Boca Raton: CRC Press, 2016:101–104.
[3] NIKITINK,KATOY,NGOL. Printedcircuitheat exchanger thermal-hydraulic performanceinsupercritical CO2experimentalloop[J].InternationalJournalofRefrigeration, 2006, 29(5):807–814.
[4] CHAIL,TASSOUSA. Numericalstudyofthe thermohydraulicperformanceofprintedcircuitheat exchangersforsupercriticalCO2Braytoncycle applications[J]. Energy Procedia, 2019, 161:480–488.
[5]李磊, 杨剑, 马挺,等.印刷电路板通道的高温传热和阻力特性研究[J].工程热物理学报, 2014, 35(5):931–934.
[6] CHU W X, LI X H, CHEN Y T, et al. Experimental study on small scale printed circuit heat exchanger with zigzag channels[J]. HeatTransferEngineering, 2021, 42(9):723–735.
[7]谢瑶, 李剑锐, 胡海涛.印刷电路板式换热器内超临界甲烷流动换热特性模拟[J].化工学报 , 2021, 72(S1):203–209.
[8] CHENGKY,ZHOUJZ,ZHANGHZ,etal. Experimentalinvestigationofthermal-hydraulic characteristics of a printed circuit heat exchanger used as a pre-coolerforthesupercriticalCO2Braytoncycle[J]. Applied Thermal Engineering, 2020, 171:115116.
[9] WEN Z X, LV Y G, LI Q, et al. Numerical study on heat transfer behavior of wavy channel supercritical CO2 printed circuitheatexchangerswithdifferentamplitudeand wavelengthparameters[J]. InternationalJournalofHeat and Mass Transfer, 2020, 147:118922.
[10]宋丹, 蒋庆峰, 冯国增, 等.超临界 LNG 在错列 S 形翅片微通道的流动传热特性研究[J].低温与超导 , 2021,49(1):16–21.
[11] MA T, XIN F, LI L, et al. Effect offin-endwall fillet on thermal hydraulic performance of airfoil printed circuit heat exchanger[J]. AppliedThermalEngineering, 2015, 89:1087–1095.
[12] MCCORMACK D. The application of printed circuit heat exchanger technology in the pebble bed modular reactor demonstration plant[C]//Proceedings of ASME Turbo Expo 2001: Power for Land, Sea, and Air. New Orleans: ASME, 2001:2001-GT-0473.
[13] KIMIH,NOHC. Physicalmodeldevelopmentand optimal design of PCHE for intermediate heat exchangers in HTGRs[J]. Nuclear Engineering and Design, 2012, 243:243–250.
[14] KIMDE,KIMMH,CHAJE,etal. Numerical investigationonthermal –hydraulicperformanceofnew printedcircuitheatexchangermodel[J].Nuclear Engineering and Design, 2008, 238(12):3269–3276.
[15]李瑋哲, 林文胜.超临界甲烷在印刷电路板换热器中加热过程模拟[J].低温工程, 2017(5):60–64,74.
[16]贾丹丹, 赵忠超, 张永, 等.超临界 LNG 在印刷板式汽化器微细流道内的流动与换热性能数值研究[J].船舶工程, 2017, 39(5):35–40.
[17] BAEKS,KIMJH,JEONGS,etal. Developmentof highlyeffectivecryogenic printedcircuitheatexchanger (PCHE) with low axial conduction[J]. Cryogenics, 2012, 52(7/9):366–374.
[18]张海燕, 郭江峰, 淮秀兰, 等. PCHE 内轴向导热对局部换热性能的影响研究 [J].化工学报 , 2019, 70(12):4590–4598.
[19]王绩德, 冯岩, 韩东江.超临界二氧化碳动力循环在钠冷快堆中的应用综述[J].核科学与工程, 2019, 39(2):289–297.
[20] SHI H Y, LI M J, WANG W Q, et al. Heat transfer and friction of molten salt and supercritical CO2 flowing in an airfoilchannelofaprintedcircuitheatexchanger[J].InternationalJournalofHeatandMassTransfer, 2020, 150:119006.
[21]何雅玲, 王文奇, 邱羽, 等.熔盐在复杂换热结构内的对流换热特性实验研究及进展[J].科学通报 , 2019, 64(28/29):3007–3019.
[22] KATO Y, NITAWAKI T, MUTO Y. Medium temperaturecarbon dioxide gas turbine reactor[J]. Nuclear Engineering and Design, 2004, 230(1/3):195–207.
[23]高毅超 , 夏文凯 , 龙颖 , 等.管径和转折角对 Z 型 PCHE 换热及压降影响的研究[J].热能动力工程, 2019,34(2):94–100.
[24] WANGB,SHENJF,CHENGJD,etal. Numerical improvement using flow and heat transfer calculations of thezigzaggeometryforcarbondioxidePCHEs[J]. Energies, 2022, 15(8):2831.
[25]顾维藻, 神家锐, 马重芳, 等.强化传热[M].北京:科学出版社, 1990:10.
[26]史以奇, 李凌.螺纹管管内流动与传热的数值模拟[J].上海理工大学学报, 2016, 38(2):133–136,141.
[27] KIMIH,NOHC,LEEJI,etal. Thermalhydraulic performance analysis of the printed circuit heat exchanger usingaheliumtestfacilityandCFDsimulations[J]. NuclearEngineeringandDesign,2009,239(11):2399–2408.
(编辑:石瑛)

