微通道换热器的数值模拟和结构优化

郭春海+陈希良+杨旸+张文武

摘要： 为提高微通道换热器的换热效率，利用COMSOL耦合求解流动和传热方程，对微通道换热器换热特征进行数值模拟.通过分析微通道换热器的温度、微通道的入口与出口的压差以及微通道换热器的总热阻等参数，对其换热性能进行评估.优化微换热器的几何结构可以有效提高换热性能.数值模拟结果表明：当微通道的高宽比为0.8、微通道与间隔的宽度比为0.6、微通道数为71时热阻最小，换热性能最佳.

关键词： 微通道； 传热； 热阻； 压差； 最高温度

中图分类号： TK124文献标志码： B

Abstract： To improve the heat exchange efficiency of microchannel heat exchanger， the flow and heat transfer equations are solved using COMSOL and the heat exchange characteristics of microchannel heat exchanger is numerically simulated. The parameters such as the temperature， differential pressure between inlet and outlet and total thermal resistance of the microchannel exchanger are analyzed， and its heat exchange performance is evaluated. The heat exchange performance can be effectively improved by optimizing the geometry structure of microchannel heat exchanger. The numerical simulation results indicate that the thermal resistance can be minimized and the heat exchange can reach the best performance when the height to width ratio of microchannel is 0.8， the width ratio of microchannel to interval is 0.6， and the channel number is 71.

Key words： microchannel； heat transfer； thermal resistance； differential pressure； maximum temperature

收稿日期： 2014[KG*9〗04[KG*9〗22修回日期： 2014[KG*9〗05[KG*9〗04

作者简介： 郭春海（1980—），男，山东莱芜人，助理研究员，研究方向为计算流体力学及数值传热学，（Email）guochunhai@nimte.ac.cn0引言

随着现代科学技术的发展、加工制造工艺技术的提高以及实际工业生产的需求，小尺度和微尺度传热问题已经越来越受关注.目前，微槽散热器已在超大规模集成电路、超导电机和制冷等方面得到应用.[1]由于芯片的尺寸越来越小，导致芯片功率密度急剧增大，使得芯片内的热流密度非常大，据报道最高可达107 W/m2量级[2]，芯片的工作温度也随之增加；另一方面，电子器件的工作温度在其极限温度70%～80%水平上每增加1%，其可靠性会下降5%.[3]

早在20世纪80年代，TUCKERMAN等[4]就在1 cm×1 cm硅板上开一系列宽50 μm，深302 μm，间隔50 μm的微槽，以水为工作介质进行流动与换热试验，可以散失高达790 W/cm2条件下的热量，同时发现摩擦因数f较经典理论计算略高.CHOI等[5]对内径3～102 μm圆截面微管中水的流动和传热进行试验研究，认为微管中流体流动摩擦因数较常规尺度关联式的预测值小，而Nu数则比DittusBoelter关联式的预测值大.CHEN等[6]采用甲醇作为工质流体，对水力直径57～267 μm的微通道流动特征进行试验研究，传热试验结果表明微通道换热器中强迫对流具有更好的冷却效果.QU等[7]对在1 cm2硅基上微通道宽57和80 μm共轭传热进行数值分析，表明微通道换热器的最高温度分布在其底面，而且得到当Re为1 400时微通道中的流体将不会是充分发展的层流的结论.GAMRAT等[8]对水在矩形微通道中的换热进行二维和三维的数值模拟研究，重点考察进口段效应和对流导热耦合效应的影响.KOU等[9]通过调整微通道的宽度和高度，应用数值模拟对微通道换热器的传热性能进行优化，得到最小的热阻以及随流量变化的最优的微通道宽度和高度.LI等[10]利用三维传热模型分析硅基微通道换热器的传热性能，分析比较微通道数和微通道间隔对传热性能的影响.

尽管许多学者对微通道内流体流动和传热进行广泛研究，但是其相对较高的传热特性和较低的热阻是以大功率消耗、冷却液的高流量和较大压头为代价的.为采用低功率、低流量和小压头达到快速冷却芯片的目的，需要优化设计微通道的几何尺寸，并采用合适的工质流体，使得在最小功耗情况下微通道结构的总热阻最小，以满足芯片的散热要求.

本文数值模拟不同几何参数（包括微通道数量、高宽比、间隔和基底厚度等）下微通道换热器的传热情况，并通过对微通道换热器传热性能的分析比较，给出一种传热效率最优的几何结构，为微通道换热器的设计提供参考.

1数值分析

1.1计算模型

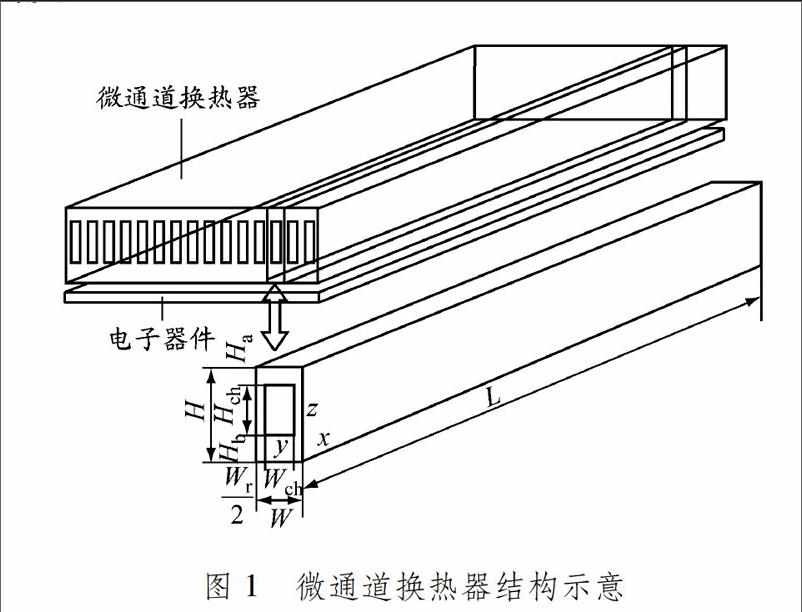
微通道换热器在1 cm×1 cm的基板上加工而成.微通道换热器中微通道的结构相同，沿x，y和z方向单个微通道单元的长、宽、高分别为L，W和H，其结构示意见图1，其中Wch为微通道的宽度，Hch为微通道的高度，Wr/2为微通道中间肋片宽度的一半，Hb为微通道换热器下表面到微通道下底面的高度，Ha为微通道上底面到微通道换热器上表面的高度.

在数值计算过程中，各个微通道的边界条件相同，整个微通道换热器的上表面绝热，下表面给定热流密度，入口处的冷却介质温度为常数；底面产生的热量由肋片通过热传导带走，然后通过微通道中冷却介质的强制对流消散.在数值计算过程中进行如下假设：

1） 流体流动状态为不可压缩的层流，流动过程为稳态.

2） 微通道中的流体流动忽略重力影响和热辐射影响.

3） 冷却介质和基板材料的热属性为常数.

4） 忽略流体的黏度耗散.

1.2控制方程与边界条件

基于以上假设，该共轭传热问题的控制方程如下.

1.3网格划分和计算

利用多物理场仿真软件COMSOL对流动传热过程进行仿真.因计算区域较规则，故采用六面体网格进行划分，计算时采用的网格在x，y和z方向分别为200，28和10.另外，为验证网格的无关性，网格划分时将网格加密到400，70和20，结果表明：加密网格与未加密网格的计算结果相差很小，微槽道中的压降和下表面的平均温度相对误差均小于5%，可以认为数值计算结果不受网格数量变化的影响.

2结果和讨论

2.1理论分析

为评价微通道换热器的传热性能，分析微通道换热器的温度变化和总热阻，其中总热阻 RT=Tmax-TinqwA （10）式中：Tmax为微通道换热器的最高温度；Tin为冷却介质的入口温度；qw为底面的热流密度；A为加热底面的面积.

总热阻RT主要包含3部分：1）热源芯片表面与微通道基底之间的导热热阻Rcond；2）微通道内表面到工质流体间的对流热阻Rconv；3）微通道热沉入口处工质流体的大体积温升热阻Rheat. RT=Rcond+Rconv+Rheat=HksA+1NhconvAc+1Cl （11）式中：N为微通道数量；hconv为冷却介质的对流传热系数；Ac为湿周面积；为质量流量.在上述计算模型中，A=L（NWch+（N+1）Wr） （12）

除热阻外，流体的流动也强烈影响热沉的传热性能.流体在微通道中的流动由压差表征，对于充分发展的层流，由达西方程得Δp=fLDhρl22 （18）式中：Δp为微通道中入口与出口流体的压差；f为摩擦因数.本文中冷却介质为水，ρl=997 kg/m3，Cl=4 187 J/（kg·K），kl=0.613 W/（m·K），运动黏度为温度的函数，νl=2.414 10-8×10247.8T-140 m2/s；基板材料为铜，ks=401 W/（m·K）.微通道换热器的几何参数见表1.

2.2数值模拟结果

影响微通道换热器传热性能的主要因素有热阻和压差，因此分别对这2个参数进行分析.

为验证模拟的准确性，将基片材料为硅、冷却介质为水的3种结构在不同压差下的数值模拟结果与TUCKERMAN等[4]的试验结果进行比较，见表2.由此可知，应用本文模拟方法得到的结果与试验结果一致，说明本文的模拟方法合理.

由于该微通道换热器几何结构比较规整，为减少计算量，各取微通道与间隔的1/2作为计算单元，对一个单元的流动传热进行数值模拟.单元几何结构Wch=Wr=50 μm，Hch=40 μm，Hb=30 μm，Ha=100 μm.计算边界条件为：冷却介质温度T=293 K，热流密度qw=100 W/cm2.

入口流量=10 mg/s时，沿轴向（x方向）中间位置横截面云图见图2.由图2a可知，由于边界黏性影响，壁面处速度为0，中心位置速度最大，在整个截面处的平均速度为0.5 m/s，与分析结果一致.由图2b可知，由于管道内流场的沿程阻力影响，压力呈一定梯度逐渐变小，整个通道中的压力变化约为23 kPa.

a）速度，m/s

b）压力，104 Pa

入口与出口的压差随流量的变化见图3.由式（18）可知，在相同的管道内，出入口的压差与管道内的平均速度成正比，因此也与流量成正比.由图3可知，分析结果与模拟结果一致.由于模拟过程的部分假设和误差的原因，二者在数值上存在一定的误差.

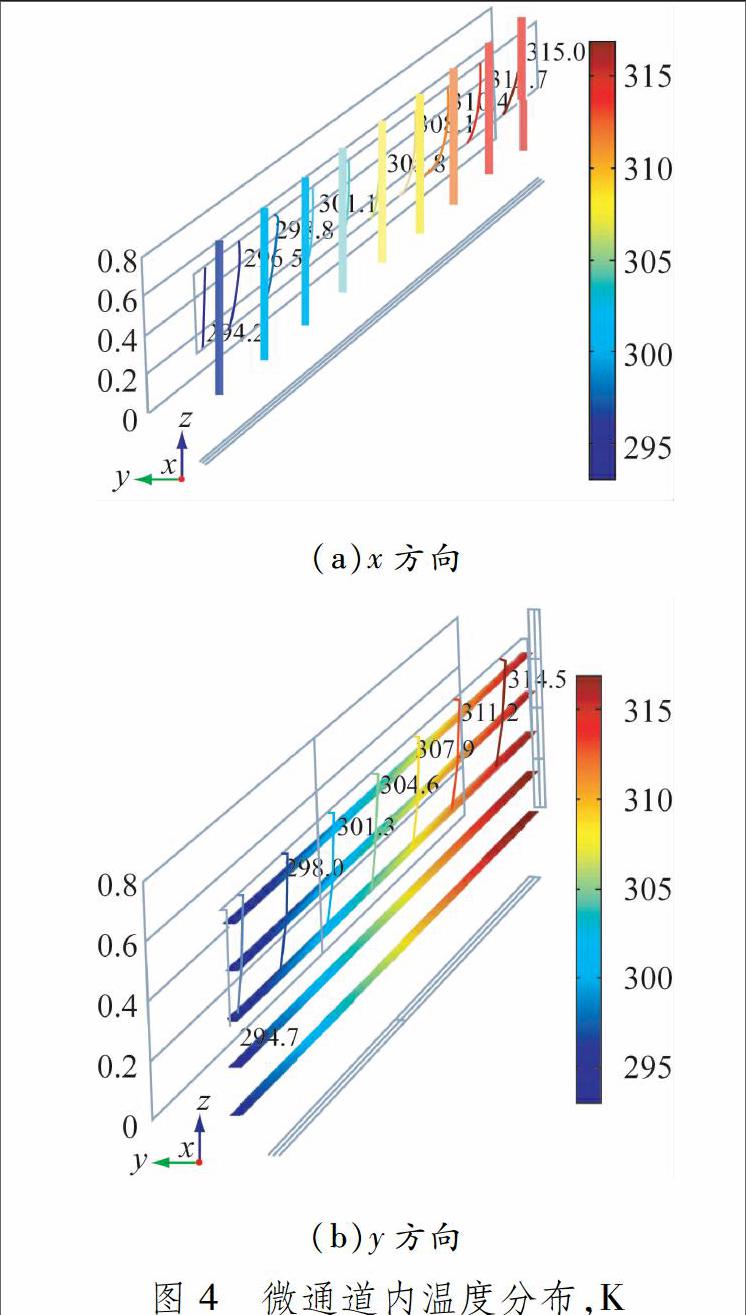
当入口流量=10 mg/s时，微通道内沿x和y方向的温度分布见图4.

（a）x方向

（b）y方向

由图4可知，由于底面热流的存在，水在流动过程中逐渐升温，因此固体域与流体域的温度都沿x方向升高，并且在每个相同位置的截面上温度相同；流体域和固体域的温度相近，温差小于0.5 K.由此也可以看出，微通道内壁面的温度在每个截面处相同.由于热传导的原因，温度场沿z方向变化不大，上表面与下表面温差很小.

该几何结构下总热阻随流量的变化见图5.由式（11）可知，在相同管道内，热阻随流量的增大而降低，分析结果与模拟结果一致.

2.3几何结构优化

微通道高宽比α，微通道与间隔的宽度比β和微通道数N对微通道入口与出口压差Δp的影响见图6.由图6a可知，当β=Wch/（Wch+Wr）和N一定时，若 α=Hch/Wch越大，Δp越小.这是由于若β和N已定，则Wch已定，α越大，Hch越大，从而微通道的水力直径Dh=2HchWch/（Hch+Wch）越大，由式（18）可知，在相同速度下Δp越小.另外，由图6a还可看出，N越大Δp越大，这是因为N=Wtotal/（Wch+Wr），若Wtotal=1 cm，β已定，则N越大，Wch越小，α相同时Hch亦越小，Dh就越小，Δp就越大.由图6b可知，当N和α一定时，β越大Δp越小.这是因为若N已定，则Wch+Wr已定，β越大，Wch越大，Hch越大，Dh越大，Δp越小.另外，由图6b还可以看出，α越大，Δp越小，这也是由Dh变大引起的.由图6c可知，在α一定时，Δp随N的变大而增大，这是由于N增大时，微通道宽度变小，高度也变小，从而Dh变小引起的.微通道高宽比α、宽度比β、微通道数N和底基厚度Hb对总热阻RT的影响见图7.由图7a可知，在β和N一定时，当α<8时总热阻随α的增大而减小，而当α>8时总热阻逐渐增大.这是因为如果β和N已定，Wch就已定，那么α越大，Hch就越大，由式（15）可知Rheat减小，同时流固接触面积增大，Rconv减小，但是Hch变大，H亦变大，使Rcond变大.因此，当α<8时，Rheat和Rconv减小作用强于Rcond的增大，总热阻变小；当α>8时，Rcond的增大作用大，因此RT变大.由图7b可知，若N一定，则当β<0.6时，RT随β的增大而减小，当β>0.6时，RT随β的增大而增大.这是因为若N和α已定，则β越大，Wch越大，流固接触面积增大，Rheat和Rconv变小， 同时Wch越大，Hch变大，H亦变大，Rcond变大.因此，当β<0.6时Rconv和Rheat作用明显，当β>0.6时Rcond作用明显，RT随β变大先减小后变大.由图7c可知，当α一定且β较小时，Wch和Hch都较小，RT较大.当N<71个时，RT随N的增大而减小，当N>71个时，RT随N的增大而增大.这是由于若α和β一定，当N开始增大时，Wch变小，Hch也变小，对流换热面积变小；当N<71个时，N的变化占主导因素，Rheat和Rconv变小，同时Rcond变小，所以RT变小；但当N>71个时，对流换热面积的变化占主导地位，Rheat及Rconv变大，虽然此时Rcond变小，RT仍变大，但此种综合情况下引起的变化不太明显.这点由图7c可以看出，当β=0.5时，二者大致相抵，引起的RT变化也不明显.由图7d可知，随着底基厚度Hb的增大，RT增大，这是由Rcond增大引起的.a）αb）βc）N

3结论

利用三维耦合流动传热模型对强迫对流下微通道换热器的传热过程进行数值模拟，通过比较温度、总热阻以及微通道中的压差等参数对几何结构进行分析，得到以下结论.

几何结构对微通道换热器的性能有巨大影响，通过分析发现，微通道的结构高宽比、宽度比、微通道数和底基厚度对热阻都有影响.当微通道的高宽比为0.8、微通道与间隔的宽度比为0.6、微通道数为71个且底基厚度为0.1 mm时，微通道换热器的换热效果最好，其在0.5 m/s的入口速度下热阻最小为0.36 K/W.参考文献：

[1]罗小平， 陈海洋. 矩形微槽道内对流换热的试验研究[J]. 石油机械， 2009， 37（1）： 17.

LUO Xiaoping， CHEN Haiyang. An experimental study of the convective heat transfer within the rectangular microchannel[J]. China Petroleum Machinery， 2009， 37（1）： 17.

[2]过增元. 国际传热研究前沿——微细尺度传热[J]. 力学进展， 2000， 30（1）： 16.

GUO Zengyuan. Frontier of heat transfer： microscale heat transfer[J]. Advances Mech， 2000， 30（1）： 16.

[3]席有民， 余建祖， 高红霞， 等. 单相液体微槽散热研究进展[J]. 制冷学报， 2008， 29（4）： 2429.

XI Youmin， YU Jianzu， GAO Hongxia， et al. Research development of single phase liquid heat transfer in microchannel[J]. J Refrigeration， 2008， 29（4）： 2429.

[4]TUCKERMAN D B， PEASE R F W. High performance heat sinking for VLSI[J]. IEEE Electron Dev Lett， 1981， 2（5）： 126129.

[5]CHOI S B， BARRON R R， WARRINGTON R O. Fluid flow and heat transfer in micro tubes[J]. ASME Micromechanical Sensors， Actuator & Sys， 1991（32）： 8993.

[6]CHEN Y T， KANG S W. Experimental investigation of fluid flow and heat transfer in microchannels[J]. Tamkang J Sci & Eng， 2004， 7（1）： 1116.

[7]QU W， MUDAWAR I. Analysis of threedimensional heat transfer in microchannel heat sinks[J]. Int J Heat & Mass Transfer， 2002， 45（19）： 39733985.

[8]GAMRAT G， FAVREMARINET M， ASENDRYCH D. Conduction and entrance effects on laminar liquid flow and heat transfer in rectangular microchannels[J]. Int J Heat & Mass Transfer， 2005， 48（14）： 29432954.

[9]KOU H， LEE J， CHEN C. Optimum thermal performance of microchannel heat sink by adjusting channel width and height[J]. Int Commun Heat & Mass Transfer， 2008， 35（5）： 577582.

[10]LI J， PETERSON G P. 3Dimensional numerical optimization of siliconbased high performance parallel microchannel heat sink with liquid flow[J]. Int J Heat & Mass Transfer， 2007， 50（15/16）： 28952904.

[11]KIM S J， KIM D. Forced Convection in microstructures for electronic equipment cooling[J]. J Heat Transfer， 1999， 121（3）： 639645