联合稀疏和低秩表示的医学超声图像去噪

武俊珂　魏国亮　兰兰　蔡贤杰

摘要：为了保持超声图像的边缘和细节特征，同时去除图像中的噪声，提出了一种改进的低秩稀疏矩阵分解模型。首先，通过对数变换将乘性性质的斑点噪声转换为加性噪声；然后引入 L1 范数和改进的低秩正则项，以最小化保真项、正则项为目标函数，迭代恢复出去噪后的超声图像；最后使用指数变换从对数域中还原。将本模型应用于肿瘤超声图像，与一些经典的去噪算法进行比较，得出该模型对消化道粘膜下肿瘤超声图像去噪估计具有良好的适用性和实时性。

关键词：消化道粘膜下肿瘤；超声图像；斑点噪声；去噪估计；低秩稀疏模型

中图分类号：  TP 391.41             文献标志码：  A

Medical ultrasound image denoising based on low-rank and sparse model

WU Junke1，WEI Guoliang2，LAN Lan1，CAI Xianjie3

（1. College of Science， University of Shanghai for Science and Technology， Shanghai 200093， China;2. Business School， Universityof Shanghai for Science and Technology， Shanghai 200093， China;3. School of Optical-Electrical and Computer Engineering，University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： An improved low-rank and sparse matrix decomposition model was proposed to preserve edge， detail features and remove noise in ultrasound images. Firstly， logarithmic transformation was carried out to transform the multiplicative speckle noise into additive noise. Then the L1-norm and improved  low-rank  regularizer term were  introduced  to  iteratively  recover  the  denoised  ultrasound image with the minimisation of the fidelity and regularization term as the objective function. Finally， the exponential transformation was used to restore the resulting graph from the logarithmic domain. The model was compared with some classical denoising algorithms using tumour ultrasound images. The results show that the model has good applicability and realtime for the estimation of ultrasonic image denoising of gastrointestinal submucosal tumours.

Keywords： gastrointestinal submucosal tumors; ultrasound image; speckle  noise; denoising ; low- rank and sparse model

近年來，随着大众健康意识的提升和内镜检查的普及，消化道粘膜下肿瘤（SMT）的检出率逐年提高。超声内镜具有双重检查优势，既能通过内镜清晰地观察粘膜下肿瘤的外部形态，又可通过小探头超声对肿瘤进行扫描，获得更清晰、全面的超声图像[1]。超声内镜扫描的超声图像可以显示病灶管壁及其周围结构，并根据回声信号高低、是否均匀、及与消化道管壁的关系，明确肿瘤的起源层次、范围、浸润深度，是初步诊断消化道粘膜下肿瘤的首选方法。但超声内镜也有不足之处，其成像过程中生成的斑点噪声严重影响了图像的人工判读和后续处理[2]。随着人工智能在内镜诊断领域的发展，医学图片的原始像素提取及有效预处理对挖掘图像特征并预测肿瘤至关重要。总之，基于消化道粘膜下的超声图像去噪处理意义重大。

目前已经将多种滤波算法应用到了医学超声图像处理中，晏满钰等[3]提出了一种基于各向异性扩散方程的改进方法，利用各方向梯度值和图像梯度变化选取不同扩散函数，进一步提高了去噪效果。张聚等[4]针对斑点噪声问题，提出了一种新型的基于小波和双边滤波的去噪算法，经过临床实验证明该算法能够很好地抑制超声中的斑点噪声，并且能保留图像病灶边缘等细节。 Zhou 等[5]提出了采用双边滤波去噪的方法来减少散斑，并验证了该方法的性能，结果表明双边滤波去噪方法在平滑散斑的同时能很好地保护病变边缘。Rahimizadeh等[6]提出了一种改进的线性最小均方误差（LMMSE）估计器，用于降低超声医学图像的斑点噪声，在保持小细节和降低图像不同区域散斑噪声之间可以达到很好的平衡。陈晓东等[7]提出分数阶微分加权的引导滤波算法，利用像素与边缘纹理的关系设计纹理因子，改进引导滤波方法，并对猪胃和猪气管超声图像进行了算法实验，验证了该算法具有良好的适用性。薛双青等[8]提出了将二维变分模态分解和双边滤波相结合的超声图像去噪方法，并实验验证了该方法在去除图像中的噪声和保护细节信息方面效果不错。张光华等[9]提出了一种基于 BM3D 算法的医学图像去噪与增强方法，为去除噪声和图像增强提供了全新的思路。

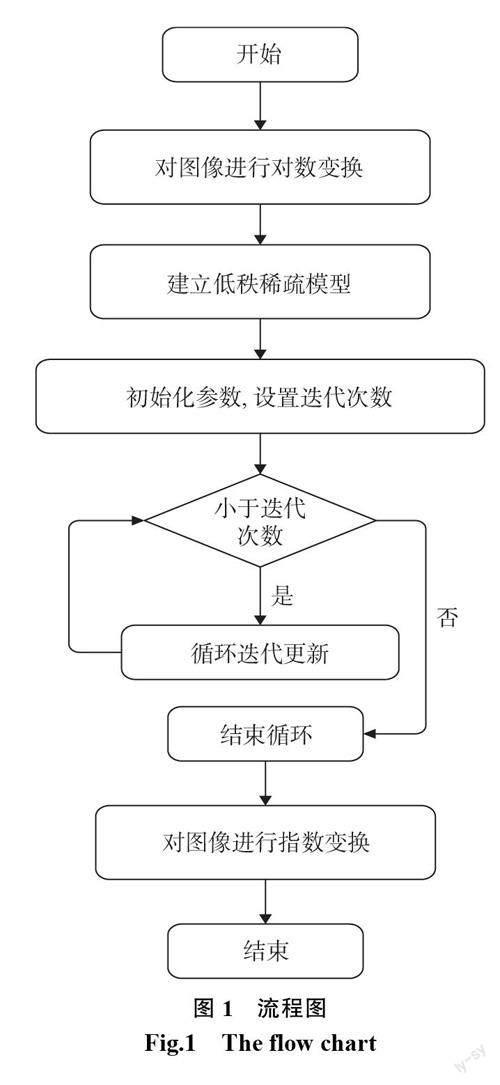
由于医学超声图像具有斑点噪声多[10]、纹理细节丰富[11]的特点，上述算法虽然在保持边缘和去噪方面有一定成效，但很难保留图像的纹理细节[12-13]。为解决上述问题，本文利用散斑噪声的乘性性质，通过对数变换将斑点噪声转换为加性噪声；分别利用图像和噪声的特性，将 L1范数和改进的低秩项作为正则项，以最小化保真项、正则项为目标函数，对图像迭代进行去噪估计，最后使用指数变换将结果图从对数域中还原，流程如图1所示。实验部分结合真实的消化道粘膜下肿瘤超声图像，对其添加斑点噪声和混合噪声后，与现有几种经典滤波算法进行对比实验。

1 研究方法

1.1 斑点噪声

超声内镜中的超声探头被安置在内镜前端，在进入消化道时进行实时扫描。由于人体的结构复杂和大量随机分布的散射粒子的存在，导致超声波在传播过程中发生干涉现象，因此在超声图像中形成了亮暗不定的斑点，这些斑点即为斑点噪声。

针对超声图像噪声， Jain 于1989年提出乘性和加性噪声组成的模型

式中： I、表示原始超声图像； R、和L、分别表示不含噪的图像和乘性噪声； N表示加性噪声；i和j为图像在空间域的局部坐标值。由于超声图像加性噪声的影响远小于乘性噪声，因此式（1）可写为

对两边取对数可得

进而得到斑点噪声图像近似的加性噪声模型

式中，I，R，L 分别为原始超声图像、不含噪图像和乘性噪声的对数表示形式。针对该加性噪声模型，建立低秩稀疏矩阵的分解模型，恢复出去噪后的图像，最后使用指数变换将结果图从对数域中还原。

1.2 稀疏模型

如果一个非零向量X中有少数几个非零元素，绝大多数元素为零，则称向量X具有稀疏特性。稀疏表示问题的目标即是寻找具有最少非零元素个数的解向量X*，数学上可表示为以下问题[14]：

式中：||x||0记为向量x 的 L0范数，表示向量x 中非零元素的个数； y 为已知向量；φ为给定参数。

以上优化求解是个 NP 难问题，在求解时通常会转而考虑计算近似解或者说次优解。故选择用其他的稀疏度量 L1范数取代非凸的 L0范数， 实现将以上优化问题凸松弛化，即

式中，||x||1记为向量x 的 L1范数，表示向量x 中所有元素的绝对值之和。

得到优化问题的解

1.3 低秩模型

低秩表示理论致力于求解所有数据向量联合后矩阵的最低秩表示。已有文献[15]证明绝大多数低秩矩阵可通过核范数约束来进行恢复，而加上保真项的低秩核范数约束问题又可以通过对奇异值矩阵软阈值操作来进行求解，这种核范数约束的表达式为

X（?）= argminX ||X 一 Y||F（2）+φ||X||*（8）

式中： Y 为已知矩阵；φ为平衡第一项数据保真项和第二项核范数约束项的参数。该式的解可通过下式得到

式中： U， V 是对 Y 的奇异值分解得到的，对 Y的奇异值分解为Y = UΣVT ；S φ（Σ）为对角阵Σ的软阈值算子，软阈值算子可表示为

式中， ii表示元素所在的位置。

但核范數也存在一些问题。为了保持模型的凸性，核范数约束将每个奇异值做了同等处理，即软阈值算子将每个奇异值均做相同数值的收缩。往往较大的奇异值通常表示想要保留的图像信息，不应过度惩罚；较小的奇异值通常表示想要去除的噪声信息，应予以惩罚。所以引入新的低秩约束矩阵[16]，定义为

式中，ε为一个非常小的正数。对数函数可以对奇异值进行收缩，这有利于保持更多有用的信息和消除噪声。

对以下低秩恢复问题

式中：α为权重参数。求解则有

2 基于低秩稀疏模型的去噪估计

本文引入了 L1范数和改进的低秩正则项，建立了稀疏低秩的加权范数约束模型[17]

式中：α ， β为权重参数。上式第一项控制数据的保真度，第二项约束稀疏噪声，第三项约束干净图像的低秩特性。

上述模型其求解问题可表示为

3 实验

为了验证本文提出的模型在超声内镜图像下抑制斑点噪声的有效性和鲁棒性，采用上海市第六人民医院所提供的消化道粘膜下肿瘤超声图片进行了实验。一共选取两幅图片：图像 a 为原始分辨率下的肿瘤超声图片；图像 b 为4张肿瘤超声图像缩小尺寸后拼接成的一幅图片。本实验使用的计算机主要配置如下：处理器为 AMD， R7-5800H，主频为3.20 GHz ，64位 Window11操作系统，实验所用软件为 R2016a 版本。由于现实中无法得到不存在噪声的理想图像，所以本文首先对得到的超声图像数据进行加噪处理[18]，加噪类型为斑点噪声和混合噪声，其中混合噪声为斑点噪声与高斯噪声混合，再利用本文模型与其他现有的经典去噪模型进行对比。

3.1 实验评价指标

为了客观地评价去噪算法，选择峰值信噪比（peak signal to noise ratio ， PSNR）、结构相似性（structural similarity ， SSIM）以及无参考锐化因子（cumulative probability of blur detection ， CPBD）这3种图像评判指标分别对不同滤波算法的去除噪声和结构信息、边缘保持能力进行量化对比。 SSIM[19]是一种结构一致性因子指标，建立在人眼的视觉特征基础上，用于衡量两幅图像的相似度，结果在0～1之间，其值越大，表明算法保存的组织结构信息越完整。 CPBD[20]是一种无参考图像锐化因子指标，可以反映出边缘和纹理细节的清晰度，其值越大，表明边缘和纹理区域越清晰。这里特别注意的是，我们想要达到的效果是图像在最大可能保持结构信息和纹理边缘细节的基础上去除噪声，所以优先关注 SSIM 和 CPBD。

3种量化指标公式分别如下：

3.2 实验结果

图2为加入斑点噪声后不同算法处理下的图像。其中，数字1为原图；2为斑点噪声；3为维纳滤波；4为引导滤波；5为 PM扩散滤波；6为 NLM 滤波；7为 BM3D滤波；8为本文算法。表2给出了加入半点噪声后各算法的结果比较。由表2数据可以看出，在加入斑点噪声的情况下，维纳滤波、 NLM 滤波、 BM3D 滤波的 PSNR 明显高于本文模型算法，针对维纳滤波和 BM3D 滤波，其 SSIM 和 CPBD 值均低于本文模型算法，这说明两种滤波在去除图像噪声的同时，不仅造成了图像组织结构信息的破坏，也使边缘和纹理区域变得模糊，这并不是我们想要的结果。针对 NLM 滤波，其 SSIM 值较高于本文模型算法，但 CPBD 较低于本文模型算法，就评价指标而言，算法在处理斑点噪声时表现良好，但值得注意的是， NLM 滤波算法的处理时间较长，为本文模型的数十倍甚至上百倍，无法满足快速去噪的特点[21]。针对 PSNR 较低于本文模型算法的 PM 扩散滤波，其 SSIM 和 CPBD 指标均不如本文模型算法。针对引导滤波，3种指标的表现和本文模型算法相差不大，处理时间也较快。

图3为加入混合噪声后不同算法处理下的图像，其中数字2为混合噪声，其他数字代表意义同图2。表3给出了加入混合噪声后各算法的结果比较。由表3数据可以看出，在加入混合噪声的情况下，维纳滤波、NLM 滤波、BM3D 滤波的 PSNR 明显高于本文算法，但3种滤波算法的 SSIM 和 CPBD 均低于本文算法，在去除图像噪声的同时，无法很好地满足结构信息和细节边缘的保存。针对 PSNR 较低或近似于本文算法的引导滤波和 PM 扩散滤波，其 SSIM 和 CPBD指标也均不如本文算法。

根据图4～6，经过对比可以发现，在加入斑点噪声时， NLM 滤波的表现最好，本文模型算法和引导滤波次之，两者不相上下。但是 NLM 滤波处理的时间较长，为引导滤波和本文算法处理时间的数十倍，甚至上百倍。在加入混合噪声时，本文算法的表现最好，在最大可能保持图像结构信息和边缘纹理细节的情况下，能够进行快速去噪。

综上所述，本文模型在处理斑点噪声和混合噪声时，在减少噪声影响的基础上，不仅能够很好地保存组织结构信息，减少边缘和纹理区域的模糊，还大大缩短了运算时间，能够满足实时性的特点。

4 结论

针对医学超声图像具有斑点噪声多、纹理细节丰富的特点，目前大多数去噪算法在保持边缘和去噪方面成效不错，但未能很好地保留图像的纹理细节。本文提出了一种改进的低秩稀疏矩阵分解模型，通过迭代的方式逐步消除超声图像中的噪声影响。实现了去除散斑噪声的同时保留纹理信息和边缘。本文根据上海市第六人民医院所提供的消化道粘膜下肿瘤超声图片进行实验，对医院提供的图片进行斑点噪声与混合噪声的合成，将本文模型与一些经典主流去噪模型进行对比，利用 PSNR ，SSIM ，CPBD 评价指标对去噪效果进行了评估，得出本文模型具备较好的 SSIM 和 CPDB。针对 SSIM，在处理斑点噪声时和混合噪声时，平均提高了18%和22%；针对 CPBD，在处理斑点噪声时和混合噪声时，平均提高了28%和26%，在处理速度上也能达到实时性的特点。表明本文算法不仅能快速地对含有斑点噪声或混合噪声的超声图像进行去噪，而且在定量评价指标表现上性能优良。综上所述，本文模型针对消化道粘膜下肿瘤超声图像的去噪估计具有良好的适用性和实时性。

参考文献：

[1]杨琴， 冶丽娜， 杨红伟.超声内镜在上消化道黏膜下病变诊治中的价值分析[J].中国实用医药 ， 2021， 16（30）：83–85.

[2] YUYJ，ACTONST. Specklereducinganisotropic diffusion[J]. IEEETransactionsonImageProcessing， 2002， 11（11）：1260–1270.

[3]晏满钰， 文成玉.改进的 PM 模型的医学超声图像去噪算法[J].成都信息工程大学学报， 2019， 34（6）：600–605.

[4]张聚， 王陈， 程芸.小波与双边滤波的医学超声图像去噪[J].中国图象图形学报， 2014， 19（1）：126–132.

[5] ZHOUXM，LIUW，ZHANGCY，etal. Speckle reduction of ultrasound elastography with bilateral filter[J]. Advanced Science Letters， 2013， 19（10）：3025–3027.

[6] RAHIMIZADEHN，HASANZADEHRP，JANABI- SHARIFI F. An optimized non-local LMMSE approach for speckle noise reduction of medical ultrasound images[J]. MultimediaToolsandApplications，2021，80（6）：9231–9253.

[7]陈晓冬， 吉佳瑞， 盛婧， 等.分数阶微分加权引导滤波对超声图像的纹理保持[J].光学精密工程， 2020， 28（1）：174–181.

[8]薛双青， 贺东东.基于2D-VMD 和双边滤波的医学超声图像去噪算法[J].西安科技大学学报 ， 2021， 41（3）：516–523.

[9]张光华， 潘婧， 邢昌元.基于 BM3D 算法的醫学图像去噪与增强方法研究[J].电脑知识与技术， 2019， 15（18）：223.

[10] UDDINMS，TAHTALIM，LAMBERTAJ，etal.Speckle-reductionalgorithmforultrasoundimagesin complexwaveletdomainusinggeneticalgorithm-based mixturemodel[J].AppliedOptics，2016，55（15）：4024–4035.

[11] KHAN A H， AL-ASAD J， LATIF G. Speckle suppression inmedicalultrasoundimagesthroughSchur decomposition[J]. IETImageProcessing， 2018， 12（3）：307–313.

[12] ADAMOF，ANDRIAG，ATTIVISSIMOF，etal. A comparativestudyonmotherwaveletselectionin ultrasound image denoising[J]. Measurement， 2013， 46（8）：2447–2456.

[13] BONNY S， CHANU Y J， SINGH K M. Speckle reduction of ultrasound medical images using Bhattacharyya distanceinmodifiednon-localmeanfilter[J]. Signal，Imageand Video Processing， 2019， 13（2）：299–305.

[14]沈晓东.基于结构性稀疏优化的 SAR 图像斑点噪声抑制[D].重庆：重庆大学， 2018.

[15] CAND?SEJ，RECHTB. Exactmatrixcompletionvia convexoptimization[J]. FoundationsofComputational Mathematics， 2009， 9（6）：717–772.

[16] DIAN R W， LI S T， FANG L Y. Learning a low tensor- trainrankrepresentationforhyperspectralimagesuper- resolution[J]. IEEE Transactions on Neural Networks and Learning Systems， 2019， 30（9）：2672–2683.

[17]杨垚， 黄聪， 王华军.基于低秩和稀疏模型的高光谱图像快速去噪方法[J].物探化探计算技术 ， 2021， 43（5）：663–668.

[18] MAFIM，TABARESTANIS，CABRERIZOM，etal. Denoisingofultrasoundimagesaffectedbycombined speckleandGaussiannoise[J]. IETImageProcessing， 2018， 12（12）：2346–2351.

[19] HOR?A，ZIOUD. Imagequalitymetrics： PSNRvs. SSIM[C]//Proceedings of the 20th International Conference onPatternRecognition. Istanbul，Turkey： IEEE， 2010：2366–2369.

[20] NARVEKAR N D， KARAM L J. A no-reference image blurmetricbasedonthecumulativeprobabilityof blur detection（CPBD）[J].IEEETransactionsonImage Processing， 2011， 20（9）：2678–2683.

[21] DE FONTES F P X， BARROSO G A， COUP? P， et al. Real time ultrasound image denoising[J]. Journal of Real- Time Image Processing， 2011， 6（1）：15–22.

（編辑：董伟）