复杂环境下的稳健广义旁瓣相消技术
雷圆圆 刘 冰
(西安电子工程研究所 西安 710100)
0 引言
在复杂的电磁环境中,雷达探测面临愈来愈多的挑战。一方面,多径效应所产生的强相干干扰信号以及其他非相干干扰导致传统的自适应波束形成算法性能迅速下降甚至失效[1];另一方面,由于传统广义旁瓣相消算法(Generalized Sidelobe Canceller,GSC)在实际环境中对小快拍数、较强的期望信号功率以及角度失配敏感,导致其性能下降[2],甚至可能在期望信号方向形成零陷,严重恶化了输出信干噪比(Signal to Interference plus Noise Ratio, SINR)。因此,对复杂环境下GSC算法稳健性的研究是十分必要的。
目前国内外已提出大量针对相干信号的处理算法,主要可以分为两大类:降维处理和非降维处理,其中降维处理算法又包括基于空间平滑[3-4]与基于矩阵重构[5]两大类,空间平滑类算法通过牺牲孔径的方式进行相干信源协方差矩阵的解相干,但其在低信噪比情况下性能受限;矩阵重构类算法通过对信号子空间特征矢量、数据接收协方差矩阵以及接收相关矩阵进行某种重排,从而实现满秩矩阵恢复。非降维处理算法包括频域平滑法、虚拟阵列变换法、Toeplitz方法等,与降维处理算法相比,此类算法不会带来阵列孔径的损失,其中传统Toeplitz算法通过求解整个接收数据协方差矩阵恢复Toeplitz性质,但其特征值分解后的小特征值不一定相等,会造成方向图和功率谱的误差与失真。
为了提高自适应波束形成器的稳健性,又相继出现了对角加载技术[6]、特征子空间投影技术[7]以及协方差矩阵重构技术[8]等,其中对角加载技术简单有效,它使得采样协方差矩阵的小特征值散步程度变低,但其提升性能有限,并且最优加载量选取困难;基于特征空间的波束形成算法通过将权值向对应子空间投影,不仅解决了期望信号相消的问题,同时也缓解了导向矢量失配,但当接收信噪比较低时,由于子空间混叠纠缠的影响,导致波束形成器性能下降。基于协方差矩阵重构算法通过预设零陷的范围,将干扰加噪声的协方差矩阵进行积分重构,进行零陷展宽从而提高稳健性。
针对复杂环境下传统GSC算法性能受限问题,本文提出了一种适用于复杂环境的波束域稳健GSC算法,通过利用修正Toeplitz算法(Modify Toeplitz,MTOP)对接收数据协方差矩阵进行解相干预处理,构造转换矩阵并将阵元域接收数据转至波束域,从而实现矩阵降维并提高系统稳健性,之后建立了针对较强信号功率以及角度失配的稳健GSC框架,进一步提高了算法的稳健性。
1 信号模型
本文采用阵元数为N,阵元间距d=λ/2的均匀线阵作为接收阵列,在处理时间t内的接收信号可以表示为
(1)
其中:s0(t)和a(θ0)为期望信号复合包络和导向矢量;sl(t)和a(θl),l=1,2,…,L为期望信号多径复合包络和导向矢量;sl(t)=βls0(t),βl为第l个多径相干信号sl(t)相对于期望信号s0(t)的衰落因子;gp(t)和a(θp),p=0,1,2,…,P为非相干干扰信号复合包络和其导向矢量。阵列接收信号的协方差矩阵Rx可以表示为
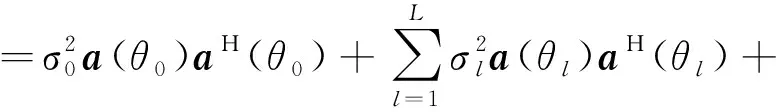
(2)
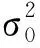
(3)
2 传统GSC算法
传统GSC算法是线性约束最小方差(Linearly Constrained Minimum Variance,LCMV)算法的另一种无约束实现方式,由静态权值的非自适应支路和与接收数据相关的自适应支路构成,其结构如图1所示。
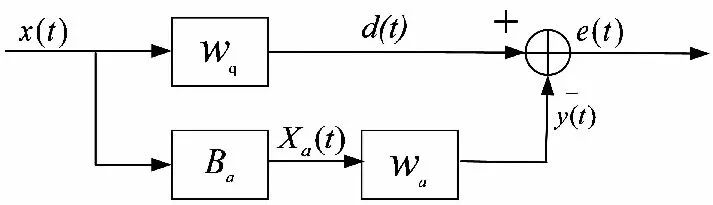
图1 传统GSC结构
基于LCMV准则,系统权向量w可表示为
(4)
令R为接收信号的自相关矩阵,C为M×(J+1)维约束矩阵,f为(J+1)维约束向量,M为阵列天线数,J为干扰信号个数,则式(4)的最优解可以表示为
w=R-1C(CHR-1C)-1f
(5)
在与LCMV等效的广义旁瓣相消器结构中,权向量被分解为自适应和非自适应两部分,其中非自适应部分位于约束子空间中,自适应部分正交于约束子空间,则系统权向量w可表示为
w=wq-Bwa
(6)
其中
wq=(CCH)-1Cf
(7)
wa=(BHRB)-1BHRwq
(8)
B为M×(M-J-1)维阻塞矩阵,通过将期望信号阻塞掉使之不进入辅助支路,组成B的列向量位于约束子空间的正交互补空间中,并满足BHC=0。
传统的GSC框架在较强信号功率以及角度失配的影响下,接收信号在经过阻塞矩阵BT后,残留的期望信号会被当作干扰进行处理,严重时会导致信号相消。因此,下支路的阻塞矩阵构造以及自适应权值的求取对系统性能影响至关重要。
3 波束域稳健GSC算法
针对在复杂环境下传统GSC算法性能下降且稳健性差的问题,本文首先对接收数据协方差矩阵进行MTOP矩阵重构,然后构造转换矩阵T将阵元域接收数据转至波束域,最后结合特征空间的思想建立基于联合权矢量的稳健GSC框架,提高算法稳健性。本文波束域稳健GSC算法结构如图2所示。
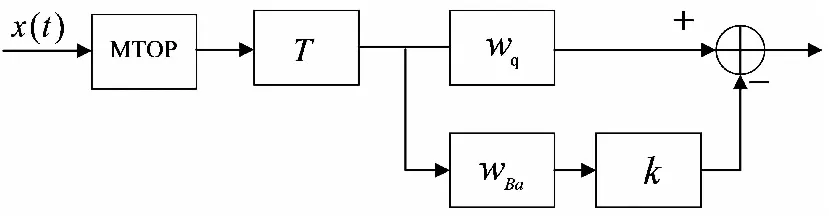
图2 波束域稳健GSC算法结构
1)MTOP矩阵重构
利用采样数据中的第一行元素与第n行元素的互相关函数进行协方差矩阵重构,其互相关函数可以表示为
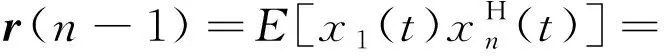
(9)
其中,A(n)为阵列导向矢量的第n行元素,则数据矢量r可以表示为
r=[r(0),r(1),…,r(N-1)]
=A(1)R[AH(1),AH(2),…,AH(N)]
(10)
式(10)包含接收数据的所有信息,分别定义矩阵R1和矩阵R2为
(11)
(12)
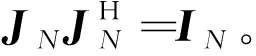
RMTOP=(R1+R2)/2
(13)
经过重构的协方差矩阵RMTOP具有Toeplitz性质,在不牺牲阵列孔径的前提下有效消除了信号之间的相关性,MTOP相比于传统的TOP算法复杂度由O(N2)下降至O(N),并且具有更强的干扰抑制能力,有效避免了方向图和功率谱的误差和失真问题。
2)波束域转换
基于均匀线阵,假设N/B为正整数,v=[1,1,…,1]T为(N/B)×1的列向量,则转换矩阵T可以表示为
(14)
通过变换将整个阵列分解为B个子阵,每个子阵的阵元数为N/B,并且矩阵T满足正交特性,即TTH=I。
利用转换矩阵T将阵元域接收信号协方差矩阵转换到波束域,即:
RB=THRMTOPT
(15)
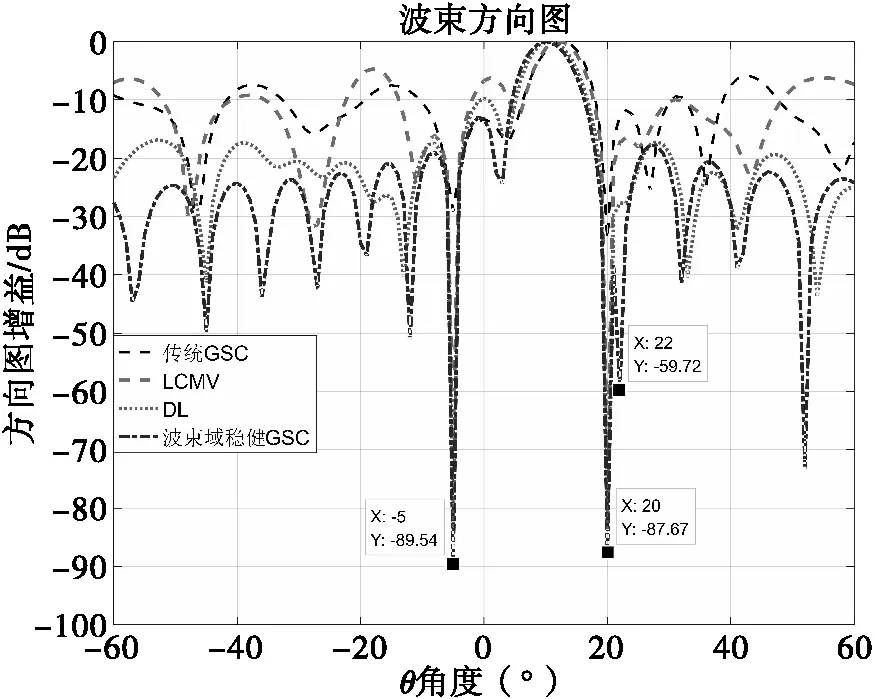
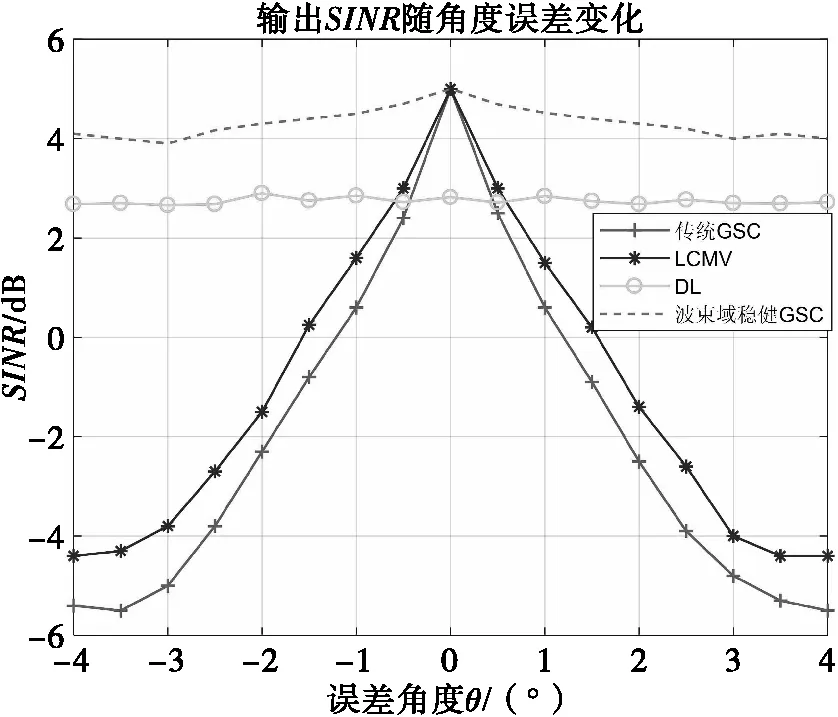
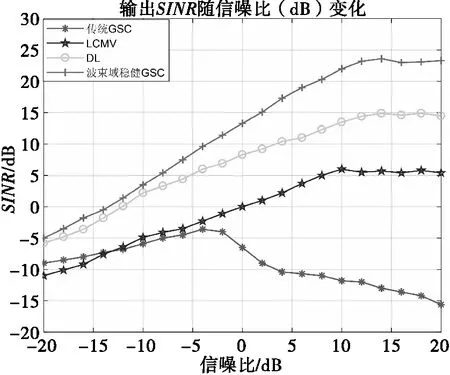
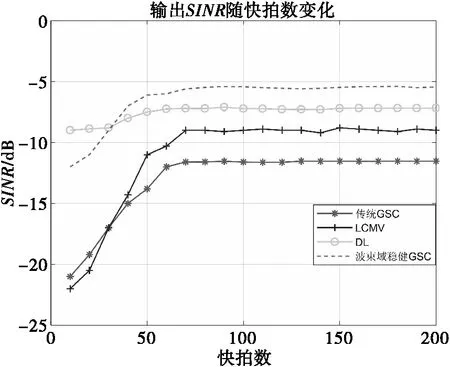
其中,转换矩阵T为N×P维矩阵,P为形成波束数目,且P 相应的,波束域对应的主支路静态权值aT为 aT=THwq (16) 3)联合权矢量的稳健GSC框架 本文考虑对BT和waT的取值形成联合加权矢量wBa,然后结合特征空间的思想将求得的权矢量wBa向大特征值对应的信号子空间投影,可在角度失配的情况下避免角度失配引起的导向矢量失配和协方差矩阵误差,提高GSC框架稳健性。 针对信号子空间的求解,本文通过波束域协方差矩阵逆的高次幂近似等效信号子空间,有效避免了矩阵分解带来的大运算量。波束域协方差矩阵RB经特征值分解后得到噪声子空间EN和信号子空间ES为 (17) 其中:λi为特征值;ei为特征值对应的特征向量;ES为L+P+1个较大特征值对应的信号加干扰子空间;EN为N个小特征值对应的噪声子空间,对式(17)变形可得: (18) (19) 由于信号子空间正交于噪声子空间,则信号子空间可表示为 (20) 本文基于最小化输出功率准则,结合特征子空间投影建立最差性能条件下的最优权值稳健GSC框架的目标函数及约束条件,得到联合权矢量wBa的约束条件为如式(21)所示。 (21) 式(21)可化简为 (22) 以上约束条件选取为一个凸优化方程,采用内点法进行求解,并选定适宜的约束参数ε=10-4,e=5,使用Matlab软件工具包CVX进行求解得到wBa,进而得到波束域稳健框架下的算法权值为 wBJWV=wq-wBa (23) 波束域稳健GSC算法实现步骤如表1所示。 表1 波束域稳健GSC算法实现步骤 通过仿真分析传统GSC、LCMV算法、DL算法与本文所提波束域稳健GSC算法在不同条件下的波束形成性能,仿真条件:以16阵元的均匀线阵作为接收阵列,接收信号包含入射角度为10°的期望信号,入射角度为22°的相干干扰,从-5°,20°入射至阵列的两个非相干干扰以及独立分布的高斯白噪声信号。 1)阵列方向图 假设期望信号存在角度失配为3°,SNR为10dB,快拍数为100,传统GSC、LCMV算法、DL算法和本文所提出的波束域稳健GSC算法的方向图如图3所示。 图3 阵列方向图 图4 角度失配条件下输出SINR 图5 不同SNR条件下的输出SINR 图6 不同快拍数条件下的输出SINR 受相干信源和角度失配的影响,传统GSC算法和LCMV算法产生主瓣偏移,对干扰信号生成零陷较浅,干扰抑制能力几乎失效;DL算法可以在导向矢量失配条件下有效改善波束形成得性能,并且能够在期望信号形成增益且在干扰方向生成零陷;本文所提出的波束域稳健GSC算法能够准确在期望信号方向形成增益,在干扰方向形成深零陷,且该算法相对于DL算法的副瓣更低,对干扰具有更强的抑制能力。 2)角度失配条件下的输出SINR 假设期望信号存在的失配角度范围为-3°~3°,SNR为-10dB,快拍数为100,进行100次蒙特卡洛仿真,比较传统GSC算法、LCMV算法、DL算法以及本文所提出的波束域稳健GSC算法输出SINR随角度失配程度的变化情况。 由仿真结果可以看出,各算法在0°都可以得到良好的性能。随着角度失配程度的增大,传统GSC算法和LCMV算法输出SINR明显下降,原因是由于算法对导向矢量失配和协方差矩阵的误差较为敏感;对角加载算法针对角度失配问题对接数据协方差矩阵进行了重构,其输出SINR基本保持稳定;本文所提出的波束域稳健GSC算法在角度失配情况下输出SINR稳定且输出SINR高于DL算法,具有稳健性。 3)不同SNR条件下的输出SINR 假设期望信号存在角度失配为3°,快拍数为100,进行100次蒙特卡洛仿真,比较传统GSC算法、LCMV算法、DL算法以及本文所提出的波束域稳健GSC算法输出SINR随SNR的变化情况。 由仿真结果可以看出,本文所提出的波束域稳健GSC算法在角度失配的情况下,在低信噪比和高信噪比下均能保持较高的输出SINR,这是由于算法针对角度失配进行了联合权值的求解,可以在误差存在的环境下保持良好性能。传统GSC算法在低信噪比时,其性能较优,随着信噪比的增大以及角度失配的影响,容易产生信号相消现象,导致输出SINR严重下降。LCMV算法和DL算法随着信噪比的增加,其输出SINR随之增加,LCMV算法总体性能不及DL算法。 4)不同快拍数条件下的输出SINR 假设期望信号存在角度失配角度为3°,SNR为-20dB,快拍数从0变化到100,进行100次蒙特卡洛仿真,比较传统GSC算法、LCMV算法、DL算法以及本文所提出的波束域稳健GSC算法输出SINR随快拍数的变化情况。 由仿真结果可以看出,本文所提出的波束域稳健GSC算法不仅可以快速收敛,而且稳定后的输出SINR明显优于传统GSC算法。DL算法的性能优于传统GSC算法和LCMV算法,LCMV算法在低信噪比时性能较差,即使在快拍数增加的情况下,由于对失配误差敏感,导致其性能远不及波束域稳健GSC算法。 在多径效应、非相干干扰以及噪声并存的复杂环境下,针对传统的自适应波束形成算法性能受限、快拍数受限以及算法对角度失配敏感等问题,本文提出一种复杂环境下的波束域稳健GSC算法,所提算法在存在相干信源和角度失配情况下能够准确在期望信号方向形成增益,在干扰方向形成较深零陷,且具有更低的旁瓣,对干扰具有更强的抑制能力。通过仿真分析,所提算法的输出SINR在角度失配、不同快拍数以及不同输入SNR的条件下均可以保持良好输出,具有较高的稳健性。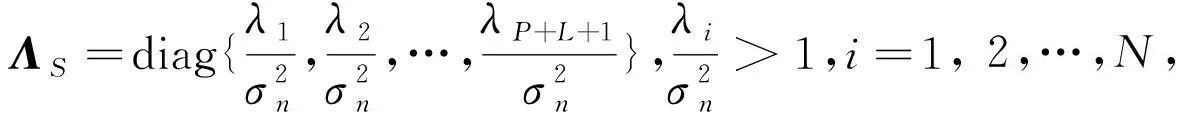
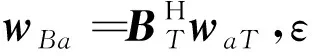

4 仿真分析
5 结束语

