基于相位编码信号的多目标参数测量方法

张孟达 余颖菲

(1.中国电子科技集团公司第三十八研究所 合肥 230031;2.孔径阵列与空间探测安徽重点实验室 合肥 230031)

0 引言

跟踪雷达常采用线性调频信号探测目标[1]。相对于其它信号,线性调频信号具有容易产生和方便处理等优点。但是线性调频信号经过脉冲压缩后会产生距离多普勒耦合[2],使得距离量测有一定偏差(偏差和径向速度及耦合系数有关),必须经过速度补偿才能估计出准确的距离[3]。常用的一种补偿方法为根据点航处理的预测速度进行补偿。该方法需要目标进入稳定跟踪后才能使用,且在多目标场景下,不同目标需要匹配不同的速度,会给软件处理带来很大的困难。另一种方法为发射信号采用正负调频斜率脉冲信号,回波信号经过脉冲压缩处理后得到未修正的距离测量值,根据正负调频信号脉冲压缩距离走动误差大小相等且正负相反的特性得到真实目标距离值,从而实现对目标的参数估计。这种方法实现简单,但在多目标时需要对正负线性调频信号进行配对使用。文献[4]提出一种多调频斜率合成的脉冲信号,根据距离-多普勒耦合偏差的计算公式建立方程组,利用逐次筛选方法识别真实目标,得到多目标环境下脉冲信号对目标参数估计。该方法的缺点为当目标数目较多时性能下降,算法复杂度提高。对于多目标场景,跟踪雷达还可以采用相位编码信号进行目标探测,由于相位编码信号对多普勒敏感,也需要对多普勒进行补偿[5-6],常用的补偿方法通常运算量较大,不易工程实现。

本文提出一种新的相位编码信号处理方法。该方法优选波形(采用legendre序列产生二相编码信号)以及改进处理方式达到了较好的处理效果。具体方法为按照与发射波形反相的相位编码信号进行补偿,补偿后的信号再进行FFT处理。在由距离滑窗和FFT构成的距离-多普勒二维空间进行目标检测即可同时估计出多目标的距离和速度。仿真结果表明该方法有效可行,测量精度满足要求。

1 相位编码信号

相位编码信号是由多个子脉冲构成,子脉冲的宽度相等且具有特定的相位,这些特定的相位是由给定的伪随机编码序列确定的。同时,相位调制函数具有离散的有限状态,即相位编码属于离散编码脉冲压缩信号,故相位编码信号被称为伪随机编码信号。基带相位编码信号复数形式可以表示为

S(t)=a(t)ejφ(t)

(1)

其中,φ(t)为调制函数,a(t)为幅度调制,对于矩形脉冲调制

(2)

其中,τ为码元宽度,N为码元个数。

相位编码信号可分为二相码和多相码,雷达中常用的二相编码信号有巴克码、m序列码等。

普通的相位编码信号,脉冲压缩后副瓣较高,需要采用失配滤波降低脉压副瓣。为了避免脉压副瓣过高造成多目标之间相互影响,必须寻找自相关特性好的编码波形。本文采用legendre序列作为二相编码信号,相比m序列码,有更好的自相关特性。

legendre序列是一种基于二次剩余理论提出的二元伪随机序列,其定义如下[7]:

序列的周期p为任意素数,gcd(P,i)=1,legendre序列的元素:

(3)

对于周期为奇素数p的legendre序列,若P≡m(mod4),则其自相关函数[8]:

(4)

当P≡3(mod4)时,legendre序列的自相关函数取值只有两种,此时称legendre序列为二值自相关序列。二值自相关序列具有较好的自相关特性,可利用此序列设计雷达信号。假设雷达采样频率为5MHz,码元宽度0.2μs,脉冲宽度1ms,则脉宽内的采样点数为5000。P为5000内最大的素数,且满足P≡3(mod4),经过计算P取4999满足要求。周期为4999的legendre序列自相关函数如图1所示。

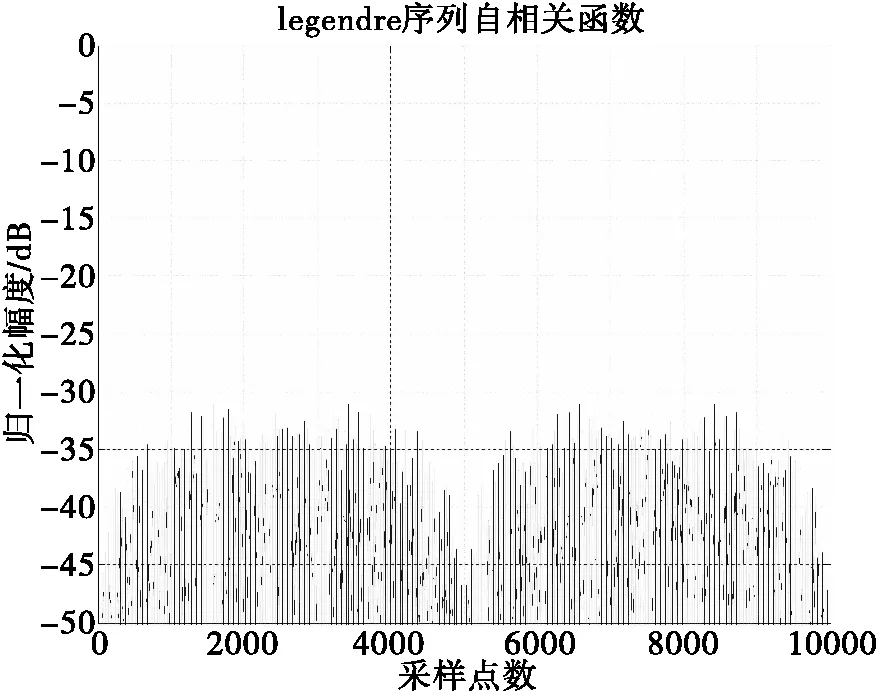
图1 legendre序列自相关函数

可以看出,采用legendre序列的二相编码信号具有较好的自相关特性,副瓣可以到30dB以下。

2 多目标模型

雷达多目标跟踪的示意图如图2所示。

图2 雷达多目标跟踪示意图

雷达发射信号采用由式(1)表示的采用编码信号,则多目标回波信号可以表示为

(5)

其中:N表示目标个数;Ai表示第i个目标的回波幅度;fdi表示第i个目标的多普勒频率;τi表示第i个目标的距离所对应的延时。

3 距离-多普勒处理

常规的处理方法是先对多目标回波进行脉冲压缩,再对脉压后的数据进行慢时间维多普勒滤波。由于相位编码信号对多普勒敏感,会造成脉冲压缩的失配,必须对每个目标的多普勒进行补偿[9]。在目标的速度未知时,只能在一定范围里搜索。该方法的缺点是当多目标之间的速度相差较大时,多普勒补偿的搜索范围太大,造成运算量巨大,不能满足实时处理的需求。本文针对多目标跟踪的典型应用场景(距离有引导信息且距离相差不大,速度信息未知),提出一种在距离上进行滑窗处理的方法,可有效减少运算量,并且多普勒估计精度较高。该方法的原理如下:选取和发射波形相位相反的参考信号为

Sf(t)=e-jφ(t)

(6)

将该参考信号在时域滑窗后和回波信号相乘,相当于在距离维搜索。当滑窗的位置恰好和第i个目标对应的延时τi重合时,相乘后的信号可以表示为

Aia(t-τi)ej2πfdi(t-τi)

(7)

可以看出,该信号在矩形窗a(t-τi)内为单点频信号,此时只需要做FFT即可得到第i个目标的多普勒频率。因此,处理流程可按以下步骤进行:

1)第一步:根据引导信息确定目标回波距离开窗起始位置以及开窗时长L,并根据采样频率fs计算开窗点数N,N=floor(fsL);

2)第二步:将回波信号在0～N-1范围内按照采样点依次滑窗,滑窗后的回波信号和参考信号相乘并做FFT,FFT点数为M,M=2ceil(log2N);

3)第三步:将N次滑窗的FFT结果排成一个N×M的二维矩阵,并做两维CFAR检测;

4)第四步:假设第i个目标的过门限信号的下标为(ni,mi),根据该下标可以计算出该目标的距离和多普勒。

可以看出,对于普通二相编码信号,上述方法依然适用,但是采用legendre序列作为二相编码信号,距离-多普勒两维处理后距离副瓣较低,有更好的多目标检测性能。

对于相位编码信号,采样间隔必须为码元宽度的整数倍,本文采用一个码元宽度,对应的距离分辨率为ΔR=Cτ/2,其中,C为光速,τ为码元宽度。由于采用距离滑窗处理,则测距误差范围在-ΔR/2～ΔR/2以内。因此距离均方根误差可以表示为

δR=ΔR/4

(8)

测速误差和多普勒分辨率相关,假设积累时长为T,对于单脉冲测速,T=Nτ,则多普勒分辨率为

Δf=1/(Nτ)

(9)

若直接采用多普勒频道选大方法,多普勒均方根误差为Δf/4。采用文献[10]所用的三滤波器比幅方法测速,可以有效提高测速精度。该测速方法的多普勒均方根误差可以表示为

(10)

其中Kd为多普勒误差斜率,和多普勒滤波器组的间隔及响应曲线有关,一般取1.2～1.4之间,SNR表示信噪比。

传统的距离-多普勒处理方法在频域滑窗,按照每个频点进行多普勒补偿后再做频域脉压。假设传统方法频域滑窗点数为N1,脉压点数为M,本文方法距离滑窗点数为N2,FFT点数为M。则两种方法运算量运算量对比如表1所示。

表1 运算量对比

可以看出,当N1和N2相当时,本文方法的运算量小于传统方法的一半。实际处理过程中由于有距离引导信息,且距离开窗较小,因此N2远小于N1,本文方法运算量显著降低。

4 仿真结果分析

构建如下多目标场景,雷达接收引导信息,按照引导点位打跟踪波束。被探测多目标在波束宽度内,多目标个数为5个,5个目标距离和速度均不相同,距离和速度随时间的分布分别如图3和图4所示。

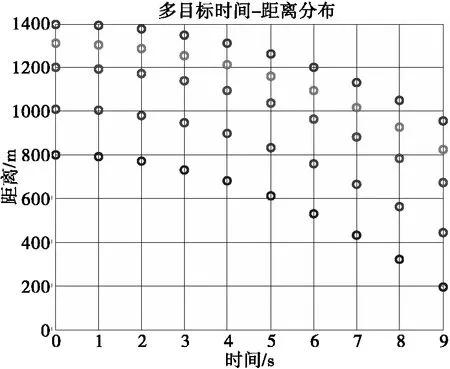
图3 多目标距离分布

图4 多目标速度分布

其中,目标距离为相对于开窗前沿的距离。雷达发射基于legendre序列的二相编码信号,采用1Hz数据率跟踪,共仿真10帧数据。采用本文的处理方法,其中一帧数据的距离-多普勒处理结果如图5所示。

图5 距离多普勒处理结果

目标检测结果如图6所示,可以看出在距离-多普勒二维平面,5个目标同时被检出。对于脉冲宽度为1ms的单脉冲信号,在信噪比16dB条件下,对于多帧数据和多个目标进行200次蒙特卡洛试验,测距一次差和测速一次差分别如图7和图8所示。

图6 二维检测输出

图7 测距误差

图8 测速误差

统计得到的测距均方根误差为8.48m,测速均方根误差为2.92m/s,经过和公式(8)和公式(10)对比,可以得出测距误差和测速误差与理论分析一致,证明了该检测方法的可行性。

5 结束语

对于跟踪雷达,在多目标场景下,如何同时估计出目标距离和速度是一个技术难点。若采用线性调频信号,由于存在距离多普勒耦合,多目标速度估计和补偿比较困难,且多目标的速度需要匹配。本文采用基于legendre序列的二相编码信号,提出在距离维滑窗处理的新方法,可同时估计多目标距离、速度。该方法避免了频域搜索,有效降低运算量,可并行处理,易于工程实现。