基于宽度学习的微多普勒目标分类

李晓斌 袁子乔 徐 飞 刘 畅

(西安电子工程研究所 西安 710100)

0 引言

随着智能化信息技术发展的不断深入,针对于窄带雷达的空中目标识别技术研究受到广泛关注,越来越需要窄带防空雷达在具备发现目标的同时进行目标属性自动分类的能力。近年来,微动特性在雷达目标探测与识别中受到广泛关注,微动是指雷达目标除质心平动以外的振动或转动,由微动产生的多普勒频率为微多普勒频率。不同的微动会产生不同的微多普勒,微多普勒效应可以反映目标结构部件的几何构成和运动特性,是目标本质的特征。基于目标微动差异可以提取具有良好分类性能的特征,从而实现对目标的分类和识别。

传统特征提取方法[2]需要更多的人工操作,不仅耗费时间和精力,且因为人工经验抽取信号特征是随机过程,会带来相应的误差。随着人工智能的崛起,基于大数据和深度学习[1]的分类识别方法越来越多,相比于传统的利用波形熵、二阶中心矩等特征,利用支持向量机、决策树作为分类器来实现微多普勒分类的方法,由于能够提取到识别对象中更深层次的信息特征,所以它的分类效果会更好。但是深层结构的神经网络并不是完美无缺,它的网络结构复杂,需要对很多的超参数进行设置。它需要不断地进行多次迭代,求取层与层之间的连接权重,并且需要反向调节网络的权重,才能够得到较好的分类结果。此外,当模型训练好之后,就不能再对训练数据进行更新。若更新训练数据,那么就需要将整个深层神经网络再次训练,给用户造成了很多不便。

宽度学习(Broad Learning System,BLS)系统[3-6]相较于深层神经网络,网络结构简单,只有输入层和输出层两层,不需要通过多层的隐藏层来提取识别对象的特征,并且省去了不断更新层与层之间连接权重的过程,计算量变小,所以它的训练速度非常迅速,训练时间减少了成百上千倍。此外,当训练数据发生更新时,它不需要重新训练整个网络,而只是通过BLS的增量学习算法就可以达到重建网络,这极大地提升了用户的体验感。因此,考虑将宽度学习算法应用到雷达的目标分类识别,探索其可行性。

1 宽度学习系统

宽度学习的前身是随机向量函数连接网络(Random Vector Functional Link Neural Network,RVFLNN)[7],如图1所示。

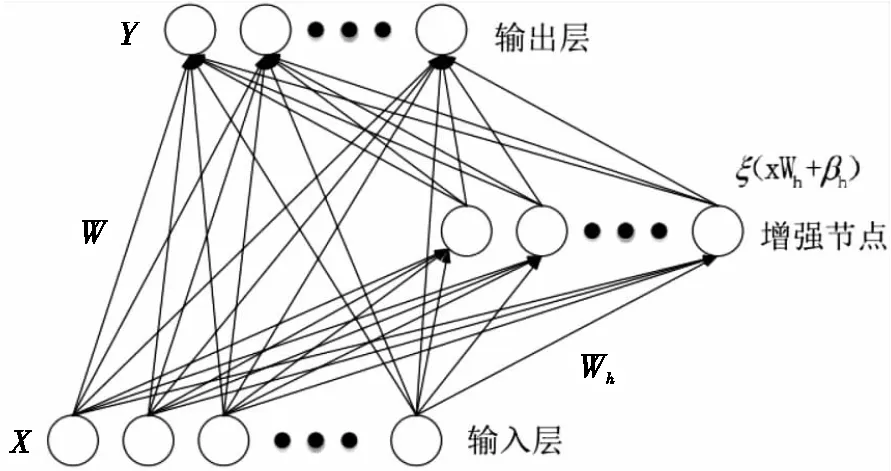
图1 RVFLNN的网络结构

这种网络结构由输入层、隐藏层和输出层3部分组成,输入层除了与隐藏层相连接之外,还直接和输出层进行了连接。这个网络结构通过不断更新输入层与输出层之间的连接权重W和输入层与隐藏层之间的连接权重Wh而取得较好的分类效果。其中,X为输入数据,Y为输出的分类结果,输入数据X经过非线性变换ξ(xWh+βh)得到增强节点的值。此外,输入层和输出层、隐藏层与输出层都是仅有线性变换。

宽度学习系统的网络结构如图2所示,可以看到,宽度学习系统相较于RVFLNN,只是由输入层和输出层组成,但是输入层发生了变化。首先,输入数据X经过线性变换成为多个特征节点Z1,Z2,…,Zn,增强节点H1,H2,…,Hn则由特征节点经过非线性变换映射得到。特征节点和增强节点共同构成了输入层,并且与输出层Y直接连接。其中φ为激活函数,常用的激活函数有tanh、sigmoid等。W为网络的权重,β为网络的偏置,它们都是随机生成的。

图2 宽度学习系统网络结构图

1.1 特征节点

特征节点Z是输入数据X经过线性变换映射得到的,映射函数为φ(XWe+βe)。则生成第i个特征节点Zi为

Zi=φ(XWei+βei)

(1)

其中,βei为偏置项,Wei为随机生成的权重,优化目标函数为

(2)

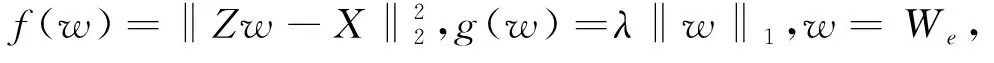
(3)

ρ>0,S为软阈值算子,定义为

(4)

特征层可以定义为Zn=[Z1,…,Zn]。

1.2 增强节点

增强节点是由特征节点经过非线性变换映射得到的,映射函数为ζj(ZjWhj+βhj),它能够进一步提取输入信号的深层次特征,得到增强节点的表达式为

Hm≡ζ(ZnWhm+βhm)

(5)

其中Whj为特征节点到增强节点的权重,βhj为偏置项。由于整个过程都是非线性变换,所以需要使用激活函数对增强节点进行激活,而映射函数ζj(ZjWhj+βhj)中已经完成了该步骤,故本文不再介绍。

增强层可以定义为Hm≡[H1,…,Hm]。

1.3 伪逆运算

根据上述介绍,宽度学习的输入数据为X,输出结果为Y,输入层与输出层的连接权重为W,则网络的数学模型为Y=WX,由于宽度学习是一种有监督的网络模型,故输入数据X和输出结果Y是已知的,只需要求解连接权重W即可。宽度学习使用了岭回归方法对连接权重W进行求解。宽度学习网络的数学模型为

Y=[Z1,…,Zn∣ξ(ZnWh1+βh1),…,ξ(ZnWhm+βhm)]W

=[Z1,…,Zn∣H1,…,Hm]W

=[Zn∣Hm]W

(6)

其中,Zn为输入层的所有特征节点,Hm为输入层的所有增强节点,将Zn和Hm组合在一起作为输入X。求解连接权重W就是对式(6)进行逆运算W=[Zn∣Hm]+Y。逆运算求解时,由于输入并不规则,所以求解并不是非常容易。宽度学习系统是通过伪逆进行求解,连接权重W求解公式为

W=(VTV+In+mc)-1VTY

(7)

其中,V为Zn和Hm的组合,n和m代表两种节点的数量,它们并不是固定值,需要实验者根据数据集的大小进行设定。

因此,输入数据A的伪逆为

(8)

其中:c为正则化参数。

2 BLS的增量学习算法

当特征节点、增强节点和样本数据发生变化时,宽度学习系统相较于传统的机器学习算法或者深层神经网络,它的特点在于并不需要重新训练整个网络。只需要使用增量学习算法就可以重建模型,接下来,本文将分别进行阐述。

2.1 增加增强节点

增强节点的作用在于能够将信号信息中的深层次特征提取出来,所以增强节点的增多可以提高分类精度。

现有的输入层为V=[Zn∣Hm],添加p个增强节点后为

Vm+1≡[Vm∣ζ(ZnWhm+1+βhm+1)]

(9)

其中Whm+1∈Rnk×p,是映射p个增强节点的特征节点权重系数,βhm+1∈Rp是偏置项。

得到Vm+1的伪逆是:

(10)

令D=(Vm)+ζ(ZnWhm+1+βhm+1),C=ζ(ZnWhm+1+βhm+1)-VmD,则BT为

(11)

更新后的权重是:

(12)

BLS的增加增强节点算法如图3所示。

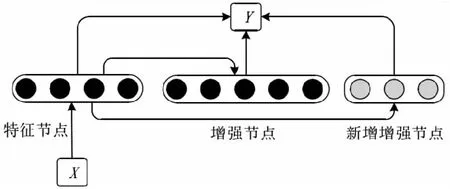
图3 BLS的增加增强节点算法

2.2 增加特征节点

特征节点的个数也会影响到分类精度,特征节点个数过少,会导致从输入数据中提取的特征并不充分,即使增强节点再多,也并不能提高分类精度,所以常常需要增加特征节点来达到预期的效果。

假设增加第n+1个特征节点,表达式为

Zn+1=φ(XWen+1+βen+1)

(13)

所对应的增强节点则为

Hexm=[ζ(Zn+1Wex1+βex1),…,ζ(Zn+1Wexm+βexm)]

(14)

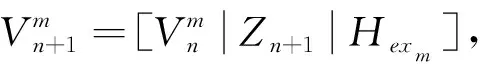
(15)

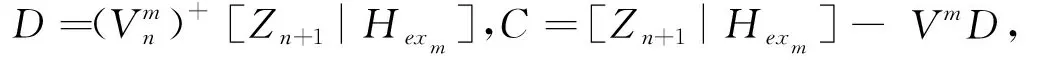
(16)

得到新的权重:

(17)

BLS的特征节点增强算法如图4所示。

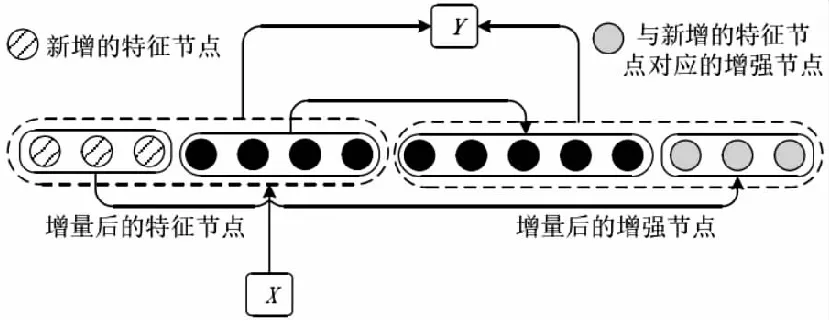
图4 BLS的特征节点增强算法

2.3 增加输入数据

在实际应用时,常常会有新数据的添加,宽度学习系统通过将新数据再次经过函数φ(XWe+βe)求得新的特征节点,并对新的特征节点经过非线性变换得到新的增强节点,构造了新的输入层,不需要重新训练整个模型,就能重建模型。

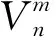
(18)

(19)

对应的伪逆矩阵为

(20)

(21)

因此,需要更新的权重结果为

(22)

其中,Ya是新增数据Xa所对应的标签值。

BLS的输入数据增加算法如图5所示。

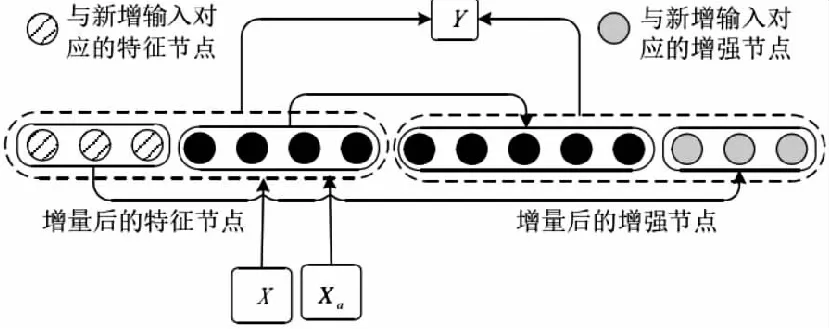
图5 BLS的输入数据增加算法

3 实验结果与分析

3.1 网络输入节点数量的选择

在宽度学习算法中,特征节点和增强节点的数量影响着模型的预测性能和运算速度,为了设置合适的参数值,本文基于包含三类地面目标的微多普勒数据集进行实验,分别为履带式装甲车、轮式装甲车和轮式民用车辆。其中履带式装甲车有2352帧数据,轮式民用车辆有5143帧数据,轮式装甲车有4095帧数据,每帧数据都有512个数据点。本文使用单帧作为样本,将数据集中80%作为训练集,20%作为测试集进行三类地面目标的分类实验。使用稀疏正则化约束,增强节点的缩放尺度设为0.8,迭代轮数为5。实验结果如表1所示。

表1 增加特征节点数量的分类结果(平均正确率,%)

本文又对增加增强节点数量进行了实验,如表2所示。

表2 增加增强节点数量的分类结果(平均正确率,%)

可以看到,当增强节点数量维持不变时,增加特征节点数量,分类正确率从91.03%逐渐增长至93.69%,以此时的特征节点为基数,增加增强节点数量,可以看到分类正确率有一个缓慢上升。随着每次增加特征节点和增强节点的数量,分类精度逐渐提高,但是当其达到一定数量时,再增加节点数量,正确率开始下降,这可能是过拟合造成的。故本文选择特征节点为40,增强节点数为8000作为后续实验的网络输入节点数量。

3.2 分类识别实验与分析

为验证宽度学习相比深度学习在微多普勒目标分类的优越性,本文搭建了一个双向长短记忆神经网络(Bi_LSTM)与宽度学习算法进行实验对比,使用的数据集有3种,除上一小节中介绍的针对三类地面目标的分类外,第二种是针对桨状飞机、喷气式飞机和直升机三类飞机的分类问题,其中桨状飞机有4588帧数据,喷气式飞机有1136帧数据,直升机有5336帧数据。第三种是针对单人和小分队的两类地面目标的分类问题,单人数据有4279帧数据,小分队数据有8704帧数据。由于数据样本不均衡,对上述三种数据均采取了数据增广手段,最后得到第二种分类中桨状飞机有4588帧数据,喷气式飞机有4544帧数据,直升机有5336帧数据;第三种分类中单人数据有8558帧数据,小分队数据有8704帧数据。选取70%作为训练集,10%作为验证集,20%作为测试集。在训练过程中,使用训练集进行训练,只使用验证集测试网络效果,以免数据泄露导致分类精度增高。本文实验所使用的编程语言为Matlab,采用单GPU运行。

双向长短记忆网络是一种应用十分广泛的深度神经网络,本文搭建的Bi_LSTM网络中有2个bilstm层、1个dropout层和1个全连接层,bilstm层中分别有128和64个隐藏单元。迭代轮数为20轮,小批量尺寸为16个样本,初始学习率设为0.001,并采用学习率衰减策略,每5轮衰减一次,每次衰减系数为0.5,并采用梯度截断策略将梯度范围限制为[-1,1],避免梯度爆炸问题,每轮迭代都打乱训练集数据。经过100轮迭代后,训练结束,图6为单人、小分队目标训练阶段,目标损失函数和准确率随着训练次数增加的变化曲线。图7、图8和图9分别表示本方法在三类数据上的混淆矩阵。

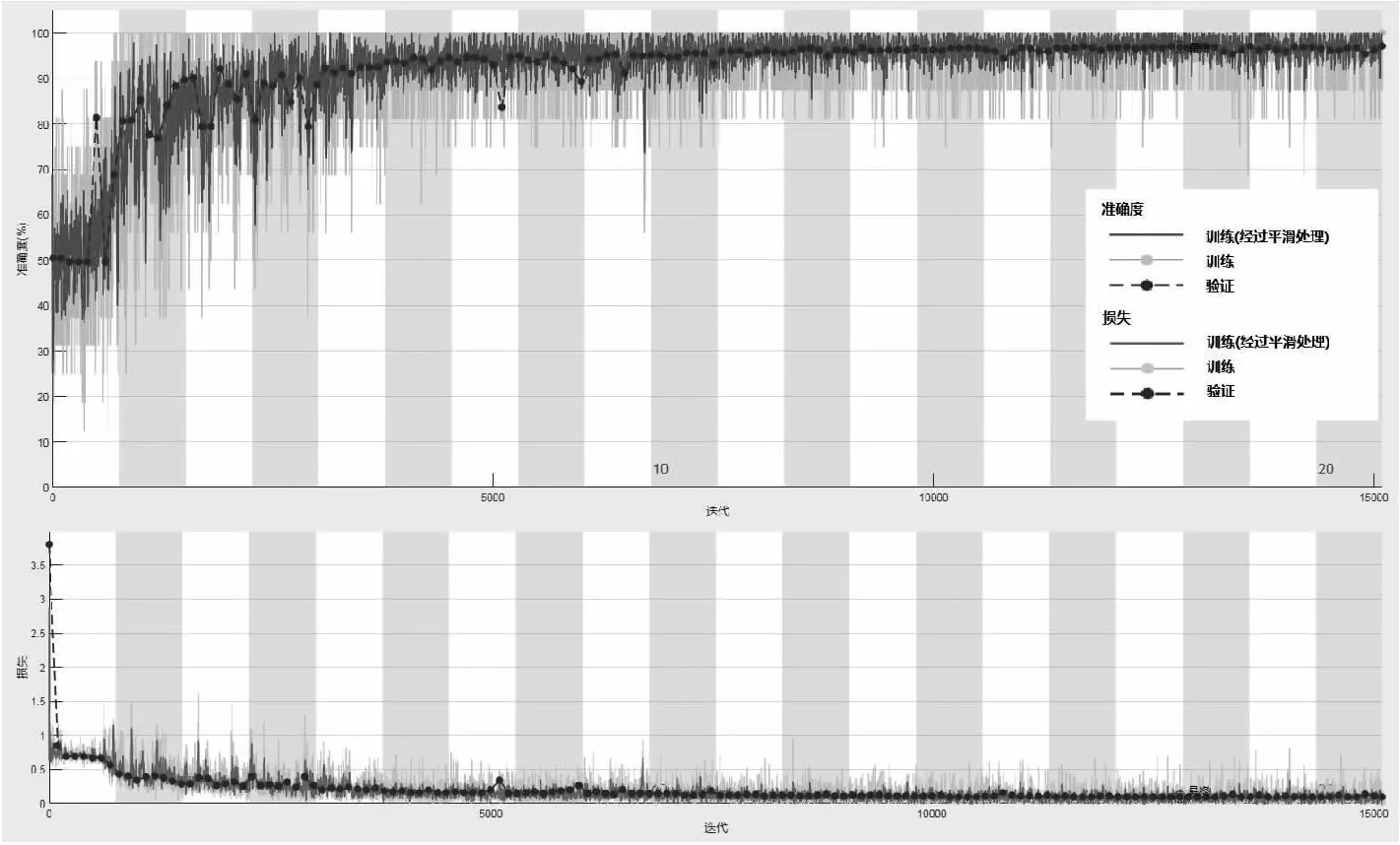
图6 单人、小分队目标损失函数和准确率随着训练次数增加的变化曲线

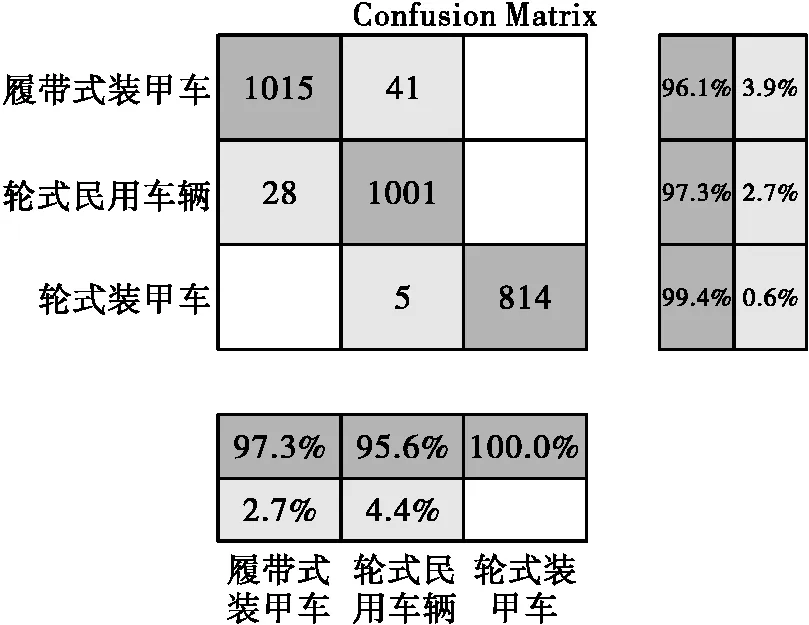
图7 Bi_LSTM在三类车辆数据上的混淆矩阵

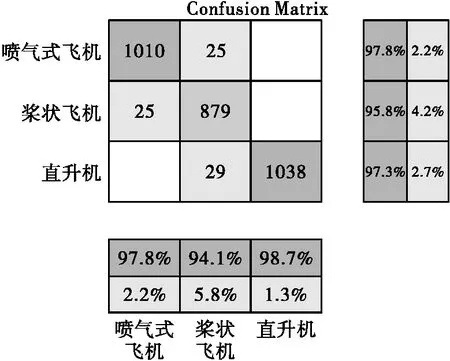
图8 Bi_LSTM在三类飞机数据上的混淆矩阵

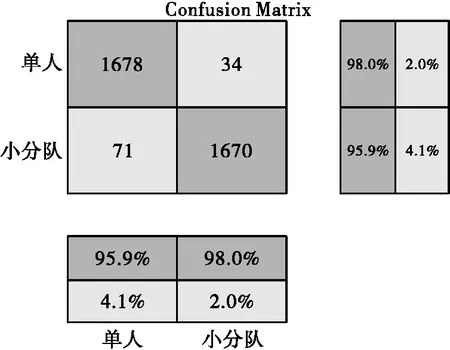
图9 Bi_LSTM在两类单人、小分队数据上的混淆矩阵

宽度学习算法中窗口数batchsize为10,迭代轮数为5轮。特征节点数和增强节点数分别设置为40和8000,稀疏正则化约束参数设为2～30,增强节点的缩放尺度设为0.8,激活函数都是采用tanh函数。迭代5轮求其平均值。图10、图11和图12分别表示本方法在三类数据上的混淆矩阵。

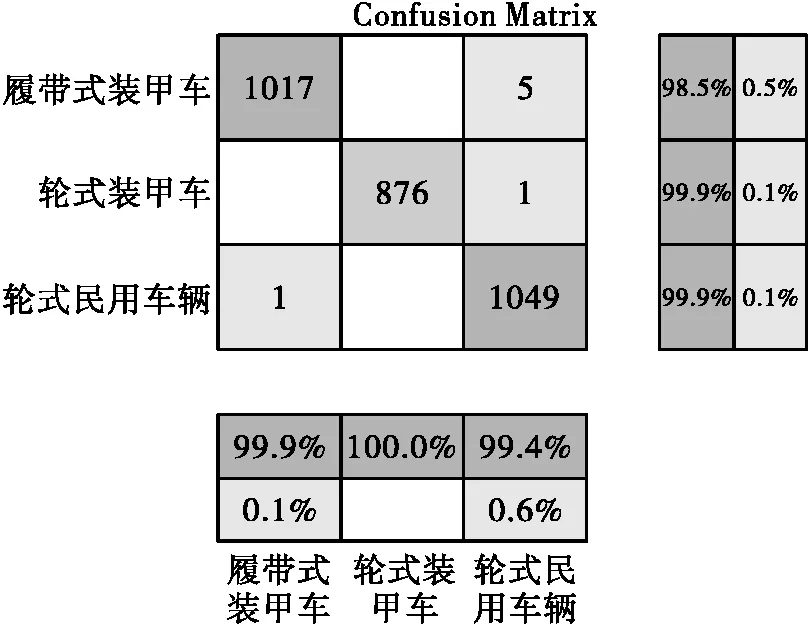
图10 宽度学习在三类车辆数据上的混淆矩阵

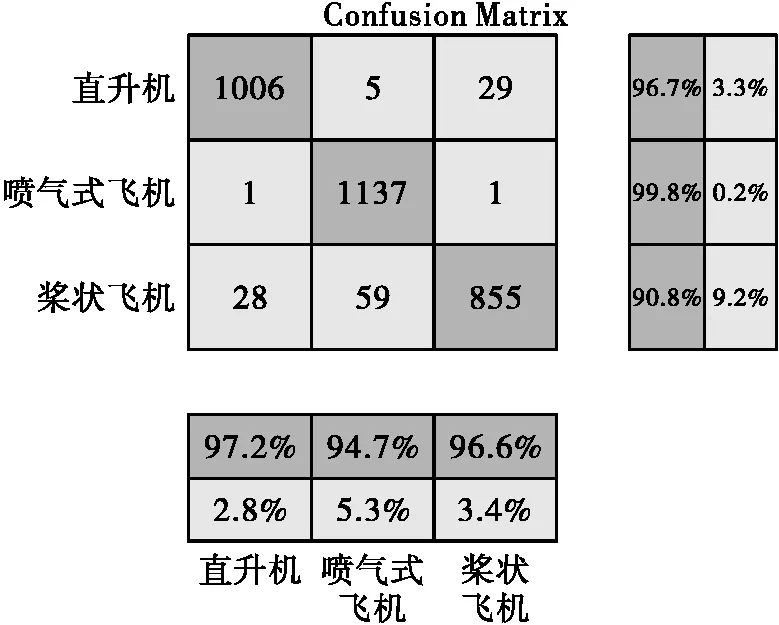
图11 宽度学习在三类飞机数据上的混淆矩阵

图12 宽度学习在两类单人、小分队数据上的混淆矩阵

为更明显地看出各个数据集的正确率,本文列出了所有结果如表3所示。其中,有效值保留到小数点后两位,而均值反映了两种算法在所有数据集上的分类效果的总体表现,可以看到Bi_LSTM算法和宽度学习算法的平均分类结果接近。

表3 两个算法在三种数据集上的分类结果(平均正确率,%)

接下来本文对比两个算法上在三种数据集上的训练时间,如图6所示为单人、小分队基于Bi_LSTM的目标损失函数和准确率随着训练次数增加的变化曲线。可以看到迭代到第20轮时,正确率趋于稳定,而本次用时共94′40″。其他数据集基于Bi_LSTM分类的训练时间也是此操作。如表4所示,可以看到Bi_LSTM的训练时间要明显慢于宽度学习。

表4 两个算法在三种数据集上的训练时间

综上所述,我们可以得出,在精度方面,宽度学习算法与Bi_LSTM深度学习算法在三类数据集分类实验中相差不多;而在训练速度方面,宽度学习算法远远快于Bi_LSTM算法。从这里体现出宽度学习算法应用于雷达的目标分类识别是可行的。

4 结束语

本文研究了宽度学习算法在窄带雷达目标识别方面的应用。首先介绍了宽度学习系统的基本概念以及BLS的增量学习算法,然后对BLS的网络输入节点数量进行了分析实验,接下来搭建了Bi_LSTM深度学习算法,在3种数据集上和宽度学习进行对比实验,得出宽度学习和Bi_LSTM算法在三种数据集上的平均分类正确率接近;也比较了两种算法的训练时间,证明了宽度学习的训练速度要远远快于深度学习,为窄带雷达微多普勒目标分类识别方面的问题提出了一种解决方法。