拱坝水平拱圈的动力稳定条件研究
孙敦本 任青文
(1.南京林业大学 土木工程学院, 南京 210037;2.河海大学 力学与材料学院, 南京 211100)
拱坝由于性能优良和工程造价相对较低,成为优选的坝型之一.拱坝在形状上呈凸向上游的挡水面,在库水压力作用下主要承受压应力,拉应力较小,使混凝土材料的强度得到充分发挥.随着混凝土强度等级的提高及优化设计技术的发展,拱坝的设计厚度有相对越来越薄的趋势.有些建成的薄高拱坝虽然满足坝体强度及拱座稳定的设计要求,但在使用过程中仍然会发生坝体严重开裂甚至毁坝的现象,如奥地利的Kohlbrein拱坝.通过对一些典型拱坝严重事故成因的剖析,一些学者从结构的稳定性方面探讨拱坝的破坏特征,认为坝体过薄的拱坝可能存在稳定问题,由于不满足稳定条件而导致坝体严重开裂,最终酿成严重事故.黄文熙[1]首先提出了拱坝的屈曲稳定问题,将薄壁拱坝简化为由水平拱段和竖向悬臂梁组成的网格结构,导出了静荷载作用下两个方向的临界荷载.杨树高等[2]基于拱梁分载法,用有限元软件分析了拱坝的拱圈和悬臂梁在静载作用下的稳定性问题,得出了拱坝坝顶拱圈最易失稳的结论.王正中等[3]基于圆弧拱圈的大曲率稳定理论来分析拱坝的稳定性,导出了临界荷载的计算公式,对Kohlbrein拱坝失事的主要原因进行了分析,认为该拱坝失事的主要原因并非强度问题,而是该坝体设计过薄,整体刚度太小导致坝体发生屈曲失稳破坏.任青文等[4]将水平拱圈假定为受匀布水压力的弹性圆拱,研究了拱坝强度破坏与失稳破坏的条件,在特定的条件下,坝体的破坏是由失稳引起的.这些研究都是从静力的角度对薄拱坝进行稳定性分析的,而实际上在地震作用下对拱坝的动力稳定分析更为必要.
由拱、梁分载法可知,在高拱坝的中上部,梁的作用变弱,主要是水平拱圈起控制作用.抛物线变曲率拱能够较好地解决坝体应力和拱座稳定这对矛盾,因而在工程中较常采用.按照我国混凝土拱坝设计规范(SL282—2018)对拱坝布置的要求,目前设计的有部分拱坝,拱圈的矢跨比小于1/5,从而可简化为扁拱(浅拱).Pi等[5-6]在分析扁拱坝的承载力时发现,由于扁拱存在非线性现象,实际承载能力要小于经典理论得到的结果,即按经典方法高估了扁拱的实际承载能力.黄朝煊[7]应用浅拱的非线性屈曲理论,通过定量简化计算分析,得出了拱坝柔度系数上限值与坝高之间的非线性函数关系式.
以上学者的研究多是从静力的角度研究拱坝稳定的临界荷载,没有研究动荷载下拱坝的稳定条件及位移随着频率变化的突变特性.本文在研究扁拱非线性振动的基础上[8],研究扁拱型拱坝水平拱圈动力稳定的条件及对应的物理、几何参数与地震系数之间的关系,进一步分析了拱坝不发生动力失稳破坏的“动力稳定裕度”,这也是保证大坝安全的必要条件.
1 非线性动力方程的建立
抛物线型双曲拱坝是一种实际工程中常被采用的坝型.随着设计施工水平的提高,从安全性和经济性的角度出发,在拱坝的体型上已趋向扁平化[9].设水平拱圈的初始拱轴线为理想抛物线,坐标方程为y0(x)=4hx(l-x)/l2,如图1所示.假定抛物线型扁拱截面的抗弯刚度EI和横截面积A为常量,材料的密度为ρ,扁拱的跨度为l,矢高为h.

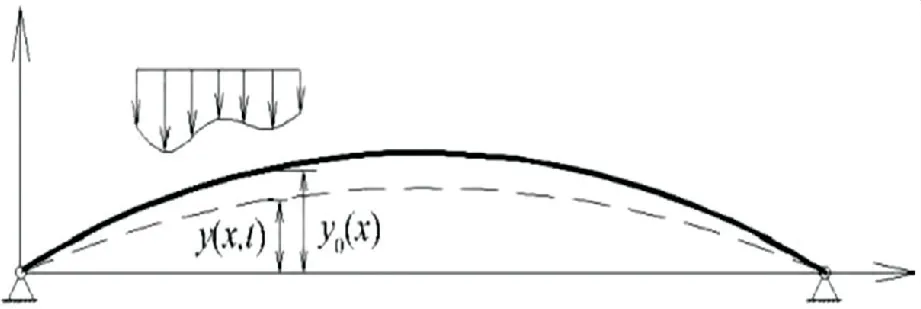
图1 双铰扁拱计算模型
设
式中:U0为地面加速度的幅值;k为地震系数;g为重力加速度.式(6)成为
2 拱圈振动的突变特性及稳定条件
抛物线型扁拱的振动方程(8)中,Y(t)为拱轴变形后的坐标;对于拱坝来说ω20通常小于零,为表示方便仍记为ω20;常数项Rk仅影响拱轴坐标的量值,不影响拱轴非线性变化的规律,分析时可略去.
设
可将式(8)化为振幅为D的双尖点突变模型,其平衡曲面(如图2所示)的标准形式为z3+az+b=0.
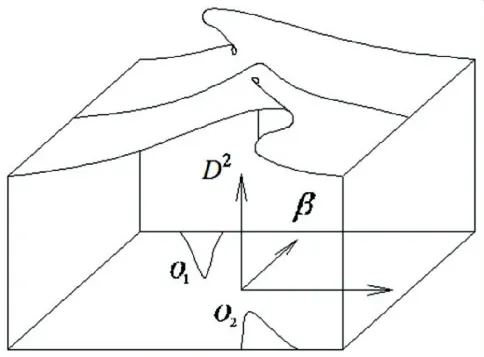
图2 双尖的突变模型
两个尖点坐标为o1(α1,β1),o2(α2,β2),其中
当β的取值范围在o1与o2的中间部分,即满足-32α32/81f2<β<-32α31/81f2时,振动系统具有很微弱的非线性特征,可视为线性稳定振动,位移不会发生突跳.由式(7)可知β>0,且当β>-32α31/81f2时,随着地震频率参数α的变化,系统共振发生畸变,拱圈振动位移会发生突跳.由于地震波的频率是随机的,所以当β>-32α31/81f2时,在地震作用下水平拱圈可能会发生非线性振动而破坏.
下面以一薄高拱坝为例进行动力稳定性分析.拱坝位于深凹的“V”型峡谷中,当地的设防地震加速度为0.557g,最大坝高200 m.现取坝顶拱圈进行分析.该拱圈水平跨度180 m,厚度2 m,拱矢高12 m,该坝水平拱圈呈扁平拱.对该水平拱圈进行动力分析时,考虑动水压力的影响,将动水压力等效为附加在坝面上一定质量水体的惯性力[10]:
式中:H为坝前水深;ρ为水体的密度;h为待分析坝面处的水深.计算时取库水为满库,取坝顶1 m 高的拱圈进行计算,坝体材料的弹性模量E=2.0×1010N/m2,阻尼比按规范要求取0.03~0.05,本文取0.03.由计算可知β=0.570,β1=0.568,β>β1,根据抛物线型扁拱的稳定条件,拱圈不符合系统稳定的条件,振动时位移存在突变现象.
图3为拱圈振动幅值与频率参数α之间的关系,当频率参数α从大到小变化时,拱轴坐标振动幅值逐渐增加,但并不是在自振频率处发生共振,而是在偏离自振频率一定范围处振幅最大,之后振幅突然跳到较小值;当频率参数α从小到大变化时,振动幅值也会发生突跳现象.在激励频率的变化过程中振幅的这种突跳会对拱圈造成很大的冲击,使拱圈的体形发生突变,导致拱圈破坏.地震过程中地震波的频率范围很广,在拱圈发生非线性振动时,很容易造成拱圈失稳破坏.可见,薄高拱坝既然存在着动力非线性振动现象,因此在设计拱坝时就应避免这种现象的出现,通过选取合理的几何、物理参数使拱坝处于稳定振动状态.
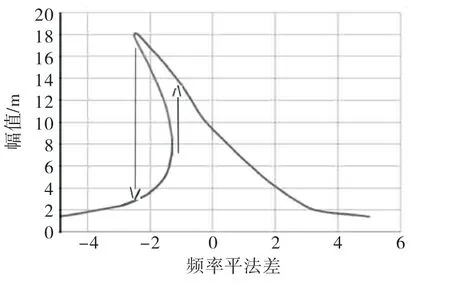
图3 位移幅值-频率的平法差α
设η=ξω0,当β>0,所以β对应的稳定区域为β∈(0,β1),扁拱的稳定条件为
式中:Rξ=(-6ξ2+2ξ9ξ2+3)3.式(14)是薄高拱坝顶部的水平拱圈不发生动力失稳破坏的必要条件.当式(14)不满足动力稳定的条件时,地震波频率参数α很容易穿过分叉集从而造成大坝拱圈的失稳破坏,因此,失稳条件可以作为水平拱圈的地震破坏准则.
3 拱圈动力稳定裕度分析
理论上,公式(14)右边与左边之比<1时,表明水平拱圈在某些地震频率成分下会发生动力失稳;反之,水平拱圈是动力稳定的,且右边与左边之比越大越不容易发生动力失稳.实际工程中,由于混凝土是脆性材料,在振动过程中混凝土容易开裂,造成水平拱圈的刚度降低,当公式(14)右边与左边之比>1也可能发生动力失稳,这个比值的限值肯定要比1大,那么比值要为多少才不会发生动力失稳呢? 本文把这个最小的比值定义为“动力稳定裕度”.这需要通过实验或实际震害调查才能确定.混凝土拱坝遭受震害的实例较少,还未有直接因地震作用而溃坝的实例[11].
本文通过上述的分析结果与其他学者的模型试验或数值分析结果的对比来确定稳定裕度.大岗山拱坝高210 m,设计水平地震加速度为0.557g,是目前设防烈度最高的拱坝.钟红等[12]进行了几何比尺为273的动力模型试验和数值模拟,所得的破坏形态两者基本一致,均在顶拱中部附近出现破坏.周晶等[13]对黄河上的一座双曲拱坝进行了动力模型试验研究,该坝最大坝高165 m,顶拱弧长422 m,坝底最大厚度45 m,坝顶厚度8.0 m.试验结果表明坝顶中部是坝体抗震的薄弱部位.当加速度为0.8g时,坝顶中部出现纵横宏观裂缝,局部发生破坏.王海波等[14]对小湾拱坝进行了1∶300的振动台模型试验,小湾拱坝最大坝高294.5 m,坝顶拱冠梁厚度12 m,拱顶上游弦长798.5 m,宽高比2.73,厚高比0.25.试验中考虑了坝体与库水、山体与坝体的动力相互作用,所得结果也是坝顶中部率先发生破坏.可见拱坝顶部的拱圈是抗震的薄弱部位.
针对以上3个试验,本文根据前述的理论分析,选取大坝顶部的拱圈,使用实际工程中的物理几何参数对其进行动力稳定分析,所得结果见表1.
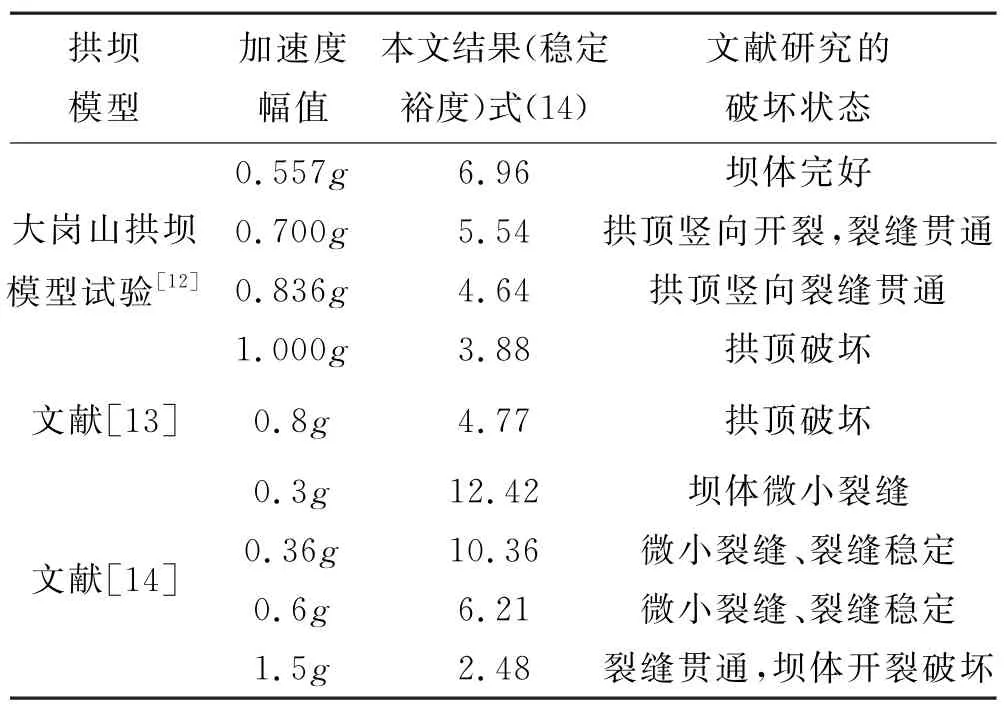
表1 动力稳定裕度计算表
由表1可知,对拱坝模型进行振动台试验破坏时对应的最小稳定裕度按式(14)计算不应小于5.54,这是通过3组试验结果对比得到的比较安全的稳定裕度限值,小于这个限值可能发生非线性动力失稳.
进一步根据搜集到的资料,对一些典型的拱坝进行了动力稳定裕度分析,并与相关学者的数值模拟结果进行了对比,结果见表2.
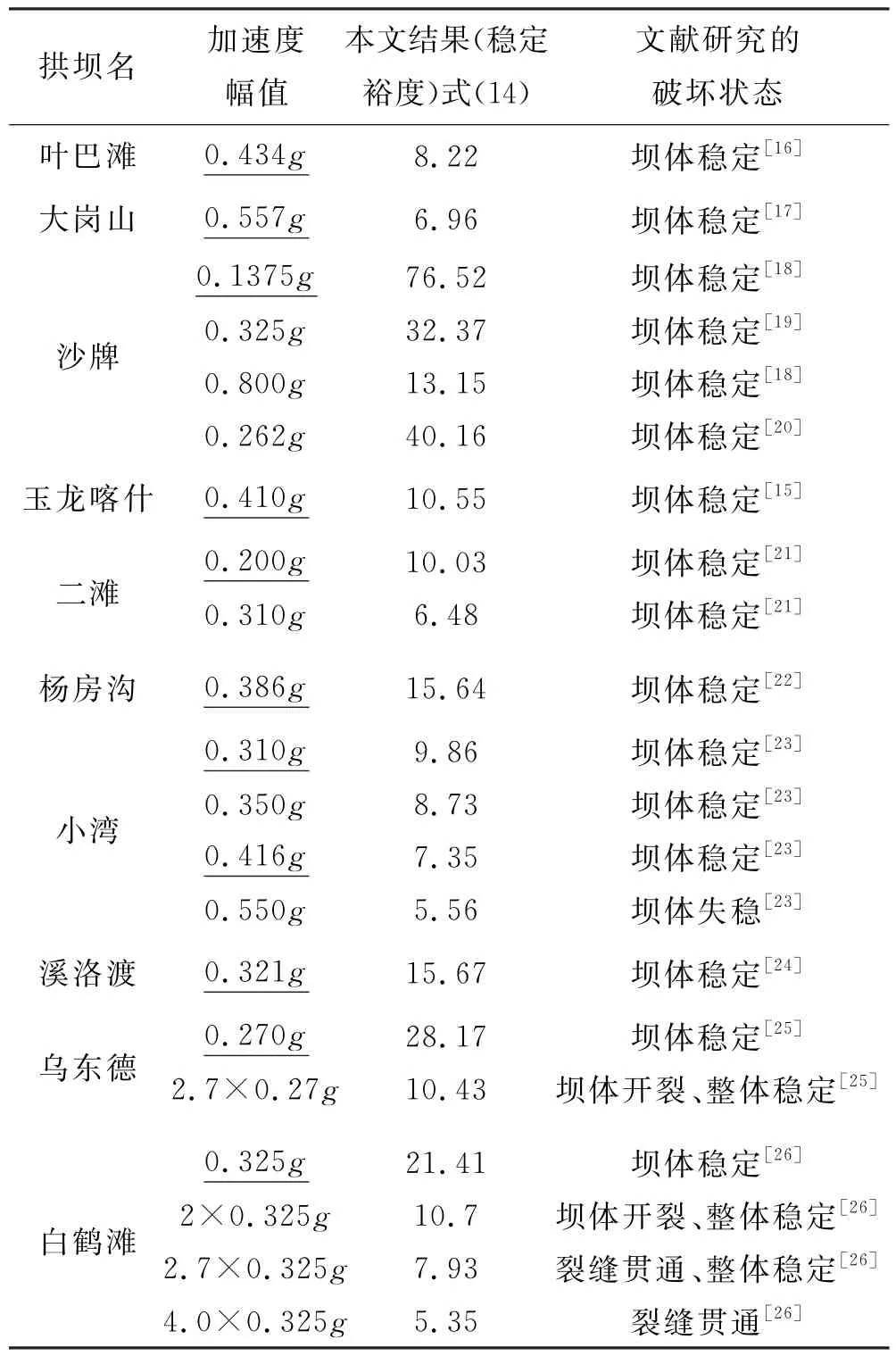
表2 一些典型拱坝稳定裕度计算表
表2中加速度幅值加下划线(用“”表示)者为设计加速度.从该表可以看出我国设计的拱坝均大于前述的动力稳定裕度限值5.54,表明在我国规范规定的地震设防加速度下,这些拱坝不可能发生地震作用下的动力失稳破坏.以沙牌拱坝为例,坝址的基本设防烈度为7度,拱坝以100年基准期、超越概率2%确定设计概率水准,相应的水平地震加速度峰值为0.137 5g.以此进行拱坝设计,对应本文的动力稳定裕度为76.52,远高于最小稳定裕度5.54的限值要求.汶川地震时沙牌坝址的水平向地震加速度峰值0.262g,对应的动力稳定裕度为40.16,该坝经受了此次大地震的考验[20].王仁坤等[20]分析了沙牌拱坝在水平向地震加速度峰值为0.8g时也是安全的,该峰值加速度对应的动力稳定裕度为13.15,也处于动力稳定状态,不会发生动力失稳.涂劲等[23]分析了小湾拱坝的抗震性能,在1.3倍最大可信地震作用下,即对应的峰值加速度为0.55g时该坝破坏.本文分析的结果是,在该峰值加速度下,由式(14)计算得到小湾拱坝对应的动力稳定裕度为5.56,略高于最小稳定裕度5.54的限值要求,处于发生动力失稳的边缘、接近破坏.二滩拱坝在地震加速度为0.31g时,采用式(14)判别的稳定裕度为6.48,高于5.54的限值,坝体动力稳定,与文献[21]的结论一致.白鹤滩拱坝在地震超载系数为4.0时,文献[26]只给出裂缝贯通的结论,按照本文的分析已经失稳破坏.
4 结 论
本文根据突变理论,导出抛物线形拱坝水平拱圈的地震破坏准则.在对比他人振动模型实验和数值研究的基础上,提出了“动力稳定裕度”的概念,给出拱坝水平拱圈动力稳定裕度的最小限值为5.54.该限值与其他学者对一些拱坝的抗震评估结果吻合较好.本文提出的动力稳定裕度的限值可为拱坝的初步设计及地震评估提供有益的参考.

