基于绿证机制与条件风险价值的风光水网联合优化调度策略

李咸善 杨 拯

(1.三峡大学 电气与新能源学院, 湖北 宜昌 443002;2.深圳供电局有限公司, 广东 深圳 518048)

在以风光新能源为主体的新型电力系统建设中,由于风光新能源的随机波动性、不可控性和不确定性,其高占比大规模入网后会给电网造成大频度冲击,难以跟踪负荷变化,造成电网调度难度大、调节资源配置成本高和调度方案执行风险大等新能源消纳瓶颈问题,在传统化石型调节资源占比受限的情况下,需另寻大规模的清洁型调节资源加以解决.规模庞大、技术成熟的水电是具有良好调节性能的高灵活性电源,是中国现在和未来一段时期新能源大规模消纳最现实、最可靠的选择[1-2].为此,本文以梯级水电为调节电源,将梯级水电和风光集团组成联盟,研究基于梯级水电调节的风光水联合出力对电网负荷跟踪的调度策略,解决梯级水电调节补偿策略、不确定性风险规避、多参与主体利益共赢交易机制、联盟效益合理分配机制等关键问题,促进大规模风光新能源消纳.

梯级水电参与大规模风光消纳的调节调度,势必损失其既定利益.为了激发水电参与大规模新能源调节消纳的积极性,本文采用调节补偿策略,由风光集团依据其调节量的大小支付梯级水电调节补偿费用,确保水电调节利益;考虑风光水不确定性风险成本,以减小调度方案的不确定性执行风险;实施基于主从博弈优化模型的风光水联盟与区域电网双边交易,最大化联盟效益和区域电网效益;通过非对称纳什议价优化水电调节补偿电价,实现多成员利益较合作前利益得到有效提升和联盟利益的公平合理分配,保证联盟稳定性的同时,激励梯级水电参与风光消纳.

在电力系统调度中,源荷不确定性影响的衡量方法通常有风险价值法VaR(Value at Risk)和条件风险价值法CVaR(Conditional Value at Risk).VaR 表示在一定置信水平下的最大收益损失值,CVaR 表示收益损失高于VaR 的所有损失期望值,CVaR 可在原有截尾数溢出时进行补充,因此CVaR 在风险度量与风险管理中得到了较为广泛的运用[3].文献[4]利用CVaR 理论衡量虚拟电厂中风光不确定性影响,在风险可控范围内最大化虚拟电厂的收益;文献[5]利用CVaR 作为度量负荷与负荷需求误差的指标,考虑风险成本使得省内市场运行成本最小;文献[6]用CVaR表示由于灵活性不足给电力系统带来的风险损失,考虑风险成本与运行成本最小制定优化调度策略.

在梯级水电与新能源联合优化调度方面,目前的研究主要集中于风光水资源的互补性调度,鲜有涉及基于水电调节的风光水网联合优化调度的研究.文献[7]通过考虑水风互补,构建了水火风互补优化调度模型,最大化整体效益;文献[8]利用梯级水电储能大、调节能力强的特点,建立含风、光、水多能互补的发电端,使发电端出力曲线具有光滑与削峰填谷的效果;文献[9]在构建风光水互补指标框架下,证明了风光水在日内对负荷有良好的跟踪作用,在日内时间尺度具有良好的互补性.

风光水结盟联合优化调度运行时,涉及不同的利益主体,需要公平合理的联盟利润分配方案,保证各参与主体较未合作前能有利益的提升,才能保持合作联盟的稳定性.文献[10]利用能量映射函数量化各主体贡献大小,在保证利润提升的情况下利用非对称纳什谈判尽可能地保证利润分配的公平性;文献[11]利用共享容量作为产销者与储能运营商的议价能力,利用能量映射量化其议价能力,进行联盟成员利润分配.

为了促进电网侧改变能源结构的意愿,降低非可再生能源比例,在电网侧实施可再生能源配额制(renewable portfolio standard,RPS)与绿证交易机制(tradable green certificate,TGC)对电网进行考核[12],是一种有效的政策措施.文献[13]利用绿色证书交易对区域综合系统进行考核,得出该方法可有效提高绿电比例和经济性,能有效体现新能源环保价值;文献[14]同时考虑了碳配额与绿证交易,碳配额与绿证交易同时进行优化能较好地实现碳减排目标.

博弈理论能准确表示多主体之间的相互竞争关系,主从博弈在能源系统优化调度中得到了广泛应用.文献[15]利用能源枢纽运营商和用户之间的主从博弈,兼顾双方利益,实现能源枢纽经济低碳运行.文献[16]构建了微网运营商和用户聚合商之间的主从博弈模型,权衡两者之间利益,实现双方利益的共赢.

基于以上综述,本文提出了基于绿证机制与条件风险价值的风光水联合优化调度的三阶段优化调度策略.第一阶段,考虑风光水条件风险价值,构建电网运营商与风光水合作联盟的主从博弈模型,电网运营商在满足RPS情况下以利益最大化为目标制定购电电价,风光水合作联盟以收益最大化制定售电策略,通过风光水合作联盟进行负荷跟踪与未进行负荷跟踪时的功率对比确定梯级水电的调整功率,利用遗传算法嵌套Cplex 求解器求解主从博弈模型;第二阶段,风光水合作联盟利益分配,构建非对称纳什议价模型,通过第一阶段求解的梯级水电对各风光集团的调整功率作为各风光集团的议价能力,优化制定内部补偿电价,进行联盟效益的公平合理分配,保证合作联盟的稳定,该阶段模型用ADMM 算法进行求解;第三阶段,梯级水电调整功率分配通过以电定水,将第一阶段为实现风光水联合出力跟踪负荷的梯级水电调整功率分配至各个梯级水电站,该阶段模型利用遗传算法进行求解.最后,通过仿真算例对本文方法的有效性进行验证分析.

1 风光不确定性场景模拟与条件风险评估

为考虑风光水联盟中的风光不确定性给区域电网运营带来的经济影响,首先建立风光不确定性场景模型及不确定性条件风险价值评估模型作为研究的基础.

1.1 风光预测误差的不确定性表达

风光不确定性是指风光预测误差的随机性.风光预测误差表示风光实际功率与其预测功率的差值,一般呈现正态分布[17],见式(1)～(4).

式中:F(·)表示概率分布函数;ΔPWt、ΔPSt分别为风电、光电实际出力与预测出力的差值;PRWt、PRSt分别为风电、光电的实际出力,PPWt、PPSt分别为风电、光电的预测出力,σWt、σSt分别为t时刻风电、光电实际出力与预测出力误差的标准差.

根据概率论,两个服从正态分布的随机变量,其联合也服从正态分布.

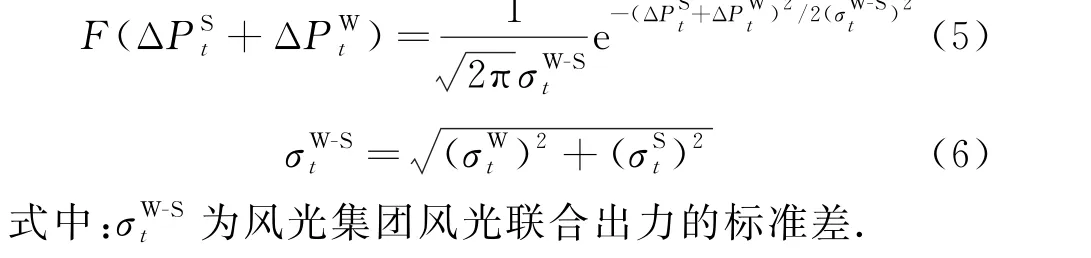
1.2 风光随机性场景生成与削减

采用随机抽样方法模拟风光出力随机波动性场景.拉丁超立方抽样是一种从多元参数分布中近似随机抽样的方法[18],属于分层抽样技术,相比蒙特卡罗抽样法,能够以较小的采样次数获得较高的采样精度,其具有覆盖空间广的特点.本文采用拉丁超立方抽样生成初始500个场景.

式中:K为削减的场景集合.

1.3 风光随机性场景生成与削减

在区域电网与风光水合作联盟的主从博弈模型中,风光水合作联盟的实际出力与预测出力存在误差.若某时段实际出力大于预测出力,误差为正,则区域电网需面临承担更多的购电成本风险,使得区域电网的可获得利益理论上减少;若实际出力小于预测出力,误差为负,区域电网则需要用更多的购电成本来购买本区域内的其他能源,同时面临着因消纳新能源不足带来的购买绿证的费用风险.

本文采用条件风险价值CVaR[5]法来衡量由于风光预测误差不确定性导致的区域电网可能面临的条件风险成本CVaR.若此时置信度为β,将成本概率分布为(1-β)对应的值作为区域电网运行成本的VaR 值,所以使得区域电网的运行成本大于VaR 值的概率小于(1-β),则此时区域电网的CVaR 如式(9)所示.

式中:C为区域电网的实际运行成本;ηi为辅助变量;ζ为区域电网运行的VaR 值.上述两式,可以对超过区域电网运行商运行成本VaR 值的场景进行优化,降低总体的运行成本.

2 区域电网与风光水联盟联合运行框架

图1为区域电网与风光水联盟联合优化调度框架图.区域电网含自有火力发电厂和少量风光发电厂,从风光水联盟购买新能源,满足本区域负荷要求及RPS考核要求,同时降低火电比例,RPS考核缺量再从绿证市场购买绿证补充.

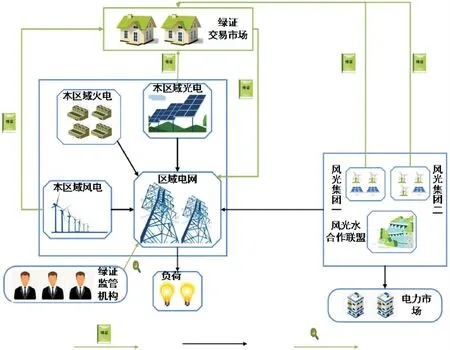
图1 区域电网与风光水联盟联合调度框架

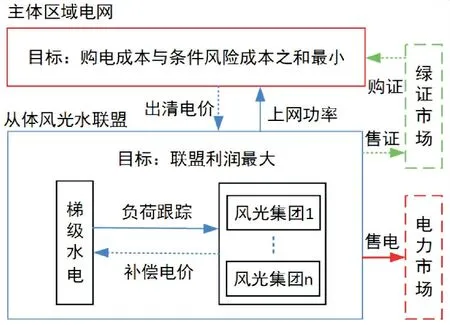
图2 主从博弈模型结构图

为了减小大规模新能源接入给电网带来的巨大冲击及调度压力,区域电网要求风光新能源进行负荷跟踪调度.为此,风光新能源与梯级水电组成风光水合作联盟,通过梯级水电的调节实现风光水联合出力对电网净负荷(本区域负荷减去本区域新能源出力)的跟踪,风光集团给予梯级水电调节补偿费用以维持联盟的稳定性.

3 区域电网与风光水联盟联合运行优化调度模型

按照能量调度决策及模型求解顺序,分3个阶段建立风光水联盟与区域电网联合运行的优化调度模型.第一阶段:在考虑条件风险成本的情况下建立区域电网与风光水合作联盟的主从博弈模型,同时将梯级水电在进行负荷跟踪前与未进行负荷跟踪时的功率进行对比,可求出梯级水电对各风光集团的调节功率;第二阶段:根据梯级水电对各风光集团的调节功率,可得出每个风光集团的议价能力,建立风光水的非对称纳什议价模型,进行合作联盟的利润分配;第三阶段,建立梯级水电的负荷跟踪调节功率在梯级水电内部的优化分配模型.

3.1 区域电网与风光水合作联盟的主从博弈模型

区域电网与风光水合作联盟的双边交易,通过主从博弈优化调度模型来实现.上层区域电网考虑风光不确定性与负荷不确定性带来的条件风险成本,发布购电电价购买风光水联盟出力,满足RPS考核,希望风光水联合出力跟踪负荷变化以减小对电网的冲击,最后火电进行补充,实现电网功率平衡,达到区域电网运行成本与风险成本最小;下层风光水合作联盟根据区域电网制定的购电电价来决定自己的售电量,达到所获利润最大化.

3.1.1 上层博弈主体区域电网优化模型

3.1.1.1 梯级水电未进行负荷跟踪时区域电网目标函数

目标函数:区域电网运行成本与条件风险成本之和最小

式中:-为电网优先消纳自身新能源之后的净负荷.

③上层综合目标函数.采用梯形模糊法对目标函数C2和C3进行归一化处理[20],通过加权法得到综合目标函数,见式(16).

式中:e为权重系数;ψ(C2)和ψ(C3)为式(14)、(15)归一化的目标函数.

3.1.1.3 约束条件

①目标函数C1的功率平衡约束

对应于目标函数C1,未进行负荷跟踪时的电网功率平衡约束见式(17).

3.1.2 下层从体风光水联盟优化模型

风光水集团合作运行,以联盟效益最大为目标建立风光水联盟优化模型.作为比较,风光水联盟有两种合作模式:一种是不考虑梯级水电调节、联盟出力不跟踪电网负荷变化的合作模式;一种是本文采用的考虑梯级水电调节的联盟出力跟踪电网负荷变化的合作模式.通过两种模式的研究,一方面可以比较两种模式的调度效果,另一方面也可以得出梯级水电用于联盟出力跟踪负荷变化的调节量大小,以备第二阶段联盟效益分配之用.

同时也建立了风光集团不参与合作联盟的效益模型,以备第二阶段联盟效益分配之用.

3.1.2.1 风光水合作联盟目标函数

风光水联盟及其成员的电力交易分配关系见式(26).

3.1.2.2 风光水不合作时的目标函数

从式(31)、(32)可以看出,式(25)联盟总收益C5中的联盟内部补偿收益互相抵消了,经过主从博弈模型获得的联盟收益及各成员收益并不包含补偿收益,故称之为伪利润.考虑内部补偿利润的联盟各成员利润计算需要通过第二阶段的非对称纳什议价模型来解决,并需要建立各集团未参与合作联盟的独立运营效益模型,如下所示.

1)风光集团不参与合作联盟的效益模型

当风光集团独立参与电网交易时,未调节跟踪电网负荷变化的大规模风光接入电网,会给电网造成巨大冲击.为此,目标电网将会压低风光上网电价和电量.此时风光集团的综合效益GGi,t,0为其售电收益与风光维护成本之差.

式中:αi,0为第i个风光集团未调节风光出力的上网销售电价.

2)梯级水电集团不参与合作联盟的收益

梯级水电未与风光集团合作时的综合效益GHt,0为梯级水电上网利润与维护成本之差.

式中:Qmin,Qmax分别为场景w下第j级梯级水电t时刻允许流量的最小、最大值.

④梯级水电库容约束

式中:vmin,vmax分别为场景w下第j级梯级水电t时刻允许的库容最小、最大值.

⑤风光集团上网功率约束

⑥梯级水电进行负荷跟踪调整功率约束

式中:Δ为调整功率允许的最大值.

3.2 风光水合作联盟的利润分配与非对称纳什议价模型的构建

通过第一阶段的求解,可将联盟合作时可获得的利润求解出来.为了保持联盟的稳定,在梯级水电进行负荷跟踪时,风光集团需要对梯级水电进行补偿.而在第一阶段主从博弈计算过程中下层从体求解合作时的最大收益时,补偿利润在计算过程中消去了,无法在第一阶段进行求解.因此,需要进行第二阶段的非对称纳什议价环节,来计算风光集团与梯级水电实际所获得的收益.

3.2.1 基于非对称纳什议价模型的风光水联盟利润分配

当多个个体之间互动时,多个个体朝有利于自己发展或获利的方向进行决策,称为博弈.其中,合作博弈是指个体之间通过某种协议和机制,使得各个参与者不再显示强对抗的关系,通过合理的利润分配优化,使得各个个体能获得较合作以前更多的利润.

普通的纳什议价模型的解决方案只是最大化所有个体的利益乘积,这样计算通常会使得所有个体获得相同的利益提升,然而在实际情况中,这样是不合理的,因为不同个体由于信息不对称和参与情况不同,对合作贡献度也不一致,因此,贡献较大的应该有权获得更大的收益.本文中,由于梯级水电对各风光集团的调节功率不一致,因此对每个风光集团的贡献也不一致,梯级水电调节功率较大的风光集团理应承担更多的补偿费用,以此来体现利润分配的合理性.基于以上情况,提出了非对称纳什议价模型来进行利润分配.

用梯级水电对于各风光集团的调节功率,作为各风光集团的议价能力,见式(42).

3.3 梯级水电进行负荷跟踪调节功率的分配

第三阶段将进行“以电定水”,将第一阶段所求的将不进行负荷跟踪时的梯级水电出力与进行负荷跟踪时的梯级水电出力进行对比,可得出梯级水电进行负荷跟踪时的总调节功率,然后通过最小耗水量进行优化,将调节功率分至各梯级水电站.

①梯级水电各级水电站出力模型

②梯级水电耗水量最小目标函数

式中:W(t)为梯级水电调节功率总耗水量.

梯级电站“以电定水”的调度约束与(36)～(39)相同.

4 整体模型求解

总体三阶段模型的求解分别采用遗传算法嵌套cplex求解器、ADMM 和GA 算法进行求解.

4.1 第一阶段区域电网运行商与风光水合作联盟主从博弈求解

电网先根据自身情况与条件风险成本制定一天内的购电电价的策略集合,风光水合作联盟根据电网制定的电价与电力市场电价实时调整自己的上网功率.电网运营商和风光水合作联盟交互变量为购电电价和对应的上网功率.当电网运营商制定电价过低时,风光水合作联盟将动态调整售入电力市场与电网的功率;反之,电网运营商将根据风光水合作联盟的上网功率制定自己的购电电价,直至找到两者的最优解.电网运营商与风光水合作联盟利益冲突,且求解有先后顺序,因此为主从博弈问题,如式(47)所示.上网功率.求解步骤如下.

步骤1:初始化电网运营商和风光水联盟参数数据,设定迭代次数d=0,设定种群总数为100,迭代总数为50,变异率3%,交叉率75%;

步骤2:首先随机生成h组对应的电网购电电价,将购电电价传给下层的风光水合作联盟;

步骤3:d=d+1;

步骤8:若d＞50,结束程序,否则,返回步骤3.

4.2 第二阶段非对称纳什议价的求解

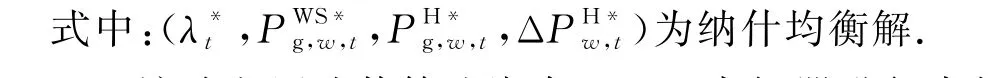
该阶段用遗传算法嵌套Cplex求解器进行求解.首先利用遗传算法初始化,更新上电网运营商的购电电价,下层问题用Cplex求解器求解风光水合作联盟

步骤5:判断是否达到误差精度或最大迭代次数,若不能满足收敛条件,则返回步骤2继续迭代;若满足收敛条件,则计算结束,输出结果.

4.3 第三阶段梯级水电以电定水求解

采用以电定水优化模型,将第一阶段的梯级水电跟踪负荷的调节功率ΔPHw,t分配到各级电站,达到耗水量最小,采用GA 算法求解.

已知调整功率与流量和水头关系如式(53)所示.

式中:F3如式(46)所示.

根据优化出的Qi(t)、Hi(t)可计算每一级水电对应时刻的调整出力.

4.4 总体模型求解流程

总体模型三阶段求解流程如图3所示.

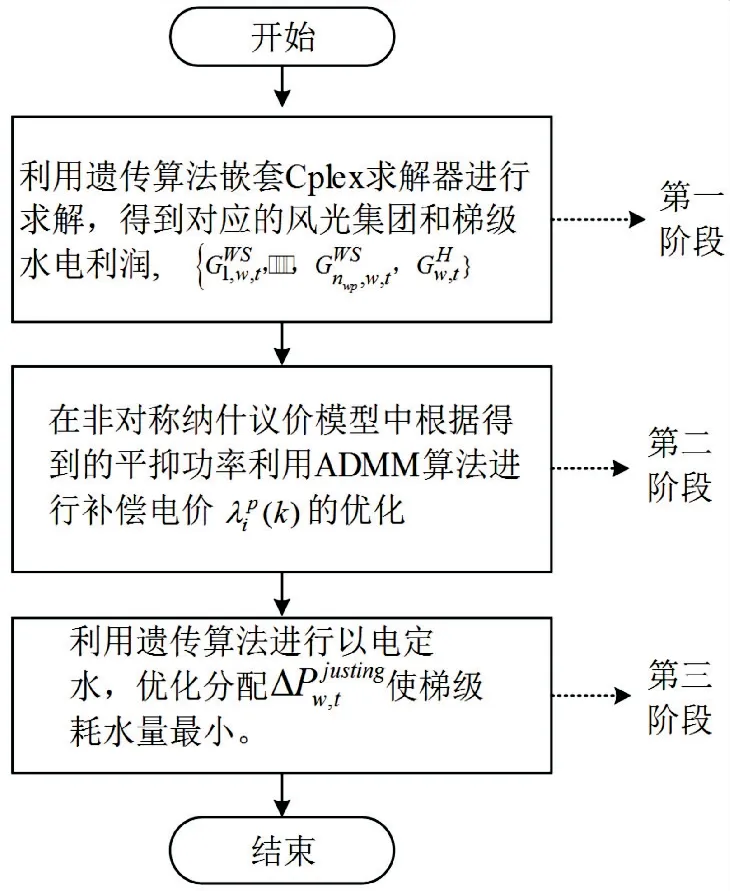
图3 三阶段求解流程图

首先在第一阶段,通过主从博弈模型求出梯级水电和风光集团的伪利润,传递给第二阶段;在第二阶段中,利用ADMM 算法对补偿电价进行优化计算,可得出对应的各主体的利润;第三阶段,利用遗传算法将第一阶段计算得到的调节功率优化分配至各个梯级水电站.

5 仿真算例分析

5.1 算例参数

算例场景设定为某区域电网自备火力发电和少量新能源发电,以及另一流域地区的两个大规模风光集团和两级梯级水电集团组成风光水合作联盟,区域电网从风光水合作联盟跨区域购电满足考核目标,其中,绿证购买价格为1 300元/(MW·h),区域电网本区域火电发电成本系数分别为0.26,140,2 330,惩罚价格1500元/MW,调度周期为24 h,每个时段为1 h.

5.2 仿真结果及分析

5.2.1 风光集团场景生成

由拉丁超立方抽样生成大量场景,然后再利用概率距离进行场景缩减,得到10个典型场景,如图4～5所示,场景概率见表1.

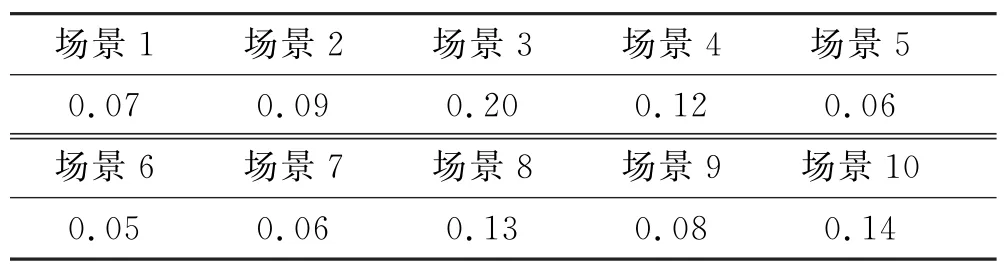
表1 风光集团各场景发生概率

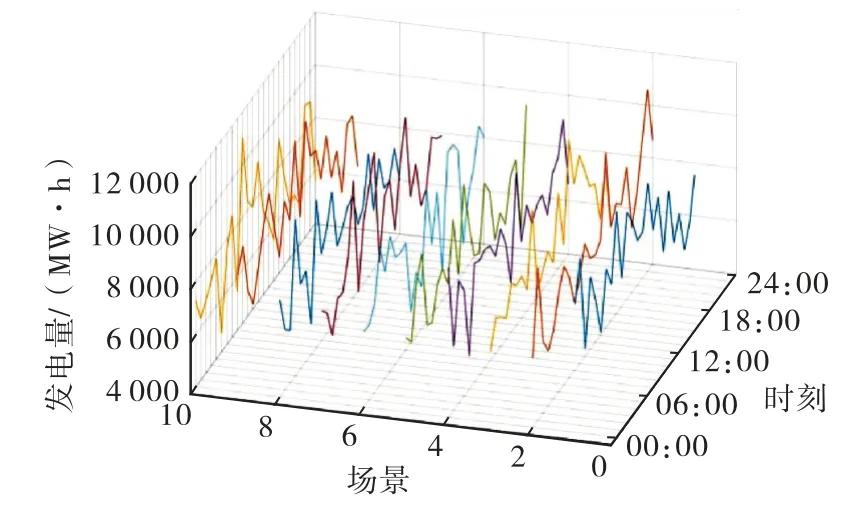
图4 风光集团1场景图

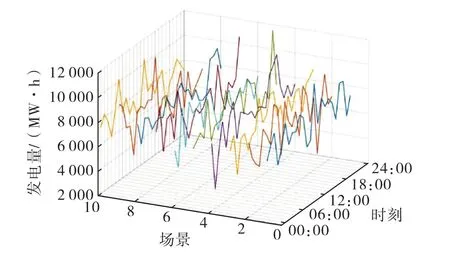
图5 风光集团2场景图

由表1可知,场景3发生的概率最大,因此本文主要展示场景3的结果分析.

5.2.2 区域电网与风光集团博弈分析

图6为区域电网没有与风光水联盟交易时,区域电网通过本区域能源满足负荷需求.

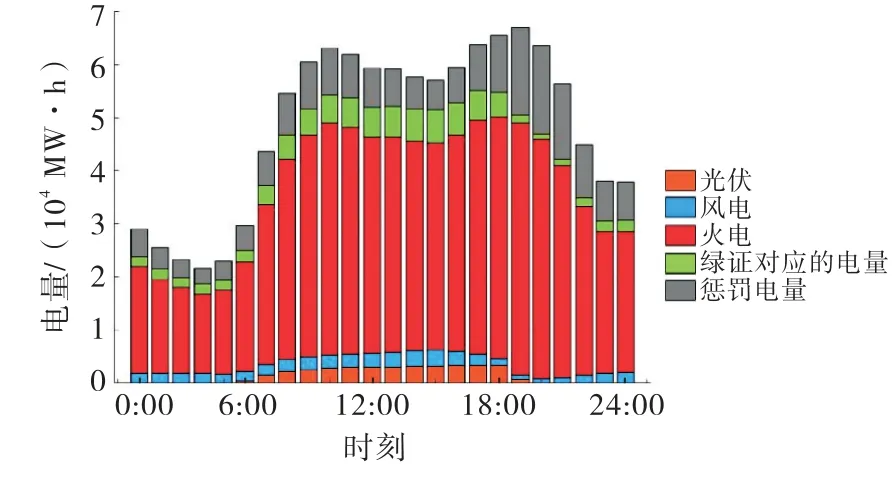
图6 区域电网未从风光水联盟购电时出力

由图6可以看出,此时的能源组成以火电为主,少量的本区域风光新能源为辅.由于本区域的新能源资源有限,区域电网不能满足RPS考核要求,需要从绿证市场购买大量绿证来满足需求,如若购买绿证仍然不满足RPS考核,则需要付出相应的惩罚费用,此时区域电网的相关运行成本则十分昂贵.

图7为区域电网与风光水联盟进行交易购买联盟电量.其中,联盟将上网风光功率进一步通过梯级水电调节,使联盟总上网出力跟踪了电网负荷变化,以减小对电网的冲击.此时电网消纳了联盟风光新能源,使新能源占比增大,不用通过购买大量绿证来完成RPS考核;同时,风险系数越大,代表区域电网越想规避风险,电网通过调节电价,适时降低购买绿证情况,从而能获得更低的成本.

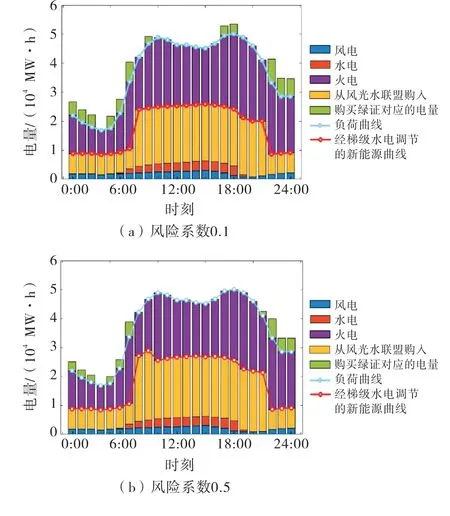
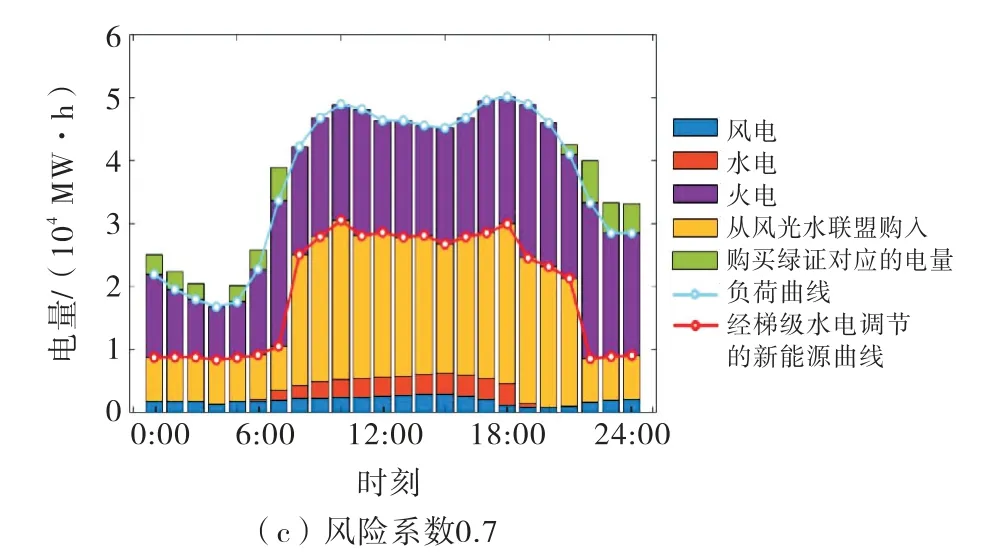
图7 上层电网能源组成

如图8～9所示,随着风险价值的增高,区域电网选择适时的提高电价来提高对风光水联盟的购买量,从而规避风险,同时能较好地降低成本.可以发现,在9:00～18:00等用电高峰期,随着风险系数的提高,区域电网适当地提高了电价,以此来提高此时段对风光水合作联盟电量的购买,从而达到规避风险降低成本的目的.

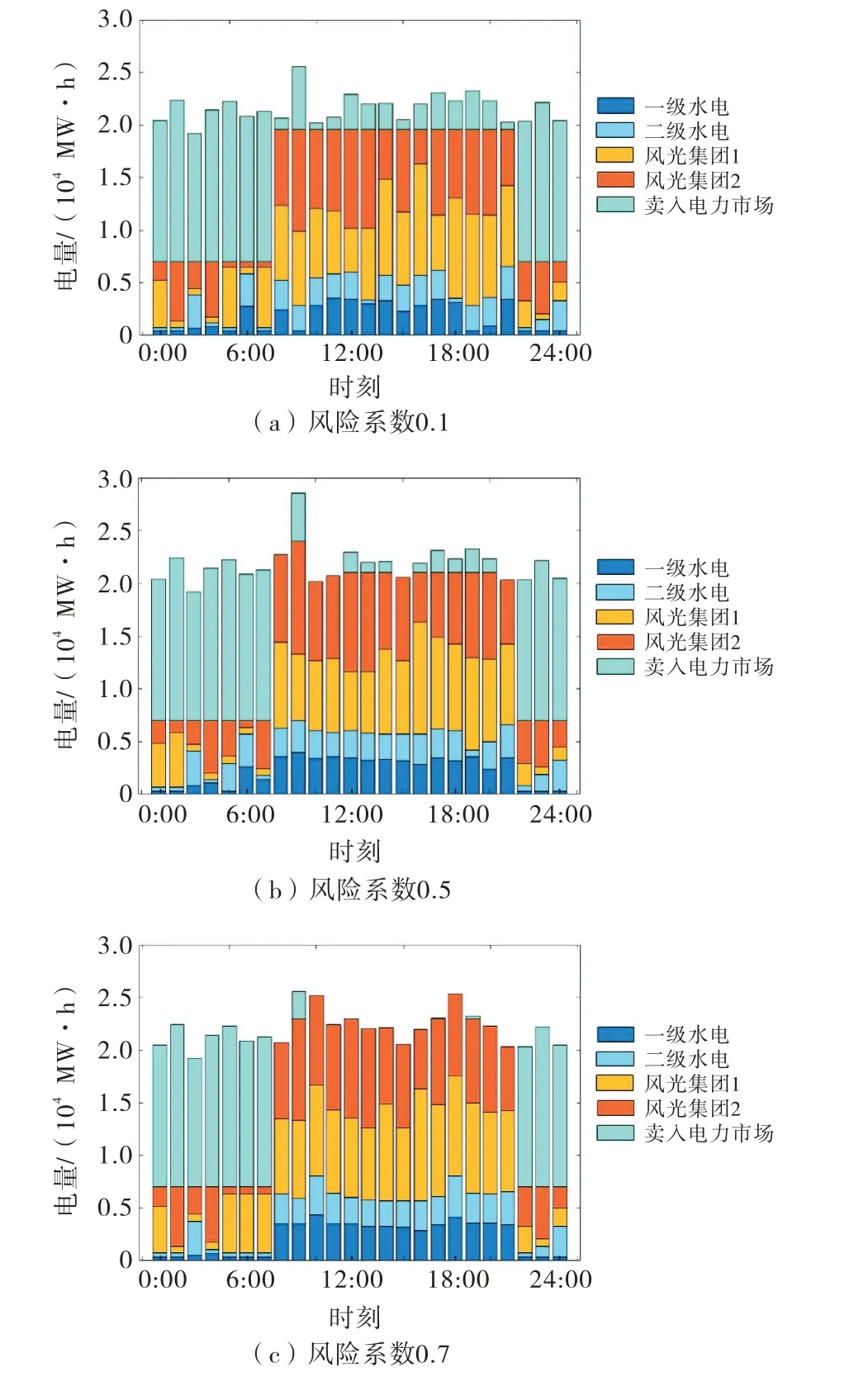
图8 下层合作联盟售电情况

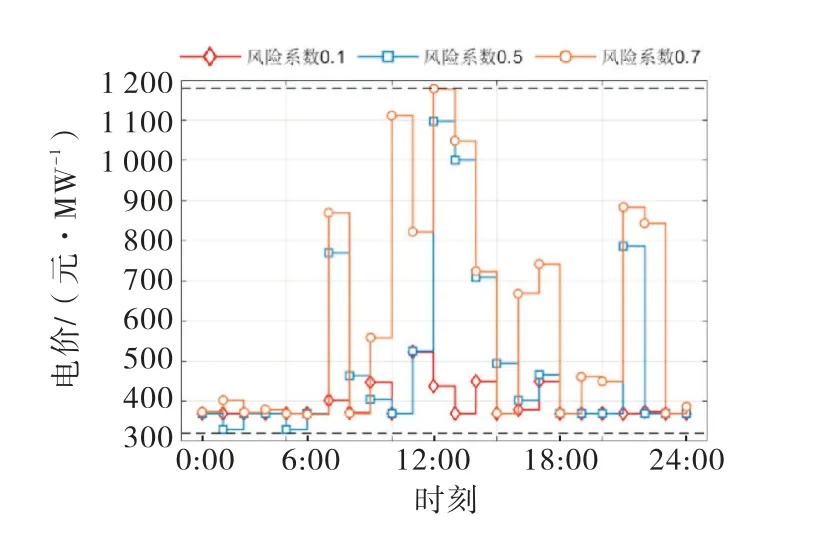
图9 电价随风险系数变化图

由表2 可以看出,区域电网从风光水联盟购电后,购买绿证的对应电量和受到惩罚的电量大大减少,降低了运行成本.随着条件风险系数的提高,风光水合作联盟的成本从6.21×1010元降至5.62×1010元,说明风险系数对电网的成本有着一定的影响,同时,随着风险系数的提高,对绿证的购买量也在降低.

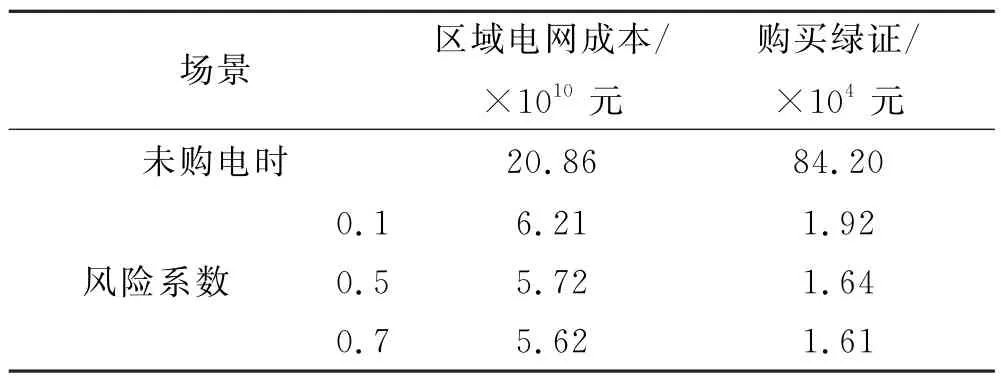
表2 区域电网成本与购买绿证随风险系数变化情况

5.2.3 非对称纳什议价利润分配结果分析

如图10～11所示,风光集团1在24 h的调度日对于梯级水电调节功率的最低补偿电价为1 221元,风光集团2在24 h的调度日对于梯级水电平抑波动的最低补偿电价为1 251.3元,均高于区域电网的电价1 178元,较高的出价是因为梯级水电更愿意帮助风光集团进行负荷跟踪.

图10 风光集团1对梯级水电补偿电价

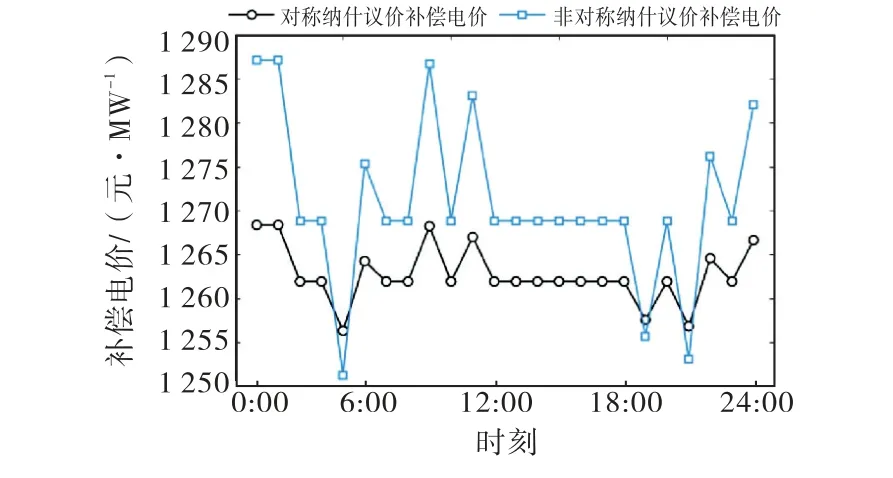
图11 风光集团2对梯级水电补偿电价

从表3可以看出,风光集团1、风光集团2和梯级水电在合作后利润均有提高.因此,合作联盟各主体更倾向于合作来进行售电,更有利于获取更大的利润.同时,通过非对称纳什议价计算可以看出,风光集团1的议价力小于风光集团2,梯级水电对风光集团1的调节功率要小于风光集团2 的调节功率,则此时,风光集团1的补偿电价有所降低,风光集团2的补偿电价有所升高,因此非对称纳什议价情况下计算的风光集团1的合作利润较纳什议价情况下计算的合作利润有所升高;反之,非对称纳什议价情况下计算的风光集团2的合作利润较纳什议价情况下计算的合作利润有所降低.可以看出,通过非对称纳什议价更能体现分配公平性.

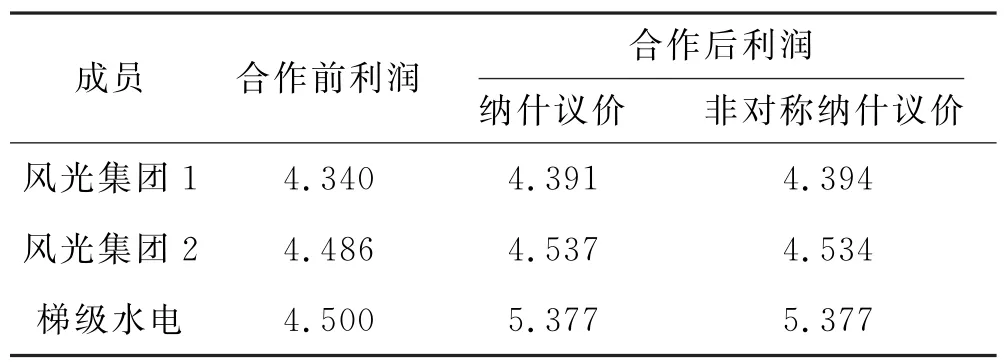
表3 合作前后各成员利润变化情况 (单位:107 元)

5.2.4 梯级水电调节功率内部优化分配

图12～13为梯级水电集团的两级电站的出力情况.原计划出力是指第二阶段“以水定电”优化调度结果,在此基础上叠加调节功率分配情况,即获得每个电站的实际出力调度曲线.

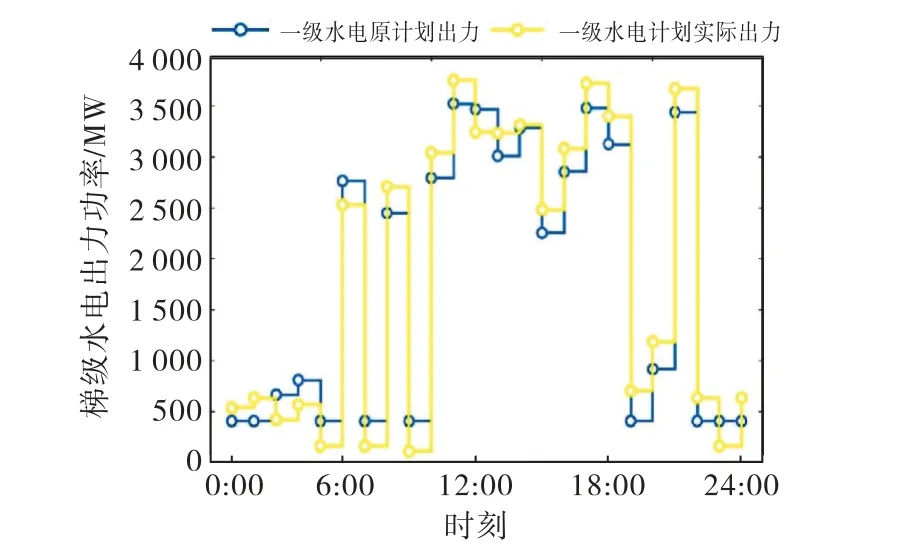
图12 一级水电功率变化情况

6 结 论

本文针对清洁型电网的大规模风光新能源消纳,提出了基于梯级水电调节的“电网负荷跟踪”调节方法及调节费用补偿机制,考虑风光不确定性的风光水网联合优化调度策略和基于非对称纳什议价的补偿费用公平分摊机制,实现调节费用的风光集团公平分摊疏导,促进新能源消纳.通过算例仿真验证了所提方法的有效性,得出主要结论如下:

1)提出的基于梯级水电调节的区域电网大规模风光新能源消纳策略,可实现大规模风光新能源入网的负荷跟踪调节,通过风光水联盟和区域电网的博弈优化,可实现大规模风光新能源的入网消纳,且满足区域电网的RPS考核及其经济运行,实现多参与主体的利益共赢;由风光集团承担水电调节费用的补偿,体现了“谁受益,谁承担”的原则,有利于保障水电调节利益,提高水电参与新能源调节的积极性.

2)提出的考虑风光不确定性的风光水网联合优化调度策略和基于非对称纳什议价的补偿费用公平分摊机制,可有效规避风光不确定性所带来的调度策略执行风险,实现调节费用的风光集团公平分摊补偿,促进新能源消纳.