基于卷积和抖动调制的音频数字水印算法

吴秋玲，曲爱妍，2，黄丹丹

(1.金陵科技学院 网络安全学院，江苏 南京 211169；2.中国人民解放军陆军工程大学 指挥控制工程学院，江苏 南京 210007)

0 引 言

音频数字水印技术[1-4]可分为时域和变换域两大类[5]。变换域算法通常具有较好的鲁棒性[6]，其变换方法包括离散小波变换[7，8]、离散傅里叶变换[9]和离散余弦变换[10]等。经过近二十几年的发展，音频水印算法的研究已出现较多成果，如混合域水印算法[11]、基于奇异值分解的鲁棒水印算法[12]、自适应水印算法[13]、基于量化思想的盲水印算法[14]，以及基于人工智能的水印算法[15]等，但大多数算法仍然存在透明性低，难以抵御同步攻击等不足之处。缺乏能够准确定位水印所在位置的同步机制是算法鲁棒性弱的重要原因之一。同步机制的实现方法主要有同步标识[16]、恒定水印[17]和自同步[18]等。此外，参数选取对算法整体性能的影响至关重要[19]，如何设置算法参数已成为水印算法研究中的难点问题。

针对上述问题，提出一种基于卷积和抖动调制的音频水印算法。以浊音帧中能量最大的小帧为标记设计同步机制，运用卷积运算设计了一个稳定的特征量，最后将水印以抖动调制的方式嵌入在特征量中。测试了水印嵌入频段、量化间隔以及子频段宽度3个关键参数对算法性能的影响，为算法的实际应用提供指导。

1 同步机制

浊音包含了音频的主要信息，对浊音数据修改太多，就会导致音频的听觉质量下降严重进而影响音频的使用价值[20]。针对音频的这一特点，以浊音帧中能量最大的小帧作为同步标记，以该标记周围固定范围内的音频数据作为承载水印的载体，设计了一种能够自动标识水印在音频中所处位置的同步机制。

将待嵌入的水印处理为L1行L2列的二进制矩阵，然后将其进行加密获得水印密文w(i，j)， 其中1≤i≤L1，1≤j≤L2。 将原始音频均匀分为L1段，搜索每个音频片段中能量最大的浊音帧，将该浊音帧分为多个长度为N1的小帧，并计算每个小帧的能量。以能量最大的小帧作为同步标记，在其周围选择a1+a2+1个小帧作为承载水印信息的区域。假设所选区域内的音频数据为xi(n)， 其中1≤n≤N1(a1+a2+1)， 根据同步标记在浊音帧中的位置，水印所在区域存在如下3种情况。

(1)若同步标记之前的小帧数量小于a1， 说明同步标记较为靠近该浊音帧的首端，则水印区域为从第一个小帧开始的连续a1+a2+1个小帧。

(2)若同步标记之后的小帧数量小于a2， 说明同步标记较为靠近该浊音帧的末端，则水印区域为位于末端的连续a1+a2+1个小帧。

(3)除上述两种情况之外，则以同步标记为基准，向前取a1个小帧，再向后选取a2个小帧。

2 基于卷积和抖动调制的音频水印算法设计

2.1 嵌入算法设计

离散余弦变换可在时域和频域间对信号进行相互转换，且离散余弦系数具有很强的“能量集中”特性和良好的去相关性，在多媒体信号处理领域获得广泛应用[15]。嵌入算法的原理框架如图1所示。

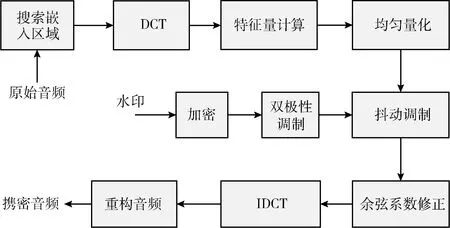
图1 嵌入算法原理

首先将原始音频均匀分为L1段，使用同步机制搜索水印的可嵌入区域，然后进行离散余弦变换、频段划分和特征量计算，使用均匀量化和抖动调制在每个音频片段中嵌入L2比特水印，最后修正余弦系数，并进行离散余弦逆变换以获得携带水印的携密音频。恒定水印是指在音频中寻找一个具有稳定特性的特征量，然后将水印嵌入到该特征量中来提升算法鲁棒性的一种设计方法[17]。如何设计特征量是恒定水印算法的关键问题。卷积运算可以看作将数字信号输入一个线性时不变系统后所得的输出信号，利用线性时不变系统的稳定特性可设计一个用于承载水印的特征量，具体设计方案描述如下。

将xi(n) 进行离散余弦变换得到系数Xi(k)， 其中1≤k≤N1×(a1+a2+1)。 从第b0根谱线开始，选择N2根谱线作为矩阵Yi的元素。从第b1根谱线开始，连续选取L2个子频段Z(i，j)， 每个频段含有N3根谱线。特征量CF(i，j)由Yi和Z(i，j)构成，如式(1)所示，其中⊗表示对Yi和Z(i，j)进行卷积运算，Mean() 表示对括号内的数据取平均值

(1)

对特征量CF(i，j)依次进行均匀量化和抖动调制可实现水印嵌入。以量化间隔δ对CF(i，j)进行均匀量化得到量化值CFQ(i，j)， 如式(2)所示，其中round() 表示对括号内的数据进行圆整

(2)

将水印密文w(i，j) 进行双极性调制获得w′(i，j)， 如式(3)所示

(3)

对特征量CFQ(i，j)进行抖动调制以实现将长度为L2比特的第i行水印密文嵌入到xi(n) 中，其嵌入规则如式(4)所示，其中CF′(i，j)是调制后携带有水印信息的特征量

(4)

假设嵌入水印后的子频段余弦系数为Z′(i，j)， 如式(5)所示，其中kj是第j个子频段余弦系数的放大倍数

Z′(i，j)=kjZ(i，j)

(5)

则由式(1)和式(5)可知，嵌入水印后的特征量CF′(i，j)可表达为式(6)

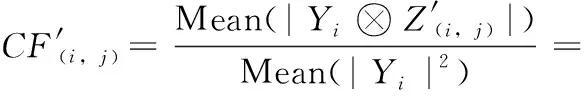
(6)

则放大倍数kj可由式(7)计算

(7)

可见，各个子频段中余弦系数的放大倍数kj由特征量、量化间隔以及水印的二进制取值共同决定。通过使用放大倍数kj对子频段的余弦系数进行修正即可获得抖动调制所需的特征量CF′(i，j)。

2.2 提取算法设计

提取算法是嵌入算法的逆过程。提取算法的原理框架如图2所示。首先将携密音频均匀的分为L1段，利用同步机制在每个音频片段中搜索水印的提取区域x′i(n)， 然后将x′i(n)进行离散余弦变换，并计算各个子频段的特征量CF′(i，j)， 再将其进行等间隔量化得到CF″(i，j)， 如式(8)所示

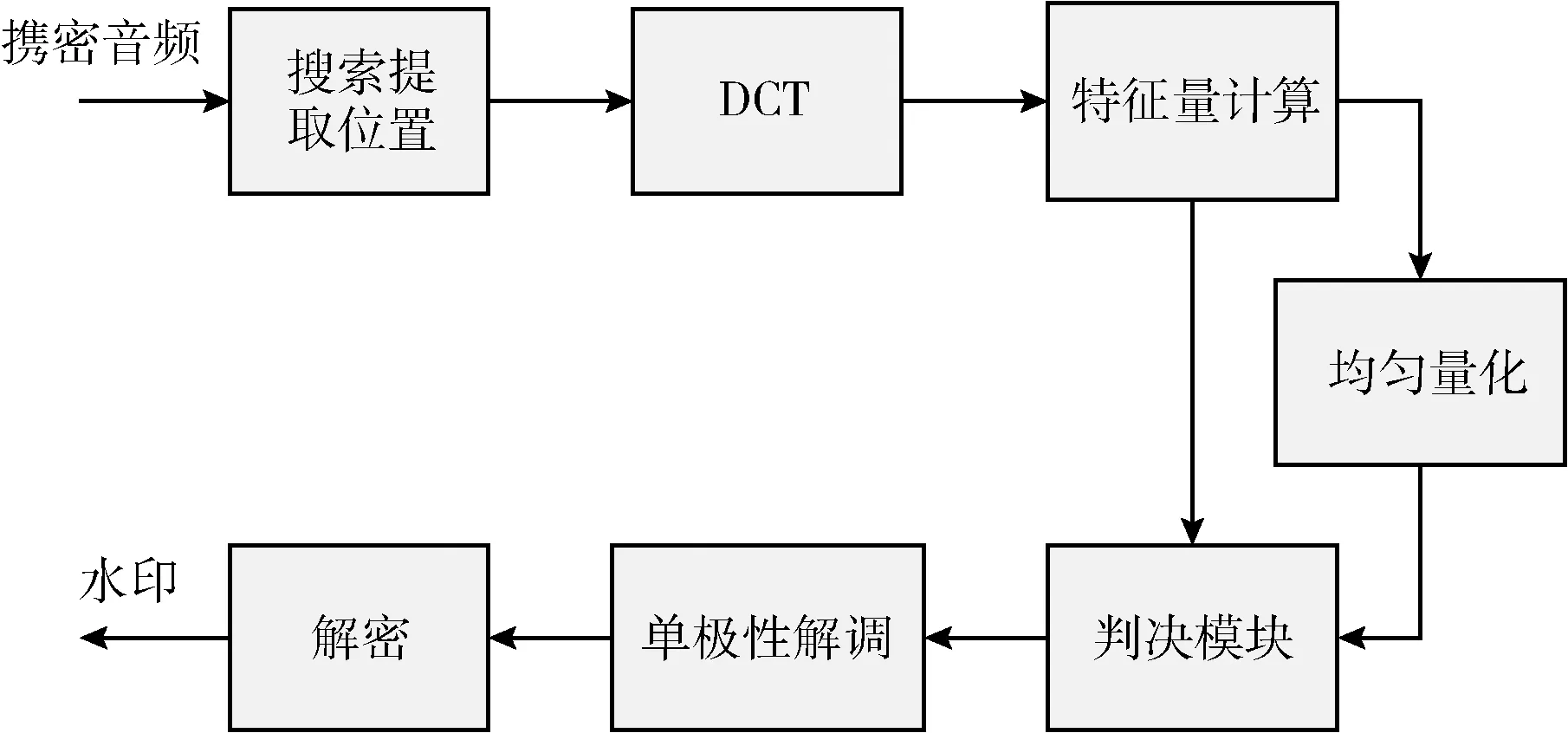
图2 提取算法原理

(8)

最后通过对比特征值CF′(i，j)与其量化值CF″(i，j)的大小来判断嵌入水印时的抖动方向，利用式(9)可将水印密文w″(i，j) 提取出来

(9)

3 算法实现

3.1 水印嵌入过程

水印嵌入步骤描述如下：

步骤1 将水印进行加密和双极性调制等预处理，得到L1行L2的二进制矩阵w′(i，j)。

步骤2 将原始音频分为L1段，在每个音频片段中使用同步机制搜索能够携带水印的区域xi(n)。

步骤3 将xi(n) 进行离散余弦变换得到Xi(k)。

步骤4 从第b0根谱线开始选择N2根谱线构建Yi。

步骤5 从第b1根谱线开始连续选取L2个子频段Z(i，j)， 每个频段含有N3根谱线。

步骤6 利用式(1)计算每个子频段的CF(i，j)。

步骤7 利用式(2)对CF(i，j)进行均匀量化。

步骤8 利用式(4)计算CF′(i，j)。

步骤9 利用式(7)计算放大倍数kj。

步骤10 利用式(5)计算携带有水印的Z′(i，j)。

步骤11 用Z′(i，j)替换Xi(k) 中相应位置上的数据得到携带有水印的余弦系数X′i(k)。

步骤12 对X′i(k)进行离散余弦逆变换，重构该音频片段的时域数据。

步骤13 重复步骤3到步骤12，直至将所有水印信息嵌入至全部音频片段中。

步骤14 将所有音频片段连接起来得到携密音频。

3.2 水印提取过程

水印提取步骤描述如下：

步骤1 将携密音频分为L1段，在每个音频片段中使用同步机制搜索水印的提取区域x′i(n)。

步骤2 将x′i(n)进行离散余弦变换得到X′i(k)。

步骤3 从第b0根谱线开始选择N2根谱线构建Y′i。

步骤4 从第b1根谱线开始连续选取L2个子频段Z′(i，j)， 每个频段含有N3根谱线。

步骤5 计算各个子频段的特征量CF′(i，j)。

步骤6 以δ对CF′(i，j)进行量化得到CF″(i，j)。

步骤7 根据式(9)从x′i(n)中提取L2比特水印。

步骤8 重复步骤2到步骤7，直至将所有音频片段中的水印密文全部提取出来。

步骤9 将水印密文解密得到可识别的水印信息。

4 算法参数设置

本小节测试水印嵌入频段、量化间隔以及子频段宽度3项关键参数对算法性能的影响，为该算法在实际应用中的参数设置提供参考。本次测试实验中，算法的透明性和鲁棒性分别用信噪比(signal-to-noise ratio，SNR)和误码率(bit error rate，BER)来定量评价。SNR的计算公式如式(10)所示，其中x(m) 和x′(m) 分别表示原始音频和携密音频的采样值，M是x(m) 含有的总采样点个数。SNR的值越大，表明音频质量受损越小，则算法的透明性越好。误码率的计算如式(11)所示，BER越小，表明水印提取的成功率越高，则算法的鲁棒性越强

(10)

(11)

以20条WAV格式的音频作为研究对象，时长均为64 s，采样率为44.1 kHz，量化位数为16 bit。待测水印为两幅尺寸分别为64×43和64×86的图片，如图3所示。算法参数设置为：N1=8，a1=171，a2=340， 其它关键参数待测试。实验环境为：64位 Microsoft Windows 10操作系统、编程语言为Matlab 2016R、音频剪辑工具为Cool Edit Pro。

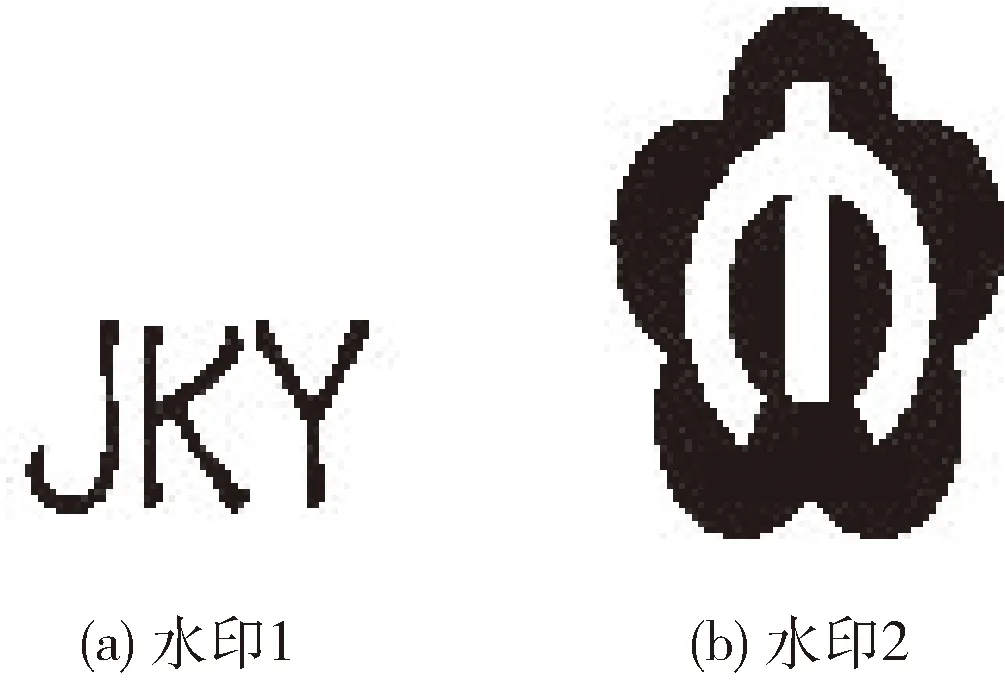
图3 待测试水印

4.1 水印嵌入频段

由嵌入原理可知，矩阵Yi和Z(i，j)在整个算法设计中至关重要，由于二者均取自于余弦系数Xi(k)， 因此其位置参数b0和b1的选取对算法性能具有重要影响。将水印2嵌入到音频中，然后对其进行20 dB的白噪声攻击，分别测量b0取值为4、8和12这3种情况下，b1在[50，3000]之间取值时算法的透明性和鲁棒性。SNR和BER的测试结果如图4所示，其中δ=0.4，N2=4，N3=4， 谱线间隔Δf为5.376 Hz。

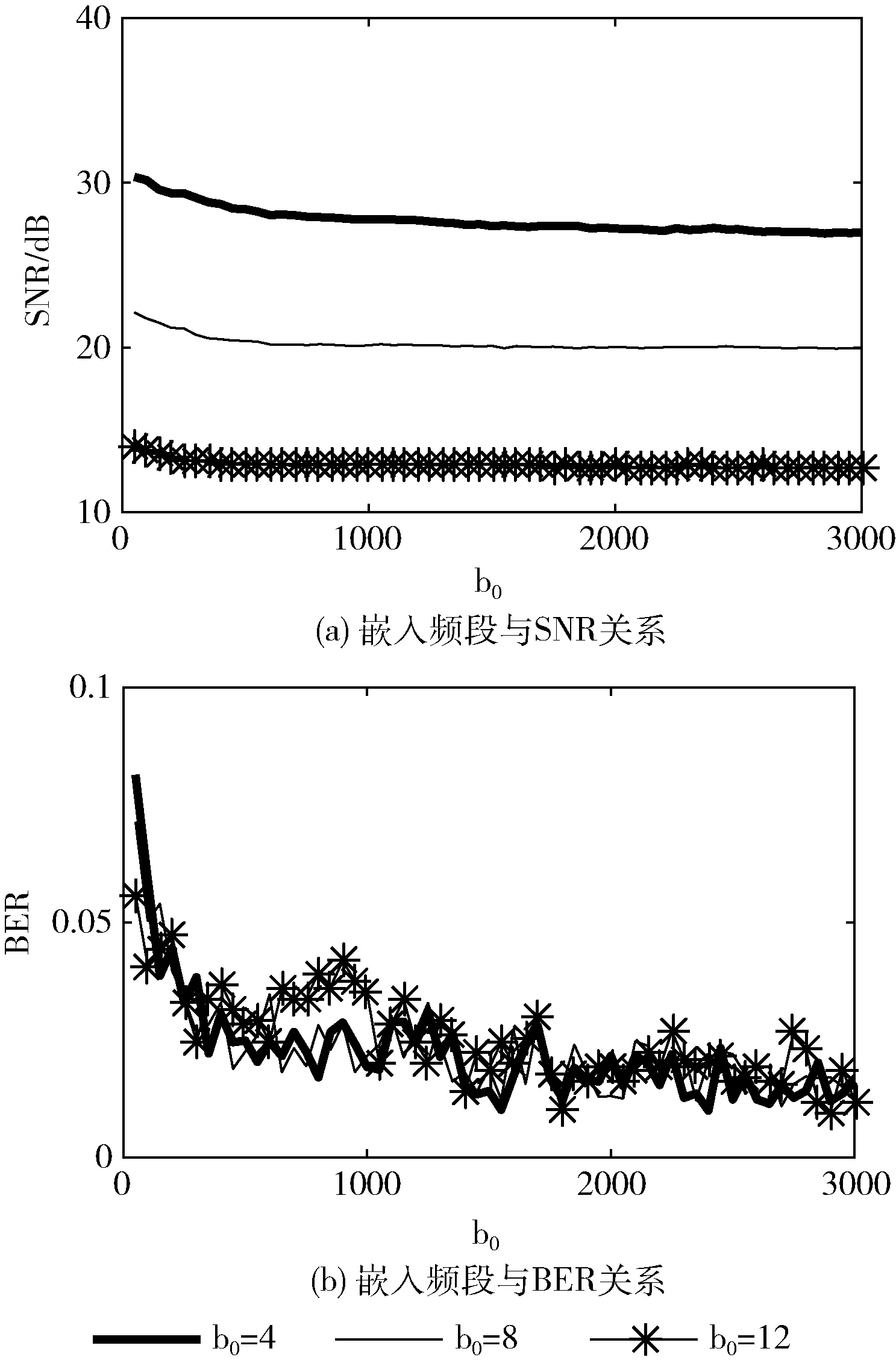
图4 嵌入频段对算法性能的影响

由图4可见，b0为4时，SNR取值远高于另外两条曲线，且对应的BER曲线最低，说明Yi处于低频段时，算法具有良好的透明性和强鲁棒性。随着b1逐渐增大，携带水印的Z(i，j)逐渐远离Yi， SNR和BER曲线均呈缓慢下降趋势，说明Z(i，j)所处频率越高，算法的透明性有所下降，对20 dB白噪声的抵抗能力略有增强。

4.2 量化间隔

在均匀量化和抖动调制中，量化间隔δ是一个重要参数。δ在[0.1，4]之间取值时，算法的透明性和鲁棒性的测试结果如图5所示。

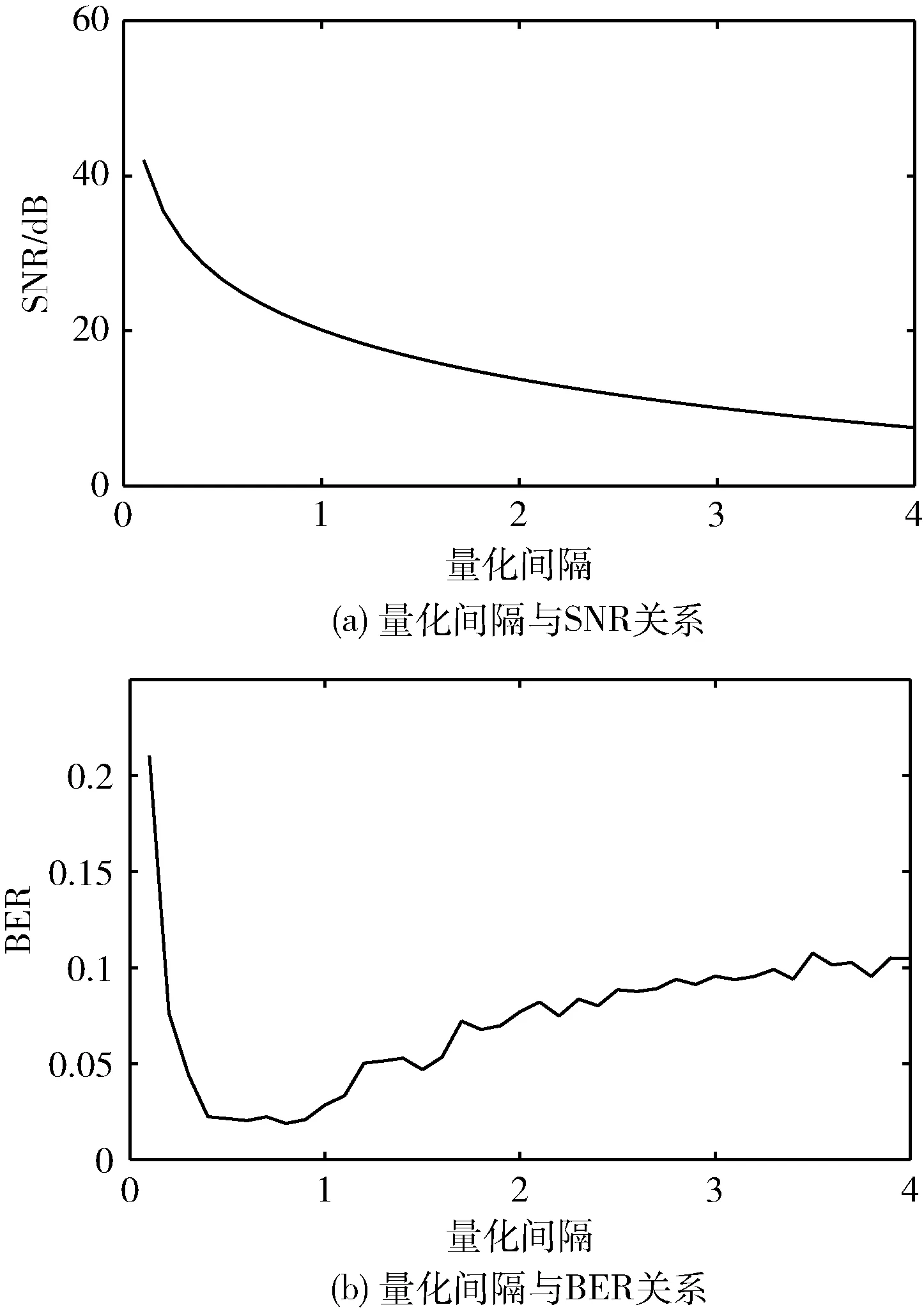
图5 量化间隔对算法性能的影响

本次实验中，b0=4，b1=400， 其它实验参数与4.1节相同。从实验结果可知，随着量化间隔的增大，SNR曲线逐渐下降，说明透明性越来越低，BER曲线在δ处于[0.4，0.9]之间时达到谷底，说明δ在该区间内取值可使该算法获得较强的鲁棒性。

4.3 子频段宽度

由嵌入原理可知，N2和N3分别是矩阵Yi和子频段的长度，与参数b1、L2以及Δf共同决定了嵌入区域的频段宽度 [b1Δf，(b1+N3L2)Δf]。 对携密音频分别进行20 dB的白噪声和4 kHz的低通滤波攻击，测量N2取值为4、8和12。这3种情况下，N3在[2，20]之间取值时算法的透明性和鲁棒性，测试结果如图6所示。其它实验参数和4.2节相同。由图6(a)、图6(b)可知，N2取4时，其SNR曲线远高于另外两条曲线，且对应的BER曲线最低，说明Yi频段较窄时，算法具有较高的透明性和鲁棒性。

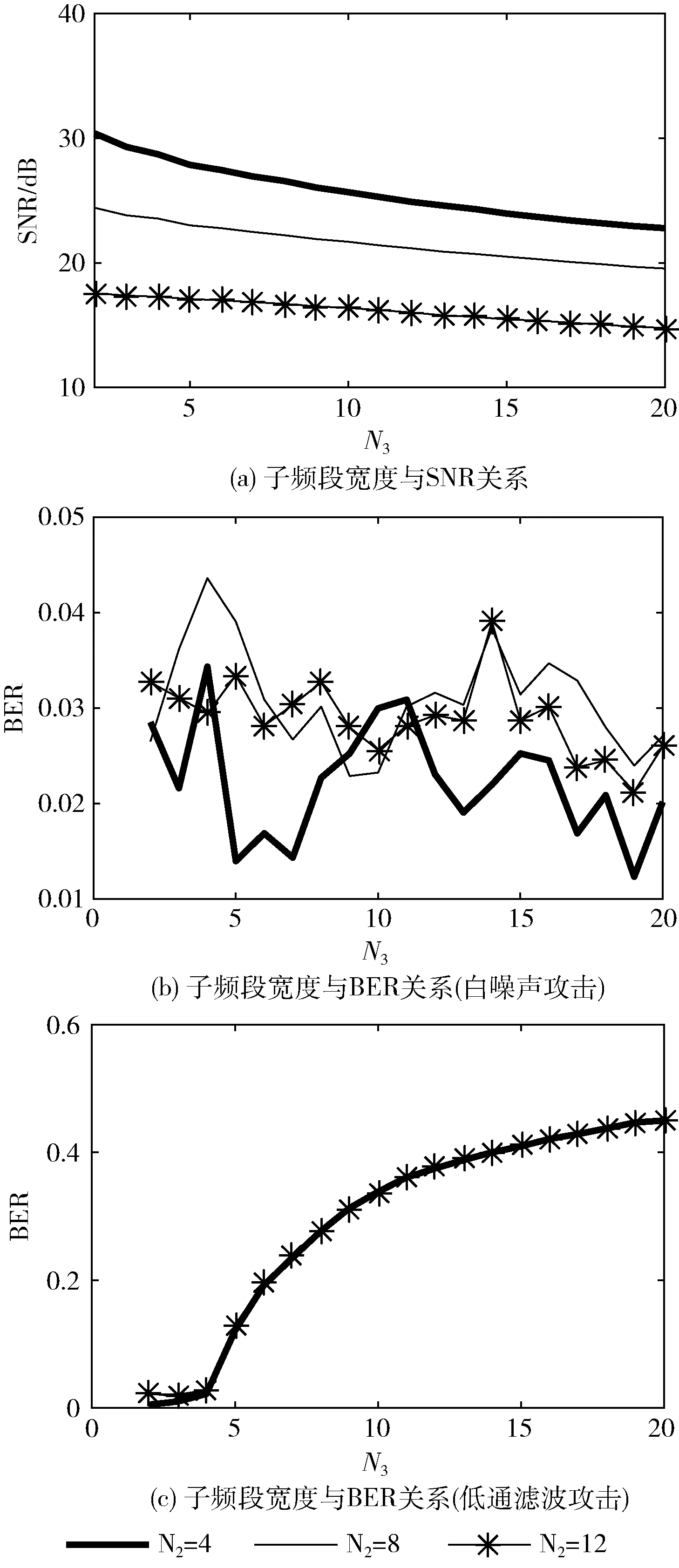
图6 子频段宽度对算法性能的影响

由图6(b)可知，N3在[2，20]之间取值时，误码率变化非常平缓，说明子频段宽度对白噪声攻击不敏感。在图6(c)中，当N3的取值大于4时，误码率显著上升，说明子频段宽度对算法抵御低通滤波攻击的能力具有重要影响。

5 算法性能评估

本小节测试算法的隐藏容量、透明性、鲁棒性和复杂性，采用SNR和音频质量感知评估标准的客观差异等级(object difference grade，ODG)定量衡量算法的透明性，采用BER和相关系数(normalized correlation，NC)评价算法的鲁棒性。NC的计算公式如式(12)所示，NC越接近于1，表明所提取的水印与原始水印相比相似性越大，则算法的鲁棒性越强。隐藏容量Cap用单位时间内音频所能携带的水印的比特数量来衡量

(12)

参考上一小节的参数测试结果，本小节测试中将算法参数优选为：δ=0.4，N2=N3=4，b0=4，b1=400。 表1列出了各项性能的平均实验结果，包括SNR(dB)、ODG、BER(%)、NC和Cap(bps)，并在相同实验条件下，将所得结果与文献[2]、文献[14]、文献[17]和文献[20]进行对比分析，以评估算法的整体性能。

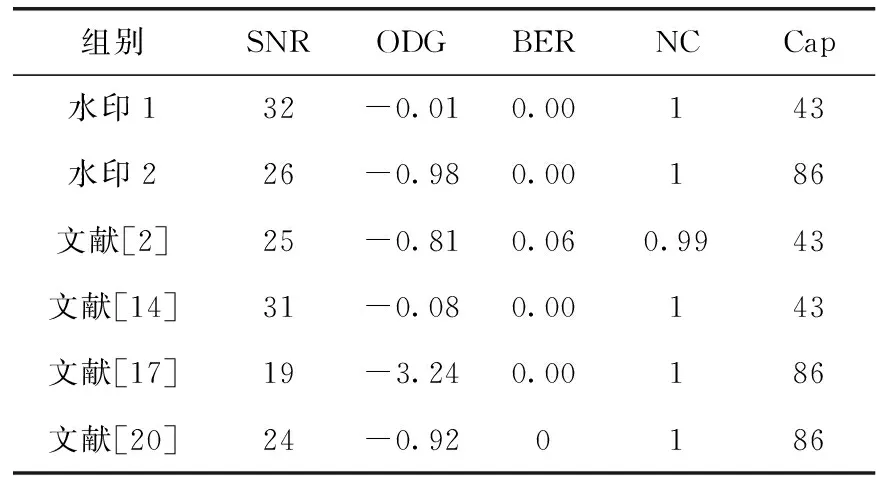
表1 平均实验数据(无攻击)

5.1 隐藏容量

由嵌入和提取原理可知，Z(i，j)中子频段的个数决定了算法的隐藏容量。该算法的最大隐藏容量如式(13)所示，其中T是音频的总时长。由公式计算可知，该算法在隐藏水印1时，其隐藏容量为43 bps，在隐藏水印2时，隐藏容量为86 bps

(13)

5.2 透明性

由表1中数据可知，在隐藏水印1时，该算法的SNR达到32 dB，ODG为-0.01，透明性优于具有相同隐藏容量的文献[2]和文献[14]中的算法。在隐藏水印2时，隐藏容量变大，SNR和ODG值都有所降低，但音频仍保持良好的听觉质量，且优于文献[17]和文献[20]中的算法。原始音频和携密音频的波形图和语谱图分别如图7和图8所示(为显示细节，仅截取3 s的音频片段)，水印嵌入前后音频的波形和频谱图均没有发生明显变化。

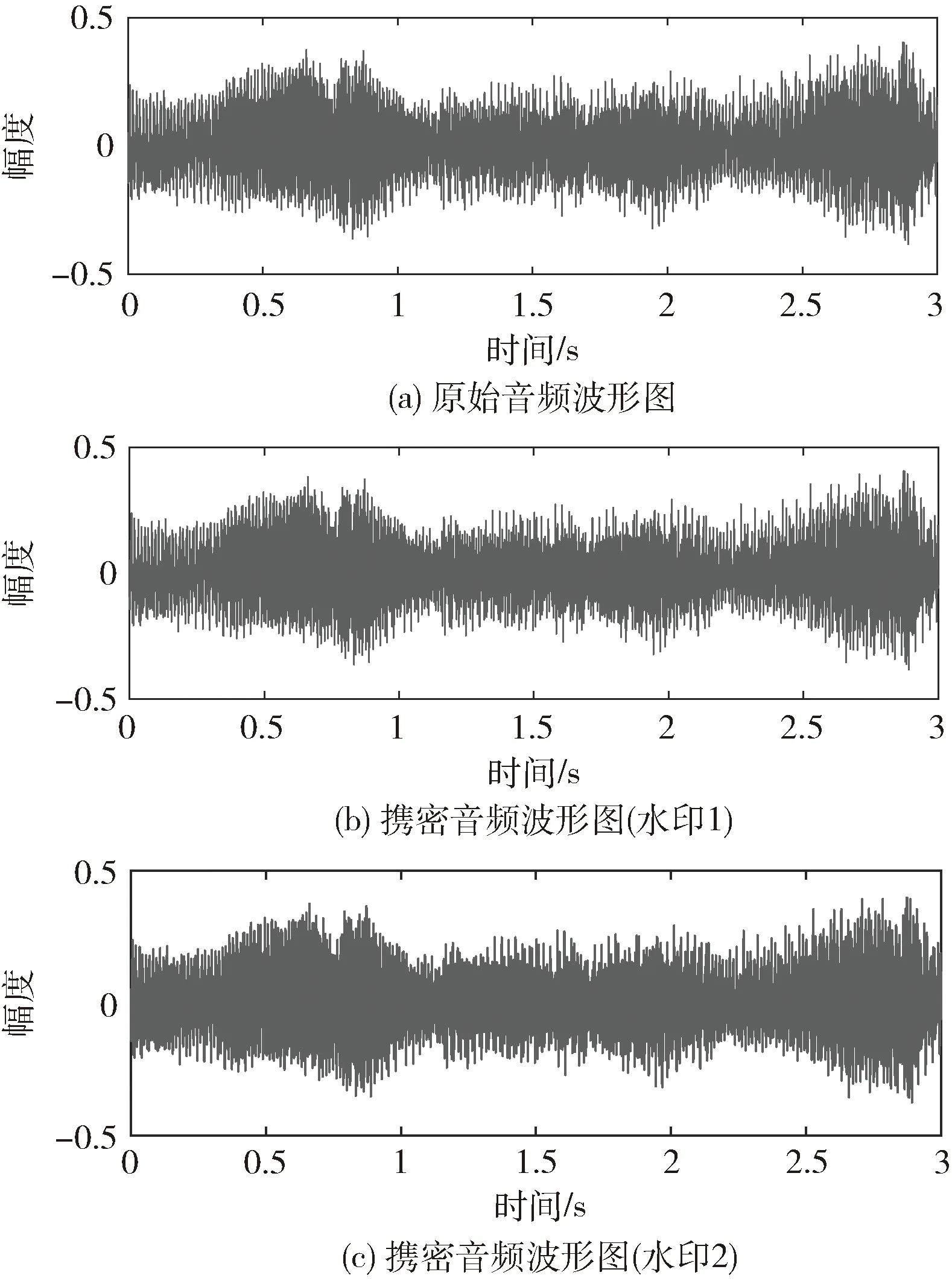
图7 音频波形对比

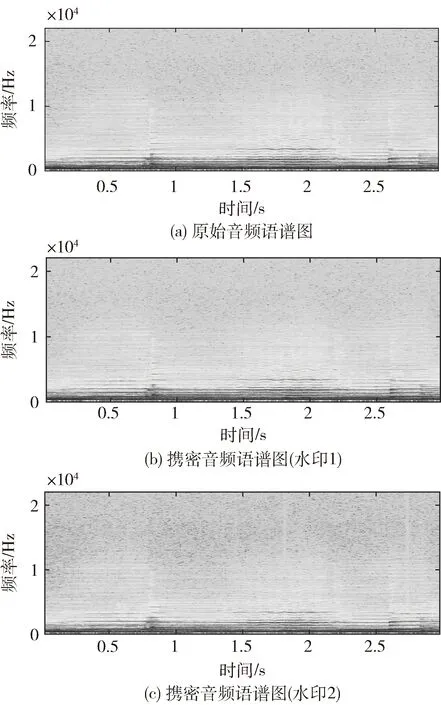
图8 音频语谱对比

该算法具有较好透明性的原因一方面在于水印仅嵌入在有限的窄频段上，且可以通过设置位置参数b1和N3来调节嵌入区域的位置，另一方面在于该算法仅通过对特征量进行抖动调制来修改余弦系数，因此对音频数据的损伤较小。

5.3 鲁棒性

表1数据显示，在无攻击情况下，两组实验的BER都是0，NC均为1，这说明该算法在无攻击情况下可将水印清晰提取出来。表2为本次测试的攻击类型，共有12种攻击。对携密音频进行攻击后，将相同类型的攻击下计算所得的BER(%)取均值列于表3中，将NC值最接近平均值的水印图片以及对应的NC列于图9和图10中。

表2 攻击类型

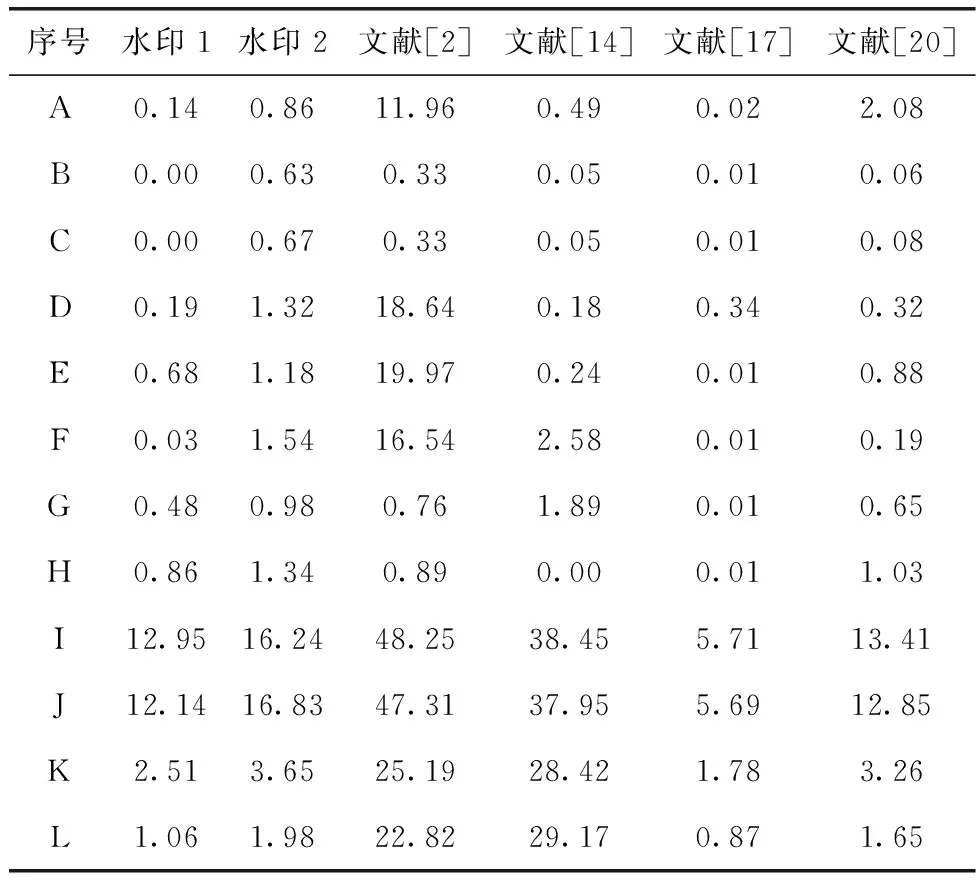
表3 鲁棒性测试

图9 水印1的提取结果

图10 水印2的提取结果

由实验结果可知，该算法对噪声污染、回声干扰、幅度缩放、MP3压缩、低通滤波、重采样和重量化均表现出很强的鲁棒性，BER低于1.34%，所提取的水印图片与原始水印相比相似度在0.96以上。在抖动和随意剪辑两种攻击测试中，BER均低于3.65%，所提取的水印图片与原始水印相比相似度均在0.96以上，表明该算法能够较好抵御这两种同步攻击。

在时间拉伸和时间缩短两种攻击测试中，BER较高，所提取图片被破坏严重，其原因是水印嵌入区域在时间缩放攻击中绝对位置发生漂移，在提取水印时，同步机制在追踪提取区域时也随之产生偏差，但从图9和图10的测试结果来看，所提取的水印图片仍然能够较为清晰分辨出主要信息。

在4 kHz的低通滤波攻击中，水印1被嵌入在2.15 kHz至3.07 kHz的频段上，水印2被嵌入在2.15 kHz至3.99 kHz频率范围内，由于3.99 kHz比3.07 kHz更接近于低通滤波器的截止频率，因此所提取的水印2比水印1的误码率高。

在相同隐藏容量下，水印1的各项测试结果中SNR、ODG和BER均优于文献[2]和文献[14]中所提算法，水印2的测试结果优于文献[20]中所提算法，虽然鲁棒性稍逊于文献[17]中的算法，但文献[17]中算法的透明性非常低，其信噪比只有19 dB。

5.4 复杂性

复杂性是评估水印算法性能的重要指标，可通过计算程序运行时间来衡量。表4列出了5种算法在嵌入和提取水印2时的平均运行时间。

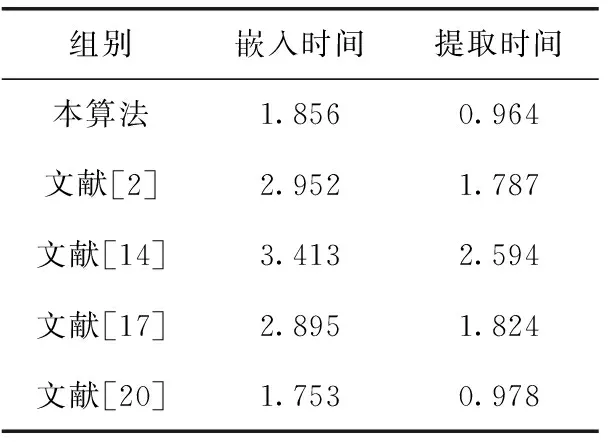
表4 运行时间/s

从实验结果来看，该算法的水印嵌入时间要高于提取时间，且平均所耗时间基本与其它4种算法接近。嵌入算法在浊音帧中搜索嵌入区域的平均时间是0.038 ms，提取算法在搜索提取区域时所耗平均时间为0.036 ms，表明本算法未增加时间成本，因此复杂度不高，便于实际应用。

6 结束语

本文算法使用同步机制定位水印位置，通过抖动调制对卷积运算所构建的稳定特征量进行微小修改即可将水印嵌入至音频中，具有良好的鲁棒性和透明性。该算法无需原始音频的参与，通过判断特征量的抖动方向就可获得水印的二进制取值，具有盲提取能力。实验结果表明，该算法能够抵御多种攻击类型，在两种隐藏容量下均表现出较高的透明性和强鲁棒性。

今后，将进一步研究如何提升算法抵御时间缩放攻击的能力，以及算法参数的自适应设置问题。