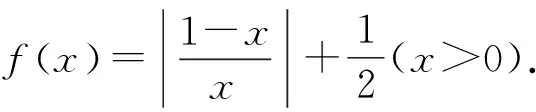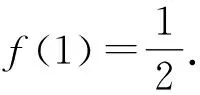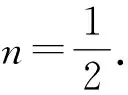巧借齐一次分式函数模型解决数学问题
李鑫斌
(福建省龙海第一中学,福建 龙海 363100)

1 在指数函数中的应用



图1 的图象

2 对数函数中的应用



图2 的图象

由已知可得loga(a2-5a+9) 当a>1时,f(x)∈[loga3,loga5],则loga(a2-5a+9) 当0 所以a∈(0,1)∪(2,3). 图3 的图象 故d=2.则an=2n-1,Sn=n2. 图4 的图象 解析设ΔMF1F2内切圆的半径为r,则 图5 的图象 图6 的图象 图7 的图象 图8 的图象3 在三角函数中的应用




4 在数列中的应用


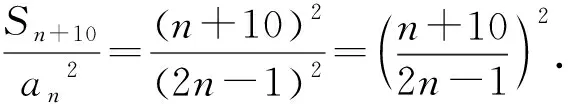



5 在圆锥曲线中的应用





6 综合性问题