一种星载相对测量设备的在轨标定方法

黄业平,王 瑞,邓武东,郭正勇,刘 政

(1.上海卫星工程研究所,上海 201109;2.上海航天控制技术研究所,上海 201109)

0 引言

随着太空技术的发展,航天工程已逐步从传统的遥感、通信、导航等任务,向在轨服务、在轨装配、编队飞行等新型任务拓展[1]。这些航天任务涉及到一项共性技术,即高精度相对测量和相对导航技术。

高精度相对测量是实现高精度相对导航的前提,测量设备早期以微波雷达为主。20 世纪60年代初,美国为双子星座号飞船研制的L波段雷达采用脉冲测距和单脉冲比幅技术实现了目标跟踪[2-3]。近年来,随着光学技术、特别是激光技术的发展,光学相机、激光雷达等新型测量设备开始用于高精度相对测量。另外,根据测量设备特点,可采用分段使用策略实现全航程高精度测量,如远距离采用微波雷达,近距离采用激光雷达和光学相机等。

发射前,航天器相对测量、姿态测量、有效载荷等设备通过地面装调和精度测量实现基准坐标系的统一。但航天器发射后,由于受主动段振动、在轨重力释放、热变形等因素的影响,各设备的测量坐标系与基准坐标系之间、不同设备的基准坐标系之间会出现一定偏移。如果不对这些偏移进行校准,即便测量设备及星敏感器的测量精度再高,也无法准确获取目标的相对距离和角度信息,从而降低航天器相对导航精度,影响编队飞行。本文提出一种基于全球卫星导航系统(global navigation satellite system,GNSS)差分定位数据的星载相对测量设备在轨标定方法,对影响其在轨标定精度的主要误差项进行分析,明确可实现的在轨标定精度水平,并结合在轨数据验证该方法的正确性和有效性。

1 GNSS差分定位技术

随着GNSS 在航天领域应用研究的不断深入,GNSS接收机在应用灵活性、系统精度、体积、重量、功耗及成本等方面的优势日益被各国所重视,并被广泛应用于航天器的导航和测控设备中。一般情况下,美国全球定位系统(GPS)的单点定位精度约为10 m,我国北斗卫星导航系统的单点定位精度可达5 m。单点定位精度显然无法满足航天器的高精度定位需求[4],因此GNSS差分定位技术应运而生。

GNSS差分定位是指两航天器利用GNSS接收机同步跟踪、接收导航卫星信号,采集测量数据,通过航天器间链路进行数据交换或者将数据同步传输至地面,进行数据差分处理,降低测量数据误差,提高定位精度。GNSS差分定位技术使定位精度提高了1～2个数量级[4-5],并具有处理方法简单等优点,因此得到了广泛应用并且发展迅速。

GNSS差分定位可以采用位置差分、伪距差分和载波相位差分三种方法[4,6]。与位置差分定位和伪距差分定位相比,载波相位差分定位精度更高,可达厘米量级甚至毫米量级[4,6-8],能够满足星载相对测量设备在轨标定的需求。

2 在轨标定方法

2.1 坐标系与测量数据定义

通常情况下,星载相对测量设备的测量坐标系建立在探测器上,基准坐标系建立在安装平面上。通过地面高精度测量,可获取两个坐标系的相对关系,将测量数据由测量坐标系转换至基准坐标系。

在轨应用时,需根据相对测量设备在卫星上的安装位置矩阵和卫星姿态测量数据,将测量数据由设备基准坐标系转换至卫星本体坐标系和轨道坐标系。

目标测量数据一般采用极坐标形式表示,转换时先进行俯仰向转换,再进行方位向转换。目标测量数据在测量设备基准坐标系oclxclyclzcl中的定义如图1所示。其中,xcl轴指向卫星飞行方向,ycl轴指向卫星轨道法线反方向,zcl轴根据右手法则确定,t为待测目标,t′为目标在oclxclzcl平面上的投影,Lcl,t为目标测量相对距离,θcl,t为目标测量俯仰角,ψcl,t为目标测量方位角。

图1 目标相对测量数据在设备基准坐标系中的定义

2.2 相对测量矢量与GNSS差分定位关系分析

A 星对B星进行相对测量,A 星对B星的相对测量矢量与GNSS 差分定位的关系如图2所示。

(2) 为规避卡机事故，在类似复杂地质条件下的隧洞掘进中，尤其是在高寒缺氧、大埋深、大断层、长隧洞TBM施工中，需做到“短进尺、强支护”，采用先进的超前物探方法，超前预报，时刻监测围岩变化情况，超前支护。

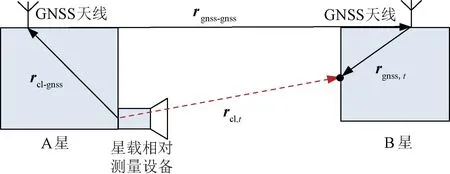
图2 相对测量矢量与GNSS差分定位的关系

图2中:rcl,t为两星相对测量矢量,由A 星相对测量设备的基准坐标系原点指向B 星朝向A 星的侧面形心;rcl-gnss为A 星GNSS天线安装位置矢量,由A 星的相对测量设备基准坐标系原点指向A 星GNSS接收天线相位中心;rgnss,t为B星GNSS天线安装位置矢量,由B星GNSS接收天线相位中心指向B星侧面形心;rgnss-gnss为两星GNSS天线间的相对位置矢量,由A 星GNSS接收天线相位中心指向B 星GNSS接收天线相位中心。

两星相对测量矢量rcl,t可表示为

式中:xcl,ycl,zcl分别为相对测量矢量rcl,t在A星相对测量设备基准坐标系中的三个坐标分量。

进行差分定位时,先根据GNSS数据分别确定两星GNSS天线绝对位置,再采用差分定位技术确定两星GNSS 天线间的高精度相对位置矢量rgnss-gnss,因此rgnss-gnss又称为GNSS 差分定位矢量。两星GNSS 天线安装位置矢量rcl-gnss,rgnss,t可通过地面高精度测量获取。

综上,两星的相对测量矢量rcl,t可表示为

2.3 坐标系统一

式(2)中的四个矢量分别定义在不同坐标系下,需将其统一转换至轨道坐标系。转换方程为

式中:Aab-o为A 星本体坐标系相对于轨道坐标系的转移矩阵;Acl-ab为A 星相对测量设备基准坐标系相对于A 星本体坐标系的转移矩阵;Abb-o为B星本体坐标系相对于轨道坐标系的转移矩阵。

2.4 在轨标定

式中:(·)-1表示矩阵求逆运算。

由式(4)可知:等式左侧的Δrcl,t为待标定的相对测量误差矢量;等式右侧为转换至轨道坐标系的两星GNSS差分定位矢量、包含姿态信息的两星GNSS天线安装位置矢量及两星的相对测量矢量,这些参数均为已知量。通过采集多组数据求均值的方法实现相对测量误差矢量标定。相对测量误差矢量计算公式为

式中:n为数据采集数;(·)i表示第i次数据采集。

3 在轨标定精度分析

GNSS 差分定位矢量、含姿态信息的两星GNSS天线安装位置矢量及两星的相对测量矢量数据均存在一定误差,这会影响A 星相对测量误差的标定精度。对式(3)进行一阶展开,可得到

其中

式中:δ1为两星GNSS差分定位误差引起的在轨标定误差矢量;Δrgnss-gnss为轨道坐标系下两星GNSS差分定位误差矢量;δ2为两星GNSS天线安装位置误差引起的在轨标定误差矢量;Δrcl-gnss为A 星本体坐标系下GNSS天线安装位置误差矢量;Δrgnss,t为B星本体坐标系下GNSS天线安装位置误差矢量;δ3为A 星姿态误差引起的在轨标定误差矢量;ΔAab-o为A 星姿态误差矢量;E为单位矩阵;δ4为B星姿态误差引起的在轨标定误差矢量;ΔAbb-o为B星姿态误差矢量;δ5为A星相对测量设备和本体坐标系基准误差引起的在轨标定误差矢量;ΔAcl-ab为A 星相对测量设备和本体坐标系基准误差矢量。

通过对误差项的方向性进行分析,可以得到以下结论。

影响星载相对测量设备距离测量值标定精度的主要误差项为δ1和δ2。采用载波相位差分定位技术可将δ1控制在厘米量级[4,6-8],同时δ2也可控制在厘米量级。综上,星载相对测量设备距离测量值的标定精度优于5 cm。

影响星载相对测量设备角度测量值标定精度的主要误差项为δ1～δ5。当两星相距10 km 以上时,可将GNSS差分定位误差和GNSS天线安装位置误差带来的在轨标定角度误差控制在0.000 1°以内;采用高精度星敏感器,可实现角秒量级的姿态测量精度;采用共基准安装、精密温度控制等方法,可将相对测量设备与星敏感器的基准角度误差控制在0.001°以内。综上,星载相对测量设备角度测量值的标定精度优于0.002°。

4 在轨标定验证

A 星上的相对测量设备由测量前端和二维指向机构组成,设备与星敏感器共同安装于同一块高稳定基板上。在轨使用时,受主动段振动以及在轨重力释放等因素影响,设备测量值存在一个常值误差。同时,太阳光从不同角度照射二维指向机构,引起机构热变形,导致设备测量值存在一个和轨道周期相关的低频角度误差。A 星安装有双频双模GNSS接收机,与同轨安装有双频双模GNSS接收机的B星开展了在轨标定。

在轨标定分为常值误差标定和低频角度误差标定两步。首先,利用GNSS差分定位数据标定相对测量设备的常值误差。相对测量设备常值误差在轨标定情况如图3所示。

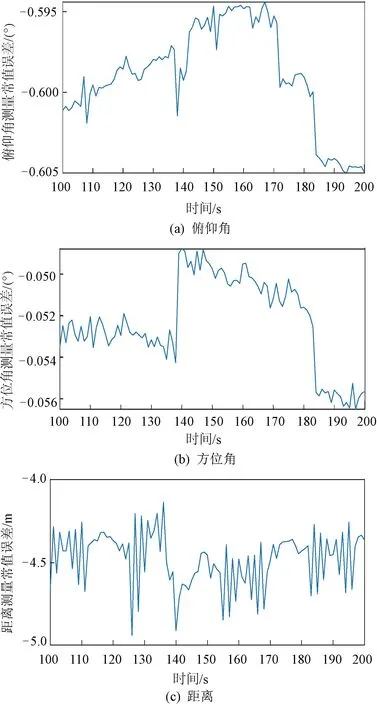
图3 相对测量设备常值误差在轨标定情况

由图3可得,相对测量设备俯仰角测量常值误差为-0.600°,方位角测量常值误差为-0.053°,距离测量常值误差为-4.5 m。

然后,利用多天多轨数据标定相对测量设备的低频角度误差。采用10阶多项式对多天多轨数据进行拟合,相对测量设备低频角度误差与面内太阳角的关系曲线如图4所示。

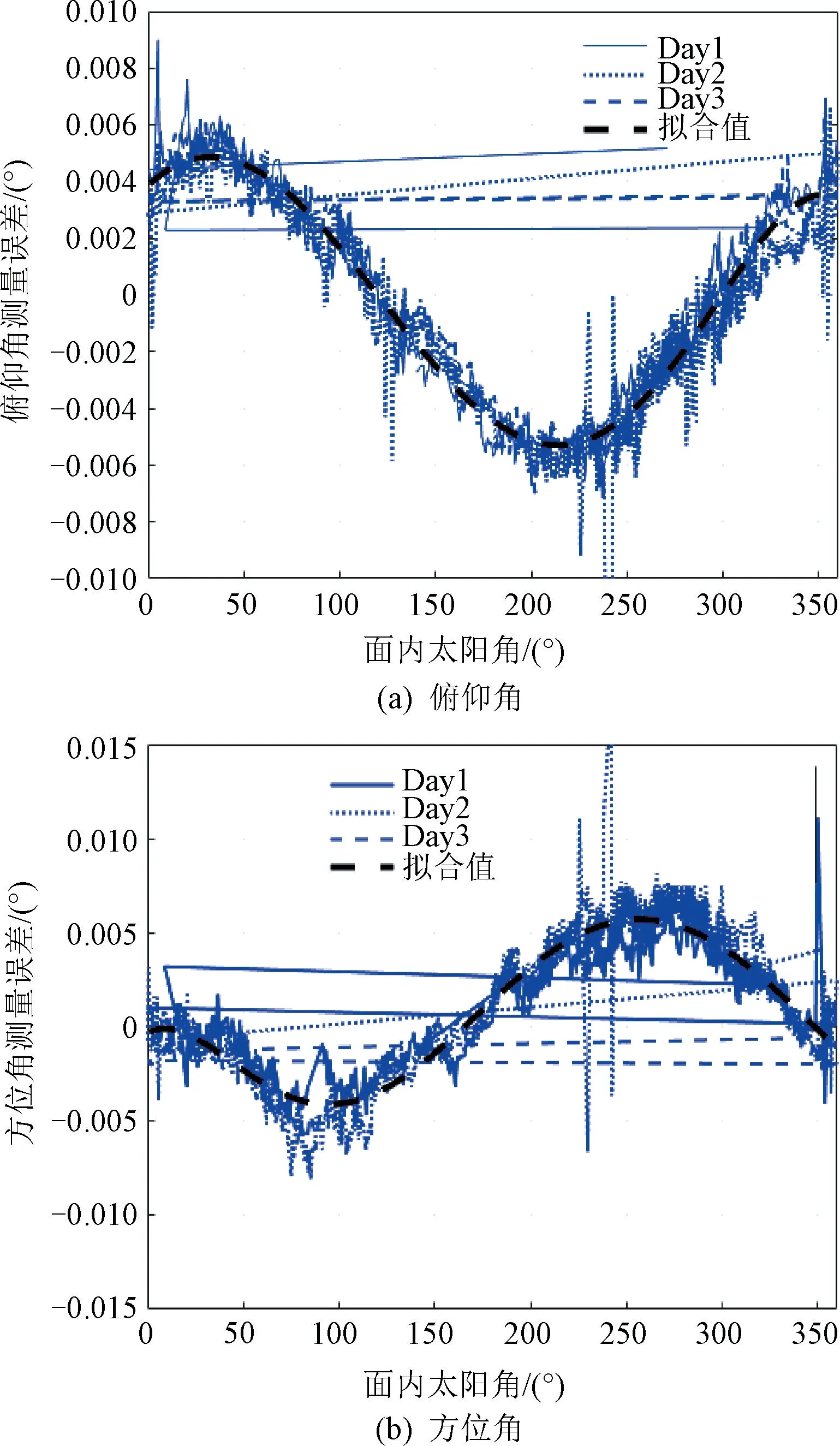
图4 低频角度误差与面内太阳角的关系曲线

由图4可知,太阳光照引起的低频角度误差中,俯仰角测量误差最大约为0.010°,方位角测量误差最大约为0.015°。

将拟合曲线与原始测量曲线进行比对,统计三倍均方差,评估拟合后的测量误差。经拟合补偿后,可以将太阳光照引起的低频角度误差控制在0.002°以内。

5 结论

本文提出了一种基于GNSS 差分定位数据的星载相对测量设备在轨标定方法。通过分析,明确影响星载相对测量设备在轨标定精度的误差项主要包括两星GNSS 差分定位误差、两星GNSS天线安装位置误差、两星姿态误差、相对测量设备和本体坐标系基准误差等。通过对上述误差项进行合理控制,可以将距离标定精度控制在5 cm 以内、将角度标定精度控制在0.002°以内。结合在轨数据开展在轨标定验证试验,验证了该方法的正确性和有效性。