基于DP-TBD的协同组网雷达方位标定误差估计与目标检测

吴熙芃,孙希平,赵泽亚,吴建新,金 雪

(1.中山大学深圳电子与通信工程学院,广东 深圳 518107;2.北京跟踪与通信技术研究所,北京 100094)

0 引言

在多雷达组网的目标检测与跟踪系统中,雷达系统标定误差的存在将直接影响组网雷达数据融合后的目标检测与跟踪。其方位角标定误差的存在将导致雷达量测数据不准确、量测结果可信度降低。因此寻找有效的雷达方位角标定方法具有重要的现实意义。

组网雷达系统方位角标定误差的估计与校正,是指组网雷达系统误差配准中的空间配准。首先对各雷达的方位角标定误差进行估计,然后再利用该估计值对雷达系统量测数据进行校正[1]。

在传统组网雷达信号处理中,估计雷达系统标定误差的方法主要分为两类[2]:第一类是将雷达量测数据与理想的目标位置数据进行比较,估计系统的标定误差;第二类是利用多部雷达对同一目标的量测数据进行处理并对比,估计系统的标定误差。第二类方法主要考虑的是固定平台雷达的空间配准[3],包括实时质量控制误差配准算法[4]、最小二乘/广义最小二乘误差配准算法[5-6]、精确极大似然配准算法[7]、基于大地坐标系的误差配准算法[8]等。上述方法均需要对各雷达的量测数据进行处理,并对目标状态和系统标定误差进行估计。这些方法在低信噪比环境下估计得到的系统标定误差较大,会影响目标的检测与跟踪。

动态规划-检测前跟踪 (dynamic programming track-before-detect,DP-TBD)是一种多帧回波数据联合处理的非相参积累方法,能够在提高雷达对微弱目标的检测性能的同时,对目标的状态信息(距离、方位角等)进行估计。相比于传统的跟踪前检测(detect before track,DBT)方法,DP-TBD 方法能够最大程度地保留目标的状态信息[9-10]。在检测前跟踪的众多实现方法中,DP-TBD 方法由于其广泛的适用性及易于实现等特点,成为学者们研究的热点[11-14]。

针对传统方位角标定误差校正方法在低信噪比环境下估计得到的系统标定误差较大的问题,本文采用多部固定平台雷达对同一目标的量测数据进行处理的方法,对各雷达的方位角标定误差进行估计。该算法利用多部雷达协同量测数据,将各雷达的坐标系统一到基准雷达(假设该雷达不存在方位角标定误差)坐标系上,利用多部雷达进行DP-TBD 处理,得到各雷达的多帧累积值函数,估计各雷达的方位角标定误差,再进行多部雷达的协同积累处理,对目标进行检测。

1 算法原理

1.1 方位角误差建模及多雷达坐标统一

假设组网雷达系统包含M部地基雷达,M部雷达对同一个目标进行观测,各雷达坐标已知,但由伺服标定引起的方位角标定误差未知。建立各雷达和目标的坐标系,雷达与目标位置及方位角标定误差如图1所示。各雷达采用数字波束形成(digital beam forming,DBF)的方式测量目标方位角。在各雷达坐标系中,雷达m的目标观测方位角和距离分别表示为θ′m和Rm,目标的真实方位角为θm,目标的方位角标定误差为Δθ′m,其中m=1,2,…,M;雷达间的基线长度为dh,其中h=1,2,…,M-1。以雷达1作为标定基准雷达,假设其方位角标定误差为0,即Δθ′1=0。误差标定后雷达m的目标观测方位角θ′m=θm+Δθ′m。

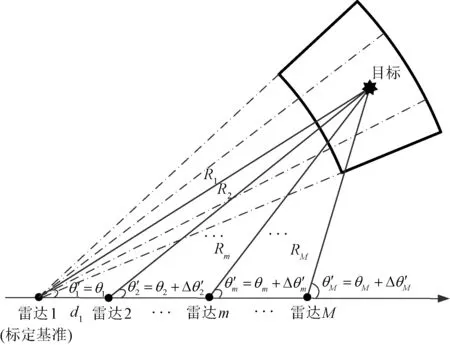
图1 雷达与目标位置及方位角标定误差示意图

各雷达接收数据处理均在距离-方位角坐标系下完成,现采用M部雷达协同的方式对Δθ′m进行估计。为了进行雷达间数据配准与融合处理,需要将各雷达的距离-方位角坐标系统一变换到雷达1 的距离-方位角坐标系中[15]。变换过程中,雷达1为融合中心雷达,其余为参与融合的雷达。根据余弦定理和正弦定理,参与融合的雷达的目标观测距离Rm和观测方位角θ′m的量测值可表示为

统一各雷达数据处理的坐标系可使用二维插值[16]方法实现。在低信噪比情况下,采用DPTBD 方法估计目标在各雷达坐标系下的方位角。统一坐标系后,对多部雷达进行协同非相参积累,对目标进行检测,同时可求得方位角标定误差。

另外需要注意的是,在本文中,各雷达是针对单目标进行检测和跟踪并估计各雷达的方位角标定误差的,如图1所示。各雷达方位角量测误差是随机的,而各雷达方位角标定误差固定但未知,此时无法区分方位角量测误差和方位角标定误差。从式(1)可以看出,组网雷达间基线长度的量测误差也将影响到统一坐标系后各雷达的方位角量测值和距离量测值。同时,由于各雷达方位角标定误差是固定的,可在方位角标定误差的估计过程中考虑距离量测误差和方位角量测误差,而不影响方位角标定误差的估计。为了突出重点,本文假设每部雷达均已知其他雷达在各自坐标系中的准确位置。

1.2 DP-TBD处理

DP-TBD 是一种多帧帧间非相参积累方法,能够最大程度地保留目标的状态信息。DP-TBD能够对目标的方位角进行估计,因此DP-TBD 方法能够直接应用到方位角标定误差的估计中,同时能对目标进行检测[9-10]。在建立的方位角误差模型和观测模型的基础上,DP-TBD 处理通过初始化、迭代递推累积和航迹回溯等步骤,得到目标的距离-方位角航迹估计序列,最后选择最接近目标真实轨迹的序列[17]。

设雷达共录取到K帧量测数据,则第k帧量测数据中,各量测单元的量测值

式中:w(k)为量测噪声幅度;A(k)为目标信号幅度。本文根据雷达方程计算各雷达接收的目标信号幅度。

DP-TBD 处理具体包括4个步骤。

步骤1:初始化。首先建立距离-方位角状态空间,状态空间离散化后的第k帧目标状态Sk=,其中rk,θk分别表示第k帧目标的距离和方位角,T为矩阵转置运算符。雷达第1次扫描(k=1)的目标状态,有

式中:I（S1）表示目标状态S1对应的阶段值;z1（S1）表示目标状态S1对应的量测值;φ(S1)表示转移到当前帧状态S1的上一帧的状态值,因当前帧为初始帧,因此将其设为0。本文采用幅度作为DP-TBD 处理的值函数。

步骤2:迭代递推累积。当2≤k≤K时,对目标状态,有

式中:I（Sk）表示目标状态Sk对应的阶段值;τ（Sk）表示第k-1帧所有的可能转移到状态Sk的离散状态的集合;zk（Sk）表示目标状态Sk对应的量测值;φ(Sk)表示转移到当前帧目标状态Sk的上一帧状态值;max(·)为求最大值函数;argmax(·)为求最大值对应的自变量的函数。

步骤3:迭代结束。假设当迭代累积到第K帧时,能量累积的最大值超过检测门限,有

式中:表示第k帧中能量累积的最大值超过检测门限的状态;VDT表示DP-TBD 的检测门限。

步骤4:航迹回溯。对每个状态,有

1.3 协同雷达方位角标定误差估计与目标检测算法

设雷达m得到的全部K帧量测数据为Zm,1:K,DP-TBD 处理后的全部K帧值函数为Im,1:K。各雷达对同一个目标进行观测,各雷达除方位角标定误差和排布位置外,所有参数均相同。

为了将各雷达量测的初始距离门对准,在探测空域已知的情况下,各雷达可在单目标所处的大致距离范围内搜索,并对单目标进行检测,确定单目标在各雷达坐标系下所处的初始距离门,最后将初始距离门对准。

由于雷达n(n=2,3,…,M)与雷达1的差异仅体现在方位角标定误差Δθ′n上,而且各雷达的位置已知。可预先设置雷达n与雷达1之间的方位角偏移网格数,组成向量Gn(l),l=1,2,…,L,L为向量长度。因此,估计Δθ′n等价于从Gn(l)中找到最优的方位角偏移网格数,并且此时已进行了准确的坐标转换。

Gn(l)的设置可采用如下方法进行。首先提取雷达1全部K帧量测数据Z1,1:K的最大值所在的方位角网格位置,组成向量θ1=;然后将雷达n的全部K帧量测数据按照1.1节方法统一到雷达1的坐标系中得到。再提取的最大值所在的方位角网格位置,组成向量最后计算雷达n与雷达1量测数据最大值所在方位角的偏移网格数向量,提取中元素的最大值。则其中:[1,+θC]L表示生成1～（+θC）之间的L个点,这些点的间距为表示向上取整;θC表示可调整的网格参数,设为整数。

为了找到最优的方位角偏移网格数,可采用搜索的方法进行。将Zn,1:K偏移Gn(l)中的一个元素值,得到,并将其统一到雷达1的坐标系中得到。对按1.2节的DP-TBD方法进行处理,得到值函数向量。最后将累加到I1,1:K上,得到第l次搜索的值函数

在遍历搜索L个点之后,将得到的值函数组成向量

通过获取最优的方位角偏移网格数,判定此时已准确进行了坐标转换。采用准则为

在搜索得到后,可得到各雷达方位角标定误差

式中:ρθ为方位角分辨率。

协同雷达方位角标定误差估计与目标检测算法流程如下。

步骤1:初始化。采集雷达n的全部K帧量测数据Zn,1:K,令l=1。

步骤2:量测数据偏移方位角网格。将雷达n的全部K帧量测数据Zn,1:K偏移Gn(l),得到。

步骤3:统一坐标系。将雷达n的全部K帧量测数据统一到雷达1的坐标系中,得到。

步骤4:DP-TBD 处理。对进行DPTBD 处理,得到值函数,并按式(7)累加到雷达1的DP-TBD 处理后的值函数上。

步骤5:循环。令l=l+1,重复步骤2 ～步骤4,直至l=L。

步骤6:提取最优的偏移方位角网格数,判定已准确进行坐标转换。在循环终止之后,得到,并按式(9)取,认为此时雷达n的值函数与雷达1重合,判定已准确进行坐标转换,再按式(10)进行各雷达方位角标定误差的计算。

经由上述处理之后,可将各雷达的值函数,其中表示雷达n的最优方位角偏移网格数,全部累加到雷达1的DP-TBD 处理后的值函数上,并结合式(5),利用该值函数对目标进行检测。协同雷达方位角标定误差估计的处理流程如图2所示。

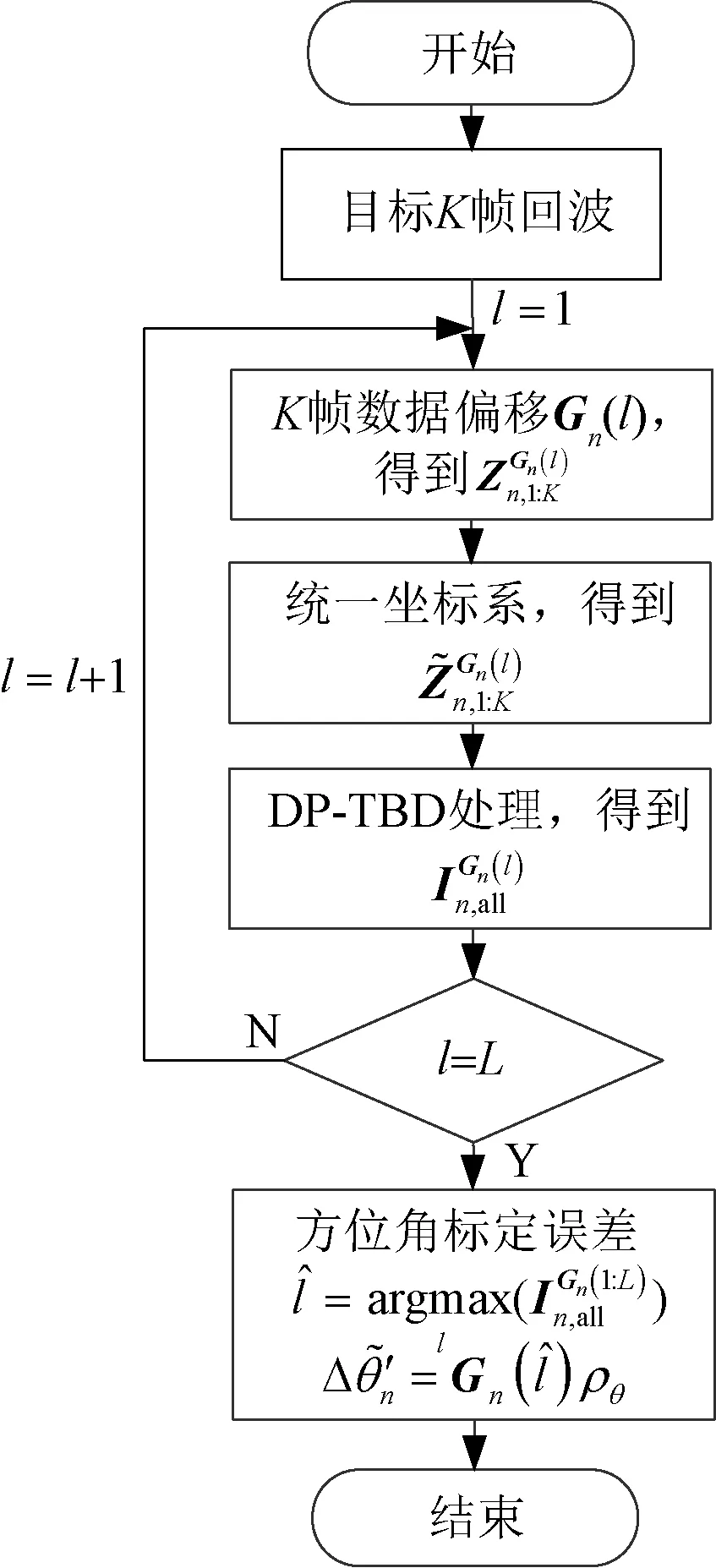
图2 协同雷达方位角标定误差估计处理流程图

2 实验验证

采用仿真数据验证算法的有效性。实验设置4部地基雷达,其中雷达1为基准雷达。考虑到工程应用中,L过大将导致搜索量的急剧增加,设置Gn(l)的向量长度L的网格数为10个,可调整参数θC的网格数为20个。

各雷达除方位角标定误差和排布位置外,其余参数均相同,各雷达波门开启时刻对应的距离均为30 km,录取数据格式为距离-方位角,采用DBF方法测角。主要仿真参数:信噪比为7 dB(高斯噪声背景下),各雷达均积累4帧数据(帧间间隔时间为1 s),过程噪声功率谱密度为0.001 m2/s4;雷达中心频率为30 GHz,带宽为100 MHz,脉宽为4μs,距离采样率为120 MHz,方位角分辨率为0.001 rad。雷达在x-y平面上排布,设定各雷达的位置坐标和方位角标定误差。雷达1的位置坐标为(0 m,0 m),方位角标定误差为0 rad;雷达2的位置坐标为(40 m,0 m),方位角标定误差为0.017 5 rad;雷达3的位置坐标为(80 m,0 m),方位角标定误差为0.034 9 rad;雷达4的位置坐标为(120 m,0 m),方位角标定误差为0.052 4 rad。设定目标的初始状态,即目标在x-y平面上的初始位置坐标x0,y0和速度分量vx,vy分别为300,300 m 和14.3,16.5 m/s。目标在x-y平面上匀速运动。雷达2～雷达4的距离-方位角坐标系将均统一到基准雷达1的距离-方位角坐标系中。

2.1 方位角标定误差估计

根据1.3节所提算法,估计雷达2～雷达4的方位角标定误差。

以雷达4为例,将雷达4的DP-TBD 处理后的值函数累加到雷达1 的DP-TBD 处理后的值函数上,对比直接进行坐标转换和方位角误差校准后进行坐标转换(已取得最优的偏移方位角网格数,第8个网格)两种情况下的方位角标定误差,如图3所示。当直接进行坐标转换时,雷达1和雷达4的目标方位角量测值之间存在偏差,如图3(a)所示。为了能够利用DP-TBD 同时对目标进行检测,采用搜索的方法继续进行坐标转换,直到找到最优的方位角偏移网格数,使雷达1和雷达4的目标观测方位角重合。在搜索到第8个网格时,雷达4找到最优的方位角偏移网格数,认为此时已准确进行坐标转换,如图3(b)所示。

图3 方位角误差校准前后坐标转换的对比图

在准确进行坐标转换之后,本文算法估计所得的方位角标定误差如表1所示。可以看到,本文算法估计所得的方位角标定误差的精度与所取的方位角偏移网格数向量Gn(l)有关。由于网格数只能取整数,最后雷达2估计所得的方位角标定误差为0.017 rad(对应网格数17,第5个网格),雷达3 估计所得的方位角标定误差为0.035 rad(对应网格数35,第7个网格),雷达4估计所得的方位角标定误差为0.050 rad(对应网格数50,第8个网格)。

表1 雷达方位角标定误差的估计

为了进一步对本文算法的估计精度进行分析,对雷达2～雷达4 在不同信噪比下各进行100次蒙特卡罗实验。设定目标在x-y平面上的初始位置坐标x0,y0和速度分量vx,vy分别为300,300 m和14.3,16.5 m/s。雷达2～雷达4的方位角标定误差估计的均方根误差(RMSE)与信噪比的关系如图4所示。可以看出,采用本文算法估计得到的各雷达方位角标定误差的RMSE随着信噪比的提升变化并不明显。

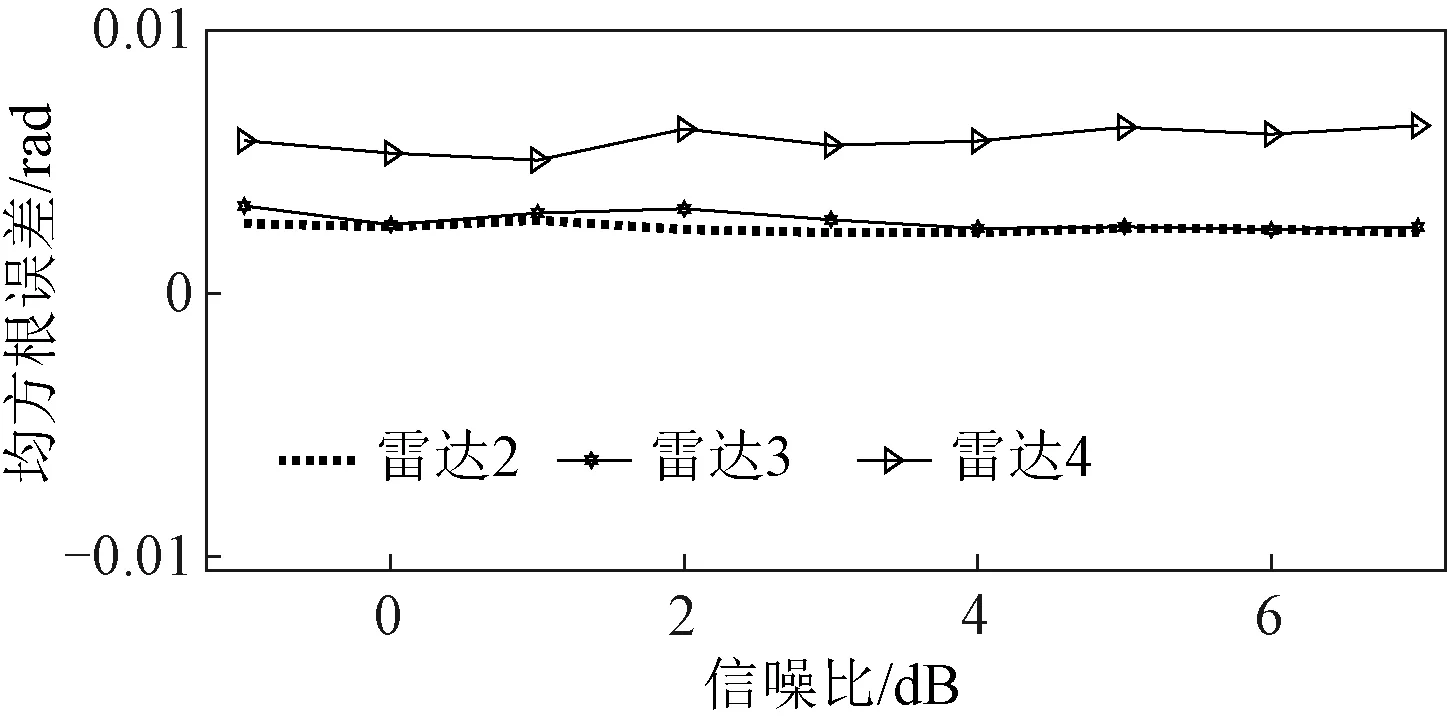
图4 雷达方位角标定误差估计的均方根误差1

在目标运动过程中,各雷达量测方位角随着雷达-目标距离的变化而变化。为了分析不同的目标运动参数对方位角标定误差估计的影响,设定目标在x-y平面上的初始位置坐标x0,y0和速度分量vx,vy分别为300,30 m,和1,1 m/s,各雷达参数及处理流程与前文相同。对雷达2～雷达4在不同信噪比下各进行100次蒙特卡罗实验。雷达2～雷达4 方位角标定误差估计的RMSE与信噪比的关系如图5所示。

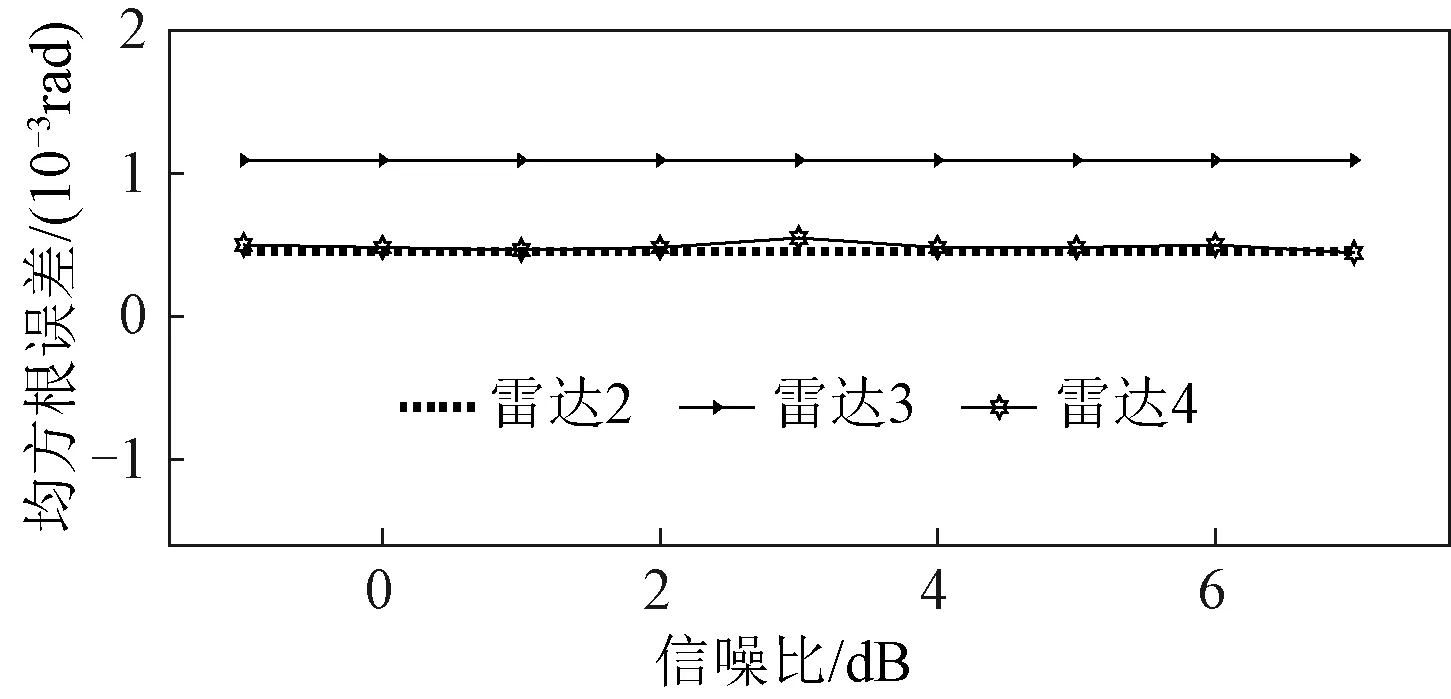
图5 雷达方位角标定误差估计的均方根误差2

从图5可以看出,在该目标运动参数下,通过本文算法估计得到的各雷达方位角标定误差的RMSE 随着信噪比的提升,变化并不明显。

对比图4和图5可以看出,在两种不同的目标运动参数下,各雷达方位角标定误差的RMSE并不相同,说明目标运动参数的改变将导致各雷达方位角标定误差RMSE的改变。

此外,在图4中,雷达4的RMSE 明显大于雷达2和雷达3的;在图5中,雷达3 的RMSE明显大于雷达2和雷达4的。这是由于受到噪声影响,各雷达依据本文方法所获取的方位角偏移网格数在每次蒙特卡罗实验中不尽相同,使得各雷达估计的方位角标定误差在每次蒙特卡罗实验中不尽相同,最终导致各雷达的方位角标定误差的RMSE不尽相同。

2.2 检测与跟踪性能分析

DP-TBD 是一种帧间非相参积累方法。其性能分析采用蒙特卡罗实验进行:在高斯白噪声背景下,当虚警概率为0.000 1时,进行20 000次蒙特卡罗实验,对1个目标进行观测。

检测性能分析共分3种情况进行。情况1:单雷达节点多帧非相参积累;情况2:不存在方位角标定误差时多雷达节点非相参积累;情况3:存在方位角标定误差时多雷达节点非相参积累。不同情况下的检测概率如图6所示。

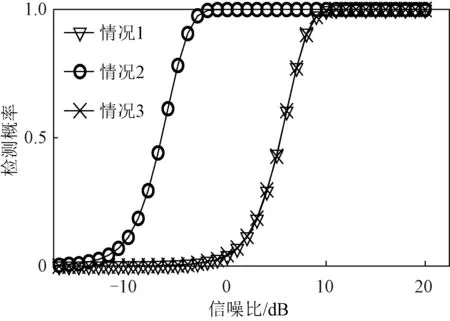
图6 不同情况下的检测概率

从图6可以看出,相比于单雷达多帧积累的情况,对校正标定误差之后的多节点组网雷达进行多帧积累,可显著提高低信噪比条件下的目标检测性能,而当存在标定误差时,组网雷达多帧积累的检测性能几乎没有改善。

跟踪性能分析在信噪比为7 dB 的条件下进行。首先对比方位角标定误差校正前各雷达恢复的目标航迹和误差校正后多雷达融合的目标航迹,如图7所示。情况1:理想目标航迹;情况2:基准雷达1恢复航迹;情况3:校正前雷达2恢复航迹;情况4:校正前雷达3恢复航迹;情况5:校正前雷达4恢复航迹;情况6:多雷达融合目标航迹。可以看到,在方位角标定误差校正前,雷达2～雷达4各自恢复的3条航迹均与理想目标航迹存在差距,主要是在方位角上存在差距;在方位角标定误差校正后,将各雷达航迹融合,与理想目标航迹进行对比,可以看到融合后的航迹与理想目标航迹具有良好的一致性,尤其是在方位角上并没有明显的差距。

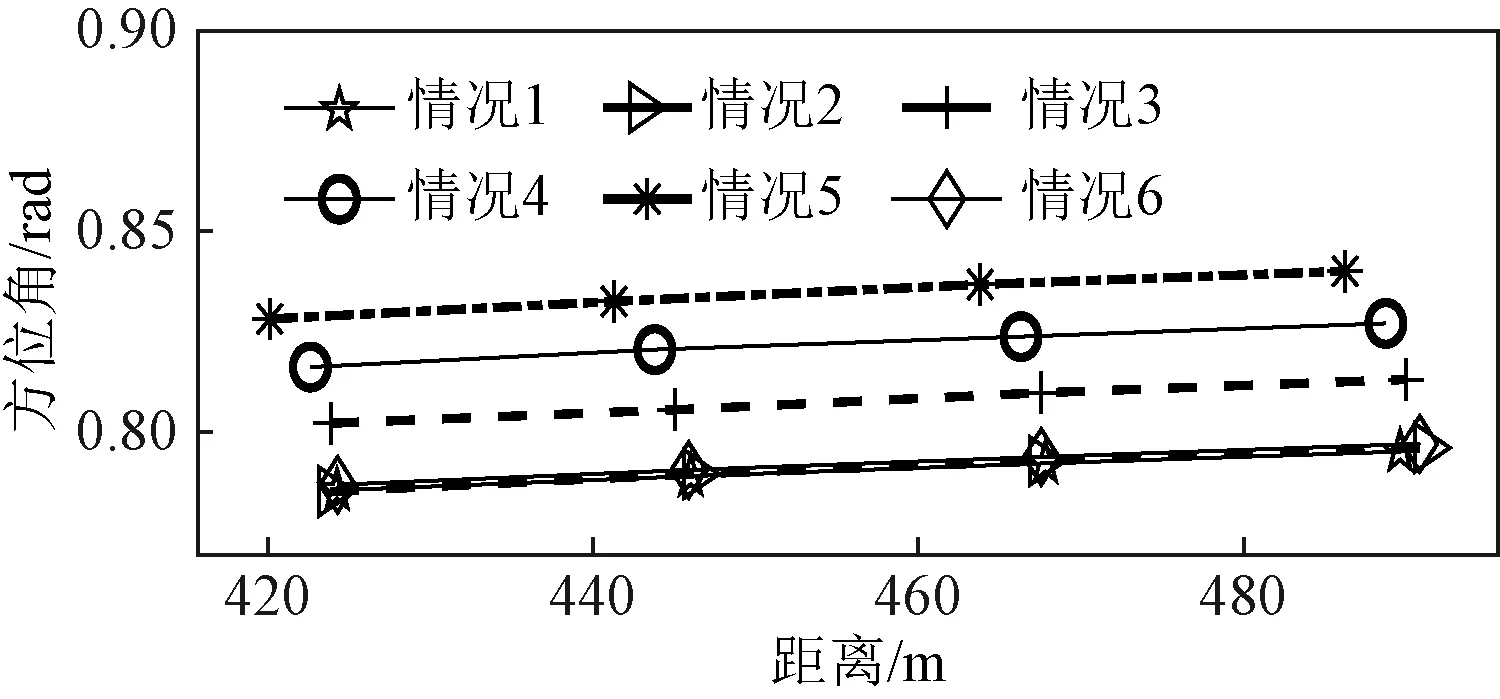
图7 误差校正前后恢复的航迹

图7中的目标跟踪误差(绝对误差)均值,如表2所示。可以看到,多雷达融合后的目标跟踪误差均值比雷达2～雷达4校正前的目标跟踪误差均值小。

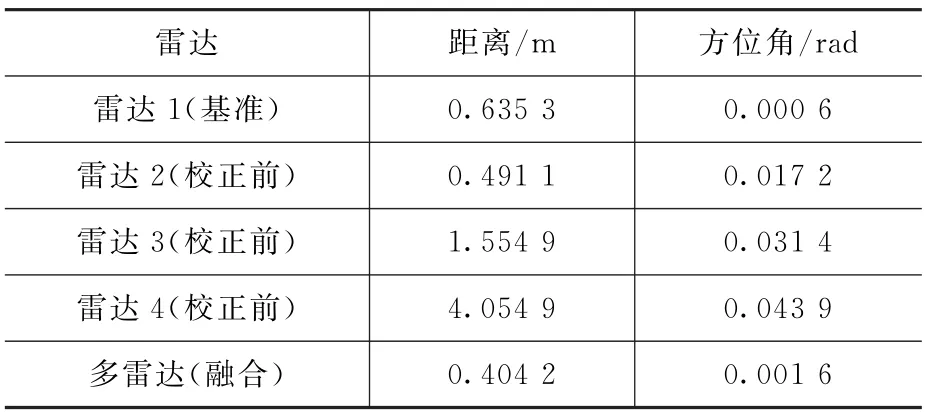
表2 目标跟踪误差均值

3 结论

本文提出了一种基于DP-TBD 的协同组网雷达方位角标定误差估计方法。该算法将DPTBD 和多雷达协同处理结合起来,能直接利用量测数据估计组网雷达的方位角标定误差,并进行多雷达协同积累,实现目标检测,可显著提高低信噪比条件下的目标检测性能。仿真结果验证了算法的有效性。