一种基于模糊参数自适应调整的温度控制系统设计方法
赵明翰,李乃星,曹培培,郑秋实,李俊杰
(上海无线电设备研究所,上海 201109)
0 引言
随着农业生产技术的快速发展,温室农作物的高效率种植对温室温度的控制精度以及控制效率提出了更高的要求。温室是指通过对设施内的环境进行高精度控制,实现种植作物周年连续生产的高效农业系统。温室栽培[1-2]是利用计算机和传感系统对植物生长环境进行自动控制,使设施内的植物生长发育不受或很少受自然条件制约的省力型生产方式。
温室的立体栽培形式可使栽培面积提高几倍甚至几十倍,并可实现周年不间断栽培。随着我国国民经济的发展和人民生活质量的提升,我国温室将迎来最佳发展机遇期,市场前景十分广阔。目前我国温室总面积已经超过300万公顷,位居世界第一。其中,具备智能环境控制能力的联栋温室因其效率高、周期短、耗能少和不易受气候影响等优点而成为现代智慧农业发展的方向。但目前我国温室总面积中该类温室占比不到3%。究其原因,在于连栋温室可控设备多、控制复杂,属高投入高产出的先进温室,且大多使用国外的环境控制设备,投产及使用维护成本居高不下,这严重抑制了我国高科技温室的推广发展。因此,提升国产温控设备的温度控制效率与精度,优化现有国产温室控制系统的设计方案具有重要意义。
相比于一些发达国家,我国对温室的研究起步相对较晚。近年来,随着传感器、自动化、物联网技术的发展,国家在智慧农业领域的政策支持和财政投入力度越来越大,对温室的研究也进入了高速发展阶段。文献[3]提出了一种基于多传感器并行控制多个控温设备的系统。该系统可提升温室的网络化和分布式管理效率,但需要挂载多个回路,控制过程较为复杂。文献[4-5]提出了基于自动控制器的动态温度控制回路处理方案。该方案可有效提升温度控制精度,但最终温度收敛速度较慢,温控压缩机需要频繁启停,影响压缩机的使用寿命以及温度控制效率。文献[6]提出了基于加热炉的温度控制方式,可实现温室加热功能,但该温控方式精度较低,无法满足较高精度的温控要求。
本文提出一种温度控制方案,采用模糊比例-积分-微分(proportion integration differentiation,PID)自适应控制算法,提升温度控制效率,缩短温度收敛时间,避免温控压缩机频繁启停。本方案不增加额外的探测及温控设备,通过优化回路控制实现温控精度以及温控效率提升。
1 系统建模
在空调系统的工作过程中,高压的液态制冷剂通过膨胀阀进入蒸发器,吸热汽化形成低压气体,再经过压缩机压缩变为高压气体,然后通过冷凝器冷凝变回高压液体,如此循环,实现热量的搬运。温度的变化过程一般可以分为两个阶段:制冷剂热循环和空间温度交换循环[7]。
对于制冷剂的热循环过程,由于涉及到复杂的相变过程和热传递过程,因而难以建立精确的数学模型。一般认为以空调压缩机为输入,制冷剂热量转换为输出的传递函数为一阶惯性环节[8]。同时,由于制冷剂的热交换过程需要一定时间,因此需要在传递函数中增加时滞环节。制冷剂的热转换传递函数框图如图1所示,其中K为比例系数,T为时间常数,τ为滞后时间。

图1 制冷剂热转换传递函数框图
结合实际物理环节进行测试,得到系统参数K=5,T=1,τ=5 s。最终得到以空调压缩机为输入、制冷剂热量转换为输出的传递函数
对于制冷剂热量转换过程,首先对不考虑时滞环节的传递函数进行建模分析,再在得到的数学模型上增加时滞环节,最终完成模型的建立。
在建立不包含时滞环节的模型时,需要进行如下假设:a)忽略风扇对空气的做功;b)忽略空间内空气的热传递,认为空间内的空气温度一致;c)忽略湿度变化对温度的影响。在满足这些假设条件的前提下,空间中的能量平衡方程可写为
式中:Qr表示空间内空气具有的热量;Qf表示空调系统向空间内空气传递的热量;Qw表示被控空间以外向空间传递的热量;Qd表示空间内部物体向空间内空气传递的热量,包括设备工作产生的热量和人员活动产生的热量。
假设整个过程中空气密度ρ、定压比热容Cp和空间体积Vr不变,则Qr随时间t的变化可以通过室温tr随时间t的变化来表示,即
根据式(2),将Qw和Qd对空间空气温度的影响整合为总扰动d,为了方便研究,将总扰动d设定为常数扰动。此时,可以得到室温变化量Δtr的增量形式的微分方程
式中:Tr为室温惯性系数;Kr为扰动引发的温度变化量到室温变化量的传递系数;Δtd为扰动引发的温度变化量。
可以看出,此时的传递函数具有一阶惯性环节的形式,相关参数通过对已有的实际温室进行多次测量取平均得到,对应的传递函数
联合式(1)和式(5),得到系统传递函数
同时,由于在实际的系统运行过程中,选定工作模式后,热量只能进行单向传递,因此需要在控制输出端增加一个下限为零的饱和环节[9],最终得到的系统原理框图如图2所示。在图2的基础上可以进行后续控制器的进一步设计。
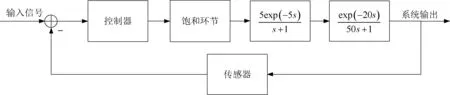
图2 系统原理框图
2 模糊控制器设计
模糊控制是以模糊集合理论、模糊语言变量和模糊逻辑推理为基础的一种新型智能控制方法[10-11]。其本质是依靠专家经验,模拟人的行为来进行决策和控制[12]。模糊控制的基本过程是:首先通过模糊化接口,利用符合实际情况的模糊规则,对输入信号进行模糊化处理[13];然后将已经模糊化处理的输入信号与事先设计好的由专家经验构成的规则库进行对应;最后再利用解模糊化接口将模糊变量转换成精确的输出量来进行控制[14]。模糊控制的基本原理如图3所示。
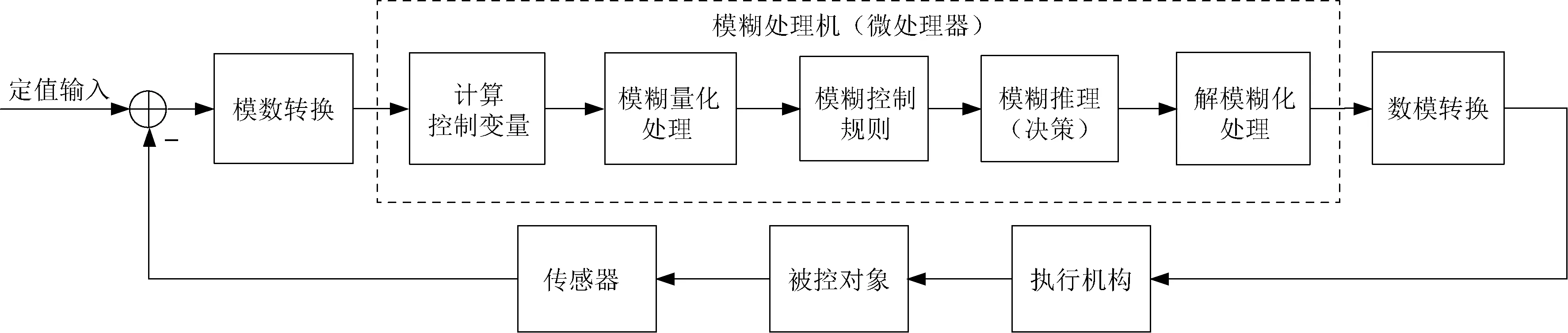
图3 模糊控制的基本原理框图
对于本文中的研究对象,使用二维模糊控制器,选取偏差量e和偏差量的一阶微分e·(在实际系统中为偏差量的一阶差分Δe)作为模糊控制器的输入,采用“If A and B,then C”的模糊控制规则[15]。将模糊控制器的输出比例参数Kp、积分参数Ki和微分参数Kd作为PID控制器的输入。得到的模糊PID 控制器原理框图如图4所示。
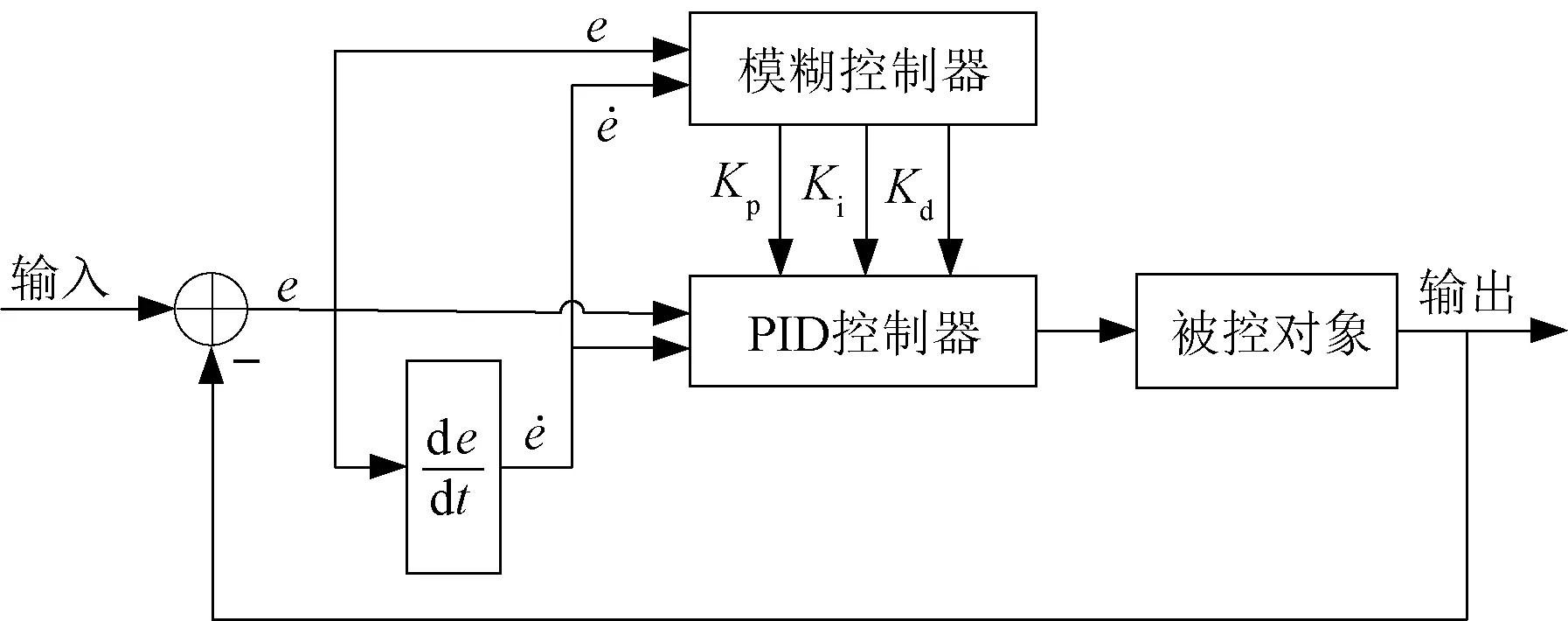
图4 模糊PID 控制器原理框图
定义e和模糊子集为{LN,MN,SN ZERO,SP,MP,LP} ,其分别表示控制偏差e和偏差量一阶微分在模糊集合中处于{负大,负中,负小,零,正小,正中,正大}子集中。模糊控制规则见表1~表3。
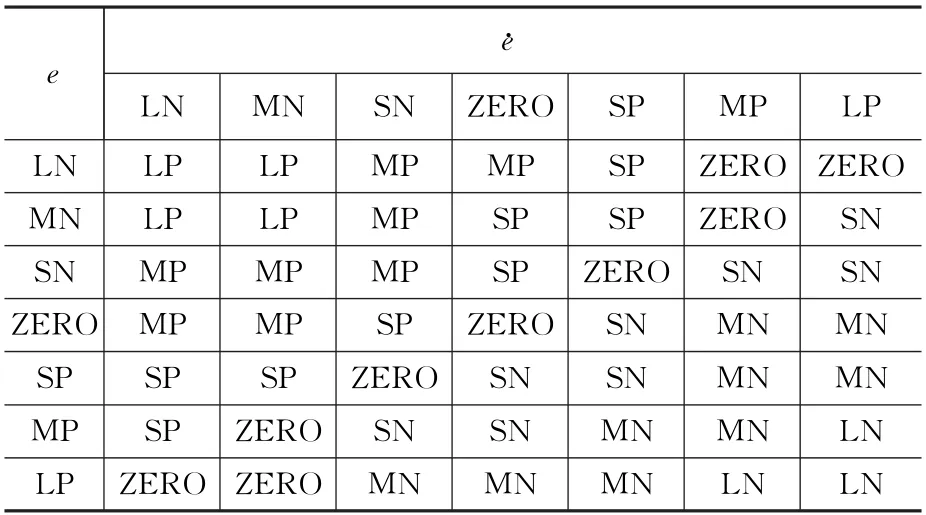
表1 Kp 模糊控制规则表
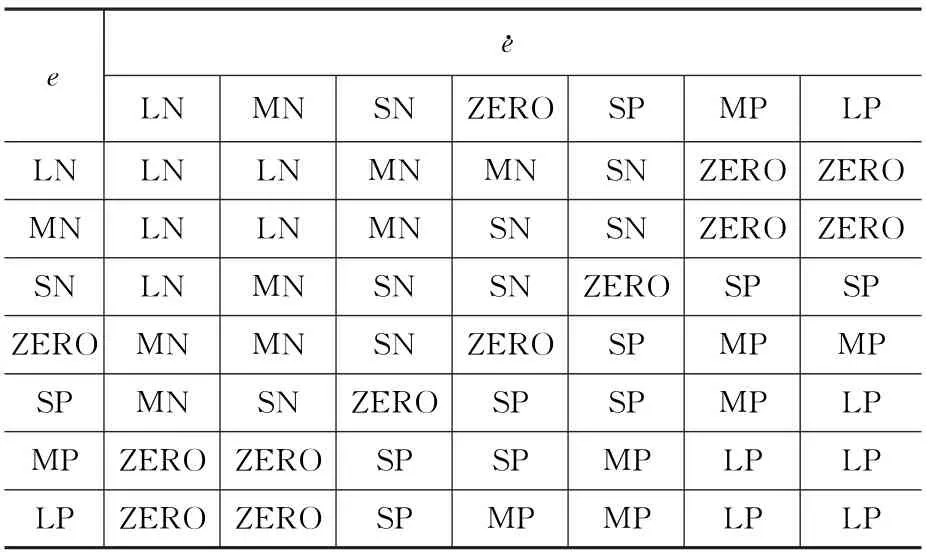
表2 Ki 模糊控制规则表
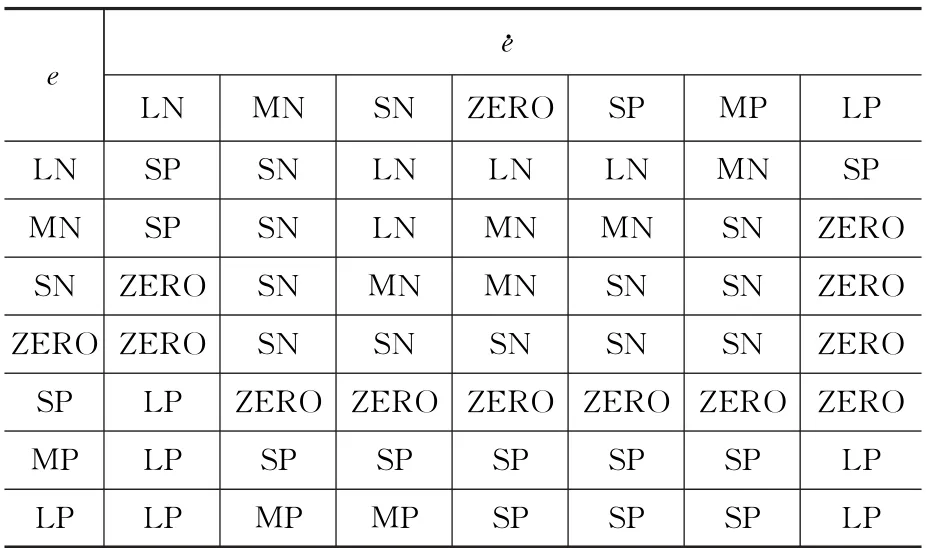
表3 Kd 参数模糊控制规则表
通过模糊控制器得到PID 控制器的参数Kp,Ki,Kd[16],再将参数带入传统的PID 控制器,得到模糊PID 控制器。对应的算法公式为
式中:u(k)为k时刻的控制指令;e(k)为k时刻的偏差量;T为控制周期。
3 仿真验证
根据得到的数学模型对温室温度控制系统模型进行仿真分析。设输入温度为3 ℃的阶跃信号,扰动为常值扰动。
首先进行单位负反馈控制,得到的输出温度曲线如图5所示。
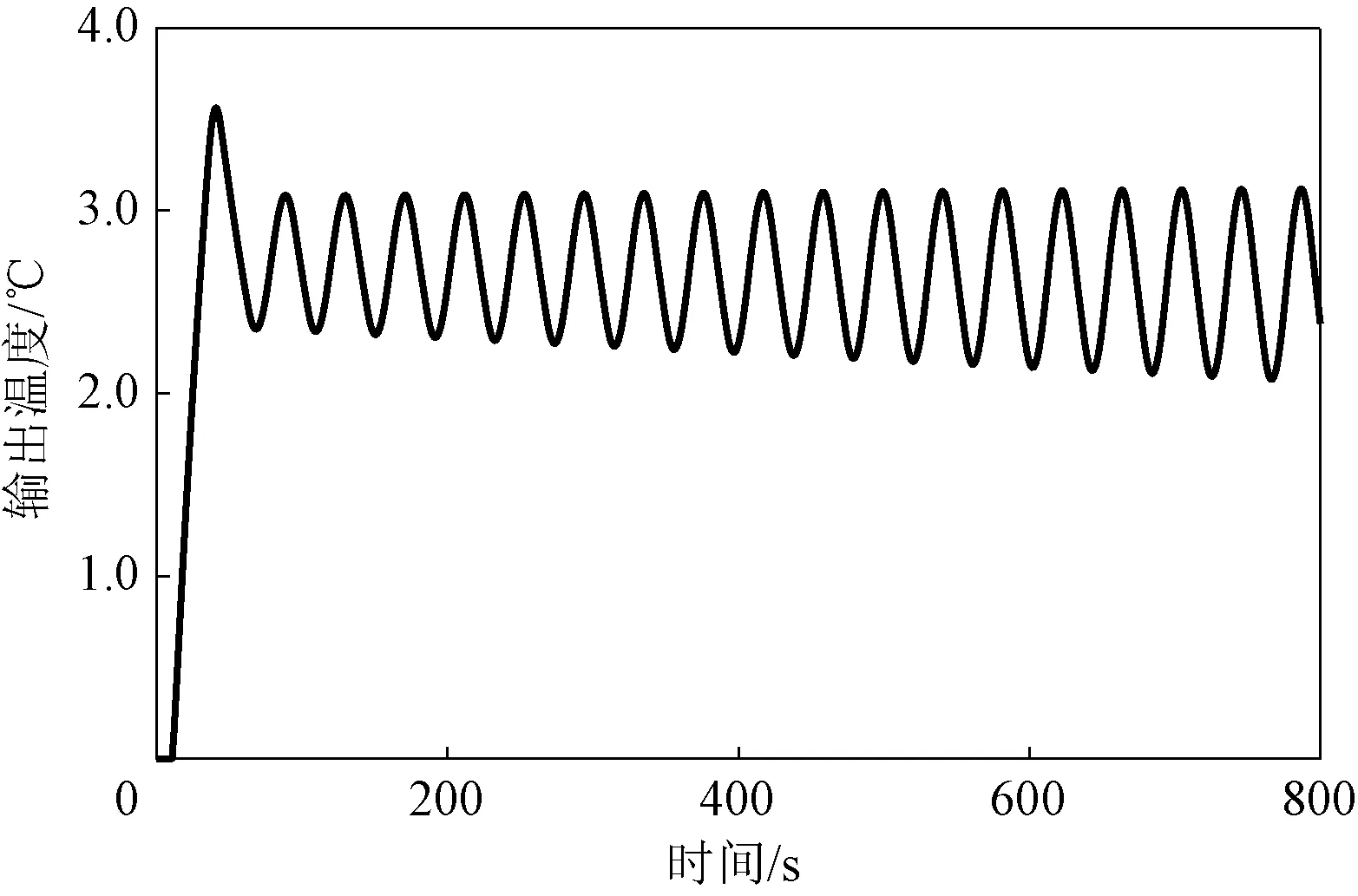
图5 单位负反馈控制下温度变化曲线
由图5可以看出,由于系统中存在时滞环节,系统存在明显的超调。同时,由于系统中存在常值扰动信号和非线性饱和环节,实际的输出温度并不能稳定在3℃,而是在持续振荡,甚至存在发散的趋势。
采用传统PID 控制,得到的输出温度曲线如图6所示。
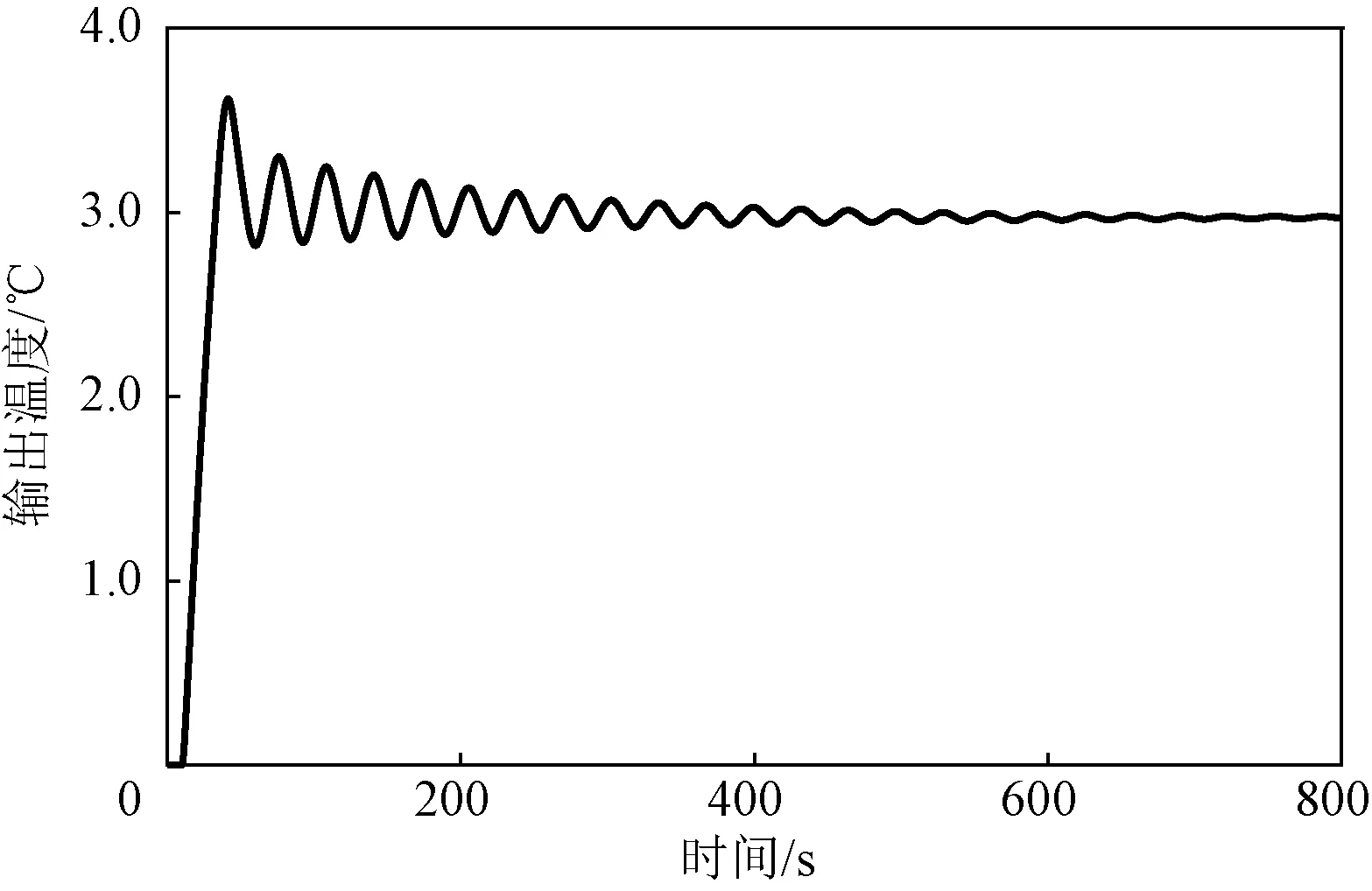
图6 传统PID 控制下温度变化曲线
由图6可以看出,相较于单位负反馈控制,使用传统PID 控制能够保证系统收敛,但收敛速度较慢,存在明显的振荡现象。温控系统的控制精度为0.1℃,调节时间为600 s。对于仿真结果中表现出的振荡现象,在实际的物理系统中将反映为压缩机的频繁启停,这会对压缩机的使用寿命产生不良影响。同时,温度的反复振荡也会使作物生长受到影响。因此,需要尽量减少振荡次数,以优化压缩机工作状态,延长压缩机的使用寿命并提高作物生长效率。
采用模糊PID 控制时,得到的系统输出温度曲线如图7所示。
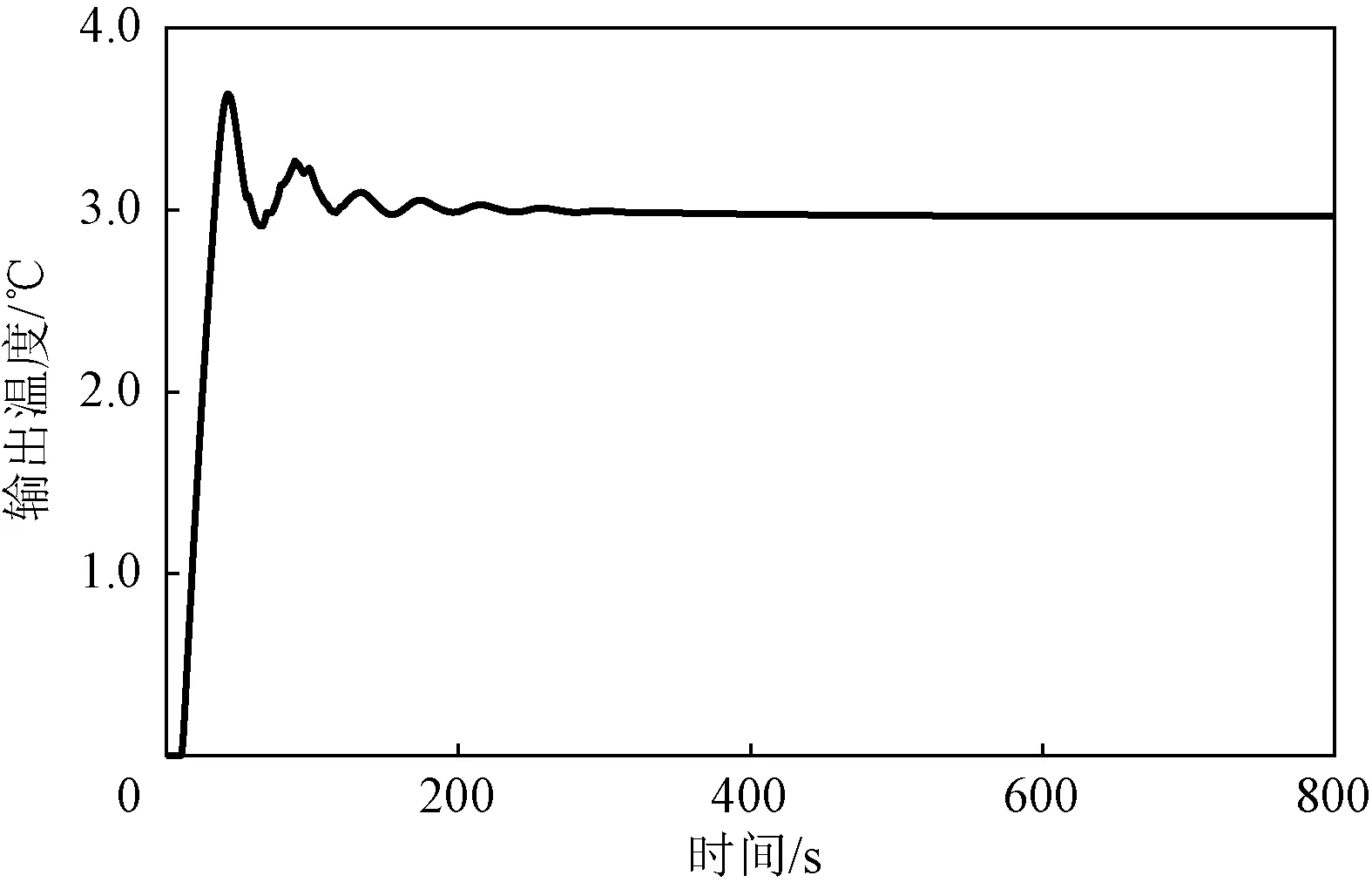
图7 模糊PID 控制下温度变化曲线
从图7 的结果来看,使用模糊PID 控制后,系统的收敛速度明显加快,振荡次数明显减少,性能得到了明显改善。温控系统稳态控制精度小于0.05℃,温度调节时间小于300 s。从作物生长效率和压缩机寿命的角度来看,更少的温度振荡次数意味着更高的作物生长效率,同时,更少的振荡次数会明显减少压缩机的启停次数,对于提高压缩机寿命有着积极意义。
4 结束语
本文针对温室温度控制系统设计了一种基于模糊PID 控制的自适应控制器,并结合具体的温室模型进行了设计及仿真验证。仿真结果表明,相比于其他温室温度控制方法,本文提出的基于模糊PID 的自适应控制器具有更高的温度控制精度以及更短的温度调节时间,可以有效提升温控设备的控制效率。同时,本文提出的优化算法不需要额外增加探测及控制设备,具有较强的工程实用性。

