基于位姿分离的机械臂解析求逆优化算法

隋 涛, 孔刘君, 姜 昊, 蒋 强

(沈阳理工大学 自动化与电气工程学院, 沈阳 110159)

机械臂作为机器人的重要执行机构,可以模拟人们的手臂去完成各项工作[1],其自主操作能力和执行大量任务的能力已经引起了研究人员和工业界的广泛关注.机械臂在执行各项任务时,通常需要解决逆向运动学问题,这是实现机械臂运动控制[2]、轨迹规划[3]和避障[4]的前提.

机械臂的逆向运动学问题常被称作是“运动学的珠穆朗玛峰问题”[5],其本质是完成从机械臂工作空间到关节空间的映射[6],这种映射关系具有非线性和多耦合性.多年来国内外许多优秀学者对机械臂的逆向运动学问题开展研究.蔡改贫等[7]提出的APSO-LM-BP神经网络算法解决了传统神经网络求取逆解时容易陷入局部极小值的缺陷.KHAN等[8]提出的双粒子群算法分别对位置和姿态问题进行优化,改善了收敛性能.TOZ[9]提出的基于混沌的涡旋搜索算法有效降低了最大迭代次数.上述几种智能算法虽然在不同维度上进行了改进,但在稳定性、控制精度等方面仍面临巨大挑战,而解析法恰巧避免了上述问题.韩硕[10]与程浩田[11]将几何法与矩阵逆乘相结合,求解精度较高,但算法较为抽象繁琐.李海[12]减少了矩阵逆乘的次数,但仍停留在对4维矩阵的处理层面,运算量较大.

针对上述问题,本文以ROKAE XB7型机械臂为研究对象,提出一种结合位姿分离思想的解析求逆优化算法.该算法将4维矩阵运算分别降低为1维和3维矩阵运算,在保证其计算精度的同时,能够有效避免以往解析法的复杂求解过程,提高运算效率.通过蒙特卡洛法获取仿真数据点,并在Matlab仿真环境下验证改进算法的稳定性与有效性.

1 机械臂正向运动学

1.1 正向运动学建模

本文所研究的ROKAE XB7型机械臂具有6个转动关节,前3个关节决定机械臂所能到达的位置,后3个关节决定其到达指定位置时的姿态.根据机械臂的结构特征及外形尺寸,采用改进型D-H方法[13]建立如图1所示的连杆坐标系.

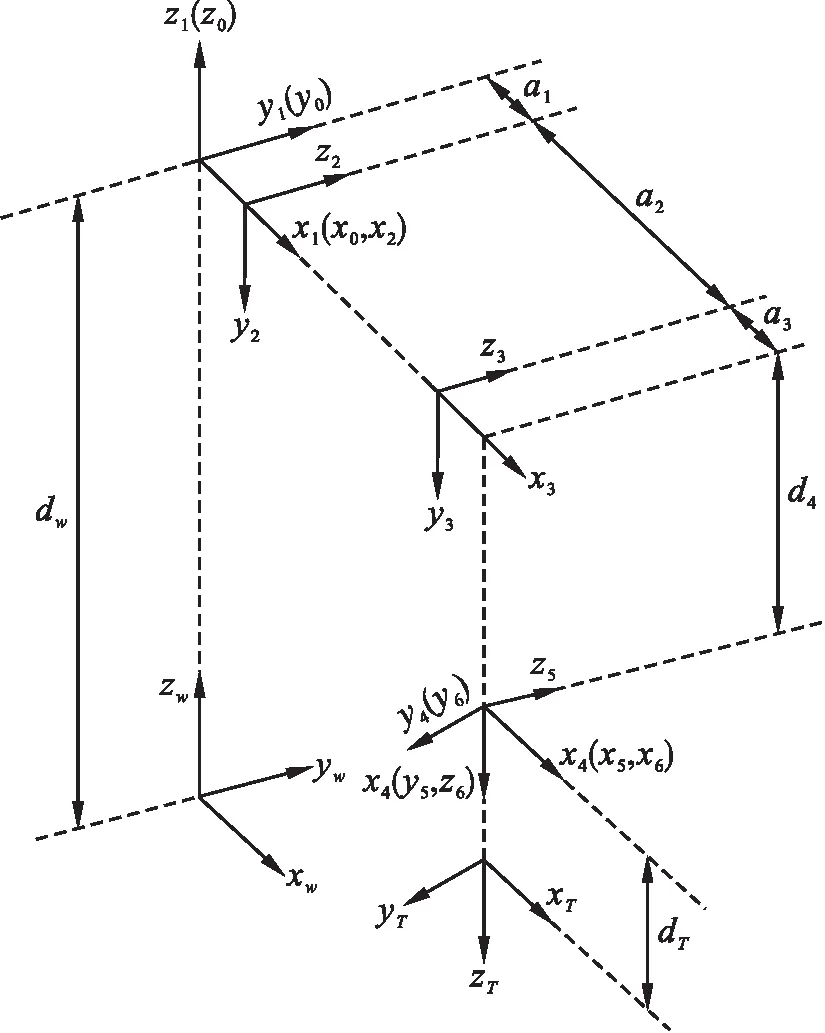
图1 机械臂连杆坐标系Fig.1 Coordinate system of manipulator link

改进型D-H参数法建系得到的相邻两连杆坐标系变换矩阵[14]为

(1)

式中:αi-1为连杆扭转角;ai-1为连杆长度;di为连杆偏距;θi为关节角.机械臂的D-H参数如表1所示.

表1 机械臂D-H参数Tab.1 D-H parameters of manipulator

1.2 正向运动学求解

机械臂的正向运动学求解是指已知机械臂各关节变量,求取末端位姿的过程[15].根据表1中的D-H参数和式(1),得到机械臂末端坐标系相对于基坐标系的变换矩阵,即

(2)

(3)

式中:R3×3为旋转矩阵,表示机械臂的末端姿态;P3×1为位置矢量,表示机械臂的末端位置;s23=sin(θ2+θ3);c23=cos(θ2+θ3);si=sinθi;ci=cosθi.

2 机械臂逆向运动学

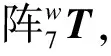
(4)

2.1 位置逆解的求取

根据位置矢量P3×1求取前3个关节角.由px/py可以求解θ1,即

(5)

对px和pz进行变换整理可得

(a3s23+d4c23+a2s2)2

(6)

经化简及三角恒等变换可得

θ3=atan 2(a3,d4)-

(7)

(8)

对pz进行变换整理可得

pz=-s2(a3c3+a2-d4s3)+c2(-a3s3-d4c3)

(9)

对上式进行三角恒等变换可得

θ2=atan 2(K3,K2)-

(10)

(11)

2.2 姿态逆解的求取

根据旋转矩阵R3×3求取后3个关节角.由旋转矩阵性质可知

(12)

(13)

令式(13)两边矩阵的元素(2,3)相等,则

(14)

由式(15)可求得θ5,即

θ5=atan 2(s5,c5)

(15)

令式(13)两边矩阵的元素(1,3)和(3,3)相等,则

(16)

由式(16)可求得θ4,即

θ4=atan 2(r13s1-r23c1,r13c1c23+

r23s1c23-r33s23)

(17)

令式(13)两边矩阵的元素(2,1)和(2,2)相等,则

(18)

由式(18)可求得θ6,即

θ6=atan 2(r12c1s23+r22s1s23+r32c23,

-r11c1s23-r21s1s23-r31c23)

(19)

2.3 最优解的选取

通过式(5)～(9)可求得机械臂的8组逆解,然而,在实际应用中往往仅需1组最优逆解即可,故可采取以下步骤选取最优解:

1) 舍去不满足各关节转角范围的解.

2) 基于节省能耗与最佳柔顺性原则,采用性能函数来确定最优解,函数值越小,说明性能越好.性能函数定义为

(20)

式中:ωi为第i关节对应的权重(i越大,ωi越小);Δθi为第i关节逆解的角度与当前角度的差值.

3 机械臂工作空间分析

机械臂的工作空间是指其末端所能到达的范围.对工作空间进行分析,可为后续仿真验证部分提供大量实验数据.在Matlab中通过编程方式完成对机械臂工作空间的求解(蒙特卡洛法)[18],具体流程如图2所示.

图2 机械臂工作空间求解流程Fig.2 Flow chart for solution of manipulator workspace

取N=30 000,得到如图3所示的机械臂工作空间点云图.由图3可知,ROKAE XB7型机械臂工作性能良好,其工作范围是一个半径约为0.707 m的球体.由于受到机体构造的约束,机械臂的可达空间存在一个较小缺口,因此,在选取实验数据时应避免选择缺口处的不可达工作点.

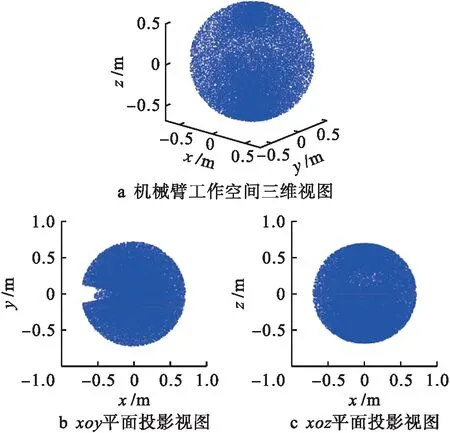
图3 机械臂工作空间点云图Fig.3 Point cloud maps of manipulator workspace

4 机械臂仿真分析

采用CPU为Intel Core(TM) i7-6700HQ 2.60GHZ的计算机,利用Matlab仿真软件对机械臂的运动学模型及正逆运动学算法进行验证分析.

4.1 正向运动学仿真验证

在机械臂的关节空间内,随意选择一组关节角[π/3,π/5,-π/4,π/6,π/4,π/5],其3D仿真模型如图4所示,其中qi为关节变量.

图4 机械臂模型Fig.4 Model of manipulator

基于机械臂正向运动学方程设定上述选定的关节角,得到机械臂末端的位姿矩阵,即

(21)

为了验证正解算法的正确性,调用Robotics Toolbox中的fkine函数进行验证,结果表明求解结果与式(21)一致,验证了正解算法及所建模型的正确性.

4.2 逆解算法单点测试

按照式(21)设定机械臂末端期望位姿,将其代入基于本文逆解算法的Matlab程序中,得到如表2所示的8组逆解.

表2 机械臂8组逆解Tab.2 Eight inverse solutions of manipulator

由表2可知,第2组逆解结果与初始设定的关节角度一致.为了验证其余各组逆解的准确性,将余下7组逆解依次代入正向运动学方程.经验证得知,各组计算结果均与式(21)吻合(忽略仿真计算导致的浮点误差).在机械臂的工作空间内随机选取多个工作点进行逆解算法验证后发现,该算法具有较高控制精度与良好稳定性.

4.3 逆解算法连续轨迹测试

在机械臂工作空间内,任取起始位置Tstart和终止位置Tend,并已知起始位置所对应的关节角θstart.三个设定条件具体数据为

(22)

(23)

θstart=[0,π/4,-π/18,π/5,-π/4,π/4]

(24)

利用Matlab Robotics工具箱中的ctraj函数生成10个路径点,采用本文提出的算法得到如图5所示的连续轨迹逆解拟合曲线.由图5可知,连续轨迹逆解曲线光滑,并未出现较大跳变,证实了所提逆解算法及最优解选取原则应用于后续机械臂轨迹规划、运动控制等方面研究的可行性.

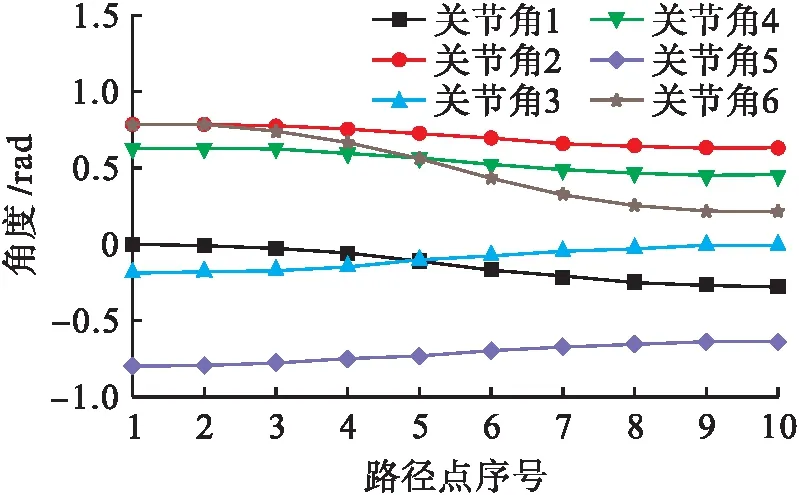
图5 连续轨迹逆解拟合曲线Fig.5 Fitting curves of continuous trajectory inverse solutions

4.4 逆解算法对比分析

基于李海[12]提出的解析求逆优化算法思路,对本文搭建的机械臂模型进行逆向运动学算法设计.在设计算法的过程中发现该算法虽然较传统解析法减少了矩阵逆乘的次数,但仍需对4维矩阵进行高达3次的逆乘运算,公式推导过程繁琐复杂.而本文提出的逆解算法充分利用机械臂的结构特点及位姿矩阵特性,可以间接实现矩阵降维运算,降低了逆解算法的设计难度.同时,本文提出的逆解算法有效避免了其他算法[10-11]设计过程的抽象、不直观的问题.

为了进一步证实算法的优越性,在机械臂的工作空间内,任取10个不同位姿,利用Matlab软件采用本文所提算法与李海[12]所提算法对各位姿分别进行50次求逆运算,将两个算法的各位姿平均求解时间进行对比,结果如图6所示.本文所提算法与李海[12]所提算法对10个位姿的平均求解时间分别为0.197 ms、0.298 ms,本文算法求解效率提高了33.89%,表明本文所提算法减少了求解过程的程序运行时间,具有更好的实时性.

图6 不同逆解算法的求解时间对比Fig.6 Comparison of solution time of different inverse solution algorithms

5 结 论

采用改进型D-H参数法搭建ROKAE XB7型机械臂运动学模型.结合位姿分离思想提出一种解析求逆优化算法.利用蒙特卡洛法对机械臂的工作空间进行分析,获取了机械臂可达工作点信息范围.通过Matlab仿真软件验证了所提算法的稳定性与优越性.与现阶段解析求逆优化算法相比,本文算法克服了求解复杂繁琐、计算成本高等诸多弊端.本文算法的提出不仅可为机械臂后续相关研究奠定基础,同时可为多关节机械臂逆向运动学求解提供新思路.