可变磁路式永磁悬浮系统线性自抗扰控制分析
李 强, 张鹏飞, 赵 川, 徐方超, 金俊杰, 孙 凤
(沈阳工业大学 机械工程学院, 沈阳 110870)
磁悬浮技术是利用磁力平衡物体重力,实现无接触稳定悬浮的技术.如今所使用的磁悬浮主要以电磁悬浮技术为主,在磁悬浮轴承[1]、磁悬浮列车[2]、磁悬浮电机[3]和磁力悬架[4]等多个领域内广泛使用.超导悬浮技术[5]主要应用于超导磁悬浮列车,分为低温超导磁悬浮列车(液氦)和高温超导磁悬浮列车(液氮),我国研发的时速600 km/h磁悬浮列车就属于高温超导磁悬浮列车[6].与永磁悬浮技术相比,电磁悬浮技术具有需要以电力不断供给磁力以及较大能耗的缺点.我国稀土资源储备丰富,对发展永磁悬浮技术具有诸多便利.上海大学袁昆鹏等[7]研究设计了满足长寿命和高转速工作要求的无刷直流电机永磁轴承,并进行了力学特性分析;刘建文等[8]提出了一种轴流式人工心脏泵,其中叶轮转子采用两个永磁轴承提供被动支撑.
本文实现物体稳定悬浮的方法为电机驱动径向磁化圆柱形永磁体旋转,改变通过导磁体与悬浮物的磁通量,实现悬浮力大小的控制,使其平衡悬浮物重力进而实现悬浮[9].可变磁路式的永磁悬浮系统具有高阶性、强非线性和时滞性的特点,实现稳定悬浮控制较为困难.目前已有较多控制方法应用在该磁悬浮系统中,如PID控制器[10]、鲁棒控制[11]等,其中最常用的为PID控制器,PID控制结构虽然简单明确,但在磁悬浮系统的抗干扰能力方面有较大的局限性.自抗扰控制也应用在一些磁悬浮系统中,但主要用于电磁悬浮中,而在永磁悬浮中大多都仅限于仿真阶段,实验成果较少.
自抗扰控制(ADRC)[12]是由韩京清研究员提出的,其核心思想是在尽可能不受精确的数学模型影响下,使用扩张状态观测器将整个系统包括外扰和内扰在内的集成扰动观测出来,通过设计非线性控制律将所产生的误差加以补偿,从而达到快速收敛的目的,具有较强的抗扰动能力.线性自抗扰控制方法具有不依赖精确的数学模型,抗干扰能力强,参数较少,易于整定的特点,因此,本文设计的可变磁路式永磁悬浮系统采用线性自抗扰控制方法,证明了线性自抗扰控制方法具有广泛的通用性.
1 永磁悬浮系统结构及工作原理
1.1 磁悬浮系统结构
可变磁路式永磁悬浮系统的原理样机如图1所示.

图1 永磁悬浮系统的原理样机Fig.1 Principle prototype of permanent magnetic levitation system
该永磁悬浮系统的组成结构主要包括圆柱状永磁体、“F”型导磁体、传感器、悬浮物和调节千分尺.其中,圆柱状永磁体的充磁方式为径向充磁,与伺服电机通过联轴器连接;“F”型导磁体处于永磁体两侧,对称分布;传感器位于悬浮物体下方,用于测量悬浮物体与导磁体之间的气隙;调节千分尺用于调节悬浮物、传感器、永磁铁和导磁体的相对位置.
1.2 磁悬浮系统工作原理
图2为可变磁路原理图.径向磁化的永磁铁与伺服电机相连接,由伺服电机进行驱动,当永磁铁的转角为0°时,永磁体的主磁通经两侧“F”型导磁体全部由N极返回S极,悬浮物无主磁通经过,不产生磁力.当永磁铁转过θ°时,此时除了经过两侧“F”型导磁体由N极返回S极主磁通外,还有部分主磁通将从N极出发,先后经过右侧“F”型导磁体、悬浮物及左侧“F”型导磁体返回S极,并产生一定磁力.

图2 可变磁路原理图Fig.2 Principle diagram of variable flux path
2 数学模型建立
永磁悬浮系统模型受力如图3所示.图3中,d0为系统平衡时的气隙,Δd为悬浮物位移变化量,Δd=d-d0,向下为正方向,θ为永磁体转角,θ0为永磁体在平衡位置时的转角,Δθ为角度变化量,Δθ=θ-θ0,顺时针方向为正.

图3 永磁悬浮系统模型图Fig.3 Model diagram of permanent magnetic levitation system
经实验数据可得,悬浮物所受磁力均随着旋转角度呈周期性变化,采用等效磁路法可求解得出磁力解析关系和永磁体转动过程中受非线性转矩作用的关系.推导可变磁路式永磁悬浮系统动力学方程为
(1)
(2)
式中:J为电机与永磁体的转动惯量;kt为伺服电机转矩系数;i为伺服电机输入电流;m为悬浮物的质量;c1为永磁体在回转方向上的阻尼系数;c2为悬浮物运动阻尼系数;f为外扰力;F为永磁体对悬浮物的吸引力;τ为永磁体受到的转矩.
将式(1)、(2)在平衡位置进行线性化处理,可得到最终线性化模型为
(3)
(4)
式中:kτ为磁转矩系数;Δdτ为磁转矩漏磁补偿系数;km为悬浮力系数;Δdf为导磁体弧形漏磁补偿系数.
3 串级LADRC控制器设计
3.1 控制方案设计
永磁悬浮系统采用PID控制虽然可以实现收敛,并最终达到稳定,但系统响应速度较慢,抗干扰能力较差.自抗扰控制可以在被控对象不是非常准确的情况下实现控制,并具有较好的抗干扰能力.线性自抗扰控制具有结构简单、参数整定方便、扰动跟踪性能几乎不随扰动幅度发生变化等特点,因此,本文选用线性自抗扰控制.
由可变磁路式永磁悬浮系统控制原理可知,如果只采用气隙闭环控制,角度变化缓慢,控制信号无法及时控制永磁体转角,加之系统本身由电流信号转换到永磁铁转角具有一定的滞后性.因此,采用双闭环控制,内环为角度闭环采用PD控制器,外环为气隙闭环采用LADRC控制器.角度环的控制目标是控制盘状永磁体的旋转角度,气隙环的控制目标是控制悬浮物的位置,使悬浮物稳定.串级线性自抗扰控制示意图如图4所示.

图4 永磁悬浮LADRC控制系统原理图Fig.4 Principle diagram of permanent magnetic levitation LADRC control system
3.2 LADRC控制器设计
根据磁悬浮系统的数学模型及控制方案可知,角度环和气隙环都是二阶数学模型,本文主要分析二阶LADRC控制器的算法.
LADRC结构主要包括线性扩张状态观测器(LESO)和线性状态误差反馈控制器(LSEF).LADRC控制器结构图如图5所示.通过设计扩张状态观测器,以实时预估对象模型中的全部扰动为目标,设计一个PD状态反馈控制器,消除扰动对系统输出的影响.LADRC将自抗扰控制策略简化为整定控制器带宽ωc和观测器带宽ω0两个量,从而实现对扰动的实时观测和补偿.

图5 二阶LADRC控制器结构图Fig.5 Structure diagram of second-order LADRC controller
3.2.1 LESO设计
二阶系统LESO方程可表示为
(5)

(6)
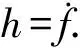
建立线性扩张状态观测器方程为
(7)
选取合适的观测器增益β1、β2、β3,LESO能实现对系统中各变量的实时跟踪.
采用带宽法将观测器特征方程的极点放在同一位置-ω0处,即
λ(s)=s3+β1s2+β2s+β3=(s+ω0)3
(8)
可得
3.2.2 LSEF设计
LADRC采用PD控制器作为线性状态误差反馈控制器,其表达式为
u0=kp(r-z1)-kdz2
(9)

(10)
同样用带宽配置,经过参数化可得
3.3 改进LADRC控制器设计
针对LADRC观测器受系统带宽限制所带来的观测及抗扰能力不足的问题,本文以提高线性自抗扰控制器的抗扰能力为目标,对传统的LADRC结构框架进行改进,设计LESO控制器时将模型中已知部分代入LESO中进行辅助设计,从而提高控制效果.其中线性状态误差反馈控制器的设计保持不变.
对本文磁悬浮系统动力学建模可以得到式(5)中a1、a2,而ω、b未知,则该式可以改写为
(11)

(12)

对应的扩张状态观测器方程式为
(13)
式中:z为观测器的状态变量,z→x;L为观测器误差反馈增益矩阵.重写观测器方程式为
(14)
式中:uc=[u,y]T为组合输入;yc为输出.
观测器增益矩阵为
L=[β1,β2,β3]T
(15)
采用带宽法配置,最终可得
由上述分析可知,采用模型辅助的LESO改进LADRC控制器结构如图6所示.
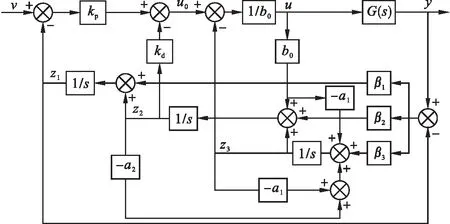
图6 辅助模型二阶LADRC控制器结构图Fig.6 Structure diagram of auxiliary model second-order LADRC controller
4 改进LADRC参数整定
根据LADRC的工作原理,二阶LADRC控制器共有b0、ω0、ωc3个参数需要整定.通过频域分析可知,LADRC控制器参数整定时,带宽的选取对系统的稳定性能和动态特性都有较大影响.图7~9分别为通过频域分析法分析b0、ω0、ωc3个参数取不同值时对系统性能的影响.

图7 ω0变化的闭环伯德图Fig.7 Bode diagrams of closed-loop with variation of ω0
从图7中可以看出,当ω0逐渐增加时,闭环系统的带宽变化不大,对系统动态特性影响较小.从图8中可以看出,当ωc逐渐增加时,闭环系统的带宽增大,系统调节时间减小.从图9中可以看出,当b0逐渐增加时,闭环系统的带宽减小,系统调节时间增大.综合考虑系统的稳定性和动态特性,本文外环LADRC控制器参数整定为b0=13、ω0=150、ωc=80.

图8 ωc变化的闭环伯德图Fig.8 Bode diagrams of closed-loop with variation of ωc

图9 b0变化的闭环伯德图Fig.9 Bode diagrams of closed-loop with variation of b0
5 仿真结果与分析
对该系统进行阶跃外扰仿真和抵抗外扰力仿真,并将传统LADRC控制、改进LADRC控制、PID控制分别作为串级控制的外环,PD控制作为内环的3种控制方式进行对比分析.
5.1 位移阶跃仿真分析
3种控制器阶跃外扰仿真结果如图10所示.系统在进入稳定后的1 s时,加入幅值为0.1 mm,方向为气隙变大方向的阶跃外扰信号.采用PID控制时超调量为45.57%,稳定时间约为0.8 s;采用LADRC控制时,超调量为23.53%,稳定时间约为0.6 s;采用改进LADRC控制时,几乎没有超调量,稳定时间约为0.3 s.

图10 阶跃外扰仿真结果Fig.10 Step disturbance simulation results
5.2 抵抗外扰力仿真分析
3种控制方法抗外扰力仿真结果如图11所示.系统在进入稳定后的1 s时,加入幅值为0.5 N,方向为使气隙变大方向的外扰力.采用PID控制时气隙最大变化量为0.21 mm,稳定时间约为0.86 s;采用LADRC控制时,气隙最大变化量为0.18 mm,稳定时间约为0.68 s;采用改进LADRC控制时,气隙最大变化量为0.12 mm,稳定时间约为0.41 s.

图11 抗外扰力仿真结果Fig.11 Anti-disturbance simulation results
对比分析可得3种控制方法中控制效果最好的为改进LADRC控制,系统响应速度较快,超调量小,响应曲线较为平滑.
6 结 论
本文通过上述分析可得如下结论:
1) 本文对单自由度可变磁路式永磁悬浮系统进行控制研究,提出了改进LADRC控制方法,以弥补传统PID控制动态性能差、控制精度较低的缺点和传统LADRC受带宽影响导致抗扰能力不足的问题.
2) 本文系统采用了双闭环控制,角度环采用PD控制器,气隙环采用LADRC控制器.通过对比分析改进LADRC控制、传统LADRC控制和经典PID控制的阶跃外扰与抗外力仿真结果,表明采用改进LADRC控制器对可变磁路式永磁悬浮系统控制时,超调量较小,调节时间较短,较传统LADRC和传统PID控制其动态性能有所提高.

