浮沉子不可逆现象的探究*
苗燕茹 姚关心 许新胜
(安徽师范大学物理与电子信息学院 安徽 芜湖 241002)
1 引言
2021年全国大学生物理学术竞赛中提出了这样一个探究性的问题:将一个简单的浮沉子放在一个装满水的长竖直管中,管中压力的增加会迫使浮沉子下沉,当达到一定深度时,即使压力变回初始值,沉浮子也不会返回初始位置.对浮沉子这种不可逆现象的研究工作也有不少报道[1-2],但都主要集中在浮沉子的制作方法和不同运动状态的描述上,而对浮沉子的不可逆现象的物理本质研究相对较少.本文将对不同状态浮沉子进行动力学分析,给出浮沉子不可逆现象的合理解释.
2 浮沉子的动力学理论分析
2.1 浮沉子模型
一个上端开有小孔、内部注有液体并留存一部分气体空间、可以实现上浮和下沉的物体被称为浮沉子,其示意图如图1所示.
2.2 浮沉子运动特点
浮沉子初始漂浮于水面上,对密封装置施加外力后,装置液面上方空气体积减小,压力增大,浮沉子向下运动,当浮沉子下沉至一定深度且处于无速度状态时撤去所施加的压力,此时会出现一种最常见的现象——浮沉子回复至初始位置,称为可逆转的浮沉子. 但一定条件下,会出现撤压后不会回复的情况,称为不可逆转的浮沉子.
大量实验表明,在液面以下存在一个可以使浮沉子可逆与不可逆状态发生改变的临界位置[3],且在此处浮沉子速度为零(浮沉子加速度方向在此处实现了从撤压向上到撤压向下的转变).针对浮沉子运动过程中的特点,建立相应的浮沉子物理模型,其示意图如图2所示.
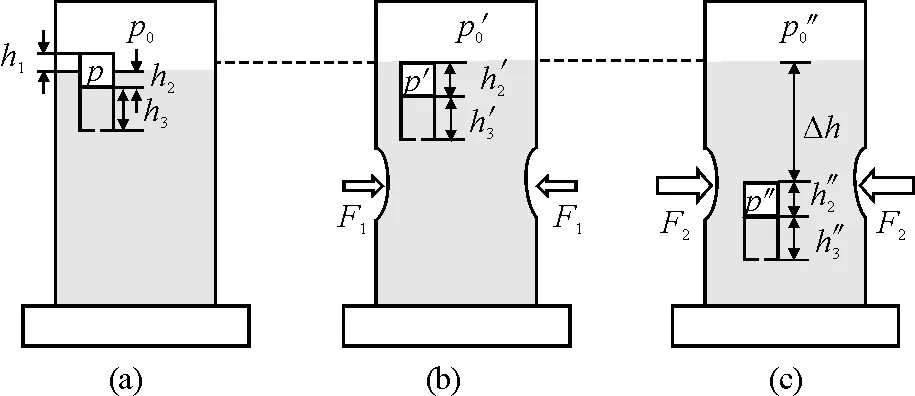
(a)浮沉子静止漂浮;(b)对装置施力F1,浮沉子静止悬浮于液体中且无下沉深度;(c)对装置施力F2,浮沉子下沉Δh且处于临界位置图2 浮沉子的3种平衡状态示意图
2.3 浮沉子动力学过程理论分析
采用不同规格且顶端开有直径为1~2 mm小孔的玻璃瓶制作浮沉子(利用玻璃瓶,所展示的相关可逆或不可逆现象更为明显且对原理分析无影响).
由阿基米德原理(忽略浮沉子的外壳体积)和力的平衡
mg=ρgh2S
(1)
mg=ρgh′2S
(2)
mg=ρgh″2S
(3)
式(1)、(2)、(3)中,m为浮沉子质量,S为浮沉子截面积,ρ为液体密度,g为重力加速度,h2为图2(a)中位于液面以下的气柱长度,h′2为图2(b)中浮沉子内气柱长度,h″2为图2(c)中浮沉子内气柱长度.联立式(2)、(3)有
h′2=h″2p′=p″
(4)
式(4)中,p′、p″分别为图2(b)和图2(c)中浮沉子内上方气体压强.
对3种状态下的浮沉子进行受力分析,根据力的平衡有
mg+p0S=pS
(5)
mg+p′0S=p′S
(6)
mg+p″0S+ρgΔhS=p″S
(7)
式(5)、(6)、(7)中,p0、p′0、p″0分别为图2(a)~图2(c)中外部容器上方气体的压强,p为图2(a)中浮沉子内上方气体压强,Δh为图2(c)中浮沉子下沉深度.
对图2(b)和图2(c)状态下的浮沉子底端进行分析有[3]
p′+ρgh′3=p′0+ρg(h′2+h′3)
(8)
p″+ρgh″3=p″0+ρg(h″3+h″2+Δh)
(9)
式(8)中h′2、h′3分别为图2(b)中浮沉子内气柱长度、水柱长度,式(9)中h″2、h″3分别为图2(c)中浮沉子内气柱长度、水柱长度.
化简式(8)、(9)可得
p′=p′0+ρgh′2
(10)
p″=p″0+ρg(h″2+Δh)
(11)
若把空气的压缩过程看成等温压缩过程[4],则有
p(h2+h1)S=p′h′2S
进一步可求得
(12)
结合式(4)、(11)、(12),浮沉子的临界位置的表达式可写为
(13)
为了更加直观地看出浮沉子自身参数对Δh的影响,联立式(1)、式(13)可写成
(14)
若要让图2(b)中的浮沉子下沉,需要对装置进行施压,使外部容器上方气体压强增大.此状态下必有
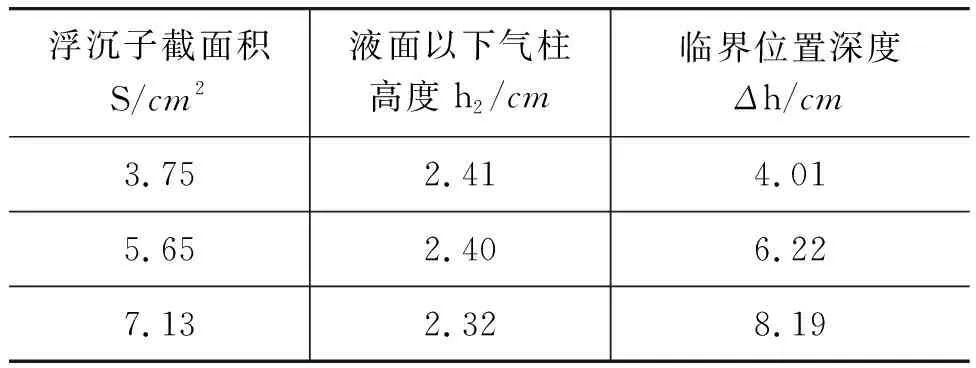
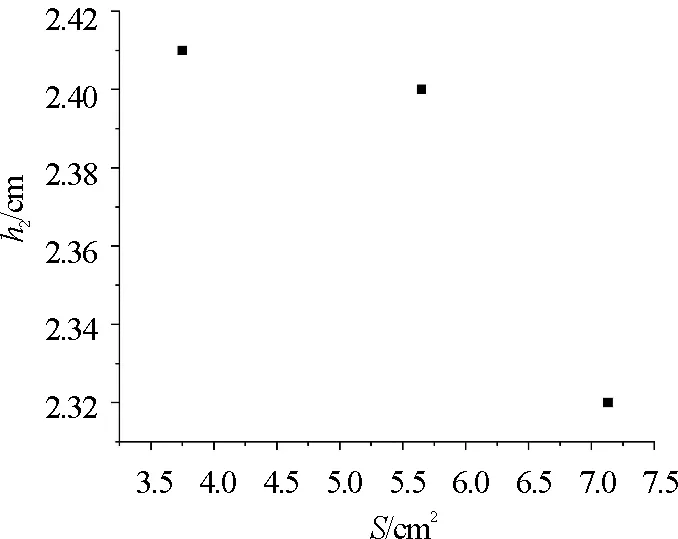
p′0 联立式(10)、(11),其中Δh>0,得 p′ 显而易见,此式与式(4)相矛盾. 为了满足式(4)成立,联立式(10)、(11),得到 p′0=p″0+ρgΔh (15) 即在浮沉子下沉Δh后,立即减小外部容器内气压p″0,并使之小于p′0,才能使得等式成立. 但仅在外界大气压作用下,外部压强最低只能降回到图2(a)中的情况,即与大气压相等.所以这里p″0的取值范围为[p0,p′0),在此情况下,控制浮沉子下沉深度Δh与p″0之间的变化,才能满足式(4).即浮沉子下沉后只有减压才能使之在水下达到受力平衡位置(即临界位置),从而产生不可逆现象. 但是,若减压过度或下降高度与减压不匹配,将会导致 p′0≠p″0+ρgΔh 例如减压过度,会使得p″ h′2>h″2 则式(3)变为 mg>ρgh″2 代入式(7)发现使浮沉子下沉的力大于使之上升的力,不可逆现象由此发生. 采用制作材料规格相同、顶端开有直径为1~2 mm小孔的玻璃瓶进行浮沉子制作,浮沉子和外部容器带有刻度,其最小分度值为1 mm. 选取质量、截面积、长度都相同的浮沉子,使用配重铜丝增改其质量,并确保在改变浮沉子整体质量的同时不改变其排水体积(即把所加配重铜丝放至浮沉子内部),测量出每次实验相对应的h2(液面以下气柱高度)和Δh(临界位置深度),如表1所示. 表1 浮沉子质量m对h2和Δh的影响 选取横截面积相同的浮沉子,使用配重铜丝维持其质量不变,测量出每次实验相对应的h2(液面以下气柱长度)和Δh(临界位置深度),如表2所示. 表2 浮沉子截面积S对h2和Δh的影响 利用相关软件绘制不同实验参数下关于h2和Δh的散点图,如图3~图6所示. 图3 质量m与气柱高度h2之间的关系 图4 质量m与临界位置深度Δh之间的关系 图5 截面积S与气柱高度h2之间的关系 图6 截面积S与临界位置深度Δh之间的关系 由图3~图6可知,浮沉子自身参数会对临界位置产生影响,具体表现如下:随着浮沉子质量的增加,其液面以下气柱高度增加,临界位置深度逐渐减小,而截面积的增加所带来的影响与上述相反. 实验中还观察到:浮沉子若要发生不可逆,则其初始位置就必须与液面齐平或与液面极接近.由式(13)可得,当h1为零时,由于h1所在的这一项含有p0,对于浮沉子临界位置深度Δh而言变小了很大一部分,所以在浮沉子完全浸没时,相比于有露出的情况下,临界位置深度Δh更小. 通过上述理论分析和实验数据结果表明: (1)浮沉子下沉后只有减压才能使之在水下达到受力平衡位置.产生不可逆现象的根本原因为过度放压. (2)浮沉子的自身参数(质量m、截面积S)是通过影响液面以下气柱高度h2进而影响临界位置的深度.3 浮沉子运动规律实验验证
3.1 实验方案及数据记录




3.2 实验结果分析

4 结论

