磁控条件下激波冲击三角形气柱过程的数值研究∗
董国丹 张焕好 林震亚 秦建华 陈志华 郭则庆 沙莎
1)(南京理工大学,瞬态物理国家重点实验室,南京 210094)
2)(北京电子工程总体研究所,北京 100854)
本文基于磁流体动力学方程组,在保证磁场散度为零的条件下,采用CTU+CT(corner transport upwind+constrained transport)算法,对有无磁场控制下激波与重质或轻质三角形气柱相互作用过程进行数值研究.结果表明:无论有无磁场,两气柱在激波冲击下均具有完全不同的波系结构和射流现象.其中,入射激波与重气柱发生常规折射,形成介质射流,而与轻气柱作用则发生非常规折射,形成反相空气射流.无磁场时,气柱在激波冲击下,产生Richtmyer-Meshkov和Kelvin-Helmholtz不稳定性,界面出现次级涡序列,重气柱上下角卷起形成主涡对,轻气柱空气射流穿过下游界面后形成偶极子涡.施加横向磁场后,次级涡序列、主涡对以及偶极子涡均消失.进一步研究表明,在磁场作用下,洛伦兹力将不稳定性诱导产生的涡量向界面两侧的Alfvén波上输运,减少界面涡量沉积,抑制界面卷起失稳.最终,涡量沿界面两侧形成相互远离的涡层,界面不稳定性得到控制.此外,定量分析表明磁场能加快两气柱上游界面的运动,抑制下游界面的运动,且对轻气柱的控制效果更好.
1 引 言
激波与不同流体分界面相互作用的过程中,诱导界面微弱扰动从线性发展为非线性,此现象广泛存在于兵器发射、航空、航天、天体力学、地质物理、核能以及化工等领域,其蕴含了湍流转捩以及激波与涡相互作用等复杂的流体物理现象[1−3].Richtmyer基于Taylor线性理论,对激波冲击界面、诱导界面失稳的现象进行研究,提出了预测界面增长的脉冲加速模型,该预测随后被Meshkov的激波管实验所证实.因此激波冲击气体分界面,进而诱导界面失稳的现象被称为Richtmyer-Meshkov(R-M)不稳定性[4,5].
自R-M不稳定性提出以来,人们对其进行了大量的研究.Rudinger和Somers[6]实验研究了激波分别冲击小尺度H2,He与SF6气柱的宏观运动过程,提出了一个预测界面涡量和速度的简单理论模型.随后,Haas和Sturtevant[7]对激波与球形和柱形He,R22气柱进行研究,他们结合光学知识进行分析,发现激波经过重质R22气柱后,在气柱内部汇聚,而后经过轻质He气柱后发散,但对于激波与两种介质气柱相互作用过程中具体波系发展没有给出详细的说明.Layes等[8,9]采用高速纹影图像技术对激波冲击轻质He、重质Kr以及等质N2气柱进行了实验研究,发现在轻气柱上游顶点会形成反向空气射流,重气柱下游界面则会形成介质射流,而等质N2气柱界面形状无明显变化,但是对于两种完全不同射流形成机理没有给出明确的解释.Ranjan等[10,11]分析激波与不同马赫数He球形气泡作用过程中的复杂波系、界面发展和涡量产生等复杂物理现象,发现作用过程中会产生不同的折射现象,这与激波入射角和介质有关.
早期的研究多局限于球形和柱形界面,但是激波与界面作用过程中的折射现象与入射角密切相关.近年来,人们开始对不同几何外形气柱的波系结构和界面发展进行深入研究.Zhai等[12]实验研究了激波与正方形、长方形,三角形、菱形轻质(He)气柱作用过程中复杂波系结构以及界面扰动发展过程,发现激波与轻气柱发生非常规折射,并出现非常规折射之间的转换.Luo等[13]对激波与正方形、长方形、三角形、菱形重质(SF6)气柱进行研究,发现不同几何外形气柱具有不同的波系结构和射流现象.但关于重和轻三角形界面不稳定性仍需更加详细的对比研究,特别是轻气柱后期出现的偶极子涡.Dong等[14]对激波与120◦及60◦V形界面作用过程进行实验研究,结果表明不同激波角能诱导不同强度的斜压机制,最终诱导界面产生不同的涡量运动速度,且在60◦界面时所形成的涡更多更清晰.沙莎等[15−17]详细研究了激波与球形R22气柱及梯形SF6气柱作用中射流形成机理与及界面演化过程,发现折射激波聚焦于气柱左侧内部而引导射流,同时气柱上下两侧大量环境气体被卷吸进涡核中.
此外,因Rayleigh-Taylor(R-T)不稳定性常伴随着R-M不稳定性出现[18],它们在天体物理、大气物理、惯性约束核聚变和高速飞行器等领域同样有着非常重要而广泛的应用和研究意义[19].然而,这些领域中物质多呈现第四态(即等离子状态),所以利用磁场来控制界面不稳定性的研究成为近年来的热点和难点.李源和罗喜胜[20]研究了磁场对R-T不稳定性的作用,发现磁场的非线性项对R-T不稳定性有较大影响.磁流体动力学(magnetohydrodynamics,MHD)将流体力学和电磁学结合以描述导电流体在电磁场中的运动,因此本文基于MHD方程组研究磁场对R-M不稳定性的影响.R-M不稳定性中MHD效应的研究起源于磁顶层动力学[21].实验中要获得稳定的等离子体比较困难,因此数值模拟在研究MHD效应对R-M不稳定性的影响中具有十分重要的价值.Samtaney[22]通过对非线性理想磁流体进行二维数值模拟,研究了MHD效应对斜平面R-M不稳定性的影响,并认为磁场可有效控制界面R-M不稳定性,且当磁场方向与激波运动方向一致时,磁场作用于界面斜压涡量,使界面涡量向周围扩散,减少界面上涡量的堆积,从而抑制界面的不稳定性.Wheatley等[23−25]基于不可压线性MHD方程组研究发现当磁场方向与激波的运动方向垂直时,磁场通过干扰间断处激波折射过程,减少界面涡量沉积从而抑制不稳定性的发展.随后,Sano等[26]对平行磁场控制R-M不稳定性的临界磁场强度进行研究,发现临界磁场强度与入射激波马赫数密切相关,并给出了MHD中控制R-M不稳定性临界条件的公式.Cao等[27]通过理论推导,发现在横向磁场下,洛伦兹力作用于界面,抑制界面不稳定性的增长.Mostert等[28]研究了磁场对球形和柱形爆炸中R-M不稳定性的影响.Lin等[29,30]研究了非理想环境下磁场对重质气团爆炸的影响,发现磁场可有效控制R-M不稳定性,且在磁场作用下整个高密度气团会被压缩,同时电阻和双极扩散效应会衰弱磁场的作用,但双极扩散效应还会增大磁压力作用范围.
上述实验研究、数值模拟和理论预测都表明斜压涡量的积累是R-M不稳定性产生的主要原因,斜压涡量是因密度和压力梯度的不一致(斜压效应)而产生.因此对重和轻气柱R-M不稳定性的对比研究十分必要.Dong等[14]的研究证明60◦入射角时,界面产生的涡对更多更清晰,因此本文选取封闭的正三角形气柱进行研究.目前MHD效应对R-M不稳定性的研究多局限于单模重质界面,对于封闭重质和轻气柱的研究仍欠缺.此外,虽然Samtaney[22]对法向磁场作用下MHD效应、对45◦斜平面重质界面R-M不稳定性进行了研究,但是在横向磁场作用下MHD效应对重质和轻质两种界面的作用仍需完善.因此,为了更好地阐明不同介质气柱波系的发展和演化以及磁控下气柱形态演化,本文选取正三角形重质和轻气柱进行研究.采用CTU+CT(corner transport upwind+constrained transport)算法求解MHD方程组[29−31],其中CTU算法用于计算多维积分,CT算法用于保证磁场散度为零.分别对有无磁场情况下激波冲击重质与轻质三角形气柱的过程进行数值研究,详细分析了两种气柱具体波系发展以及界面演化,并对磁场控制界面不稳定性发展的机理进行探讨.最后,定量分析了磁场控制作用下重质和轻质两种界面不稳定性的发展规律.
2 计算方法和模型
本文基于非理想MHD方程组[29,30],采用非分裂的 CTU+CT[31,32]算法进行求解. 其中,CTU(corner transport upwind)算法基于PPM(piecewise parabolic method)对守恒量进行重构,是一种迎风格式的有限体积积分算子.另外,为保证磁场散度为零,在计算Godunov通量时,结合用于计算电场的CT(constrained transport)算法进行通量重构.
图1为平面激波冲击三角形气柱的计算模型.计算域为[−0.01,0.29]× [−0.06,0.06],其长和宽分别为D=0.3 m,H=0.12 m,等边三角形气柱的边长为L=0.07 m.初始时,三角形左顶点与左边界的水平距离为0.01 m,平面入射激波位于左边界上,并随后自左向右传播.重与轻质气柱内分别充满R22和75%(质量分数,下同)He+25%Air的气体,气柱外为空气,内外压力均为1 atm(1 atm=1.013×105Pa).相应气体参数参照表1.
为了更好地反映磁场对气柱变形的控制,计算域的上、下及右边界设为固壁.计算域采用均匀分布的笛卡尔网格,经网格无关性测试后,总网格数为1500×600.本文中,设初始横向磁场强度分别为B=0 T和B=0.01 T,分别对应有控和无控条件,其方向平行于y轴.另外,为了使气体受磁场影响,假设气体已经电离.根据文献[30,31],取等离子体初始电导率为107S/m,热导率为1.4 W/(m·K−1),黏性系数为3.72×10−5Pa/s,霍尔系数为10−7m3/C,双极扩散系数随粒子数密度ρ的增加而减小,因此双极扩散系数为(10−5/ρ)× 10−5m2·Pa·s−1.

图1 模型示意图Fig.1.Schematic of computational model.

图2 激波冲击重质和三角形气柱过程中计算与实验[12,13]纹影图的对比(ds,绕射激波;s1,激波1;tp,三波点;ts,透射激波;ms,马赫杆;sts,二次透射激波) (a)重气柱;(b)轻气柱Fig.2.Comparison of numerical and experimental[12,13]schlieren images of the interactions between shock waves and heavy and light triangular cylinders(ds,dif f racted shock;s1,shock wave1;tp,triple point;ts,transmitted shock;ms,Mach stem;sts,secondary transmitted shock):(a)Heavy cylinders;(b)light cylinders.

表1 气体参数Table 1.Gas parameters
3 结果与讨论
3.1 算例验证
图2为激波冲击重质(a)与轻质(b)三角形气柱的计算纹影图(右)与实验纹影图(左)[12,13]的对比,验证算例的条件均与相应的实验条件一致.可见,本文数值方法捕捉到的入射、反射、折射和透射等复杂波系以及气柱形态的演化均与相应的实验结果符合.另外,本文结果能更清晰地反映出重气柱内三波点处的滑移线以及轻气柱外三波点处的滑移线.
3.2 无磁场时重气柱
图3为无磁场控制(B=0 T)下,激波与重气柱作用过程的计算纹影图.图4为不同时刻流场压力与速度分布图,其中A为气柱左顶点,B为绕射激波聚焦点,C1,C2为气柱上下角.由图3(a)可见,入射激波is冲击气柱时,其中间段因入射角为零,在气柱左顶点发生透射,在气柱内产生透射激波ts.且因重质气体声阻抗大,ts的传播速度小于is.同时,入射激波is的上下两段分别在气柱上下界面发生正规折射(regular refraction,RRR),形成弧形反射激波crs与折射激波ras.随后,气柱内ras和ts相互作用产生激波s1和两个三波点tp以及三波点处的滑移线.
入射激波is与弧形反射激波crs向下游传播的过程中,持续与气柱上下界面发生作用,诱导界面出现R-M不稳定性(图3(b)—(e)).另外,因重质气体的阻挡作用,气柱外侧气体波后速度大于气柱内波后速度(图4(a)),K-H不稳定性开始出现.因此在斜压效应与K-H不稳定性的共同作用下,气柱左顶点卷起形成向外翻转的涡对,如图3(b)所示.因此气柱上下界面在R-M与K-H不稳定性的共同作用下,开始失稳并逐渐卷起形成珠状小涡序列(图 3(b)—(f)).
当is绕过C1与C2后,形成绕射激波ds,其一端在下游界面与ras相连,另一端则与is相连(图3(b)),且绕射过程中还会形成向上游传播的膨胀扇ps.同时,折射激波ras作用于下游界面,在气柱内产生反射稀疏波rrs(图3(b)).由于C1与C2处存在较大的剪切速度(图4(b)),因此气柱上下角在斜压效应和K-H不稳定的共同作用下卷起形成涡对,并最终发展成为两个主涡(图3(b)—(g)).
随着ts向下游传播(图3(a)—(c)),其长度不断增大,同时折射激波ras不断缩短并在t=230µs时消失.当ts穿过下游界面时,分别形成向下游与上游传播的弧形透射激波cts与弱反射激波ws(图3(d)).此时rrs穿过s1,并继续向气柱中心运动(图3(d)),同时其波后产生局部低压区(图4(b)).
t=240µs时,上下两条绕射激波ds在中心轴上聚焦并反射,形成反射激波drs(图3(e)),同时cts被分成上下两段(图3(e)).绕射激波ds聚焦(图3(e))时,聚焦点B后产生局部高压区,对下游界面造成瞬间的强冲击,导致碰撞区界面的流场速度瞬间上升,诱导气柱界面的局部变形(图3(f)),并逐渐形成一道向下游传播的蘑菇状射流(图3(g)).

图3 无磁场时,激波与重气柱作用过程的计算纹影图 (brs,尾壁反射激波;crs,弧形反射激波;cts,弧形透射激波;is,入射激波;ps,膨胀扇;ras,折射激波;rrs,反射稀疏波;ws,弱反射激波) (a)t=110µs;(b)t=190µs;(c)t=220µs;(d)t=230µs;(e)t=240µs;(f)t=330µs;(g)t=1080µs;(h)t=1900µsFig.3.Schlieren image sequences of interaction between shock wave and heavy cylinder without a magnetic f i eld(brs,back wall ref l ected shock;crs,curved ref l ected shock;cts,curved transmitted wave;is,incident shock;ps,expansion fan;ras,refracted shock;rrs,rarefaction wave;ws,weak shock):(a)t=110µs;(b)t=190µs;(c)t=220µs;(d)t=230µs;(e)t=240µs;(f)t=330µs;(g)t=1080µs;(h)t=1900µs.
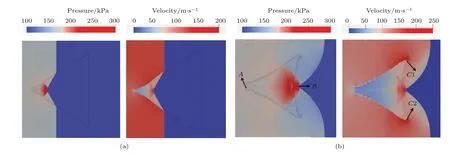
图4 不同时刻压力(左)和速度(右)云图 (a)t=90µs;(b)t=240µsFig.4.Cloud chat of pressure(left)and velocity(right)at dif f erent time:(a)t=90µs;(b)t=240µs.
由图3(f)可知,气柱内的s1,rrs与ws在气柱上下界面间来回碰撞,在气柱内形成复杂的波系结构.期间,复杂波系与界面上小涡序列多次相互作用,加速了界面的失稳而形成复杂的涡结构(图3(f),(g)),从而加剧了重质气体与环境气体的混合.此外,在t=1080µs后 (图3(g)),入射激波在右边界反射而回传的尾壁反射激波brs到达气柱尾部,随后再次与气柱发生作用,加剧了气柱界面的失稳,使气柱形状更为复杂,如图3(h)所示.
3.3 无磁场时轻气柱
图5为无磁场时,激波与轻气柱作用过程的计算纹影图.图6为不同时刻,流场速度分量云图.由图5(a)可知,入射激波is冲击气柱后,在气柱内产生透射激波ts1.由于轻气柱声阻抗小,ts1的传播速度大于is,在气柱外产生自由前导激波fps.该自由前导激波fps在界面外与入射激波is发生自由前导折射(free precursor refraction,FPR)[13,34],伴随着一系列反射稀疏波rrw,形成向上游传播的弧形反射激波crs、与界面相连的激波sk以及滑移线sl.
以复合改性植物胶为稠化剂,有机络合物为交联剂,引入抑制剂进一步控制缓交时间,并添加少量表面活性剂提高解堵后破胶液的排液能力,形成了暂堵压井胶塞配方,见表1。
因轻气柱声阻抗小,is冲击气柱左顶点后,压缩顶点向下游运动,并在顶点处形成一个向下游运动的高速区,如图6(a)所示.该高速区持续作用在气柱上游顶点上,最终形成一个反相空气射流结构(图 5(a)—(h)).
ts1穿过下游界面时,形成向下游传播的二次透射激波ts2与向上游传播的弱激波ws,此时fps绕过气柱上下角与ts2相连(图5(b)).在t=170 µs时,弱激波ws到达气柱左顶点形成的空气射流涡环处,并与射流涡环相互作用.但因射流涡环上下涡核的旋向相反,弱激波被剪断成3段(图5(c)).随着fps离开界面,FPR会转变为由fps,is,激波sn,马赫杆ms以及三波点tp组成的双冯·诺依曼折射(twin von Neumann refraction,TNR)[13,34](图5(d)).
t=190µs时,反射激波crs到达计算域的上下边界,并发生碰撞反射,形成的反射激波bs向气柱中心轴运动.在t=260µs时,反射激波再次跟气柱作用,但因气柱内外声阻抗不同,壁面反射激波bs被剪成3段(图5(e)),其中气柱内段传播较快.气柱内复杂波系在t=800µs时基本耗散.t=1050µs时,入射激波在右边界反射而回传的尾壁反射激波brs冲击气柱.由此可见,相对于重气柱,激波与轻气柱作用过程中激波结构及界面演变完全不一样,重气柱内的激波呈汇聚趋势,而轻气柱内激波发散.
由图5(d)—(f)可知,气柱左顶点处的射流结构形成后,向下游运动的同时不断将气柱上下界面卷入到射流的反向涡环内,使涡环尺度持续增大同时,在反相空气射流的拖动下,界面在y方向产生较大的剪切速度(图6(b)),因此在K-H不稳定作用下,射流尾部气柱界面开始失稳并卷起涡串(图5(e),(f)).随着界面的发展,射流涡前端面与下游界面的距离越来越近(图5(d)—(f)),并在t=800µs时穿透下游界面,形成向下游运动的偶极子涡[33],同时下游界面几乎被分割成对称的两半,如图5(f)所示.随后,尾壁反射激波brs冲击气柱,进一步加强了气柱界面的失稳,使界面上的大涡结构破碎形成复杂的湍流涡结构(图5(h)).

图5 无磁场情况下,激波与轻气柱作用过程的密度纹影图(bs,壁面反射激波;fps,自由前导激波;rrw,反射稀疏波;sk,激波k;sl,滑移线;sn,激波n;ts1,一次透射激波;ts2,二次透射激波) (a)t=110µs;(b)t=150µs;(c)t=170µs;(d)t=190µs;(e)t=260µs;(f)t=800µs;(g)t=1050µs;(h)t=1900µsFig.5.Density schlieren image sequences interaction between shock wave and light cylinder without a magnetic fi eld(bs,wall re fl ected shock wave;fps,free precursor shock;rrw,re fl ected rare shock;sk,shock wave k;sl,slip line;sn,shock wave n;ts1, fi rstly transmitted shock;ts2,secondary transmitted shock):(a)t=110µs;(b)t=150µs;(c)t=170µs;(d)t=190µs;(e)t=260µs;(f)t=800µs;(g)t=1050µs;(h)t=1900µs.
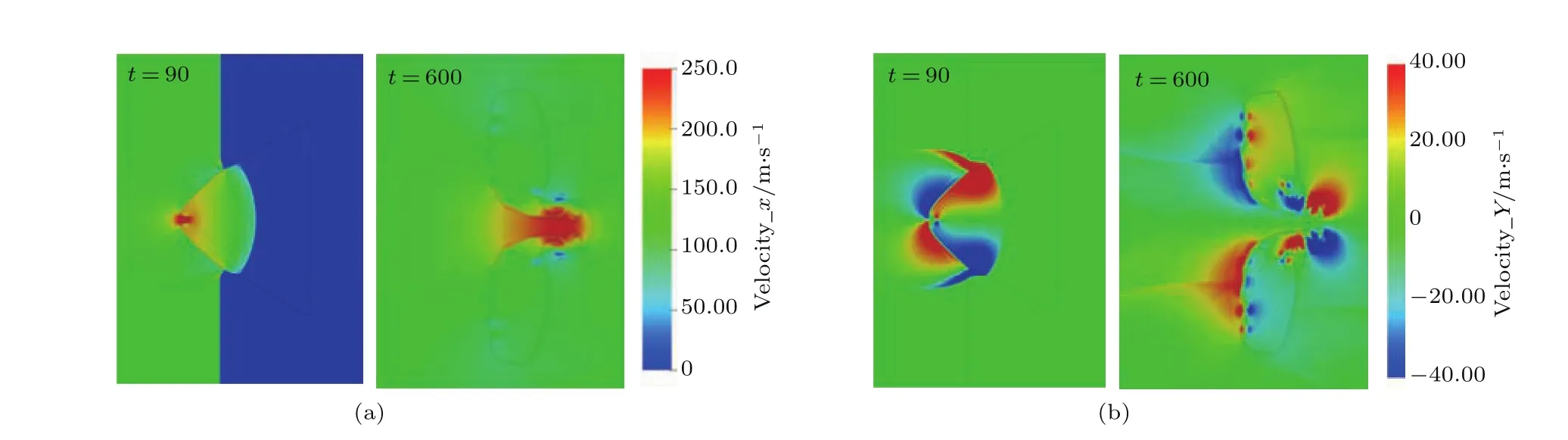
图6 t=90µs和t=600µs速度分量云图 (a)x方向的速度分量;(b)y方向的速度分量Fig.6.Velocity components cloud chart at t=90 µs and t=600 µs:(a)Velocity component of x direction;(b)velocity component of y direction.
图7 为两气柱中轴线上压力和速度曲线图,其中实线为重气柱,虚线为轻气柱.结合图3与图7可知,重气柱相当于一个凸透镜,使激波在内部汇聚,形成高压区;而轻气柱相当于一个凹透镜,使激波发散,因而轻气柱内部压力不高.对于重气柱,绕射激波ds聚焦时(t=240µs),在中轴线上产生320 kPa的高压,膨胀波rrs气柱内产生175 kPa的相对低压(图7(a)),气柱界面两边极大的压差导致下游界面形成介质射流.而轻气柱,其左顶点在激波撞击后产生高速向下游运动,速度为280 m/s,从而导致反向空气射流的形成.此外,重气柱内波系汇聚且持续与气柱界面作用,所以R-M不稳定是重气柱失稳的主要原因,这也与Luo等[13]的结果一致.对于轻气柱,虽然波系在气柱内发射,但入射激波作用下产生的高速射流头部会在界面两侧产生较大的剪切效应,因此K-H不稳定性在轻气柱失稳过程中占主导作用.

图7 不同时刻,气柱对称轴上压力和速度沿轴线的分布(H重气柱;L轻气柱) (a)压力;(b)速度Fig.7.Distributions of pressure and velocity along symmetric axis at dif f erent time(H,heavy cylinders;L,light cylinders):(a)Pressure;(b)velocity.
3.4 有磁场时界面演化
图8 为加入B=0.01 T横向磁场后,激波与两种介质三角形气柱作用过程的计算纹影图.其中上图为重气柱,下图为轻气柱.在磁场作用下,流场波系结构及演化与无磁场时一致(图3和图5),因而不再缀述且无磁场时的数值结果与相应的实验结果符合,可以保证本文算法对磁场作用下激波与界面作用过程模拟的准确性.由图8可知,在磁场作用下,重气柱除了上下角因斜压效应而卷起形成的涡以及下游边界中心形成的射流结构外,其余界面保持光滑,射流涡的表面也变得光滑(图8(a1)—(d1));轻气柱空气射流头部变得光滑,偶极子涡对也消失(图8(a2)—(d2)).
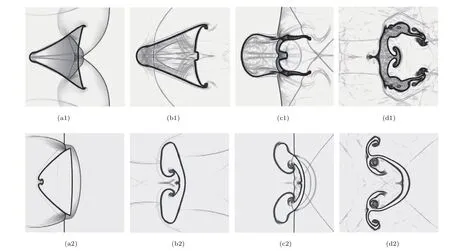
图8 磁场控制下(B=0.01 T),激波与重质(上)和轻质(下)气柱作用过程的密度纹影图 (a1)t=240µs;(b1)t=400µs;(c1)t=1200 µs;(d1)t=1900 µs;(a2)t=150 µs;(b2)t=600 µs;(c2)t=1050 µs;(d2)t=1900 µsFig.8.Density schlieren image sequences of the shock wave interaction with heavy(upper)and light(lower)cylinder under magnetic f i eld control(B=0.01 T):(a1)t=240µs;(b1)t=400µs;(c1)t=1200µs;(d1)t=1900µs;(a2)t=150µs;(b2)t=600µs;(c2)t=1050µs;(d2)t=1900µs.
图9(a)和图9(b)为有无磁场情况下,气柱界面涡量的分布云图,其中上图为重气柱 (400µs),下图为轻气柱(200µs).重气柱密度梯度垂直界面指向下游,压力梯度垂直波阵面指向上游,在斜压效应的作用下,重气柱上界面附近流体顺时针旋转生成负涡量,相应的下界面处流体逆时针旋转生成正涡量,而轻气柱则相反,具体涡旋方向如图1所示.由图9可知,无磁场时,斜压涡量沉积在界面上(图9(a)),并不断诱导界面卷起小涡序列进而失稳.加入横向磁场后,涡量不再沉积于界面,而是在界面两侧形成相互远离的涡层(图9(b)).
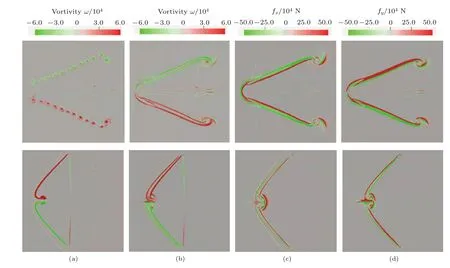
图9 涡量和洛伦兹力云图(上图:重气柱,t=400µs;下图:轻气柱,t=200µs)(a)Vorticity(B=0 T);(b)vorticity(B=0.01 T);(c)Lorentz force(y);(d)Lorentz force(x)Fig.9.Vorticities and Lorentz force distribution(upper,heavy cylinder,t=400µs;lower,light cylinder t=200µs):(a)Vorticity(B=0 T);(b)vorticity(B=0.01 T);(c)Lorentz force(y);(d)Lorentz force(x).

图10 两气柱界面涡旋方向和洛伦兹力f的方向 (a)重气柱;(b)轻气柱Fig.10.Directions of rotating vorticities and Lorentz forces f on the cylinder interfaces:(a)Heavy cylinder;(b)light cylinder.
为了进一步从理论上分析磁场作用下涡量不能沉积在界面的机理,以间断面为参考坐标系,考虑动量和切向电场的守恒关系式[35]:

其中方括号代表界面两侧的差值;下标n和t分别代表法向和切向分量;ρ代表密度;Bn,Bt分别代表法向和切向磁场强度;vn,vt分别代表法向和切向速度.连续间断面上vn=0,且界面上Bn=0,由(1),(2)式可得[vt]=[Bt]=0.因此连续间断面上不能存在涡层和电流层[26].尽管激波冲击气柱的瞬间会在气柱界面上产生涡量,随后该涡量也会在磁场作用下远离界面.
Samtaney等[22−25]对界面附近激波折射过程进行详细的研究后发现,在磁场作用下,激波折射过程会产生MHD波.Samtaney[22]对平面激波冲击45◦斜平面的研究表明,激波冲击界面产生的反射激波在磁场作用下会转变为一对慢反射和快反射磁声波(一种MHD波),透射激波转变为一对慢透射和快透射磁声波.另外,涡量在磁场作用下不再沉积于界面,而是分布在慢反射和慢透射MHD波上.本文两种介质封闭三角形界面较Wheatley和Samtaney的单模重质界面更为复杂,产生的波系结构和射流现象也复杂多变,因而更具有研究前景和价值.从图11的磁力线和密度分布图(100µs)可知,在激波干扰下,界面附近磁力线扭曲.一方面扭曲的磁力线会产生阿尔文波(一种慢MHD横波).另一方面扭曲的磁力线会增大平行于界面的磁分量,从而在界面两侧产生较大的洛伦兹力[27].最终界面涡量在洛伦兹力的作用下形成相互远离的涡层(图9(b)),该涡层将附于Alfvén波上,并随着Alfvén波逐渐远离界面,最终界面因缺少涡量沉积而稳定.

图11 两气柱磁力线和密度分布图 (a)重气柱;(b)轻气柱Fig.11.Spatial distribution of magnetic f i eld lines and density of two gas cylinders:(a)Heavy cylinder;(b)light cylinder.
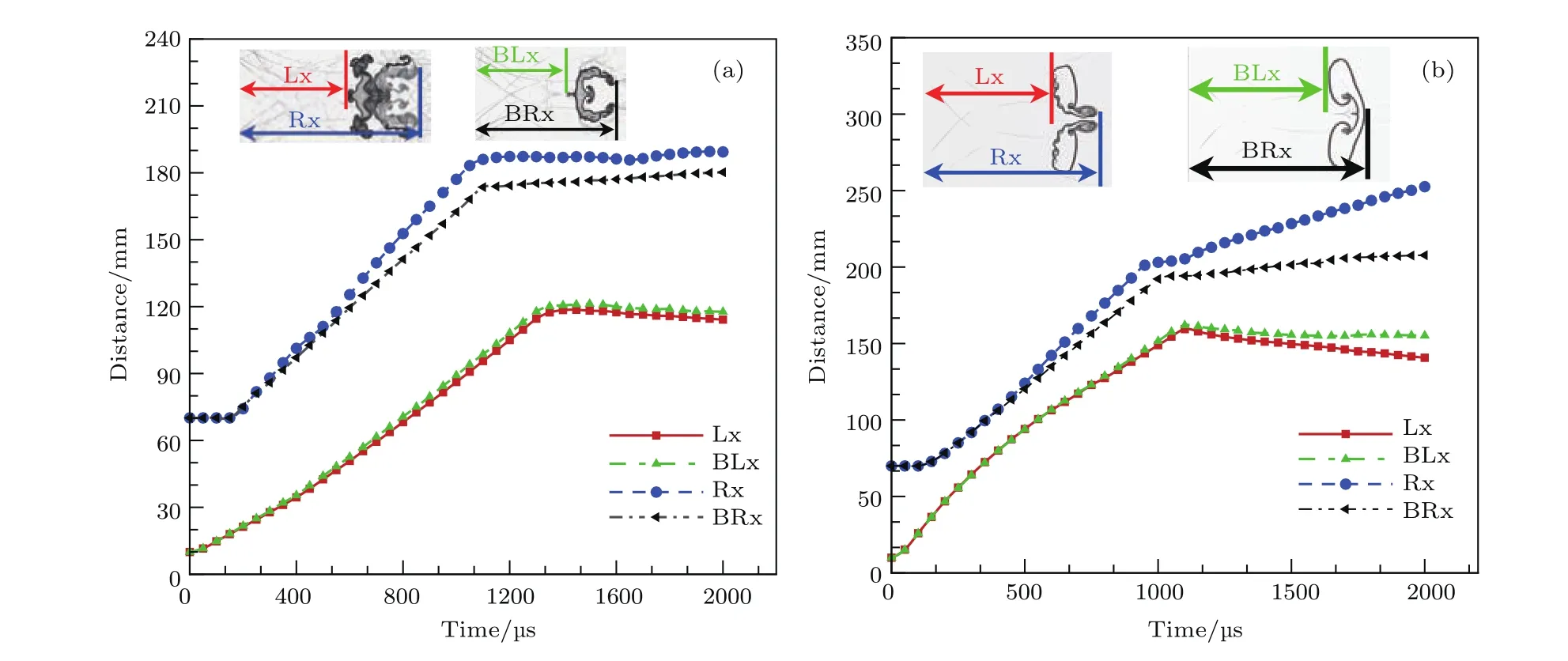
图12 激波与气柱作用过程中气柱上下游界面运动情况 (a)重气柱;(b)轻气柱Fig.12.Movement of upper and lower interfaces during the interaction of a planar shock wave and cylinder:(a)Heavy cylinder;(b)light cylinder.
图12 为气柱界面与左边界距离随时间的变化曲线.无磁场控制时,两气柱上游界面(Lx)均以恒定的速度向下游运动[13,14],但因轻质气体的声阻抗小,其速度更快.下游界面(Rx)则在入射激波到达前静止,随后同样以恒定的速度向下游运动[12,13].加入磁场后(BLx与BRx),BLx与Lx基本重合.然而,磁场会阻止气柱上下角处涡结构的进一步卷起,因此在上下角卷起涡结构后(t>400µs),BRx与Rx的差距逐渐加大.线图中拐点(t≈1100µs)为尾壁反射激波冲击气柱时刻,可见磁场使拐点后下游界面基本不动.由此可知,磁场可有效控制气柱的运动,且对轻气柱界面运动具有更好的控制效果.
图13和图14则分别为重与轻气柱纵向和横向尺寸随时间的变化,图中拐点(t≈1100µs)为尾壁反射激波冲击气柱所致.对于重气柱(图13),磁场可有效抑制界面两个特征尺度的变形.但对于轻气柱(图14),磁场能有效控制纵向尺寸L的变化,却并不能控制横向尺寸H的变化.由此可知,磁场对重气柱变形的控制效果更好.
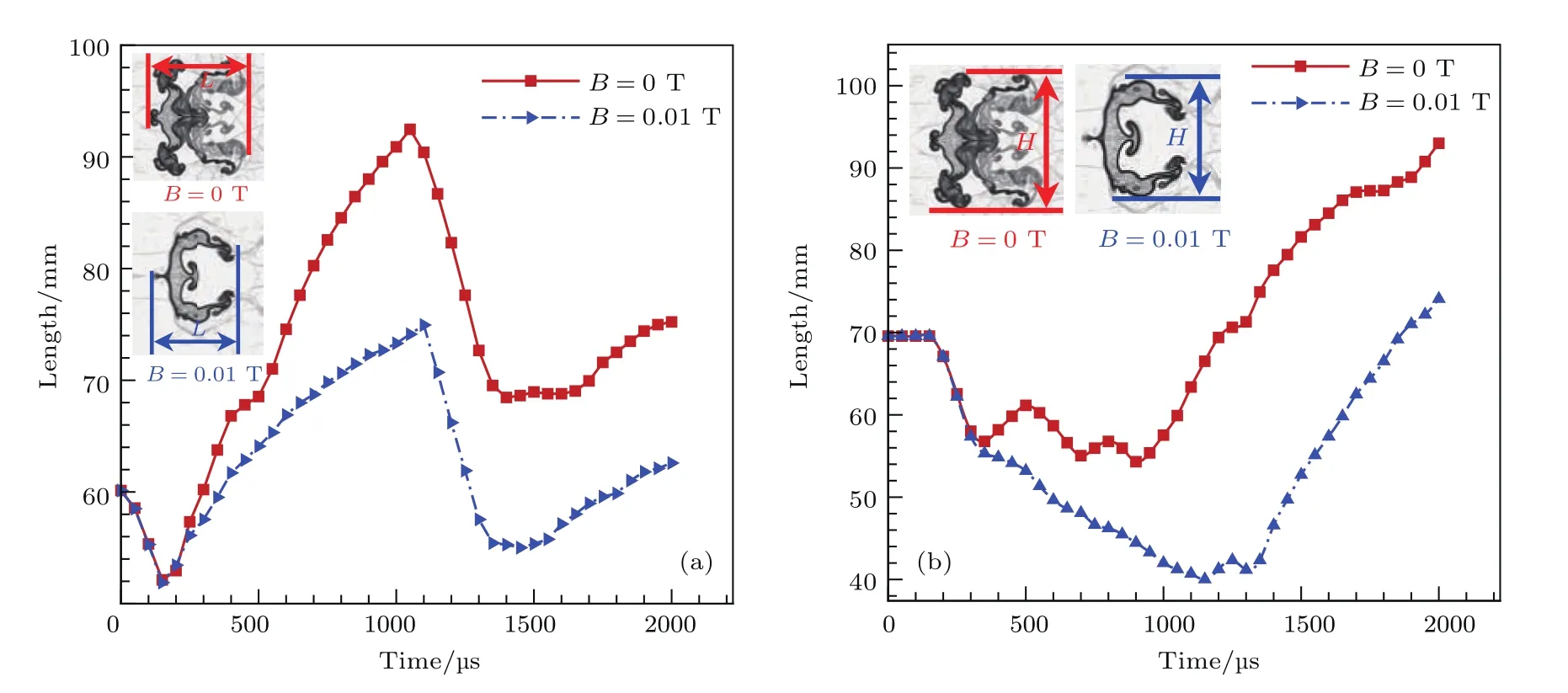
图13 激波与重气柱作用过程中长度L和高度H的变化情况 (a)纵向长度L;(b)横向高度HFig.13.Development of length L and height H of the triangular interface during the interaction between shock waves and heavy cylinder:(a)Length L;(b)height H.
4 结 论
本文基于非理想MHD方程组,为保证磁场散度为零,采用非分裂的CTU+CT算法分别对有无磁场情况下激波冲击重质和轻质三角形气柱的过程进行数值研究.得到以下结论.
无论有无磁场,激波与重质或轻气柱相互作用的过程中均具有不同的波系结构和射流现象.具体而言,入射激波与重气柱作用时发生常规折射,气柱相当于一个凸透镜,使复杂波系在气柱内汇聚;入射激波与轻气柱作用时则发生非常规折射,气柱相当于一个凹透镜,使复杂波系经过气柱后发散.另外,绕射激波在重气柱中心轴上聚焦产生局部高压,诱导重气柱下游界面中心处出现介质射流;而入射激波与轻气柱作用时,轻气柱左顶点卷起形成空气射流.
无磁场时,重气柱上下角卷起形成主涡对,轻气柱空气射流会穿过下游界面形成相互分离的偶极子涡.同时,两气柱界面均出现大量次级涡序列.此外,对于重气柱,因气柱内波系汇聚并持续与界面作用,R-M不稳定性在其失稳过程中占主导地位;而对于轻气柱,后期气柱内波系耗散,射流头部运动较快,K-H不稳定性在失稳过程中占主导地位.
施加磁场后,洛伦兹力作用于界面涡量,将涡量向界面两侧输运,减少界面涡量沉积,抑制界面卷起失稳.最终界面两侧会形成两个相互远离的涡层,该涡层附于Alfvén波上,并随着Alfvén波远离界面.最终,在磁场作用下,重气柱的主涡对、轻气柱的偶极子涡以及两气柱界面次级涡序列也消失,界面不稳定性得到控制.最后定量分析表明,磁场能有效控制气柱界面的运动,且对轻气柱界面运动具有更好的控制效果.此外,磁场可控制重气柱纵向与横向两个特征尺寸的增长,却不能控制轻气柱的横向尺寸的增长.

