激波诱导双层气柱演化的偏心效应研究
冯莉莉, 翟志刚, 司 廷, 罗喜胜
(中国科学技术大学近代力学系, 安徽合肥 230027)
引言
当有扰动的界面受到瞬时冲击时, 界面上的初始小扰动会在斜压机制和压力扰动机制的驱动下不断发展, 导致二次不稳定性及大量小尺度涡结构的产生, 并最终可能形成湍流混合, 这种现象称为Richtmyer-Meshkov (RM)不稳定性[1-2]. RM不稳定性在惯性约束核聚变(inertial confinement fusion, ICF)[3]、 超声速燃烧[4]和超新星爆发[5]等大量的工程实际和自然现象中具有重要的应用价值[6], 自从被提出以来就备受关注.
在RM不稳定性的研究中, 激波与气柱相互作用一直是研究热点. Haas等[7]采用硝化纤维膜技术生成氦气柱和R22气柱, 利用几何声学对激波作用后气柱内外的波系结构进行了预测并分析了界面的演化过程. Picone等[8]数值研究了激波与气柱相互作用过程, 提出了预测界面沉积环量的PB模型. 为了消除硝化纤维膜技术中膜和支杆对流场的影响, Jacobs[9-10]使用射流技术生成了无膜轻气柱和重气柱, 并采用平面激光诱导荧光技术(planar laser-induced fluorescence, PLIF)获得了更详细的流场信息. 之后, Tomkins等[11]利用PLIF技术测量了激波作用无膜气柱后气体间的混合速率. 王兵等[12]数值研究了RM不稳定性诱导混合的参变机理, 发现较大的界面振幅和激波强度会导致更强的涡量场, 强化物质混合. 张赋等[13]采用射流技术结合粒子图像测速技术(particle image velocimetry, PIV)探究了反射激波作用重气柱的演化过程, 发现反射激波冲击界面后会产生与初始涡环旋转方向相反的次级涡环结构. 除了圆形气柱, 射流技术还可以生成具有不同纵横比的椭圆气柱[14-15], 结合数值模拟[16], 椭圆形的轻、 重气柱得到了充分研究. 但由于气体扩散严重, 无膜气柱界面较厚, 初始条件难以控制. Wang等[17]采用肥皂膜技术生成了形状精确可控的二维间断型SF6气柱, 分析了被激波冲击后, 气柱内部的波系结构和上游界面的位移. 基于该方法, Ding等[18-19]在实验中生成了具有不同曲率的三维气柱, 研究了平面激波冲击下三维气柱的演化过程, 重点讨论了三维性对涡量分布和界面演化的影响. 此外, Ou等[20]对重气柱中Atwood数的影响进行了定量研究, 指出射流类型取决于激波聚焦的位置.
作为对单气柱的拓展, 激波作用于多个气柱也得到了广泛关注, 气柱间的耦合作用使得多气柱问题变得更加复杂. 基于射流技术, Tomkins等[21-23]发现, 当激波作用于双气柱后, 会产生一个内涡对和一个外涡对. 受无膜界面扩散性的影响, 实验中的外涡对尺寸大于内涡对尺寸, 与数值结果中内、 外涡对尺寸大小相等有较大差异. Zhai等[24]和Zou等[25]分别用肥皂膜技术和射流技术生成了不同间距的双圆气柱和双椭圆气柱, 重点关注了气柱间距对界面演化的影响. 之后, 廖深飞等[26]采用PIV技术获得了双椭圆气柱在平面激波冲击下的速度场、 涡量场和环量, 定量描述了界面耦合作用. Kumar等[27]将3个重气柱排列为不同形状, 探究了排列顺序对激波冲击后3气柱流场结构的影响.
以往的研究多集中于激波与单层气柱的相互作用, 但在实际应用中多层界面广泛存在. 比如, ICF的靶丸包含着多层材料, 超燃冲压发动机中燃油雾化的液滴包含着空气腔, 所以研究激波冲击下多层界面的演化具有重要意义. Mikaelian[28-31]研究了有限厚度气层的RM不稳定性, 并提出了预测振幅增长率的解析解. Jacobs等[32-34]用射流技术生成了气帘界面, 基于涡模型提出了预测气层整体混合宽度增长的非线性理论. 在已有研究中, 气帘技术是生成准平面流体层最常用的方法, 但是气帘内部气体浓度不均匀[35-36], 而且射流技术产生的界面较厚, 三维性较强. Liang等[37-38]利用肥皂膜技术生成的SF6气层克服了这些难题, 他们量化了界面耦合机制以及气层内来回反射的波系对气层演化的影响, 并修正了Mikaelian[28,30]提出的扰动增长模型.
在ICF中, 靶丸是一个多层球形结构, 与气层存在一定的差异. 当球形激波冲击靶丸后, 靶丸内部不同材料界面上的小扰动不断增长, 不同材料之间发生的混合降低了内层燃料的浓度, 最终可能导致点火失败. 因此, 研究多层球形界面的RM不稳定性十分重要. 但是在实验中很难生成多层球形界面, 而且界面之间的耦合作用和可压缩效应会使问题变得更加复杂, 所以目前这方面的研究还比较缺乏. 作为对该问题的简化, Ding等[39-41]研究了半环形轻、 重气层在汇聚激波冲击下的演化过程, 发现界面厚度对Rayleigh-Taylor (RT)效应和界面耦合有着很大的影响, 导致不同情况下界面扰动振幅增长存在较大差异. 在汇聚情况下, 几何效应、 RT效应、 RM不稳定性和可压缩效应会耦合在一起, 导致界面演化十分复杂. 为了简化分析, 将三维双层球形界面简化为二维双层圆柱界面, Wang等[42]数值研究了平面激波与同心双层圆气柱相互作用过程, 并提出了一个环量预测模型. 随后Feng等[43]开展了相应的实验研究, 考察了内层气柱半径变化对流场的影响. 结果发现内层气柱的存在会改变气柱内的波系结构, 来回反射的波系导致气柱上游界面被反复加速, 在演化后期内外层气柱存在耦合作用, 随着内层气柱半径的增大, 耦合作用增强.
但是同心双层气柱只是一种理想模型. 实际上, 由于加工误差, ICF靶丸中各层材料很难保证绝对同心, 各层材料的球心不可避免地会存在一定偏差. 此外, 超声速燃烧中燃油雾化液滴内部的空气泡也很难恰好处于液滴的球心. 激波与嵌入空腔的水滴相互作用的研究[44]表明, 内部空腔位置对外部水滴变形有较大的影响, 而且当内部空腔靠近液滴上游界面时, 会阻碍外部液滴位移的发展. 因此, 研究偏心效应对双层气柱的演化影响具有重要意义. 本文基于肥皂膜技术和高速纹影法, 在平面激波管中开展了双层气柱演化的实验研究, 分析了双层气柱演化过程中偏心效应的影响, 获得了内、 外层气柱的尺寸和上游极值点位移的变化情况; 并通过数值模拟手段分析了双层气柱内部的物质混合与界面沉积环量的变化规律, 将几种经典的环量模型线性叠加来预测双层气柱的环量.
1 实验与数值方法
1.1 实验方法
在之前的工作中[43], 通过改进肥皂膜技术成功生成了不同半径比的同心双层气柱, 本文采用同样的方法生成偏心双层气柱. 实验之前, 在两块厚度为3 mm的亚克力板上雕刻出双层气柱的轮廓(宽0.5 mm, 深1 mm的两个圆形凹槽), 并将亚克力板粘成与实验段匹配的高度为10 mm的“盒子”. 准备两个如图1(a)所示的储气装置, 分别标记为1, 2. 装置1充入SF6, 装置2充入空气. 将装置1的导管蘸上肥皂液后放入内圆的圆心处, 打开阀门1, 形成一个充满SF6的肥皂泡. 由于SF6的密度大于空气, 肥皂泡首先附着在下板, 随着肥皂泡内SF6增多, 肥皂泡体积不断膨胀, 上界面接触到上板后形成SF6气柱. 此时, 关闭阀门1, 打开阀门2可以用注射器将多余的SF6抽出, 使SF6气柱的轮廓位于两个凹槽之间. 之后将装置2的导管蘸上肥皂液伸入形成的SF6气柱内部, 打开阀门1在SF6气柱内部形成一个空气气柱, 随着内部空气增多, 外层气柱也会随之膨胀, 最终内、 外层气柱分别被之前雕刻的凹槽约束, 形成一个二维双层气柱, 如图1(b)所示. 与Wang等[17]用细线约束肥皂泡的方法相比, 本文采用的约束槽消除了细线对肥皂膜界面演化的影响, 而且之前的研究[43]表明, 凹槽对实验的影响很小, 可以忽略.
为探究偏心效应对流场演化的影响, 本文固定外层气柱半径R=28 mm, 内层气柱半径r=14 mm, 改变内层气柱在流向上的位置得到3种双层气柱, 其截面如图1(c)所示. 将内层气柱向上游偏移距离记为d=-7 mm, 向下游偏移距离记为d=+7 mm.由于肥皂膜不能完全隔绝气体, 环内的SF6会进入内层气柱, 而内层气柱的空气和外面的环境气体也会进入环内, 使得实验气体会受到一定程度的“污染”. 由于气柱对称轴处的激波变形较小, 可以通过此处入射激波和透射激波的速度, 结合一维气体动力学理论计算出内层气柱和气环中SF6的浓度[7]. 根据从实验图片获得的入射激波和透射激波速度计算出的各工况气体浓度及其他物理参数在表1中给出. 其中,d表示内层气柱的偏心距离,VF1和VF2分别表示环内和内层气柱中SF6的体积分数.

(a) Schematic of the device to generate double-layer gas cylinder
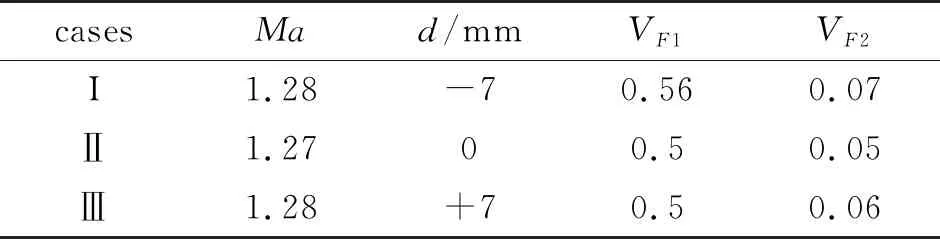
表1 各组工况的物理参数
本实验是在水平激波管中进行的. 激波管由高压段(1.9 m)、 低压段(1.0 m)、 转换段(1.0 m)和实验段(0.4 m)组成, 实验段的尾端为开口, 消除了反射激波的影响. 实验段的横截面积为136 mm×10 mm, 即气柱高度为10 mm, 小于Wang等[17]实验中气柱的高度, 有效减小了气柱的三维效应. 利用压力传感器或者入射激波纹影图像测得入射激波Mach数为1.28±0.01. 本实验采用高速相机(FASTCAM SA5, Photron Limited)结合纹影系统对流场进行捕捉, 采用氙灯光源(CEL-HXF300)照射流场, 高速相机的拍摄速度为50 000 fps, 曝光时间为1 μs, 纹影图片的空间分辨率为0.345 mm/pixel. 在实验之前, 对边界层质量流量亏损厚度(位移厚度)δ*进行估计
(1)
其中,x(~120 mm)为界面在流向方向上运动的最大位移, Δv(~108 m/s)为激波冲击后界面的阶跃速度. 为了简化计算, 假定环境气体和内层气柱中是纯空气, 环内是纯SF6, 在实验温度为290 K时, 空气(SF6)的黏性系数μ和密度ρ分别为μ=1.83×10-5, 1.6×10-5Pa·s,ρ=1.204, 6.143 kg/m3.用式(1)计算出边界层厚度δ*为0.09~0.2 mm, 远小于气柱的高度(10 mm). 如果考虑气体污染, 边界层厚度会更薄. 因此, 边界层影响可以忽略不计.
1.2 数值方法
为了获得更详细的流场信息, 本文采用高阶WENO格式与双通量算法结合的HOWD程序[19]对激波冲击双层气柱进行数值模拟. 不考虑化学反应, 忽略气体的黏性, 采用二维Euler方程对流场演化进行求解, 控制方程为
其中,U表示混合气体的守恒变量,F和G代表x和y方向的流通量, 表达式为

其中,ρ和ρ1分别表示混合物、 单组分气体的密度,p表示混合气体的压力,u和v分别表示气体沿x和y方向的速度,E表示单位体积流体的总能量. 该程序的可靠性已经在之前的研究中得到了充分验证[19-20,43,45].
计算域的设置(275 mm×136 mm)与实验的有效区域保持一致, 如图2所示. 上下边界设为固壁, 左右边界设为开口, 初始温度T0和压力p0分别为293 K和101 325 Pa. 为验证网格收敛性, 本文设置了0.8, 0.4, 0.2和0.1 mm这4种尺寸的网格对工况I进行数值模拟, 图3为激波作用气柱后146 μs时刻沿中心线的密度分布情况. 结果表明, 随着网格变密, 结果逐渐收敛. 为保证计算的精度, 本文采用0.1 mm的网格进行数值模拟, 并将数值结果与实验结果进行对比.

图2 计算域示意图

图3 不同网格尺寸下, 激波冲击气柱后146 μs时, 沿双层气柱中心线的密度分布情况
2 结果与讨论
2.1 界面演化与波系
图4~6展示了内层气柱在不同位置的3种双层气柱被平面激波冲击后演化的实验与数值纹影图. 无量纲时间τ=tWi/D0, 其中Wi为入射激波速度,D0为外层气柱直径, 将激波刚作用外层气柱上游界面时刻记为τ=0.以工况 Ⅰ 为例描述流场波系结构和界面形态演化. 当入射激波(incident shock wave, IS)作用于外层气柱的上游界面时, 会产生一次透射激波(first transmitted shock wave, TS1), 在气环内向下游运动, 还会产生一次反射激波(first reflected shock wave, RS1), 在环境气体中向上游传播, 同时上游界面获得初速度向下游运动, 外层气柱被压缩(τ=0.2).紧接着, 部分TS1与内层气柱上游界面相互作用, 在早期二者夹角较小, 发生规则折射, 产生二次透射激波(second transmitted shock wave, TS2), 在内层气柱内向下游运动, 还会产生一次反射稀疏波(first reflected rarefaction wave, RW1), 在气环内向上游传播, 同时内层气柱被压缩(τ=0.51).未进入内层气柱的TS1继续在环内向下游传播. 随着TS1向下游移动, TS1与内层气柱的夹角增大, 规则折射逐渐转变为非规则折射. 由于内层气柱中空气的声阻抗小于环内SF6的声阻抗, TS2的传播速度大于环内的TS1, 在内层气柱附近会产生自由前驱激波(free-precursor shock wave, FPS). FPS与TS1相互作用, 产生二次反射激波(second reflected shock wave, RS2)和连接着内层气柱的激波K. 4道激波(TS1, RS2, FPS和K)相交于同一点(即四波点, quadruple point, QP), 波系示意图如图7(a)所示, 此时的波系类型为自由前驱激波折射(free precursor refraction, FPR)[46]. 随着TS1与内层气柱的夹角进一步增大, 4道激波不再相交于一点, 四波点变为两个三波点(triple point, TP)并通过Mach杆连接, 此时的波系结构为双Von Neumann折射(twin Von Neumann refraction, TNR)[46], 其波系示意图如图7(b)所示.
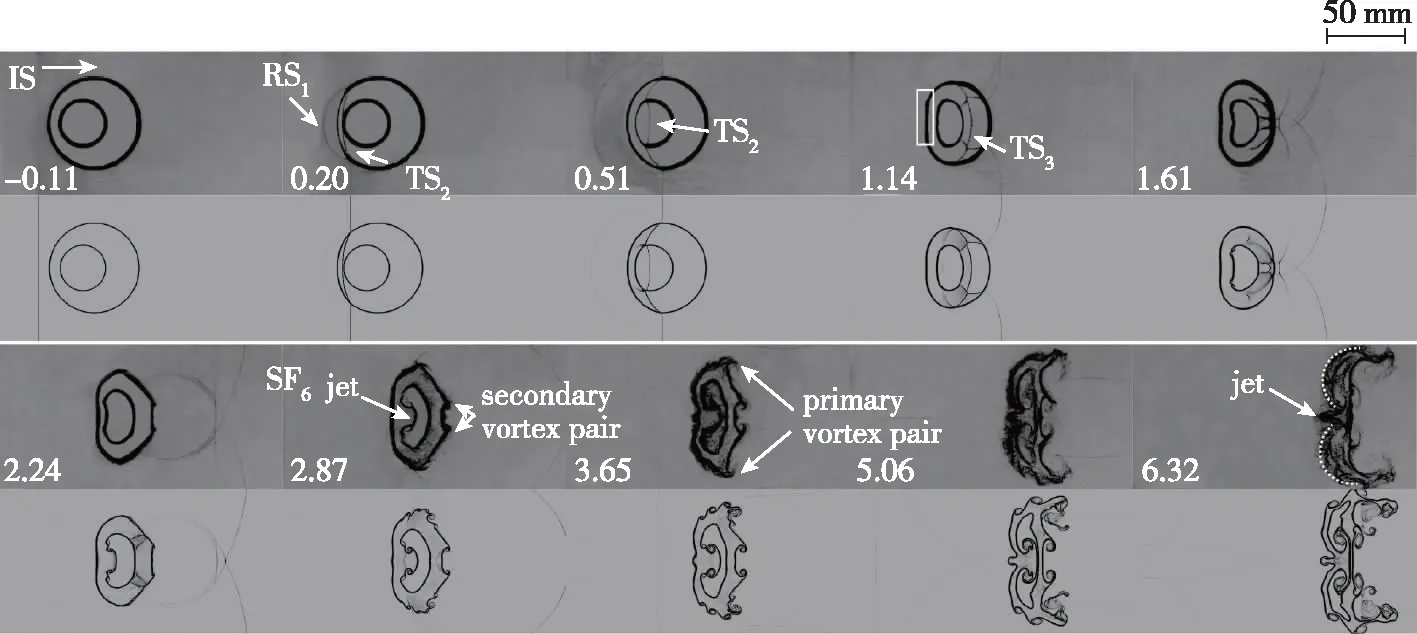
图4 工况I双层SF6气柱被平面激波冲击后实验与数值的纹影图
当TS2作用内层气柱下游界面, 产生三次透射激波(third transmitted shock wave, TS3), 在气环内向下游传播并产生三次反射激波(third reflected shock wave, RS3), 在内层气柱内向上游传播. 随着TS1向下游移动, Mach杆逐渐变短, 最终消失, 4道激波重新相交于一点, 如图7(c)所示. 之后, TS1与其他3道激波分离, 四波点变为三波点, 如图7(d)所示. RS2和TS3在外层气柱下游界面折射形成TRS2(transmitted-RS2)和TS4(fourth transmitted shock wave)以及向上游传播的二次反射稀疏波(second reflected rarefaction wave, RW2), 外部的绕射激波(diffracted shock wave, DS)在下游极点相互碰撞. 最后, TS4和TRS2在界面外部相互作用, TS1和K在界面内部相互作用, 导致外层气柱下游界面附近的压力场十分复杂.
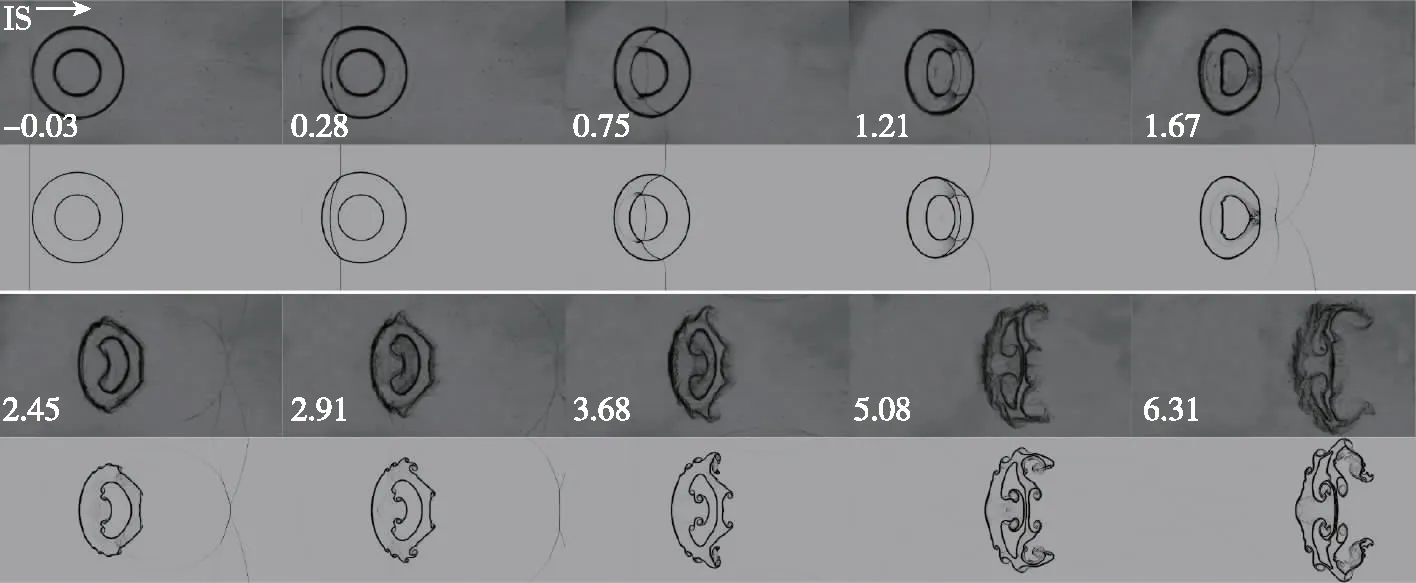
图5 工况Ⅱ双层SF6气柱被平面激波冲击后实验与数值的纹影图
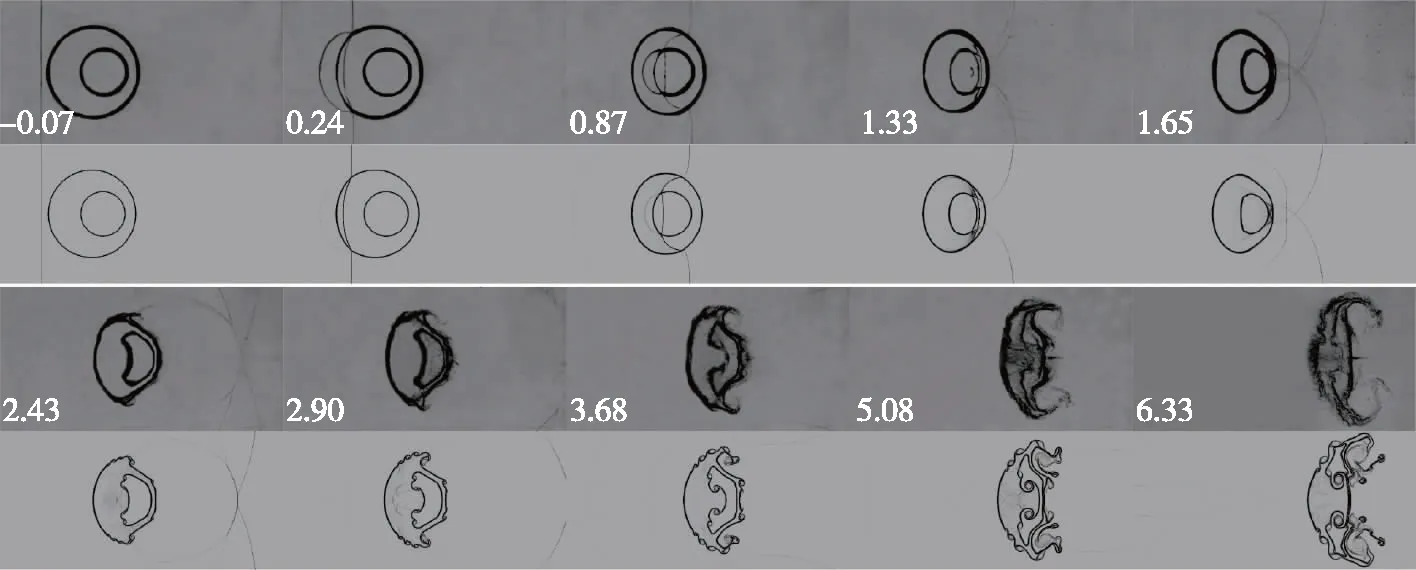
图6 工况Ⅲ双层SF6气柱被平面激波冲击后实验与数值的纹影图
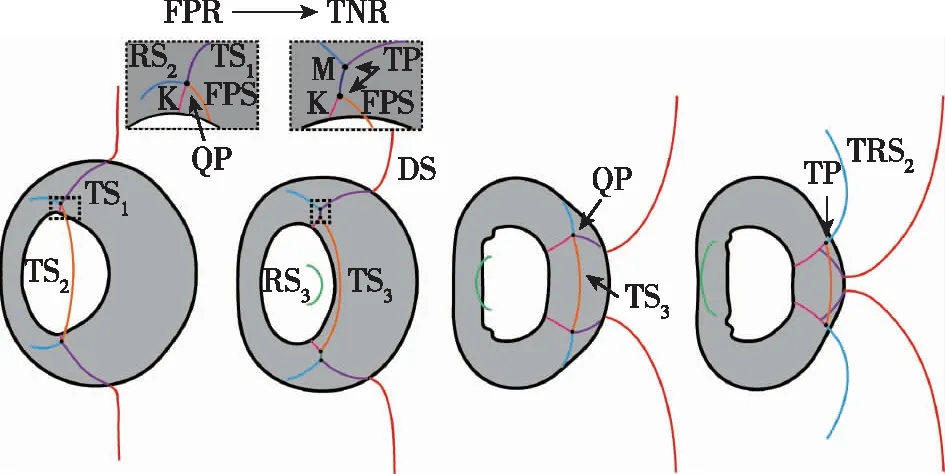
(a) τ=0.67 (b) τ=0.91 (c) τ=1.30 (d) τ=1.45
双层气柱被激波冲击后的早期(τ=0~2.24), 内、 外层界面独立发展, 外层气柱与单层重气柱的演化类似, 气柱被压缩, 上下极值处发展为主涡对; 而内层气柱与单层轻气柱的演化类似, 上游界面会经历反相过程, 形成“SF6射流”. 当三波点碰撞外层气柱下游界面时, 三波点连接的三道激波与界面相互作用, 在沉积涡量的诱导下, 产生次级涡对(τ=2.87), 这与单层气柱的演化有着明显差异[20,43]. 内层气柱发展为涡对, 涡对之间的连接逐渐变细, 由于内层气柱在流向发展时受到外层气柱的限制, 内层气柱被压缩成“细长”结构(τ=3.65).演化后期, 内涡对与外涡对耦合在一起, 外层气柱的主涡对也进一步发展(τ=5.06~6.32).对比实验与数值结果发现, 数值结果很好地复现了流场结构.
当改变内层气柱的位置时, 波系结构与界面演化过程类似, 但仍存在差异. 在内层气柱向上游偏移的工况中, 外层气柱上游界面在激波作用后变成“扁平”状(τ=1.14); 后期, 外层气柱上游界面中心附近凹陷, 界面发展为两个“弓形”且在中心处产生一个向上游的“射流”, 这可能是上游两层界面距离较近, 激波在界面之间来回反射形成的复杂压力场导致的. 在内层气柱靠近下游的工况中, 波系在气柱内演化时, 只出现FPR波系结构, 而未出现TNR 波系结构. 因为内层气柱靠近下游时, TS1接触内层气柱较晚, 而下游两道界面间距较小, 第1次形成四波点后还未来得及产生Mach杆, TS1就已经与其他激波分离, 导致TNR未出现. 此外, 由于下游的两层界面距离较近, 耦合作用发生较早, 两道界面很早就融合在一起(τ=2.90).随着内层气柱位置的改变, 内层气柱的形态在演化后期有明显差异.
2.2 上游极点的位移
为探究受激波冲击后气柱的运动情况, 图8展示了外层气柱上游极点的位移随时间变化情况, 采用外层气柱直径D0对位移进行无量纲. 当入射激波作用外层气柱, 气柱的上游界面获得一定的初速度并向下游运动, 首先经历一个短暂的线性期, 通过拟合实验数据得到不同情况下的线性速度Vi, 如表2所示. 这里的线性速度可以分为3部分速度的叠加: 第1部分是激波冲击后界面获得的阶跃速度ΔV, 可以通过一维气体动力学计算得出; 第2部分是激波在外层气柱上游界面诱导的RM不稳定性的增长率VRM, 可以通过冲击模型[1]计算得到
VRM=akA+ΔV
其中,a和k分别为振幅和波数, 在气柱中分别取a=R和k=1/R(波长λ=2πR), 故ak=1.A+为波后Atwood数. 考虑到激波的压缩效应, 引入压缩因子Zc=1-ΔV/Wi; 此外, 考虑到气柱的波长振幅比(a/λ=R/2(πR)≈0.16>0.1) 不满足小振幅条件, 根据Rikanati理论[47]引入大振幅修正因子φ(在本文中φ=0.828), 有
VRM=φZcA+ΔV
第3部分则是压力等其他因素造成的, 用V0表示, 将线性速度拟合值减去前两部分速度得出. 3部分速度在表2中给出, 其中V0为正值, 表示其方向与入射激波方向相同, 说明压力等因素促进了外层气柱上游界面的运动. 而不同工况下的V0不同, 表明压力幅值与偏心程度有密切关系.Vi表示用实验值拟合的线性速度, ΔV表示由一维气体动力学计算的界面阶跃速度,VRM表示由冲击模型计算的RM不稳定性引起的速度, 表中速度的单位为m·s-1.
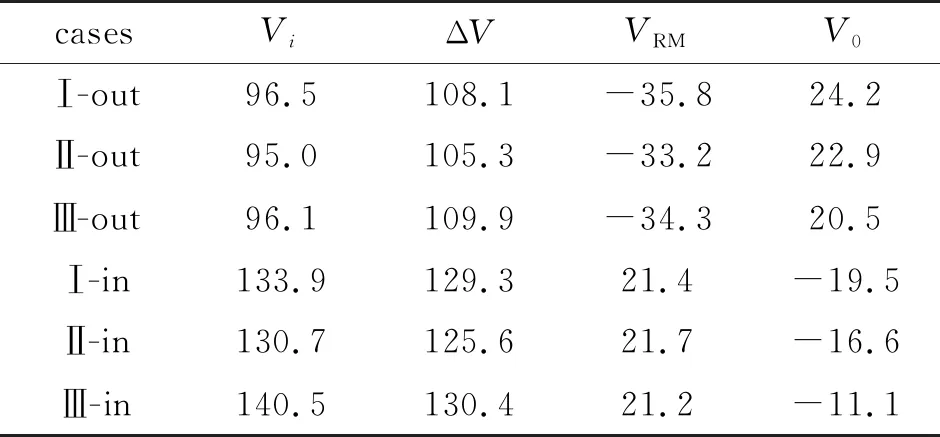
表2 内、 外层气柱上游极点的速度
由于内层气柱上游界面为重/轻界面, 与一次透射激波TS1相互作用后会产生反射稀疏波RW1, 稀疏波向上游传播会加速外层气柱上游界面运动, 使界面很快进入非线性阶段. 图8中的竖直虚线及数字表示RW1作用外层气柱上游界面的时刻. 工况Ⅰ中内层气柱向上游偏移, 上游两道界面间距小, 会最早产生RW1加速外层上游界面, 所以工况Ⅰ的线性期最短, 位移很快大于其他两个工况; 工况Ⅱ 虽然会比工况Ⅲ较早产生RW1, 但是工况Ⅱ 中内、 外气柱上游界面间距小于工况Ⅲ, 内层气柱对外层气柱的抑制作用更早, 在这两个因素的综合影响下, 工况Ⅱ和工况Ⅲ的位移在前、 中期保持一致. 在τ=3.1左右时, 受到从外层气柱下游界面反射的稀疏波RW2作用, 外层气柱上游界面经历第2次加速. 此外, 当稀疏波与外层气柱上游界面作用后会产生向下游传播的反射压缩波, 压缩波在内层气柱上游界面反射产生的稀疏波会再次加速外层气柱上游界面. 这个过程不断重复, 但由于来回反射的波强度逐渐减弱, 界面的加速度逐渐减小. 在τ=5.5左右, 工况Ⅲ的位移超过工况Ⅱ, 但小于工况Ⅰ. 最终, 内外层气柱同心时, 外层气柱上游极点位移最小, 内层气柱向上游偏移时, 外层气柱上游极点位移最大. 说明内层气柱偏心对外层气柱的位移有一定的促进作用, 特别是当内层气柱靠近上游时促进作用更明显. 这一结论与激波作用于含泡液滴[44]时, 内层气泡偏心会抑制外层液滴位移的结论正好相反.
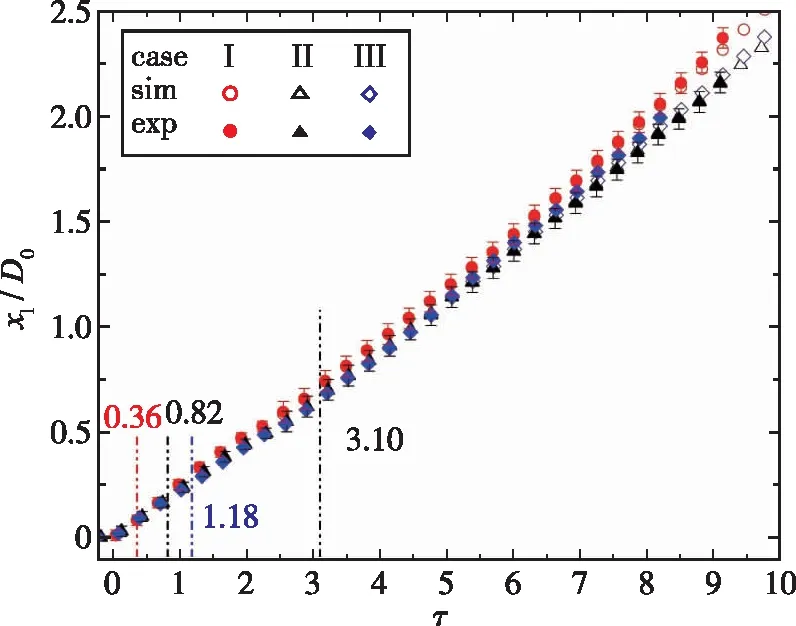
图8 外层气柱上游极点的位移
图9为内层气柱上游极点的位移随时间变化情况, 采用内层气柱直径d0对位移进行无量纲化, 无量纲时间τ′=tWTS/d0, 这里的WTS是一次透射激波TS1的速度,τ′=0对应TS1作用于内层气柱的时刻. 激波作用后, 内层气柱同样先经历了线性阶段. 与外层气柱类似, 实验的线性速度也可以分解为3部分, 如表2所示. 可以发现,V0的方向与入射激波方向相反, 说明压力等因素抑制了内层气柱上游界面的运动.
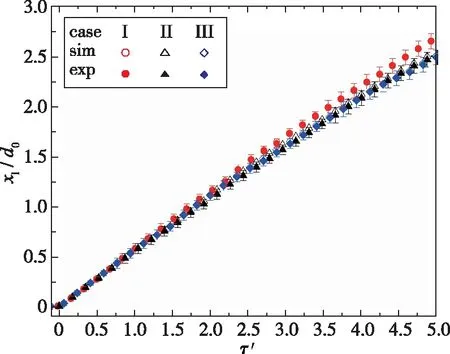
图9 内层气柱上游极点的位移
线性阶段结束后, 由于气柱内部激波反复作用, 界面速度逐渐减小. 初期, 3种工况的位移近似相同, 但在τ′=1.2以后, 工况Ⅰ的位移逐渐大于其他工况, 因为在工况Ⅰ中, 上游两道界面距离很近, 外层界面向下游运动时会促进内层界面运动, 导致界面位移大于其他工况. 由此可见, 内层气柱向上游偏移时, 内、 外层气柱上游极点的位移相互促进.
2.3 气柱宽度与高度
为了探究内层气柱位置对外层气柱演化的影响, 图10展示了外层气柱宽度与高度变化情况. 采用外层气柱的初始宽度W0和高度H0进行无量纲化. 在早期, 外层气柱受到激波压缩宽度减小, 此时, 3种工况有着相同的变化趋势. 但是由于工况Ⅰ的气柱被激波冲击后, 外层气柱上游界面变得“扁平”, 所以气柱宽度减小的速度大于其他情况, 而且宽度被压缩到最窄. 中期, 产生了次级涡对, 主涡对也进一步发展, 气柱宽度略微增大. 后期, 气柱宽度再次减小. 工况Ⅰ中, 外层气柱上游界面产生了“射流”, 随着“射流”不断发展, 气柱宽度在后期逐渐增大, 并最终大于其他情况. 工况Ⅱ与工况Ⅲ在早期变化相同, 但从τ=1.50开始, 工况Ⅲ 的宽度大于工况Ⅱ, 因为工况Ⅲ的内层气柱靠近下游, 内层气柱在发展时下游界面很快与外层气柱的下游界面耦合, 促进外层气柱下游界面向下游运动. 总体来说, 偏心效应会促进外层气柱宽度的发展.
第三,战略利益分配的不公是合作过程中的潜在冲突或成本。一旦出现该冲突或发生此项成本,将直接损害企业参与的积极性。因此,为了实现核心企业与其他联动企业之间的战略协同,必须构建公平合理的利益分配机制,建立利益激励与约束机制,通过合理的奖励制约控制各企业利益诉求。
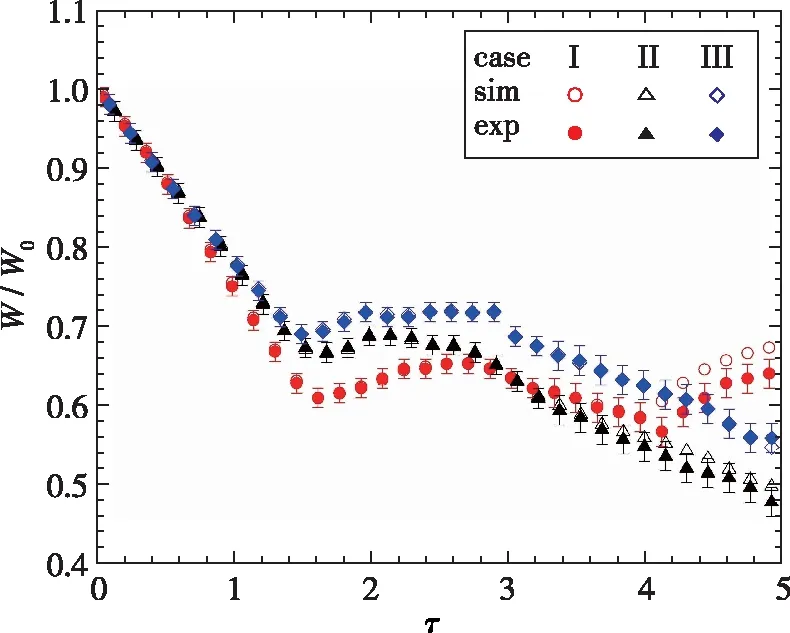
(a) Width
在激波与气柱作用早期, 外层气柱高度保持不变. 当入射激波穿过界面最高点后, 入射激波发展为绕射激波, 使得气柱在展向上被压缩, 高度开始减小. 随着主涡对的发展, 气柱高度逐渐增大. 3种情况下, 外层气柱高度变化在早期类似, 因为早期内层气柱在展向上有足够发展空间, 对外层气柱高度的变化没有影响; 从τ=1.20开始, 工况Ⅰ的高度逐渐大于其他情况, 从τ=2.60开始, 工况Ⅱ的高度逐渐大于工况Ⅲ. 因此, 内层气柱越靠近下游, 外层气柱高度越小, 主要是因为界面耦合并没有对外层气柱的极值点产生明显促进作用, 从而对外层气柱总体高度变化贡献较小.
图11为内层气柱宽度与高度变化情况, 图中无量纲时间定义与图9相同, 宽度和高度采用内层气柱的初始宽度w0和高度h0进行无量纲化. 内层气柱受到透射激波作用后, 宽度急剧减小. 内层气柱越靠近上游, 宽度下降越明显, 这是因为外层界面向下游运动, 挤压内层上游界面, 使得宽度下降更多. 压缩阶段结束后, 下游界面的快速发展导致内层气柱宽度增大. 随后内层气柱上游界面形成的“横向射流”头部与内层气柱下游界面重合, 射流不能穿破界面继续发展, 气柱流向的发展受到了抑制, 导致宽度持续减小. 需要注意的是, 在激波压缩阶段之后, 界面宽度都经历了一个震荡过程, 且内层界面越靠近上游, 震荡周期和宽度变化幅度越明显, 这与气层内部的波系结构往返运动以及界面耦合有一定关系. 3种情况下内层气柱的高度变化情况类似, 只是在早期当内层气柱高度开始减小时, 越靠近下游的气柱由于受到外层气柱的约束, 其高度减小越快. 在中后期, 内层气柱的位置对高度发展影响很小.
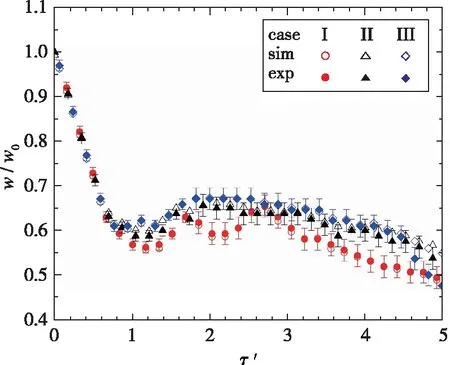
(a) Width
2.4 物质混合与环量
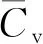
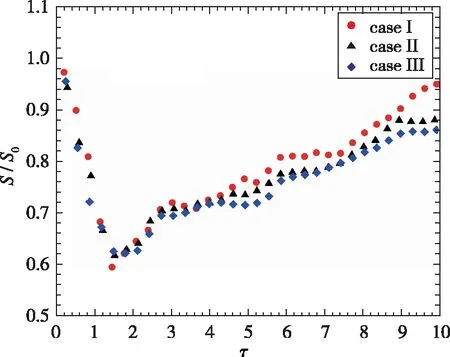
(a) Total interfacial area
其中,Cv表示气柱内各网格点上SF6的体积分数[11,45].
从图12中可以看出, 在激波与气柱作用早期, 气柱受到激波压缩, 面积逐渐减小, 在τ=1.6左右时达到最小值. 主激波离开界面后, 在沉积涡量的诱导下, 内层气柱形成横向射流, 外层气柱形成主涡对和次级涡对并不断发展, 导致内外层气柱界面拉伸或扭曲, 双层气柱的面积逐渐增大. 当内层气柱位置不同时, 气柱面积的变化规律类似, 但工况Ⅰ 的最小值小于另外两个工况, 因为当内层气柱靠近上游时, 稀疏波最早加速外层气柱上游界面, 使得上游界面更靠近下游, 气柱面积更小; 在后期, 内层气柱越靠近下游, 气柱的总面积越小, 在同一时刻, 工况Ⅰ的总面积明显大于另外两个工况, 因为外层气柱的上游界面在后期产生了向上游的射流, 导致气柱面积更大. 当激波冲击气柱后, 气柱内的SF6浓度逐渐降低. 早期3种情况下气体浓度变化相似, 从τ=3.6开始, 工况Ⅰ的平均浓度小于其他工况, 此时向上游的射流开始形成, 气柱的总面积增大, 使得平均浓度小于其他情况. 因此, 当内层气柱向上游偏移时, 会促进双层气柱的物质混合.
界面扭曲导致的物质混合是在涡量的诱导下发生的, 所以有必要对界面上沉积的涡量进行分析. 本文对双层气柱上半平面的涡量进行积分, 得出环量随时间的变化情况, 环量Γ的计算公式如下
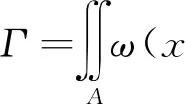
其中,A为上半平面计算区域的面积,ω为界面各网格点上的涡量.

图13 3种工况下中心线上方界面沉积的正环量、 负环量和总环量随时间的变化情况
从图13可以看出, 在达到最大值之前, 正、 负环量均呈线性增加, 而且负涡量主要集中在外层界面, 正涡量主要集中在内层界面, 所以考虑分别计算内、 外层气柱的环量, 然后进行线性叠加[42]获得总环量. 也就是把激波冲击双层气柱获得的环量Γ分解为两部分: 一部分是入射激波IS冲击外层气柱获得的环量Γout, 另一部分是透射激波TS1冲击内层气柱获得的环量Γin, 有
Γ=Γout+Γin
在已有的环量预测模型中, PB模型[8]适用于轻、 重气柱, YKZ模型[48]适用于轻气柱而SZ模型[49]对重气柱预测效果较好. 各种环量模型的表达式如下
其中,R为气柱半径,Vflow为波后流场速度,ρc为气柱内实验气体的密度,ρ0为环境气体的密度.
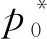

其中,γ=(γ0+γc)/2表示环境气体比热比γ0与实验气体比热比γc的平均值,Mai为入射激波Mach数,c0为环境气体的声速.
本文采用SZ模型和PB模型计算入射激波IS冲击外层气柱获得的环量(环境气体为空气, 实验气体为SF6); 用PB模型和YKZ模型计算透射激波TS1(这里TS1认为是平面激波)冲击内层气柱获得的环量(环境气体为SF6, 实验气体为空气), 并将获得的4个环量值进行两两组合线性叠加, 得到双层气柱的总环量. 在计算环量时, 已经考虑了气体污染带来的影响. 表3给出了数值模拟的环量值和4种环量理论预测值, 结果表明, 用SZ模型计算外层气柱结合PB模型计算内层气柱具有很好的预测效果, 相对误差在1%以内.

表3 各组工况数值结果的环量值(Γsim)与4种组合模型的环量预测值(环量的单位为m2/s)
3 结论
本文采用数值与实验方法研究了平面激波诱导下双层气柱的演化过程, 重点考察了双层气柱的偏心效应对流场演化的影响. 实验中采用肥皂膜技术生成了初始条件可控的双层气柱, 结合纹影技术和高速相机获得了激波冲击后的流场图像. 数值结果与实验结果获得了很好的一致性, 并补充了更多的流场信息.
本文详细描述了双层气柱界面的演化过程和内部的波系结构, 发现随着内层气柱位置的改变, 内、 外层气柱表现出不同的演化特征, 当内层气柱向上游偏移时, 外层气柱的上游界面在后期会产生向上游的“射流”, 当内层气柱向下游偏移时, 下游两道界面会很快融合在一起. 定量分析了内、 外层气柱上游极值点位移的变化情况, 上游极值点首先会经历短暂的线性期. 线性阶段的速度可以分为3部分, 分别为激波冲击后界面获得的阶跃速度、 界面上涡量诱导的速度以及压力等因素导致的速度. 分析发现压力等因素对内、 外层气柱上游界面分别有抑制和促进作用, 而这种促进或抑制作用的大小与内层气柱偏心程度密切相关. 之后由于非线性效应和稀疏波的加速, 界面位移进入非线性阶段. 偏心程度的不同会导致稀疏波加速界面的时间不同, 从而导致界面运动的非线性阶段提前或延迟出现. 对气柱高度和宽度的定量研究表明, 当内层气柱偏心时, 对外层气柱的宽度有着促进作用, 当内层气柱越靠近下游时, 外层气柱高度越小; 内层气柱宽度在向上游偏移的情况中被抑制, 但内层气柱高度并没有明显改变.
最后, 对气柱内部的面积和平均浓度进行了定量分析. 当内层气柱靠近上游, 有着更大的混合面积, 而且气柱内的平均浓度最小, 说明内层气柱向上游偏移会促进物质混合. 最后提取了数值结果中气柱的环量随时间的变化情况, 并用几种经典的环量模型分别计算内、 外层气柱的环量, 最后线性叠加得到总环量的预测值. 结果表明, 用SZ模型计算外层气柱环量叠加PB模型计算内层气柱环量对数值结果具有较好的预测效果.

