一种准二维柱面爆炸波加载装置的设计与验证

刘 澜, 薛 琨, 史晓亮, 李建平

(北京理工大学机电学院, 北京 100081)

引言

将冲击波作为一种加载能源已成为冲击波技术的重要应用方向, 常用于研究材料的结构和物理化学性质变化, 如颗粒、 粉体材料的动态压实[1]、 固态相变[2-3]、 化合物分解[4]、 新化合物的生成[5]等. 目前, 冲击波的生成大部分是利用炸药、 可燃气体爆炸或压缩气体膨胀作为能量源. 常用的冲击波加载装置有激波管、 爆轰激波管、 轻气炮、 高速飞片、 激光冲击等, 这些装置利用高压气体膨胀产生冲击波, 或利用爆轰产物直接或间接撞击样品, 在样品内部产生冲击波. 这些冲击波具有不同的特征波形和特征时间, 已广泛用于研究材料高压状态下的材料特性[6-7]、 冲击波衰减规律[8]、 界面不稳定性[9-10]等问题.

实验室条件下获得的可控冲击波基本为一维传播的平面波, 很难实现汇聚或发散冲击波. 惯性约束核聚变[11]、 体外激波碎石机[12]、 激波聚焦点火[13]等研究领域都涉及汇聚激波. 而发散冲击波普遍存在于各种外爆应用中, 与爆破工程和防护工程密切相关. 目前, 龙桐等[14]和丁举春等[15]采用平面汇聚等装置已经在实验室条件下实现了可控的冲击波汇聚, 但发散冲击波主要依靠炸药爆炸获得, 通过调节炸药种类和距离爆点的等效距离来获得不同超压和冲量的球面/柱面波. 在爆轰产物影响区内爆炸波的波形和稳定性受到膨胀产物气体流动稳定性的强烈影响, 而影响区外的球面/柱面爆炸波曲率半径较大, 且容易受到壁面(如地面)反射波的影响. 在采用炸药爆炸实现发散冲击加载的研究中, 往往利用局部爆炸波对材料/结构进行近似平面的加载, 而非利用完整的球面/柱面波对样品实现径向加载. 炸药的爆压和爆热决定了炸药爆炸后冲击波的超压和冲量. 因此要在同样的曲率半径下改变球面/柱面冲击波超压和冲量, 必须调整炸药的化学组分或者微结构, 这在实际应用过程中是很难实现的. Rodriguez等[16-17]， Grady[18]和Gregoire等[19]设计了由激波管与水平径向Hele-Shaw Cell结合的实验装置, 通过调节激波管内高压段的压力和长度, 可以实现对Hele-Shaw Cell中冲击波超压和冲量的调控. 这种设计实现了在实验室条件下形成可控的发散冲击波. 同时由于Hele-Shaw Cell的准二维特性, 材料在准二维柱面波加载作用下的运动和变形满足平面应变条件. 如果Hele-Shaw Cell的顶板采用透明材质, 则易于采用DIC或PICD等数字图像技术获得测试样品在发散冲击波加载作用下的变形和应变场.

为了将Hele-Shaw Cell内部的柱面冲击波冲击超压提高一个量级, 本文用爆炸管道代替激波管, 用爆炸波驱动Hele-Shaw Cell内部的柱面冲击波. 采用单位当量比的甲烷氧气预混气作为燃爆体系, 获得的冲击波超压可达到3 000 kPa, Mach数可达到2.9. CFD数值模拟揭示了不同结构参数和初始体系条件下燃爆过程的转变, Hele-Shaw Cell内部的柱面波传播过程与燃爆过程的耦合.

1 加载装置设计原理和结构

发散冲击波加载装置原理如图1所示, 其主体部分由充满预混气体的竖直爆炸管道和水平Hele-Shaw Cell组成, 爆炸管道上端出口和Hele-Shaw Cell下板开孔连接, 之间由一层具有一定强度的膜片隔开. 爆炸管道中的预混气体从底部点火后形成竖直向上传播的冲击波, 传播至膜片处后如果无法破裂膜片, 将会向下反射进一步压缩加热预混气, 反射波与火焰面作用后使得火焰面加速. 加速的火焰面诱导出更强的冲击波. 当膜前能量累积到一定值时, 膜片破裂, 高温高压的产物气体释放出强冲击波进入Hele-Shaw Cell内部. 由于Hele-Shaw Cell上下两板的限制, 冲击波从中心孔沿径向向外传播, 形成柱面波. 柱面波的峰值超压、 波形和衰减规律与破膜冲击波压力以及波后产物气体的压力、 温度、 密度密切相关.

图1 冲击波加载装置原理图

基于以上燃爆驱动发散柱面冲击波的设计原理, 设计搭建了如图2所示的实验装置. 爆炸管道主体为长400 mm, 内径30 mm, 壁厚6 mm的钢管, 侧壁处安装开口阀, 用于抽真空和充入预混气体, 底端与电火花点火装置连接. 爆炸管道上端开口处通过法兰和4个螺栓与Hele-Shaw Cell的底板(直径500 mm, 厚8 mm圆形钢板)中部的开孔(直径30 mm)紧密连接, 开口与开孔之间有一片0.1mm 厚的BOPP膜(承压1 MPa). Hele-Shaw Cell上板同样为直径500 mm、 厚8 mm的圆形钢板, 为了便于观测, 将上板的1/4圆面积替换为厚8 mm 的亚克力玻璃板, 玻璃板下表面与其余3/4圆的钢板下表面齐平, 玻璃观测窗与钢板之间的连接如图3所示. 上板通过沿外缘的8个G型夹与下板固定, 通过调节G型夹上下夹头的距离可以调整上下板间隙, 并保证上下板平行, 本实验中保持上下板间隙b=3 mm. 为了获得Hele-Shaw Cell内部压力的演化情况, 在上板3/4圆的钢板上沿相互垂直的两个径向方向L1和L2布设两路压力传感器(Kistler压电式压力传感器), L1方向上传感器距中心的径向距离分别为20, 27.5, 40, 56, 60, 80, 100 mm, L2方向上传感器的径向距离分别为20, 27.5, 40， 56 mm, 如图4所示. 在观察窗上方假设高速摄影机(Photron SA-Z), 用于观测Hele-Shaw Cell内部燃爆产物气体的膨胀运动过程.

图2 装置示意图

图3 装置实物图

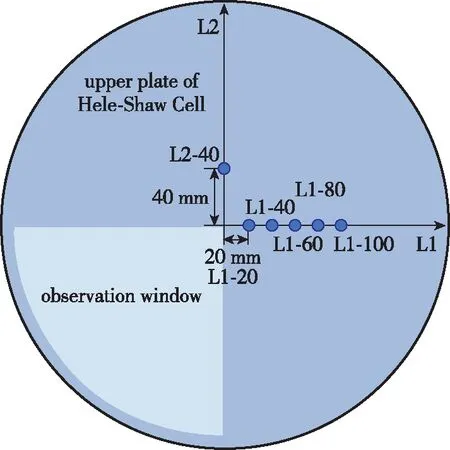
图4 压力监测点分布示意图

2 实验数据分析

实验开始前向爆炸管道内充入已在混气室内混合均匀的单位当量比的甲烷氧气匀混气, 直到管内压力达到设定的预混气初始压力p0.压力测试系统和高速摄像系统通过同步触发实现数据的同步采集. 图5为预混气初始压力p0=0.1 MPa, Hele-Shaw Cell 上下板间距b=3 mm时, 预混气点燃后与高速摄影同步的压力传感器获得的典型压力曲线. 各个位置处的压力曲线都表现出冲击波的特征压力脉冲, 压力上升速率100 kPa/μs, 脉冲宽度为120 μs.

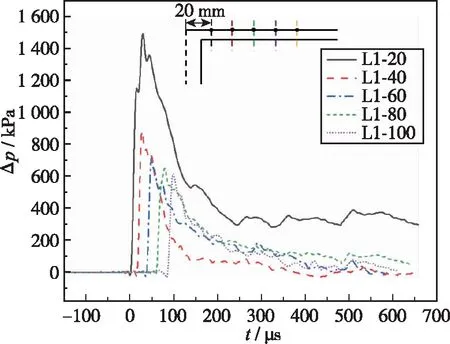
图5 Hele-Shaw Cell内的压力曲线

图6为距离Hele-Shaw Cell中心点相同半径处的不同角度位置处的压力曲线, 可以看出相同半径处压力测点的起跳时间基本重合, 且超压值与超压持续时间都基本相同, 证明了Hele-Shaw Cell内部柱面冲击波的环向均匀性.

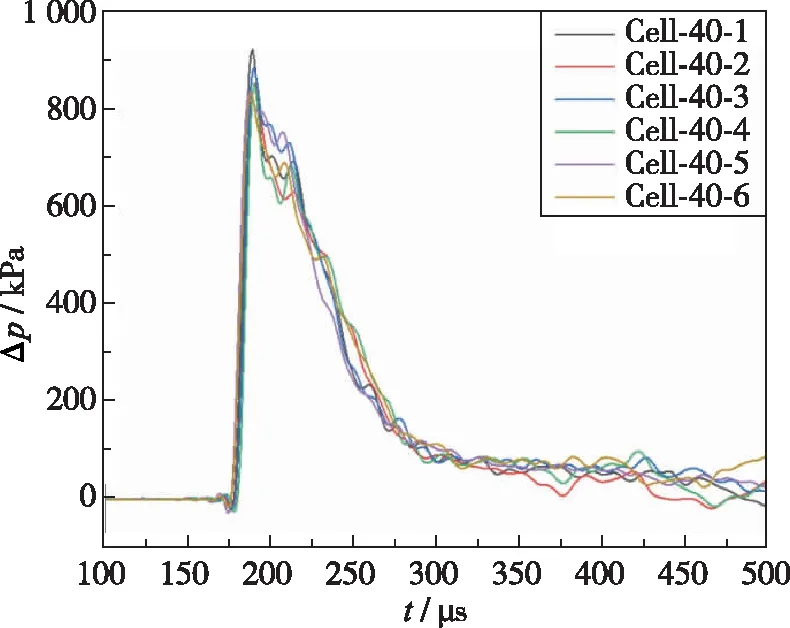
图6 Hele-Shaw Cell内相同半径不同角度处的压力曲线

图7给出了在0.8 ms内Hele-Shaw Cell内部产物气体的膨胀过程. 在最开始的0.15 ms内, 发散出明亮黄白光的高温团状产物气体沿径向膨胀. 通过提取高速摄影图片中高温产物气体的外界面, 分析得到其膨胀速度为700 m/s, 其中, 热扩散不稳定性和气动不稳定性造成了圆形界面的锯齿状微小扰动; 之后产物的膨胀速度明显放缓, 0.2 ms以后膨胀速度仅为300 m/s, 界面扰动的增强和内部流场的湍流加剧了热扩散, 高温产物气体的温度下降表现为辐射光线亮度明显削弱, 由明亮的黄白光转变为相对较暗的红白光; 在0.5 ms时, 产物气体突然再次迸发亮白色光线, 同时在靠近气体出口处出现环形间断面. 根据下面的分析可知, 在冲击波冲破出口处膜片时, 在Hele-Shaw Cell上板反射后向下进入爆炸管道内, 在底部反射后向上传播, 经过已破膜的上端出口再次进入到Hele-Shaw Cell内部, 再次压缩加热Hehe-Shaw Cell内部的产物气体, 使其温度显著增加, 辐射出强烈的白色光线. 0.5 ms和0.7 ms的高速摄影图片上出口附近都出现了环形暗色区域, 意味着高温产物气体已经完全从爆炸管道内进入Hele-Shaw Cell内部. 对比图5， 图7可以发现, 压力脉冲的持续时间仅仅在0.12～0.18 ms, 与产物气体膨胀的第1阶段相对应, 此后压力仅在0.4～0.6 ms出现第2个明显减弱的压力峰, 对应于第2次进入Hele-Shaw Cell内部的压缩波. 膨胀产物气体内部压力的显著下降表现为压力曲线的持续衰减, 甚至出现负压; 流动不稳定造成了压力曲线的小幅波动.

图7 Hele-Shaw Cell内部产物气体的膨胀过程

通过压力测点之间的间距和对应压力起跳点之间的时间间隔可以得到冲击波在两个压力测点之间的平均速度vs.图8给出了峰值超压随径向距离的变化. 在最靠近出口的L1-20(距离出口外缘 5 mm)处出现压力峰值的极值Δpmax～3 700 kPa, 这是由于顶板反射波与径向柱面波的汇聚效应. 超压峰值在稍远的位置处(L1-27.5)迅速衰减到 1 500 kPa, 然后沿径向缓慢衰减. 图9为冲击波传播速度随径向的分布图, 冲击波速度从1 500 m/s衰减到 1 300 m/s, 即Ma从4.4衰减到3.8. 由图10可知, 冲击波位于产物气体界面前方, 且冲击波传播速度远远快于产物气体的膨胀速度. 另外, 尽管峰值超压随径向衰减, 但由于压力衰减速率的放缓, 压力脉冲对应的冲量基本不随径向距离变化.

图8 Hele-Shaw Cell内冲击波超压分布

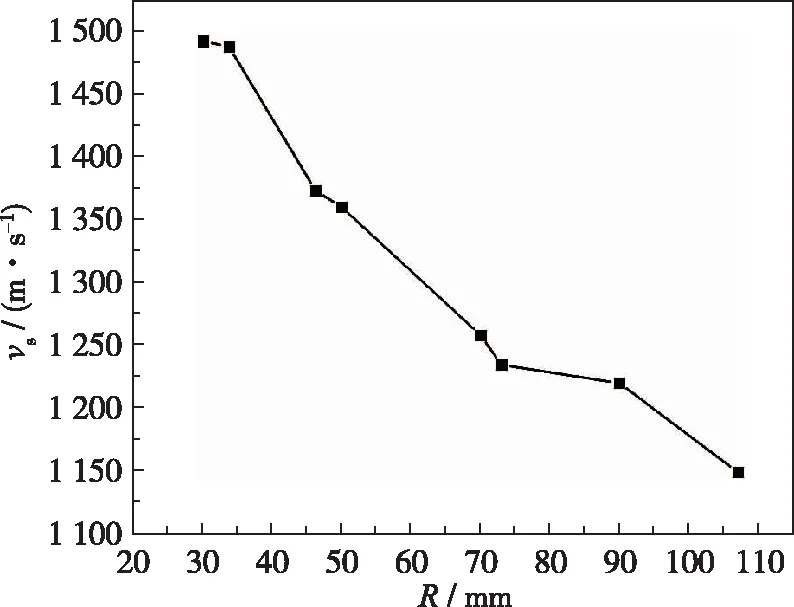
图9 Hele-Shaw Cell内冲击波速度分布

图10 Hele-Shaw Cell内冲击波面与火焰面速度随时间的演化图

3 冲击波产生原理的数值模拟分析

3.1 计算模型

为进一步研究加载装置中冲击波的产生与传播原理, 使用FLUENT软件对燃爆过程以及冲击波的传播过程进行数值模拟. 为了提高计算效率, 在保证计算精度的条件下将实验装置简化为二维轴对称模型. 本文采用 SIMPLE 算法求解压力速度耦合问题, 采用RNG(重整化群)k-ε湍流模型, 使用有限速度模型、 涡耗散燃烧模型求解反应物和生成物输运组分方程, 壁面条件为静态无滑移壁面. 在Gambit中建立模型、 划分网格, 网格尺寸为0.05 mm, 并在近壁面处进行加密. 在爆轰管开口处、 Hele-Shaw Cell内部等距离设置压力监测点, 如图11所示.

图11 计算模型示意图

本文通过改变点火条件来控制爆炸管道内可燃预混气体的燃爆过程, 得到了不同的加载条件.

3.2 爆燃工况

爆炸管道内为初始压力100 kPa的当量比为1的CH4-O2预混气体, 当点火能量为0.2 J, 点火半径为2 mm时, 爆炸管道内实现爆燃过程, 图12为爆燃工况下爆炸管道内的冲击波随时间的传播过程云图. 点火后形成冲击波并向前传播, 对未燃区的预混气体产生压力扰动, 提高了气体的湍流度及温度, 1.05 ms时冲击波第1次到达出口膜片处, 反射后反向向点火端传播, 到达管道中间位置时, 反射波与预混气体进一步燃烧反应产生的压缩波相遇、 叠加, 再次向出口端传播. 期间, 不断产生与反射的冲击波提高了爆炸管道内预混气体的湍流程度, 火焰、 冲击波相互耦合的正反馈机制使得爆炸不断加速[20], 冲击波速度由0.45 ms时的411 m/s增大到1.95 ms时的1 000 m/s, 多个冲击波相互追赶叠加形成强冲击波, 直到2.028 ms时冲击波破膜进入Hele-Shaw Cell中. 此后, 冲击波不断在点火端和上板之间反射, 所以在压力曲线中出现多个峰值.

图12 爆燃工况下冲击波传播过程的压力云图

图13为上述工况下数值模拟中冲击波在爆炸管道内和破膜后在Hele-Shaw Cell内传播过程中的压力曲线图. 在爆燃条件下, 预混气体被点燃后会先形成一系列的压缩波, 并汇聚成一道较强的压缩波在爆炸管道内传播、 反射, 表现为压力曲线图中的第1个较小的波峰, 之后这一系列压力波耦合成一道强冲击波, 表现为爆炸管道出口处压力监测点的较高的波峰, 随后冲击波破膜并进入Hele-Shaw Cell内, 表现为L1方向监测点的压力曲线.

图13 数值模拟中的压力曲线

图14为相同工况下实验中得到的压力曲线图, 通过比较可以看出, 相同工况下, 数值模拟得到的爆炸管道内和Hele-Shaw Cell内的冲击波速度分别为1 200, 1 428 m/s, 而实验得到的分别为1 180, 1 276 m/s; 相同位置测点处的超压值基本吻合, 但数值模拟中在2.5 ms后会出现一个超压值更大的反射波, 而在实验数据中并没有明显的反射波峰, 认为是由于实验装置的粗糙度等因素对超压的衰减效果更为明显.

图14 实验中的压力曲线

3.3 爆轰工况

爆炸管道内为初始压力100 kPa, 当量比为1的CH4-O2预混气体, 当点火能量为20 J, 点火半径为2 mm时, 爆炸管道内实现爆轰过程, 图15为爆轰工况下爆炸管道内的冲击波随时间的传播过程云图. 预混气体点燃后, 直接形成一道强冲击波向膜片处传播, 并随着传播距离的增加逐渐稳定, 当传播至爆炸管道出口处时, 冲击波超压达到2 900 kPa, 速度为2 300 m/s, 符合该初始条件下CJ爆轰的参数.

图15 爆轰工况下冲击波传播过程的压力云图

图16为上述工况下数值模拟中冲击波在爆炸管道内和破膜后在Hele-Shaw Cell内传播过程中的压力曲线图. 可以明显看出, 在爆轰工况下, 爆炸管道内压力监测点表现为一道强冲击波的波峰, 破膜后Hele-Shaw Cell内压力监测点起跳. 图17为相同工况下实验得到的压力曲线图, 通过压力曲线之间的比较可以看出, 相同工况下, 数值模拟得到的爆炸管道内和Hele-Shaw Cell内的冲击波速度分别为2 300, 1 500 m/s, 而实验得到的分别为2 380, 1 306 m/s, 与爆燃工况相比, 爆炸管道内冲击波速度明显增大, 基本符合爆轰理论速度, 但在Hele-Shaw Cell内冲击波速度没有明显增大, 其原因是当爆炸管道出口膜片附近累积了一定程度的能量后, 膜片才会被冲破, 所以爆燃和爆轰工况下破膜后的冲击波能量相近, 且在随后的分析中可以知道, 初始能量越大, Hele-Shaw Cell对冲击波的衰减效果越明显. 相同位置测点处数值模拟与实验得到的超压值相差不大, 但与爆燃工况相似, 数值模拟可以清楚地反映爆炸管道内以及Hele-Shaw Cell内的反射波, 但实验中的衰减则表现得更加明显.

图16 数值模拟中的压力曲线

图17 实验中的压力曲线

另外, 可以明显看出, L1-20点压力曲线的超压值与波形都存在明显的不规律现象, 解释为冲击波由爆炸管道进入Hele-Shaw Cell时, 会在拐角处出现明显的绕射与斜反射现象, 所以在 Hele-Shaw Cell靠近中心点处会存在一个压力不稳定区域, 如图18所示. 冲击波破膜后在上板处发生反射, 反射超压产生很大幅度的增大, 随后大部分反射波回到爆炸管道内向点火端传播, 小部分冲击波通过绕射和斜反射进入Hele-Shaw Cell内, 且在一定范围内呈现不稳定传播, 表现为图19中L1-20测点处压力曲线线形与超压的不规律性, 一直到L1-40点处才转化为沿径向传播的稳定柱面波. 且由云图可以明显看出, 冲击波由于衰减和持续的斜反射, 其在Hele-Shaw Cell内随着传播距离的增加, 高压区域不断增大, 表现为图19中L1-60之后压力测点的平缓下降沿. 因此, 当加载过程中以超压加载为主时, 认为当R≥40 mm时为超压稳定加载区域.

图18 爆轰工况下Hele-Shaw Cell内的压力云图

图19 爆轰工况下Hele-Shaw Cell内不同位置处的压力曲线

4 加载规律研究

4.1 Hele-Shaw Cell内超压分布规律

本节研究了当量比为1的CH4-O2预混气体在爆燃与爆轰两种工况下, Hele-Shaw Cell内部超压的分布、 衰减规律, 并通过改变预混气体的初始压力, 研究其对超压分布规律的影响.

图20为相同预混气体在初始压力为100 kPa时, 数值模拟的爆燃与爆轰两种燃爆工况与实验中的爆燃工况中Hele-Shaw Cell内的超压分布散点图, 并进行函数拟合. 由图20可以明显看出, 爆燃工况下, 在相同位置测点处, 数值模拟得到的超压值略大于实验值, 且由曲线斜率可以看出, 超压衰减速率也略低于实验值, 这是因为爆燃过程本身存在不确定性. 由图20中两种燃爆工况的数值模拟结果可以看出, 初始压力相同时, 爆轰工况下Hele-Shaw Cell 内的超压值要明显大于相同位置处爆燃工况得到的超压值, 由曲线斜率分析也可得到爆轰工况下的超压衰减速率也明显大于爆燃工况, 且在爆轰工况下, 冲击波超压在Hele-Shaw Cell内衰减可达76%, 而爆燃工况则为63%, 可以认为, 初始能量越大, 装置对冲击波的衰减效率越大.

图20 实验与数值模拟中Hele-Shaw Cell内的超压分布

在爆轰工况的数值模拟中, 研究了不同初始压力对Hele-Shaw Cell内超压衰减规律的影响. 图21为爆轰工况下, 初始压力不同时Hele-Shaw Cell内的超压分布散点图和相应的拟合曲线, 由拟合函数可知, 初始压力越大, Hele-Shaw Cell相同位置处的超压值越大, 且当初始压力在小范围内变化时, 超压值在Hele-Shaw Cell内的衰减规律相同, 拟合函数的系数则与初始压力有关, 由此, 得出爆轰工况下Hele-Shaw Cell内任意位置处超压值pi的计算公式

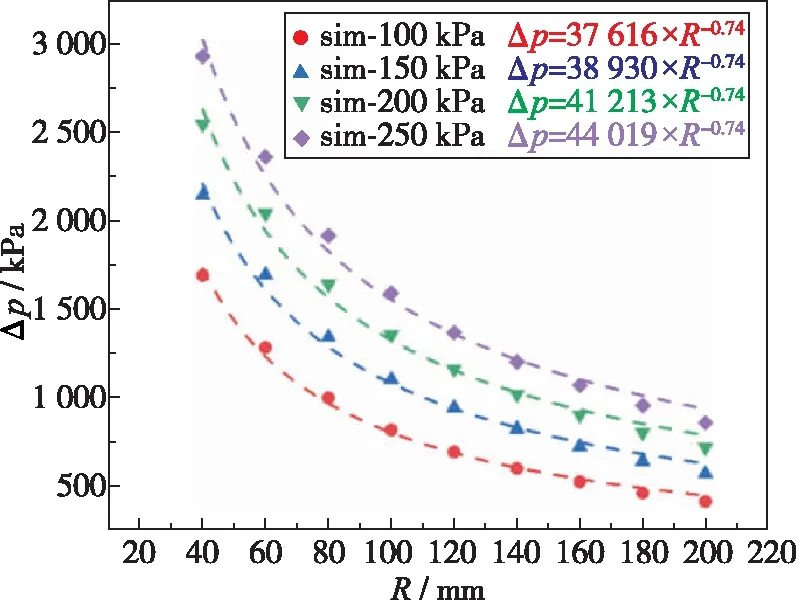
图21 爆轰工况中不同初始压力下Hele-Shaw Cell内的超压分布图

pi=16 757×p00.17×R-0.74

式中,p0为当量比等于1的CH4-O2预混气体的初始压力, 单位为kPa;R为Hele-Shaw Cell中测点与中心点之间的距离, 单位为mm. 上式可以用于此径向冲击波加载装置在爆轰工况的不同初始条件下的超压预测计算.

4.2 Hele-Shaw Cell内冲击波比冲量分布规律

本节研究了数值模拟的爆轰工况中, 不同初始压力下Hele-Shaw Cell中不同位置测点处的冲击波比冲量, 即正压作用区超压对时间的积分值, 如图22所示. 可以看出, 由于冲击波刚进入Hele-Shaw Cell时传播速度高达1 500 m/s, 所以虽然超压值较大, 但比冲量值却较小. 随着冲击波传播距离的增加, 速度不断衰减, 比冲量值开始增大到最大值, 且最大值出现的时间随着初始压力的增大而推迟, 原因为初始压力越大, 冲击波衰减到较低值所用的时间就越长. 比冲量到达最大值后, 开始随着传播距离呈线性衰减, 如图22中的线性拟合曲线所示. 因此, 当加载过程中更加注重比冲量的加载效果时, 可以将加载材料放置在R≥100 mm位置处.

图22 爆轰工况中不同初始压力下Hele-Shaw Cell内冲量分布图

5 结论

本文设计并搭建了一套准二维、 径向发散冲击波加载装置, 通过数值模拟的方法研究了其加载原理, 通过对比实验数据证明了其流场均匀性和加载可靠性, 并通过改变爆炸管道内的燃爆过程和初始压力实现了对加载参数的调节.

结果表明, 当爆炸管道内可燃预混气体的初始压力相同时, 爆炸管道内的燃爆过程对Hele-Shaw Cell内的加载超压有较大的影响, 其中, 在加载区域内, 即R为0～200 mm时, 爆燃工况冲击波超压衰减为63%, 爆轰工况则可达到76%, 衰减速率明显加快, 相同位置测点处的超压值也是爆燃工况的1.7倍; 但爆炸管道内燃爆过程对Hele-Shaw Cell内冲击波速度的影响较小, 在爆炸管道出口处, 爆轰工况得到的冲击波速度约为爆燃工况的2倍, 但冲击波进入Hele-Shaw Cell时速度却都保持在 1 500 m/s.

当燃爆过程相同, 即为稳定爆轰工况时, 初始压力增大后, Hele-Shaw Cell内相同位置测点处的超压值明显增大, 且由函数拟合可知, Hele-Shaw Cell内超压随传播距离的衰减规律相同; 通过数据拟合得到了爆轰工况下Hele-Shaw Cell内任意位置处超压值pi的计算公式, 用于此径向冲击波加载装置在爆轰工况的不同初始条件下的超压预测计算; Hele-Shaw Cell内冲击波比冲量的分布随传播距离的增大先增大再减小, 这一变化规律由冲击波速度的衰减造成.

最后, 此径向冲击波加载装置存在加载不稳定区域, 通过云图和数据分析, 认为, 当爆炸管道内径为15 mm、 Hele-Shaw Cell狭缝宽度为3 mm时, 超压稳定范围为R≥40 mm区域, 比冲量稳定范围为R≥100 mm区域, 不稳定区域范围的大小与初始能量、 装置参数等都有关系.