活跃在2023年高考卷中的“爪形”三角形

安徽省芜湖市第一中学(241000) 刘海涛 张大伟

《普通高中数学课程标准(2017 年版2020 年修订)》(下称《课程标准》)指出[1]:“通过高中数学课程的学习,学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称‘四基’);提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称‘四能’).”梳理2023 年高考数学卷, 有这样一类解三角形问题,连接已知三角的一个顶点与其对边的任一点,构成“爪形”结构的图形,求解该类三角形的边、角、面积等. 这类问题能有效考查学生的直观想象、逻辑推理、数学运算、数据分析等数学核心素养,既有对解三角形基本知识、基本思想方法的考查,也有融合向量、解析几何等知识的考查,体现了高考的基础性、综合性、创新性的考查要求,具体如下表1. 由于解三角形知识的本身特性,近五年的高考中尚未考查其应用性.

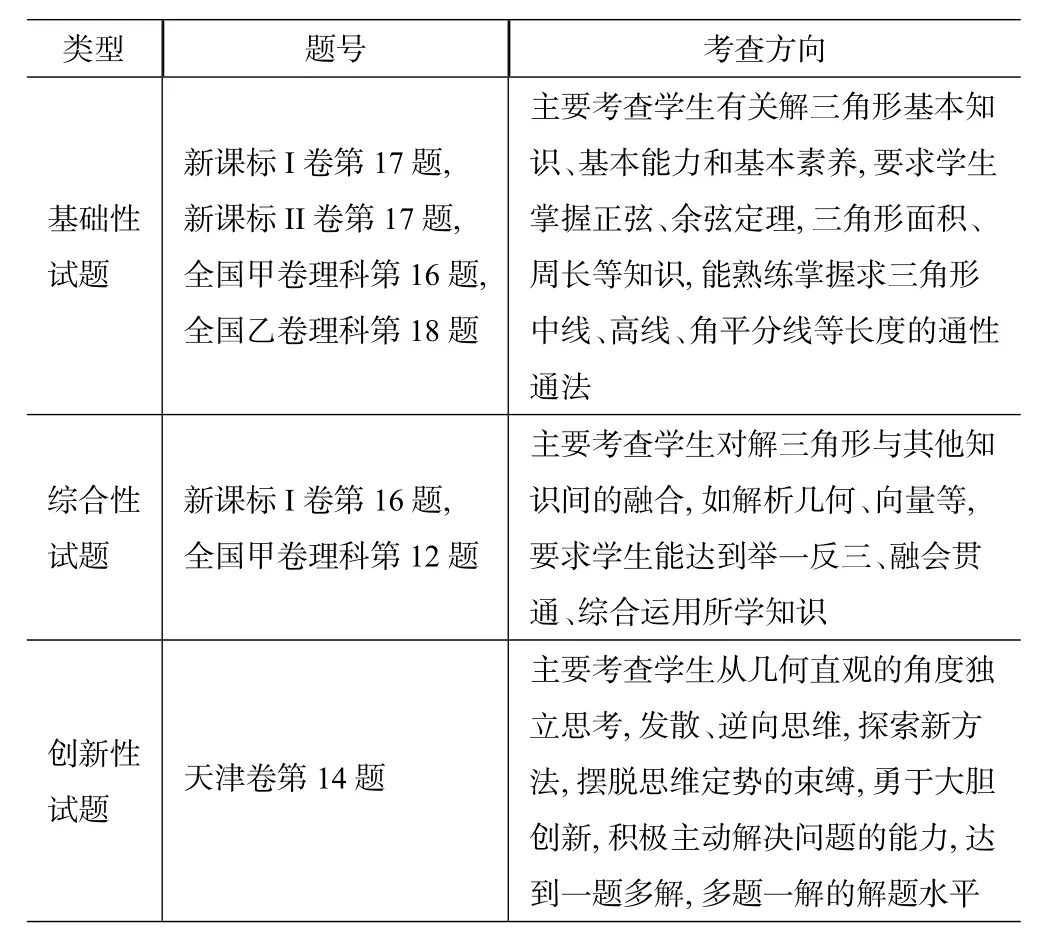
表1: 2023 年高考“爪形”三角形试题分类

1 有关“爪形”三角形的性质

如图1 所示, 在∆ABC中, 角A,B,C的对边分别为a,b,c,D为BC上一点. 则有如下性质:

性质1

性质2(张角定理)

证明由S∆ABD+S∆CBD=S∆ABC,得

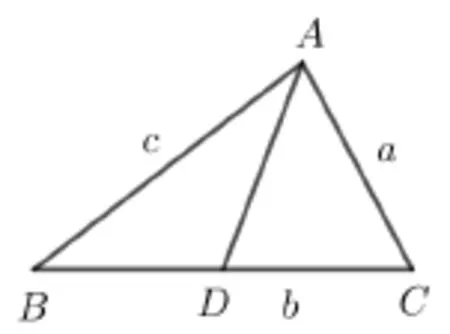
图1

性质3(斯特瓦尔特定理)

证法1在∆ABD和∆CBD中, 由余弦定理, 得c2=AD2+BD2-2AD·BD·cos ∠ADB,a2=CD2+BD2-2CD·BD·cos ∠CDB,注意到∠ADB+∠CDB=π,则

特别地, 当BD为中线时, 有则

当BD为∠ABC的角平分线时, 有得a·AD=c·CD,则

2 部分试题分析

2.1 立足基础,考查通性通法

《中国高考评价体系》指出:高考围绕学科主干内容,加强对基本概念、基本思想的考查,杜绝偏难怪题和繁难试题,引动教学重视教材,夯实学生学习基础,给学生提供深度学习和思考的空间[2]. 2023 年高考“爪形”三角形试题,主要考查学生有关解三角形基本知识、基本思想方法,要求学生掌握正弦、余弦定理,三角形面积、周长等知识,如新课标I 卷第17 题,新课标II 卷17 题,全国甲卷理科第16 题,全国乙卷理科第18 题等,这四道试题均来源于教材的例、习题的改编,只要学生基础扎实,熟练掌握求三角形中线、高线、角平分线等长度的通性通法,考场中便可轻松解题.

例1(新课标全国Ⅱ卷)记∆ABC的内角A,B,C的对边分别为a,b,c,已知∆ABC的面积为D为BC中点,且AD=1.

(2)若b2+c2=8,求b,c.

解析(1) 的解法1 在∆ADC中,得a= 4. 在∆ABD中,由余弦定理, 得cos ∠ADB= 7, 则又因为B为锐角, 所以tanB=

(1) 的解法2 同法1, 得a= 4, 由余弦定理, 得b2=CD2+AD2-2CD·AD·cos ∠ADC=3,得注意到AC2+AD2=DC2,得如√图2 所示,过A作AE⊥BC于点E,于√是则

(2) 在∆ABC中, 由D为BC中点, 且AD= 1, 得由即∠ADC=于是得b=c=2.

评注该题属于中等难度试题,解题的关键在于熟练运用余弦定理、三角形面积公式等处理三角形中的边角关系,对于“爪形”三角形中的中线,能够熟记公式并运用,该题有效考查了学生的直观想象、逻辑推理、数学运算等数学核心素养.

图2

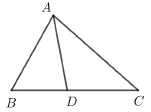
图3

例2(甲卷理科第16 题)在∆ABC中,∠BAC= 60◦,的角平分线交BC于D, 则AD=____.

解法1如图3 所示, 由余弦定理, 得AB2+AC2-由张角定理,得则AD=2.

解法2同法1, 得AC= 1 +3. 由正弦定理,得则在∆ABD中,∠ADB=75◦,所以AD=AB=2.

评注该题作为填空压轴题,有一定难度,对于“爪形”三角形的角平分线问题,既可以利用三角形的面积公式解决角平分线问题,也可以用角平分定义结合正弦定理、余弦定理求解.

2.2 注重综合,考查知识的融会贯通

《中国高考评价体系》指出:素质教育是内涵丰富的全面发展教育. 高考要求学生能够触类旁通、融会贯通,既包括同一层面、横向的交互融合,也包括不同层面之间、纵向的融会贯通[2]. 2023 年的高考数学卷中,新课标I 卷第16 题和全国甲卷理科第12 题分别以双曲线和椭圆为背景考查“爪形”三角形,考查了圆锥曲线的基本几何性质、解三角形等相关知识,需要考生能够将解析几何与三角形等知识融会贯通起来,属于难度较大的综合性试题.

例3(新课标I 卷第16 题)已知双曲线C:1(a,b>0)的左、右焦点分别为F1,F2. 点A在C上,点B在y轴上,则C的离心率为____.

解法1如图4 所示,设B(0,m),由得

则m2= 4c2. 由点A在C上, 得结合b2=c2-a2整理得25c4-50a2c2+9a4=0,得5c2=9a2或5c2=a2(舍),所以

解法2设|BF1|=|BF2|=x, 则即得

评注该题是一道解析几何与解三角形的综合性问题, 关键在于构造出关于a与c的齐次方程式, 注意到|F1F2|= 2c, 且F2为∆F1AB边AB上的一定比分点, 故根据题意用a表示∆F1AB的各边长, 再利用便可轻松解题.

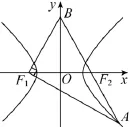
图4

图5

例4 (甲卷理科第12 题) 已设O为坐标原点,F1,F2为椭圆C:的两个焦点, 点P在C上,

解法1如图5 所示, 设P(x0,y0), ∠F1PF2= 2θ. 由所以故选B.

解法2在∆PF1F2中,由余弦定理,得

结合2|PF1||PF2|= (|PF1|+|PF2|)2-|PF1|2-|PF2|2,由O为F1F2中点, 得|OP|2=故选B.

评注该题是压轴选择题,具有一定的综合性,属于中等偏难试题. 该题根据求解的目标可以选择利用椭圆中的二级结论焦点三角形的面积公式快速解出,也可以常规利用定义结合余弦定理,再直接利用“爪形”三角形中线长公式解决.

2.3 强调创新,考查思维的灵活性

《中国高考评价体系》指出: 素质教育中的智育和以往教育理念中的智育最大的不同,在于其对创新性的强调[2].通过命题创新,创设新颖的试题情境、新颖的题目条件、新颖的设问方式,考查考生学生思维的灵活性与创造性. 2023 年高考的天津卷第14 题,虽是“爪形”三角形问题,却没有设问解三角形,而是将问题设置为求向量数量积的最大值,需要考生借助向量来“翻译”题中的各个“爪形”三角形,最终将问题转化为函数的最大值问题,有效考查学生思维的灵活性与创新性.

例5(天津卷第14 题)在∆ABC中,∠A= 60◦,BC=1, 点D为AB的中点, 点E为CD的中点,若设可用a,b表示为____;若则的最大值为____.

解析如图6 所示, 由题知

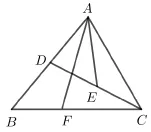
图6

设|a|=p,|b|=q, 则在∆ABC中, 由余弦定理, 得AB2+AC2-BC2=2AB·AC·cosA,即p2+q2=1+pq.由p2+q2≥2pq,得pq≤1(当且仅当p=q= 1 时取等号).由

于是当p=q=1 时取最大值,为

评注该题中共蕴含了三个“爪形”三角形,但题目并未设问求相关长度问题,而是以一个不定三角形为背景,以向量的形式来考查学生对三角形、向量、不等式、函数等知识,属于一道创新性试题,能够有效考查学生的思维的灵活性与创新性.

3 高考备考

高考试题是命题者在《课程标准》和《中国高考评价体系》的指导下, 经过反复酝酿、打磨、斟酌而成, 对高考的备考具有导向性与启示性[3]. 因此,作为一线教师,应该善于从“四层”“四翼”的角度对高考真题予以分类整理,归纳总结出一类试题的通性通法, 使得学生跳出“题海”, 高效备考.2023 年高考一共有九套试卷(全国甲、乙卷的文、理卷,新高考的I、Ⅱ卷,北京卷、上海卷和天津卷),笔者梳理解三角形问题,发现共有7 道试题以“爪形”三角形为背景考查解三角形知识,而通过深入分析这7 道试题,基于“四翼”的角度可以将其归纳为三类,基础性试题、综合性试题、创新性试题,文中分别选取典型试题予以分析,以帮助读者掌握三类试题的解法,提高数学核心素养和解题能力.