双分裂线路短路电流作用下间隔棒载荷特性分析

高英博, 严 波, 刘光辉, 蔡道达, 陶亚光, 刘泽辉

(1. 重庆大学 航空航天学院,重庆 400044;2. 国网河南省电力公司电力科学研究院,郑州 450052)

分裂导线间隔棒在输电线路正常运行情况下起到保持分裂导线的几何形状,限制子导线之间相对运动的作用[1]。当线路发生短路故障时,流经导线的电流迅速增大使分裂子导线间产生较大的电磁力,从而使各分裂子导线相互吸引并对间隔棒产生瞬间冲击作用。发生短路故障时间隔棒承受的载荷是间隔棒设计的重要指标,其准确计算对间隔棒的设计和线路的安全运行具有十分重要的意义。

Manuzio[11]结合理论和试验,最早提出了短路电流作用下分裂导线间隔棒最大向心力计算公式。其假设电磁力作用下子导线吸附过程中张力保持不变,且作用力的大小与档距和档内间隔棒的个数及位置无关。目前,我国间隔棒设计规程[12]中也采用Manuzio提出的公式。欧珠光等[13]等建立了一个档距210 m包含一个相间间隔棒的两相单导线试验系统,测试了不同短路时间和相位差在正常和松弛张力情况下相间间隔棒所受的冲击力。胡建平等[14]利用四分裂间隔棒三维实体有限元模型计算了短路故障时其变形和应力。李升来等[15]建立了四分裂导线-间隔棒有限元模型,计算了短路电流电磁力作用下间隔棒和导线的变形。司学振等[16]利用三维实体有限元模型计算了四分裂导线间隔棒在短路电流作用下的应力。这些工作均采用规程公式计算间隔棒向心力,没有考虑导线运动过程中电磁力变化引起的间隔棒向心力改变,且均仅做了静力分析。

本文针对典型双分裂线路,数值模拟发生短路故障时的电流强度,利用ABAQUS用户自定义程序UEL,实现导线运动过程中子导线电磁力的计算,模拟分裂导线在短路电流作用下的动力响应过程,分析作用于间隔棒上的动力载荷,得到导线运动过程中间隔棒向心力的最大值。进而对短路电流、导线型号、档距、间隔棒排布方式、子导线分裂间距、初始张力、高差和风速等进行参数分析,获得这些参数对间隔棒向心力的影响。本文研究结果对双分裂线路间隔棒的设计和安装具有重要的指导意义。

1 导线动力响应数值模拟方法

为准确计算短路电流下间隔棒向心力的大小,需考虑输电线路发生短路故障后电流的变化和导线运动过程中电磁力的变化。

1.1 输电线路短路电流计算方法

MATLAB中的电力系统模块(power system blockset,PSB)是一种针对电力系统的可视化建模与仿真工具,将SIMULINK和PSB结合使用可实现复杂的、非线性电力系统的建模与仿真。基于MATLAB/SIMULINK仿真的电力系统可表示为线性电路的状态空间模型和非线性元件反馈模型,如图1所示[17]。

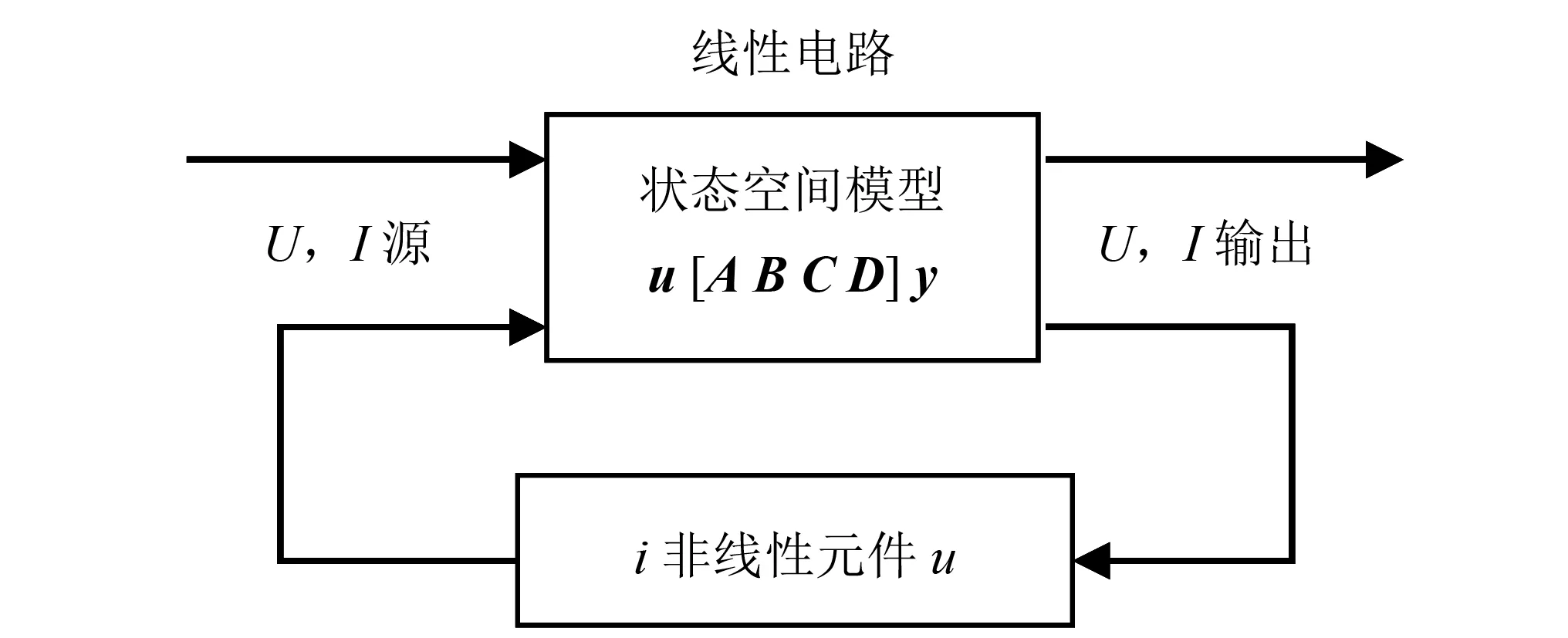
图1 反馈式电力系统状态空间模型Fig.1 State space model of feedback power system

线性电路主要包括电阻、电抗、电容和互耦电感,其状态方程可表示为

x′=Ax+Bu

(1)

y=Cx+Du

(2)

式中:x,x′为状态变量及其导数;u为输入向量;y为输出向量;A,B,C,D为状态矩阵。

在线性电路中,状态变量为电容电压和电感电流,电流源和电压源为输入,测量电流和电压为输出。非线性元件如电机、开关等用非线性U-I曲线来建模。非线性元件用两端的电压u作为输入,并将返回的非线性元件电流i作为注入电流注入线性电路状态空间模型,从而在线性电路状态空间模型输入、输出间形成反馈回路[18]。电力系统短路故障仿真通过三相故障模块的设置使得三相导线相和相之间、相与地之间实现断开与闭合状态的切换,获得不同状态下的电力系统模型,从而计算出电力系统的稳态电流以及发生短路故障时的暂态电流。

1.2 子导线间电磁力计算方法

根据Mehta等提出的计算载流子导线之间电磁力的方法。假设空间上存在任意构型的导线C1和C2,通过其电流方向相同,大小分别为I1和I2,如图2所示。i,j,k分别为笛卡尔坐标系xyz3个方向的单位向量。

图2 载流导线电磁力模型Fig.2 Electromagnetic force model of current-carrying conductors

每根子导线由Nelm个单元离散,则导线C1上的单元p和导线C2上的单元q之间的电磁力为

(3)

式中:μ0为真空磁导率,为4π×10-7H/m;dl1和dl2分别为导线C1和C2的单位长度向量;R为单元p中点到单元q中点的向量;ar为R的单位向量。于是,单元p受到导线C2所吸引产生的电磁力为

(4)

对于任意分裂数Nbnd的分裂导线,子导线上的单元会受到其他子导线吸引而产生电磁力。根据式(3)和式(4)可得,第i根子导线上的单元p受到的电磁力可以表示为

(5)

1.3 电磁力用户自定义程序UEL开发

分裂导线运动过程中,子导线之间的距离不断变化,因而它们之间的电磁力也会变化,即电磁力的大小与导线当前运动状态有关。故利用ABAQUS软件中用户自定义子程序UEL定义了一个无质量、无刚度的单元,该单元与离散子导线的梁单元共结点,因此可通过子程序获取子导线所有结点在任意时刻的位置,进而实现电磁力的计算。

ABAQUS隐式积分采用Hilber-Hughes-Taylor方法,其动态平衡方程与余量方程分别由下式表示

(6)

(7)

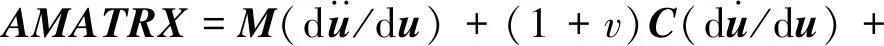
(8)

(9)

AMATRX=0

(10)

RHS=(1+v)Gt+Δt-vGt

(11)

此处Gt+Δt和Gt分别按照1.2节计算得到的t+Δt时刻与t时刻的电磁力。由于自定义单元与离散导线的梁单元共结点,故通过式(11)即可将电磁力施加到梁单元上。

1.4 数值方法验证

利用Mehta等研究中的算例验证子导线电磁力计算程序的正确性,双分裂导线档距为304.8 m,弧垂为12.192 m,分裂间距为0.457 m,电流大小为10 kA,θ为每根子导线受电磁力吸引后与垂直方向的角度。电磁力作用下双分裂导线状态如图3所示。引入参数

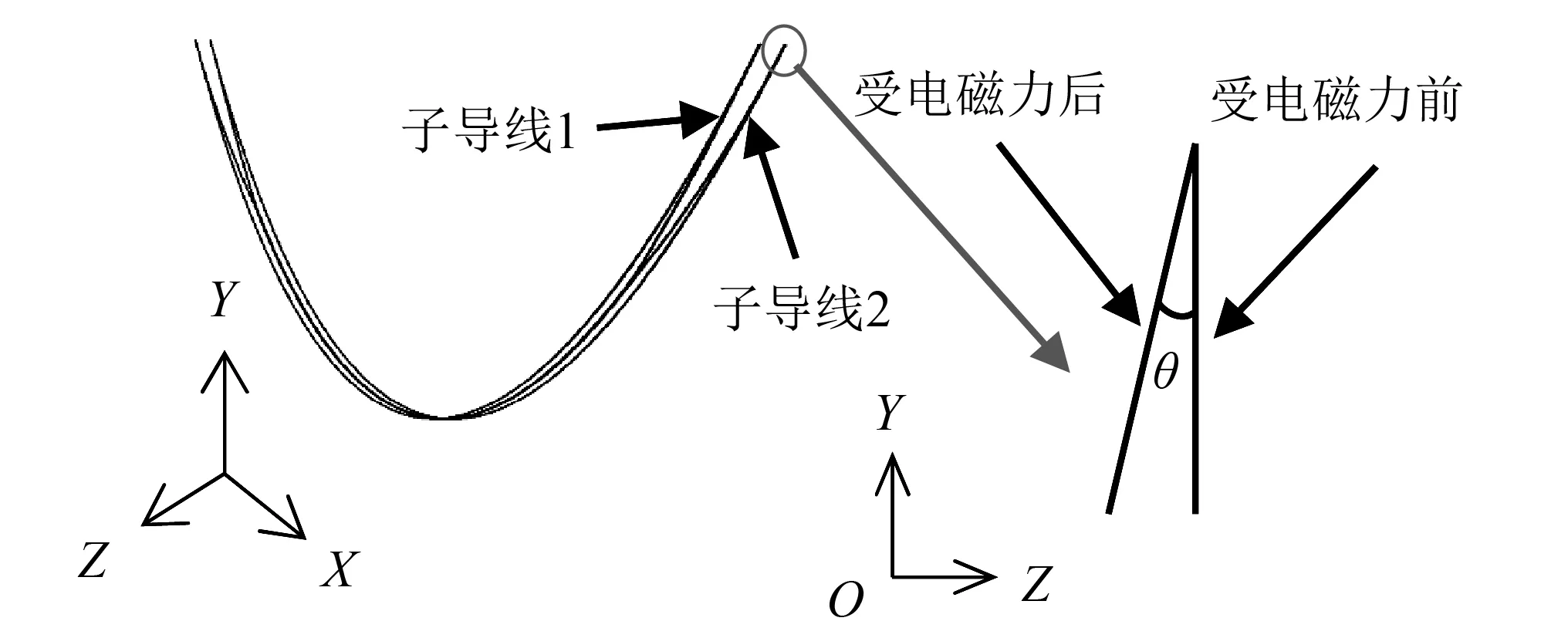
图3 电磁力作用前后双分裂导线状态Fig.3 States of twin bundle conductor before and after action of electromagnetic force

(12)

计算不同角度下导线所受电磁力。其中,θmax为两根子导线在档距中点处接触时的最大角度。

利用用户自定义程序UEL计算在不同参数λ下每根子导线沿线分布的电磁力,结果如图4所示。所得计算结果与Mehta等研究的结果完全一致,验证了用户自定义程序计算子导线电磁力的正确性。

图4 不同参数λ下双分裂导线电磁力分布Fig.4 Electromagnetic force distribution of twin bundle conductor under different parameters λ

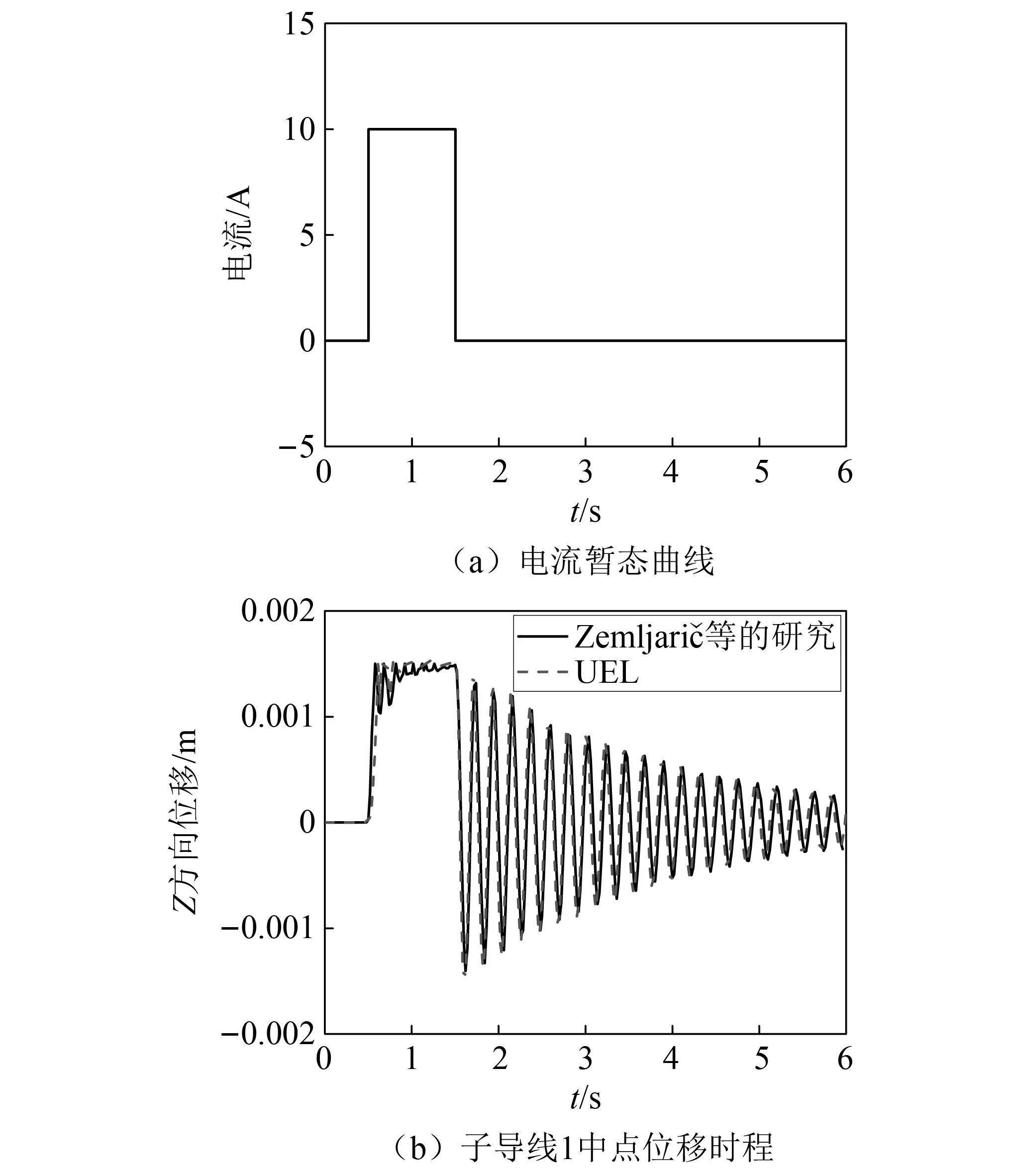
图5 暂态电流作用下双分裂导线位移响应Fig.5 Displacement responses of twin bundle conductor under transient current

2 短路电流下分裂导线运动及间隔棒载荷

2.1 220 kV双回交流输电系统短路电流仿真

为计算发生短路故障时分裂子导线所受的电磁力,需得到短路时流经导线的电流暂态曲线。故利用MATLAB/SIMULINK软件建立220 kV双回交流输电系统的仿真模型,如图6所示。

图6 220 kV双回交流输电系统仿真模型Fig.6 Simulation model for 220 kV double-circuit AC transmission system

仿真模型的参数设置如下[20]:输电线长度共200 km。两侧理想三相电压源电压为220 kV,电源内阻为0.892 9 Ω,电源电感为16.58 mH,相位分别为0°和20°。输电线正序和零序阻抗分别为0.012 73 Ω/km和0.386 4 Ω/km,正序和零序感抗分别为0.933 7 mH/km和4.126 4 mH/km,正序和零序容抗分别为0.012 74 μF/km和0.007 751 μF/km。三相短路故障发生器的故障点电阻及接地电阻均为0.001 Ω,缓冲电阻为1×10-6Ω,缓冲电容为inf。求解器选择ode45算法,短路故障发生时间为0.2 s,仿真时间共1.0 s。

通过改变电力系统仿真模型中分布参数线路1和分布参数线路2的长度以及三相短路故障发生器设置,可以实现输电线路不同位置不同短路形式的短路故障仿真。将短路后故障位置的电流暂态曲线的峰值取为短路电流,如表1所示。如图7所示为典型短路时电流暂态曲线,将其用于数值模拟分裂导线动力响应中子导线电磁力的计算。

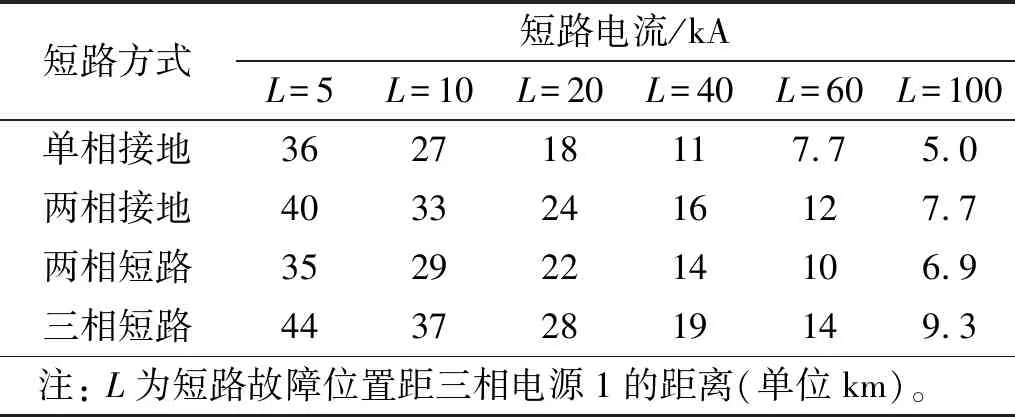
表1 不同短路故障形式下各位置短路电流

图7 典型双分裂线路短路故障电流暂态曲线Fig.7 Typical transient curves of short-circuit fault currents on twin bundle line

2.2 双分裂导线有限元模型

利用ABAQUS/CAE建立电磁力作用下双分裂导线有限元模型,如图8所示。子导线采用空间圆截面梁单元模拟,材料参数由导线型号确定。经过单元收敛性检查,模拟导线的单元长度设置为0.2 m可以满足收敛。二分裂间隔棒简化为直杆,计算其等效密度使其质量与实际间隔棒相同,杨氏模量为72 GPa,泊松比为0.27,并采用空间梁单元离散。间隔棒数量及布置位置按照实际线路档距及布置方案确定。子导线与间隔棒的连接方式采用beam连接单元模拟。边界条件为导线两端完全固定,子导线间设置接触,接触属性为硬接触。

图8 双分裂导线受电磁力作用有限元模型Fig.8 Finite element model of twin bundle conductor under electromagnetic force

模拟中子导线施加初始张力、重力和电磁力,间隔棒施加重力荷载。当考虑风载荷作用时,根据DL/T 5551—2018《架空输电线路荷载规范》[21],作用于导线上单位长度上的风载荷按式(13)计算

(13)

式中:βC为导线阵风系数;αL为档距折减系数;μZ为风压高度变化系数;μSC为导线体型系数;d为导线外径;B1为导线覆冰风载荷增大系数;V0为基本风速;θ为风向与导线或地线方向之间的夹角。这些系数的计算和取值详见DL/T 5551—2018《架空输电线路荷载规范》。所有子导线均施加风压载荷,并忽略迎风侧子导线尾流对背风侧子导线的影响。假设风沿水平方向垂直作用于线路,由于间隔棒受风面积较小,忽略间隔棒所受风压作用。导线阻尼采用瑞利阻尼,阻尼比取2%[22]。

2.3 分裂导线动力响应及间隔棒载荷特性

首先分析一档距100 m无高差孤立档双分裂线路。导线型号LGJ-300/40,分裂间距为0.4 m,子导线初始张力23 090 N。沿档等间距安装两个间隔棒。取2.1节中L=40 km时单相接地短路下的电流暂态曲线,数值模拟在短路电流为11 kA时的子导线和间隔棒的动力响应。

如图9所示为该线路导线初始平衡、短路后0.34 s和0.71 s时的状态。可见,在短路后0.34 s时,次档距Ⅱ中两子导线在电磁力作用下发生了明显的吸引,在0.71 s时电磁力减小,两子导线呈张开状态。图10所示为短路电流作用下该导线和间隔棒的动力响应。从图10(a)可见,子导线在电磁力作用下相互吸引,间距变小,且次档距II中点处子导线位移最大,间距最小。此外,由于短路电流较小,两子导线没有发生接触碰撞,做呼吸运动。从图10(b)可见,导线的呼吸运动对间隔棒产生轴向的交变冲击作用,且间隔棒主要受压。

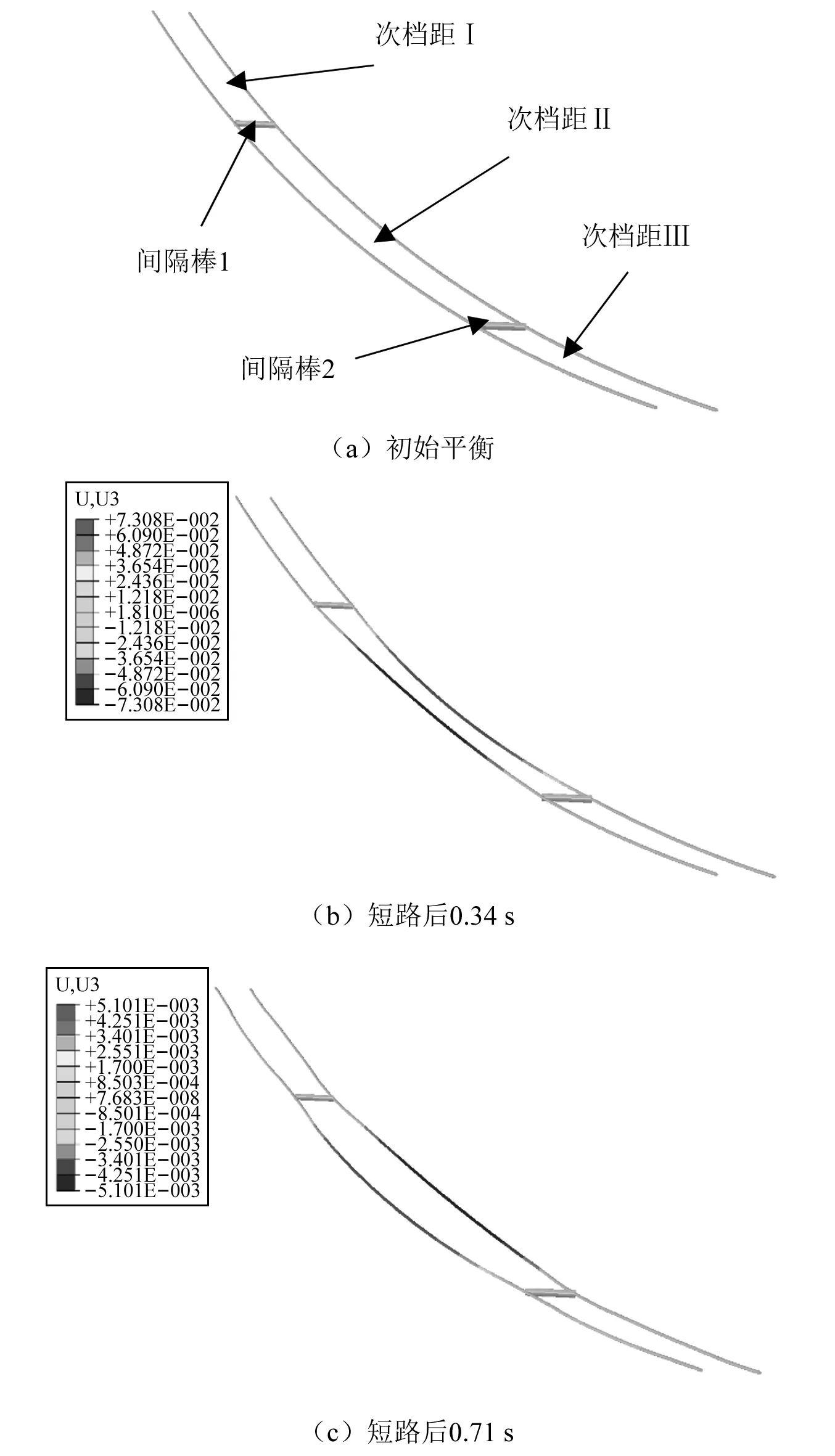
图9 短路电流作用下档距100 m线路不同时刻状态Fig.9 States of 100 m-span line at different times under short-circuit currents

图10 短路电流作用下档距100 m线路导线和间隔棒动力响应Fig.10 Dynamic responses of conductor and spacer in 100 m-span line under short-circuit current

分析档距300 m无高差孤立档双分裂线路。导线型号及其他参数与前者相同。沿档等间距安装6个间隔棒。取2.1节中L=5 km时单相接地短路下的电流暂态曲线,数值模拟在短路电流为36 kA时的子导线和间隔棒的动力响应。

如图11所示为该线路初始平衡、短路后0.08 s和0.4 s时的状态。图12所示为短路电流作用下该导线和间隔棒的动力响应。从图12(a)可见,由于短路电流大,产生的电磁力使两子导线之间的距离逐渐减小为零,发生接触碰撞,之后发生反弹,最后保持吸附状态。从图12(b)可见,间隔棒向心力在子导线接触后迅速增大并伴有高频响应,随着时间的增加,间隔棒向心力的变化趋于稳定。

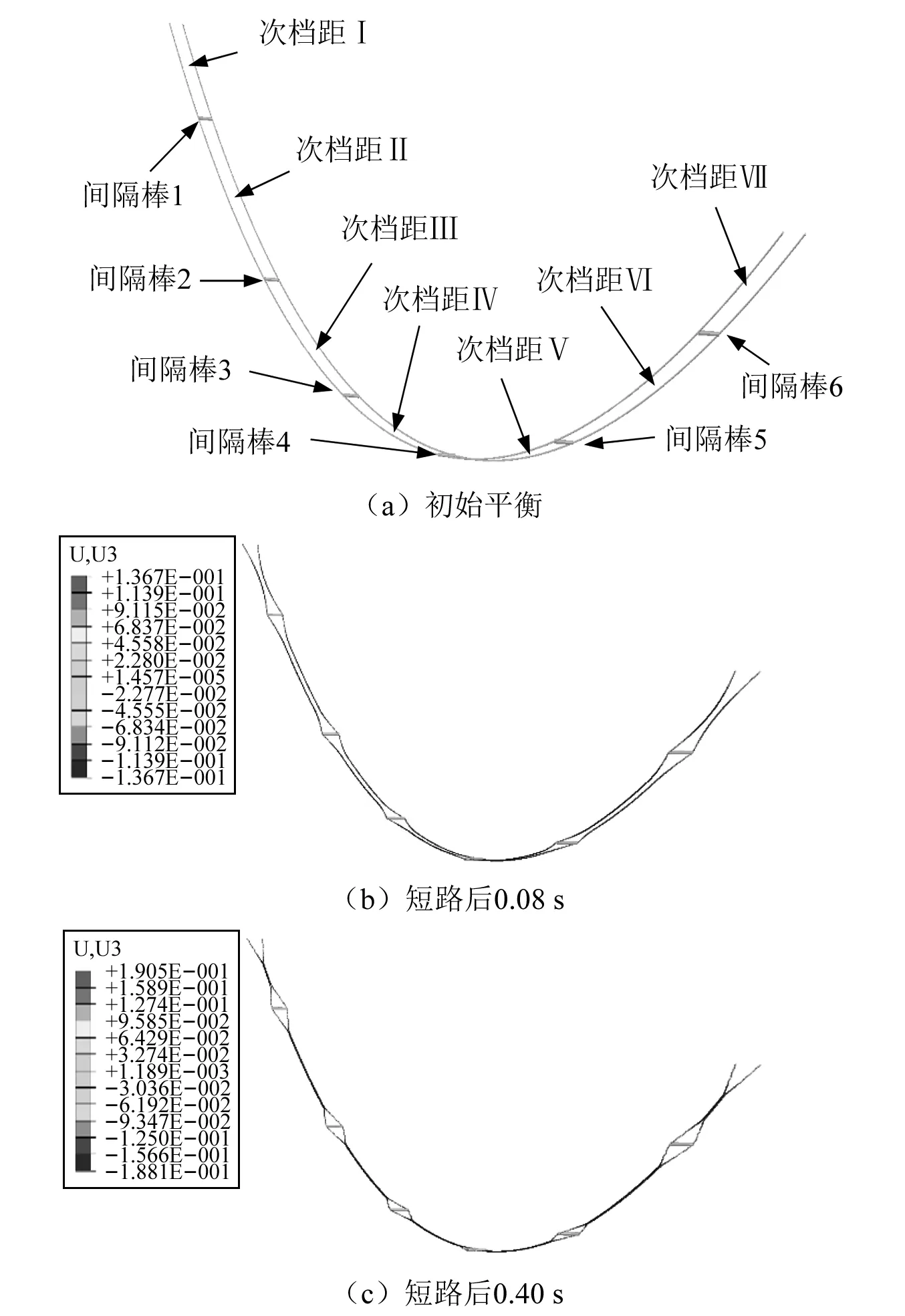
图11 短路电流作用下档距300 m线路不同时刻状态Fig.11 States of 300 m-span line at different times under short-circuit currents

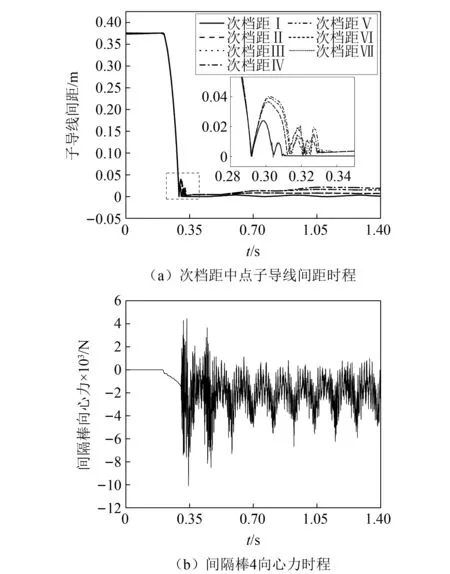
图12 档距300 m线路短路电流作用下导线和间隔棒动力响应Fig.12 Dynamic response of conductor and spacer 4 in 300 m-span line under short-circuit currents

由以上分析结果可见,短路电流作用下分裂导线动力响应可能出现两种情况:小短路电流时导线做呼吸运动,大短路电流时子导线会发生接触碰撞,两种情况下间隔棒的载荷特性不同。

2.4 间隔棒载荷规程计算方法

我国间隔棒设计规程中间隔棒向心力采用式(14)计算

(14)

式中:P为短路电流向心力,N;ICC为短路电流,kA;n为子导线根数;H为子导线张力,N,通常为25%导线拉断力;S为子导线分裂圆直径,mm;D为子导线直径,mm。该公式没有考虑档距和间隔棒安装个数和位置的影响。

利用式(14)计算2.3节中两个算例中间隔棒向心力,当短路电流为11 kA时间隔棒向心力规程计算值为2 876 N,数值模拟最大值为197 N,规程计算值远大于数值模拟结果。短路电流为36 kA时规程计算值为9 413 N,数值模拟最大值为10 383 N,规程计算值小于数值模拟结果。

3 间隔棒载荷特性参数分析

短路故障时间隔棒所受载荷受输电线路结构、短路电流和风速的影响,这些参数包括导线型号、档距、高差、间隔棒个数和排布方式、子导线分裂间距、初始张力、短路电流和风速等。利用2.2节有限元建模方法模拟分析这些参数对间隔棒向心力最大值的影响规律,并与规程计算方法进行比较。

3.1 短路电流的影响

为研究短路电流对间隔棒向心力最大值的影响,建立档距为100 m,分裂间距为0.4 m,等间距排布两个间隔棒的孤立档输电线路。选用的导线型号及其物理参数如表2所示,子导线初始张力均为23 090 N。数值模拟在短路电流分别为5 kA,8 kA,11 kA,18 kA,27 kA,33 kA,37 kA,40 kA和44 kA时的间隔棒向心力最大值,并且将数值模拟结果与规程中间隔棒向心力计算方法进行对比。

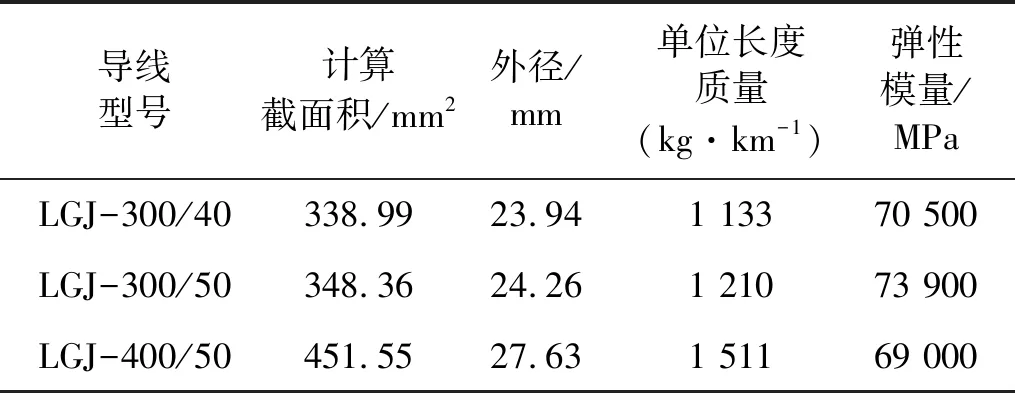
表2 导线物理参数

图13为数值模拟与规程公式计算得到的不同型号导线在不同短路电流下的间隔棒向心力。从图13可以看出,不同型号导线在相同短路电流下计算得到的间隔棒向心力相差很小。由表2和式(14)可知,3种型号的导线外径相差较小,规程公式计算得到的间隔棒向心力差距较小。数值模拟结果也反映出导线型号对间隔棒向心力影响不明显。此外,两种方法计算得到的间隔棒向心力均随短路电流的增加而增加,但规程公式计算值与短路电流呈线性关系,而数值模拟结果呈非线性关系,这是因为导线电磁力与电流大小的平方成正比。值得注意的是,在短路电流较小时,规程公式计算的间隔棒向心力大于数值模拟结果,在短路电流较大时,规程公式计算值小于数值模拟值。

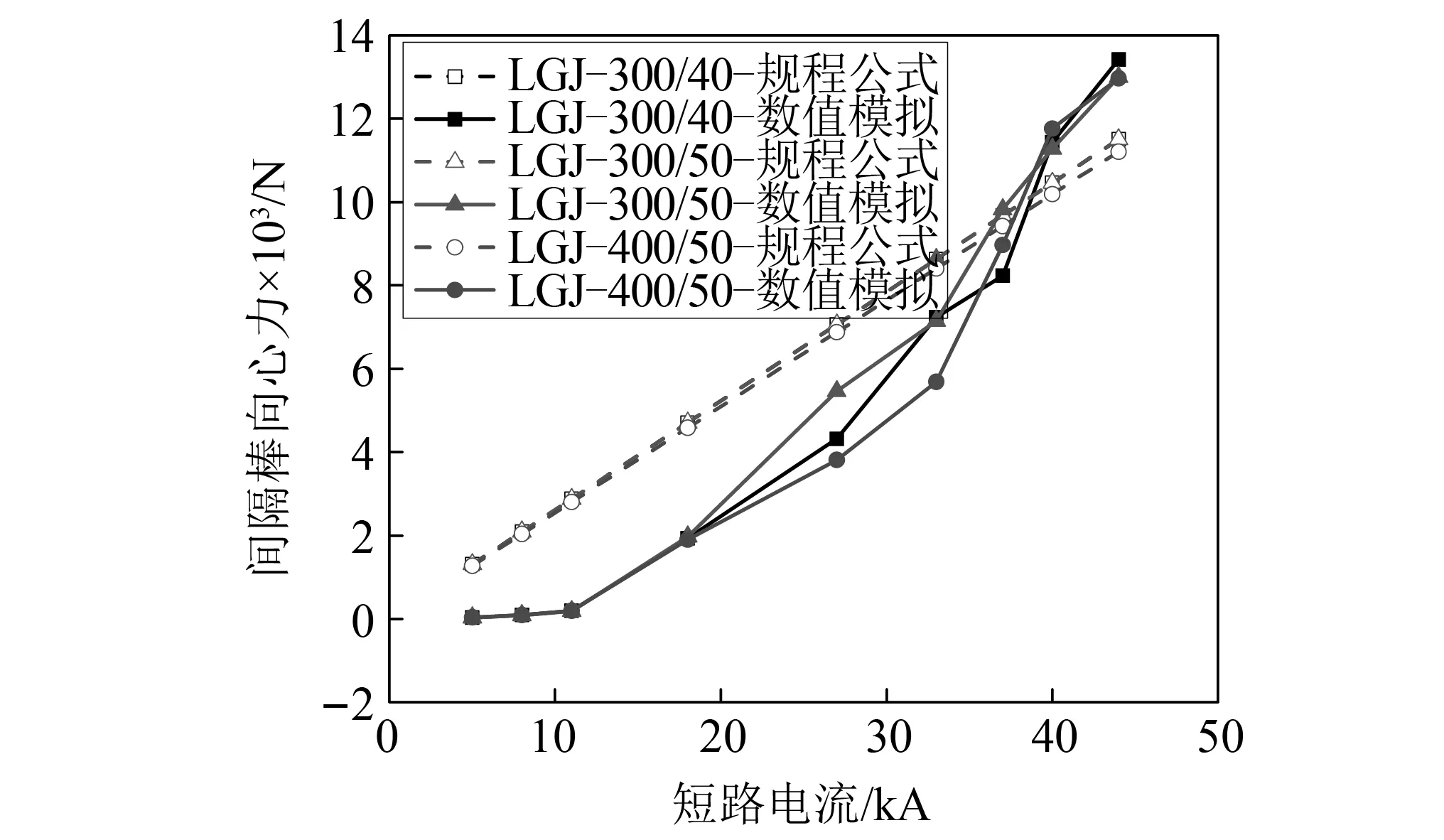
图13 间隔棒向心力随短路电流的变化Fig.13 Variation of centripetal force of spacer with short-circuit current

3.2 档距和间隔棒排布方式的影响

输电线路的档距与间隔棒排布方式不同会影响输电线路的次档距大小及分布,从而影响间隔棒向心力大小,但是规程公式中没考虑该影响。为研究这种影响,建立不同档距的孤立档输电线路,分裂间距为0.4 m,导线型号为LGJ-300/40,初始张力为23 090 N。间隔棒个数和布置方式如表3中所列。数值模拟各种参数条件下短路电流为36 kA时间隔棒向心力最大值。

表3 不同档距线路间隔棒布置方案

图14所示数值模拟得到的不同档距线路在短路电流作用下各间隔棒最大向心力。可见,等间距排布方式下,间隔棒个数越少,间隔棒向心力越小。在相同间隔棒个数下,非等间距排布方式下间隔棒向心力小于等间距排布方式。同档线路中各间隔棒的受力大小均不同。这是由于间隔棒所受向心力受其两侧次档距长度影响。等间距排布方式下,次档距越长,间隔棒两侧导线张力沿间隔棒方向的合力越小,从而使间隔棒向心力减小。非等间距排布方式下,间隔棒两侧次档距不同,从而使两侧导线张力的合力不再沿间隔棒轴向,从而使间隔棒向心力减小。

3.3 子导线分裂间距和初始张力的影响

为研究子导线分裂间距对间隔棒向心力最大值的影响,建立档距为100 m,分裂间距分别为0.4 m,0.45 m和0.5 m,等间距排布两个间隔棒的孤立档线路。导线型号为LGJ-300/40,初始张力为23 090 N。数值模拟在短路电流为36 kA和44 kA时的间隔棒向心力最大值。

模拟得到的不同子导线间距下的间隔棒向心力如图15所示。从图5可见,数值模拟结果和规程公式计算得到的向心力均随着子导线分裂间距增加而增加,这是因为较大的分裂间距使子导线在吸附时具有较大的导线张力,从而使间隔棒所受载荷变大。

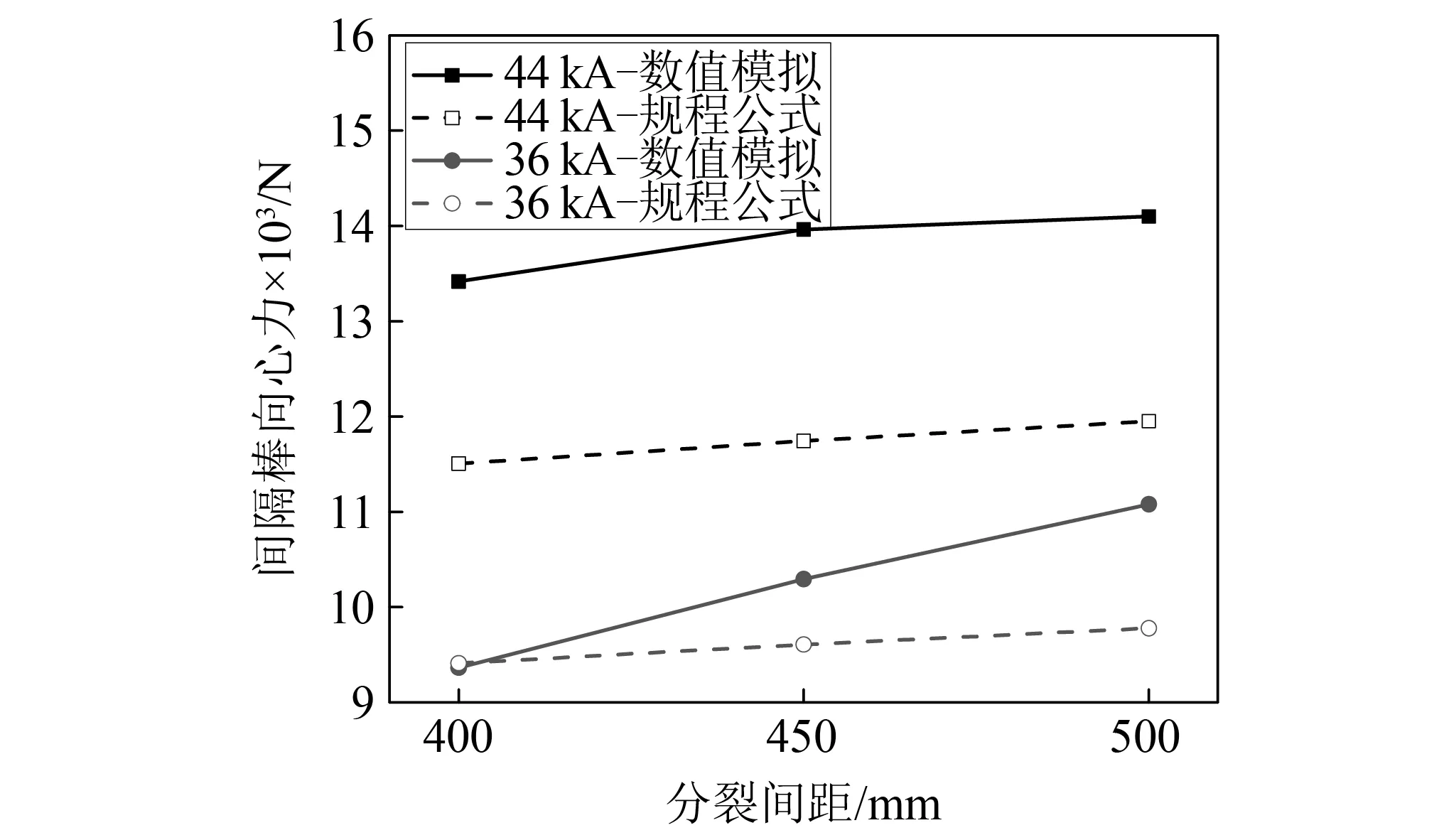
图15 间隔棒向心力随分裂间距的变化Fig.15 Variation of centripetal force of spacer with bundle spacing

为研究子导线初始张力对间隔棒向心力最大值的影响,建立了档距为400 m,分裂间距为0.4 m,等间距排布7个间隔棒的孤立档输电线路,导线型号为LGJ-300/40,子导线初始张力分别为13 854 N,18 472 N,23 090 N,27 708 N和32 326 N。当数值模拟短路电流为36 kA和44 kA时的间隔棒向心力最大值。

模拟得到的不同导线初始张力情况下间隔棒向心力如图16所示。从图16可见,数值模拟结果和规程公式均说明间隔棒向心力随着导线初始张力的增大而增大且几乎呈线性变化。这是因为较大的导线初始张力会增大导线的几何刚度,使得间隔棒在导线吸附过程中所受载荷增加。

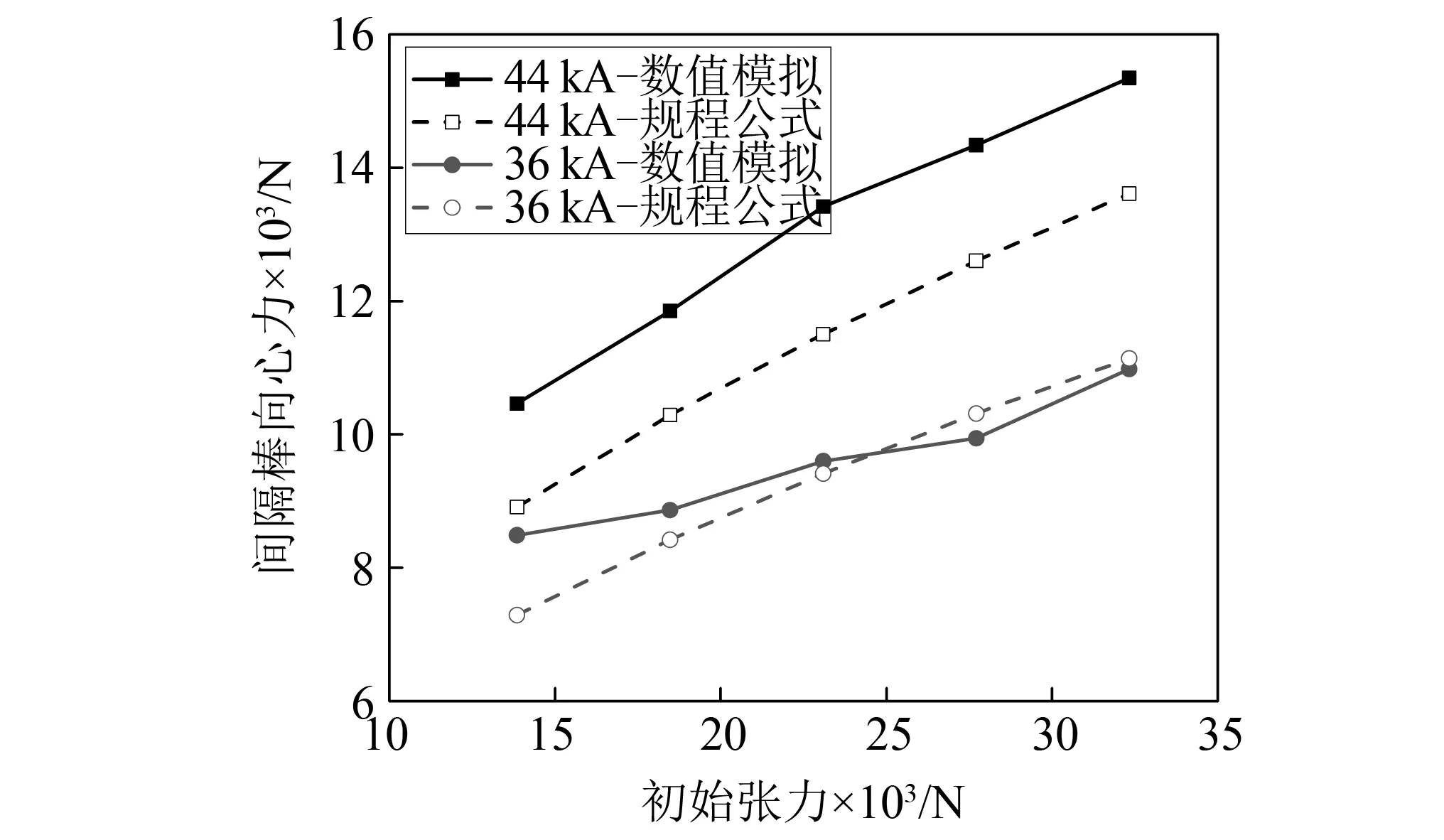
图16 间隔棒向心力随初始张力的变化Fig.16 Variation of centripetal force of spacer with initial tension

3.4 高差的影响

为研究高差对间隔棒向心力最大值的影响,建立了档距400 m,高差分别为0,40 m,80 m和120 m,分裂间距为0.4 m,等间距排布7个间隔棒的孤立档线路。导线型号为LGJ-300/40,初始张力为23090 N。数值模拟在短路电流为36 kA和44 kA时的间隔棒向心力最大值,得到的结果如图17所示。从图17可见,高差对间隔棒向心力影响较小,这是由于高差对导线吸附时所受电磁力和张力的影响不大所致。

图17 间隔棒向心力随高差的变化Fig.17 Variation of centripetal force of spacer with elevation difference

3.5 风速的影响

为研究风速对间隔棒向心力最大值的影响,建立了档距为400 m,分裂间距为0.4 m,非等间距排布7个间隔棒的孤立档输电线路,导线型号为LGJ-300/40,风速分别为0,5 m/s,10 m/s,15 m/s,20 m/s,25 m/s和30 m/s。数值模拟短路电流为36 kA和44 kA时稳定风作用下间隔棒向心力最大值。模拟中忽略了迎风侧子导线对背风侧子导线气动力的影响。

模拟得到的短路故障时不同风速下间隔棒向心力如图18所示。从图18可见:当风速较低时对间隔棒向心力影响较小;当风速较大时,随风速的增大而增大。这是因为风速较大时导线的张力也较大,从而使间隔棒所受载荷增加。

图18 间隔棒向心力随风速的变化Fig.18 Variation of centripetal force of spacer with wind speed

4 结 论

本文提出了模拟发生短路故障时分裂导线和间隔棒动力响应的数值方法,针对典型双分裂线路,利用该方法对不同短路电流、线路结构参数和风速下间隔棒载荷特性进行了模拟分析,得到以下结论:

(1)利用提出的模拟分裂导线在短路电流作用下动力响应的数值方法,模拟了文献中给出的双分裂导线短路模型试验,验证了本文方法的正确性和可行性。

(2)对双分裂导线短路电流作用下动力响应的数值模拟结果表明:当短路电流较小时,规程公式计算得到的间隔棒向心力大于数值模拟值;当短路电流较大时,规程计算值小于数值模拟值,因此在大短路电流情况下按现有规程设计间隔棒偏于危险。

(3)参数分析结果表明——线路的档距、间隔棒数量及位置会影响短路故障发生时间隔棒的载荷大小,而现有规程没有考虑这些影响;较少的间隔棒数量和非等间距排布方式会降低短路故障时间隔棒所受最大载荷;间隔棒向心力随子导线分裂间距和初始张力增加而增大,实际工程中采用较小的分裂间距和导线初始张力有利于降低间隔棒在短路故障时所受的载荷;间隔棒向心力随着风速的增加而增大,在设计中考虑风速影响时,应适当提高间隔棒的强度。