高温超导磁悬浮列车振动特性分析及其参数可行域研究

张明亮, 杨新梦, 刘丽茹, 李明远

(1. 石家庄铁道大学 机械工程学院,石家庄 050043;2. 兰州交通大学 光电技术与智能控制教育部重点实验室,兰州 730070)

磁悬浮列车按工作原理主要分为3种:常导电磁悬浮列车(electric magnetic suspension magnetic levitation,EMS Maglev)[1],低温超导电动磁悬浮列车(electro dynamic suspension magnetic levitation,EDS Maglev)[2-3],高温超导磁悬浮列车(high temperature superconducting magnetic levitation,HTS Maglev)[4-7],不同类型磁悬浮列车的建模及研究方法也各不相同[8]。EMS Maglev以德国为代表,EDS Maglev以日本为代表,而HTS Maglev则以中国为代表,且该类磁悬浮制式我国具有自主知识产权,故本文以高温超导磁悬浮列车为研究对象。高温超导磁悬浮列车利用高温超导体的磁通钉扎效应,与永磁轨道产生宏观的悬浮力使两者保持稳定悬浮状态。西南交通大学建立了试验样车,可以测得高温超导磁悬浮列车运行时超导体与永磁体之间的悬浮间隙和对应的悬浮力。2015年,王家素等[9]综述了高温超导磁悬浮列车的研究现状和探讨该类磁悬浮列车实现高速的可能性。2019年,马光同等[10]系统阐释了超导磁浮交通的研究进展,并指出了高温超导磁悬浮的优点和缺点。2020年,陈楠等[11]以实现大载重为目标,提出了一种高温超导-永磁混合悬浮车系统概念及理论设计方法。同年,李家志等[12-13]论述了二代高温超导线(带)材、高温超导块材在超导磁悬浮列车上的应用形式和特点。上述研究表明了高温超导磁悬浮列车的可行性及其可扩展性,并且论证了高温超导磁悬浮列车是未来轨道交通的发展重点之一。

除了在轨道交通的应用,李杨等[14]提出高温超导体用于电磁推进的设想。高策等[15]研究了高温超导体用于在轨重构的磁通钉扎接口。Zhang等[16-17]提出了高温超导体用于电磁对接机构,并研究了其控制性能和力学特性。韩乐等[18]以高温超导块材在同步直线电机应用为目标,试验研究了所受电磁力和俘获磁通随充磁电流、电机初级三相交流电幅值与频率等参数的变化规律。余志强等[19-20]研究了高温超导轴承和飞轮储能系统样机的性能。

在高温超导试验仿真方面,蒋冬辉[21]建立了三维电-磁-热多物理场耦合的高温超导磁悬浮振动模型,研究了自由悬浮状态下和运行状态下高温超导体的振动响应特性。武倩倩等[22]搭建了高温超导磁悬浮列车的隔振系统,研究了系统在不同激励扰动下的动力学响应。江东等[23]利用磁悬浮振动测试系统的仿真模型,研究了该系统产生混沌的边界条件,并通过参数优化使系统重新回到稳定状态。Che等[24]通过试验研究,得到了场冷条件下高温超导磁悬浮列车在曲线行驶时具有更加稳定的结论。2022年,Zhang等[25]利用动力学软件仿真分析了高温超导磁悬浮列车在直线运行的性能,同年,该团队又提出了一种等效处理高温超导块组合的方法,简化了计算过程[26]。

除此之外,李晓龙等[27]研究分析PEMS(permanent and electrical magnetic suspension)型低速磁悬浮单点模型时,发现可以通过设置非线性饱和环节和动态调整饱和阈值,从而抑制车轨耦合振动来使系统达到稳定的现象。张兴义等[28]研究了零场冷和场冷条件下高温超导块悬浮力的时间弛豫特性,结果表明弛豫特性与超导体内部复杂的微观结构有关。尽管上述研究取得了较为丰富的成果,但是目前对于高温超导磁悬浮列车的垂向自由振动特性研究少有报道,本文根据悬浮力试验数据构造悬浮力数学模型,建立垂向振动的动力学模型,研究其自由振动响应,根据磁悬浮标准分析参数的可行域,其研究规律对高温超导磁悬浮列车的磁轨关系参数设计具有指导意义。

1 高温超导磁悬浮列车的工作原理

高温超导磁悬浮列车的工作原理依靠的是高温超导体的磁通钉扎效应,如图1所示。其操作步骤为:将高温超导体与永磁体保持适当距离(一般以mm为单位),这时对应的距离为场冷高度。而后添加液氮使高温超导体冷却,待其温度降低冷却后,高温超导体内部的钉扎点可以捕获永磁体的部分磁场,这时高温超导体与永磁体之间产生宏观的磁力,该力为高温超导磁悬浮列车需要的悬浮力,悬浮力使两者呈现出一种非接触的连接状态,从而保证高温超导体稳定悬浮在永磁体之上。

图1 高温超导体磁通钉扎特性原理示意图Fig.1 Schematic diagram of magnetic flux pinning effect of high temperature superconductors

2 悬浮力测量试验

2.1 试验装置

高温超导体和永磁轨道之间的悬浮力的大小、变化趋势直接影响着列车的稳定性,本文利用试验装置测试得到不同悬浮间隙下的悬浮力,其悬浮力试验装置如图2所示,试验装置的测试原理如图3所示。将高温超导体固定在液氮低温容器中,并固定在移动架上。位移传感器位于高温超导体移动架和基座之间,压力传感器位于永磁轨道和基座之间。高温超导体在电机带动下可做上下的往复移动,用位移传感器测量高温超导体和永磁轨道间的距离,用压力传感器采集悬浮力数据,由测试系统对试验数据进行处理,最后将悬浮力数据导出。

图2 悬浮力试验装置Fig.2 Testing device of suspension force

图3 悬浮力试验装置测试原理示意图Fig.3 Schematic diagram of suspension force test system

本次试验采用的是双峰永磁轨道,其材料为钕铁硼,轨道长度为800 mm,实物如图4所示,具体尺寸参数和磁化方向如图5所示,其中充磁方向为箭头方向,黑色两边采用纯铁,起着聚磁作用。为了形成较大的超导平面,高温超导体利用多个高温超导块组合起来,简称高温超导块组合,具体采用10块YBCO高温超导块,单块尺寸为Φ30 mm×14 mm,按5×2的方式排列。

图4 永磁轨道实物Fig.4 The diagram of permanent magnet track

图5 永磁轨道横截面图(mm)Fig.5 Cross section diagram of permanent magnet track (mm)

2.2 试验结果

本次试验设置的场冷高度为22 mm,以悬浮间隙(z)为横坐标,悬浮力(Fz)为纵坐标,得到不同悬浮间隙下的悬浮力,如图6所示。

图6 悬浮力和悬浮间隙的关系Fig.6 Relationship between levitation force and levitation gap

由图6可知:在场冷高度处(22 mm)悬浮力为0,不受力,即这个位置为不受重力影响下的平衡点;在悬浮间隙大于场冷高度情况下,作用力小于0,表明作用力的方向与悬浮间隙方向z相反,该力使高温超导块组合和永磁轨道之间处于相互吸引的状态,防止两者离开平衡位置和一旦离开平衡位置后具有恢复到平衡位置的能力。同时可观察到悬浮力大小随悬浮间隙的增大先增大后减小,悬浮力与悬浮间隙呈明显的非线性关系。

3 高温超导磁悬浮列车垂向动力学模型的建立

为了研究磁悬浮列车的振动特性,本文利用高温超导块组合和永磁轨道的磁轨关系(悬浮力),构造两者的悬浮振动系统(简称为超导振子)。以重力的方向为负方向,平衡位置处为原点建立坐标系,其振子的模型如图7所示。

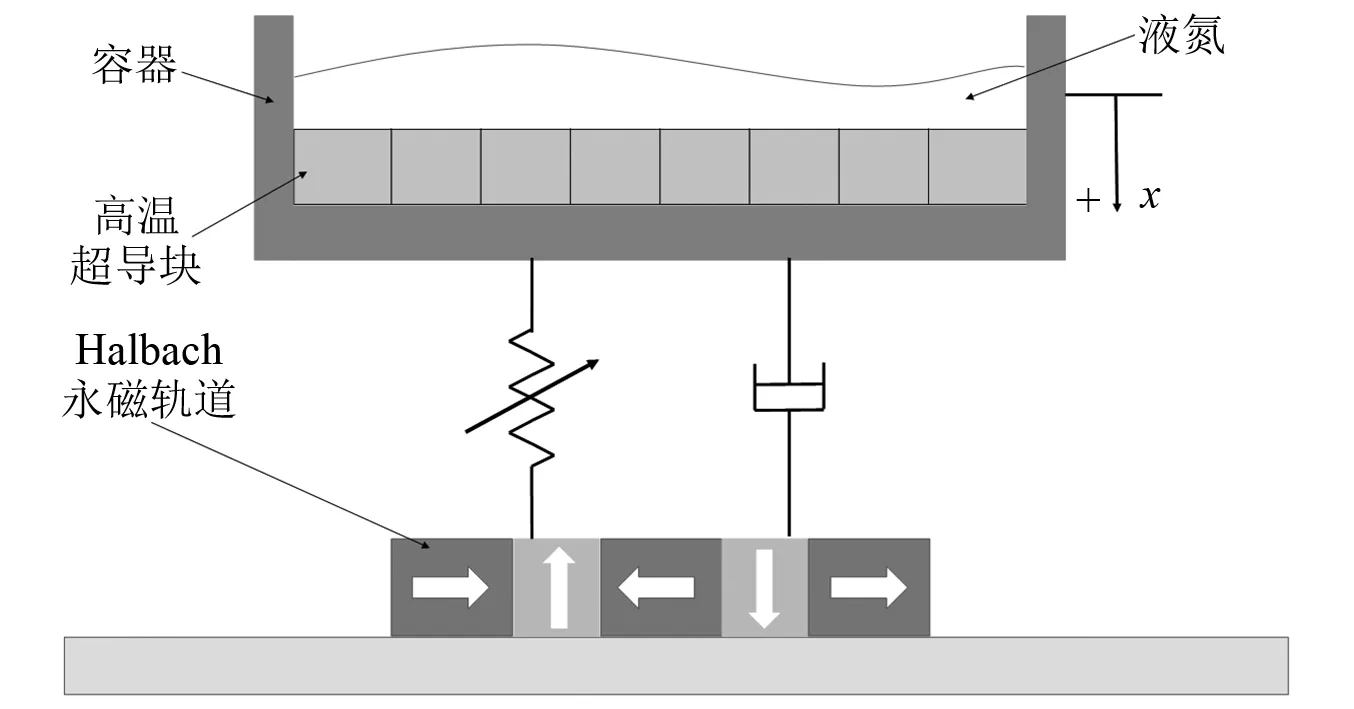
图7 高温超导磁悬浮列车的超导振子模型Fig.7 Vibrator model of HTS Maglev

为了解析建模,需将测得的悬浮力与悬浮间隙之间的试验数据进行拟合建立经验公式,本文采用的表达形式如下

Fz=k3zz3+k1zz+k0z

(1)

式中:z为高温超导块组合和永磁轨道之间的垂向间隙,mm;k3z为三次方的系数,N/m3;k1z为一次方的系数,N/m;k0z为常数项。

式(1)的平衡点为场冷高度位置,由于振子同时还受到重力的作用,故振子所受合力为

Fs=-mg+k3zz3+k1zz+k0z

(2)

式中,m为振子的质量,kg。

由式(2)可以观察到振子的质量(包括净重和载重)仅影响悬浮位置(平衡点),但不影响合力的线性和非线性刚度系数。考虑到式(2)的平衡点不是0点(坐标原点),为研究方便,需根据坐标平移原理将非0平衡点移动到0点,假定其平衡点为zs,将垂向间隙z减去zs得到悬浮间隙u,u的表达式为

u=z-zs

(3)

将式(3)代入式(2),整理得到平衡点附近的合力与悬浮间隙的关系

-Fs=k1u+k3u3

(4)

式中:k1为线性刚度,N/m,由拟合结果得出;k3为非线性刚度,N/m3,由拟合结果得出。

根据式(4),可得平衡点附近合力与悬浮间隙的拟合关系和试验数据对比结果,如图8所示。

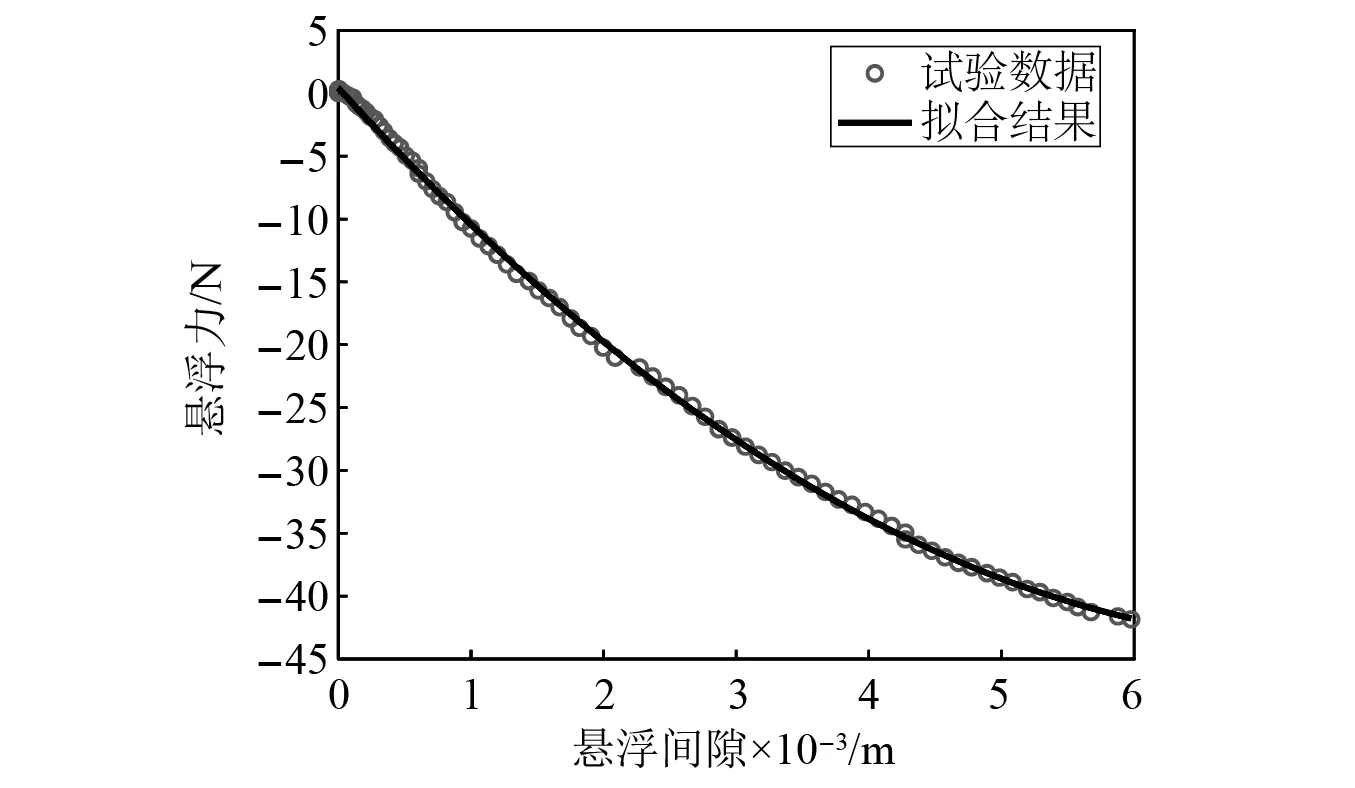
图8 坐标平移后试验数据及其拟合曲线Fig.8 Test data and fitting curve after coordinate translation

根据牛顿第二定律,建立超导振子的运动微分方程

(5)

由式(3)可得到

(6)

将式(4)和式(6)代入式(5),可得

(7)

式中,c为线性阻尼系数,Ns/m。

超导振子的动力学模型包含线性阻尼力、线性弹簧力和三次方的非线性弹簧力,等效成Duffing振子,其一次近似求解可采用非线性动力学理论的多尺度法进行推导[29]。

4 超导振子模型的一次近似解

由于式(7)一般为强非线性系统,为了能够利用经典的多尺度法求解其近似解析解,需对式(7)的微分方程进行无量纲尺度变换[30-31],将其变成弱非线性系统。本文引入长度和时间尺度,其表达式为

(8)

式中:p为长度尺度;q为时间尺度。

由式(8)可得

(9)

将式(9)代入式(7),对其进行整理可得

(10)

根据多尺度法求解的要求,非线性项和阻尼项必须是小量,需要对其进行约束变形,其表达式为

(11)

将式(11)代入式(10)可得到

(12)

(13)

根据多尺度法,式(12)的解的一般表达式为

(14)

将式(13)与式(14)代入式(12),对比ε同次幂系数得到线性偏微分方程如下

(15)

(16)

根据线性方程求解理论,易得式(15)的解为

(17)

式中:cc为前部分的共轭部分,将式(17)代入(16),为消除永年项,需满足以下的关系

(18)

式中,B(T1)为A(T1)的共轭函数。

根据多尺度法,可将A(T1)表达为

(19)

联立式(18)和式(19),分离实部与虚部,整理得到

(20)

对式(20)进行求解,可以得到

(21)

式中:c1为常数1;c2为常数2。

对式(21)的初始条件进行赋值,即可得到c1和c2,采用常取的初始条件(初始位移和初始速度)的取值如下

可得

根据尺度变换式(8)和坐标平移原理可得超导振子垂向自由振动情况下的一次近似解为

(22)

为验证一次近似解表达式的正确性,将式(22)进行求导得到速度表达式。将解析解(位移和速度)响应与数值解响应进行对比,对比结果如图9所示,仿真分析参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

图9 解析解与数值解对比图Fig.9 Comparison between analytical solution and numerical solution

由图9可知,超导振子的位移和速度都随着时间的增加呈现震荡衰减的趋势,并且解析解在位移和速度两个方面与数值解吻合较好,从而证明解析解的正确性。因此可利用解析解表达式研究面向高温超导磁悬浮列车的超导振子垂向振动的动态特性。

5 超导振子的响应特性和参数可行域分析

5.1 安全性指标

在振动过程中,假定高温超导体初始时刻振动达到允许最大安全振幅(距离平衡点zs的最大距离)为zstr,该值由磁悬浮标准决定,且令zstr>0。可得

|z0(0)-zs|=zstr

将上述代入式(22)整理得到

(23)

将式(23)代入式(22)整理可得

(24)

后续研究均在式(24)的约束前提下进行,即在满足初始时刻处在允许最大安全振幅的要求下进行系统参数的影响和可行域研究。

5.2 舒适性指标

为了使列车乘客乘坐感受更舒适,需要对最大加速度进行约束。将式(24)进行两次求导并整理,得到振子模型的加速度表达式

(25)

其中

将式(25)的上限设定为最大加速度amax,可得

(26)

为了研究方便,将单位质量的阻尼定义为比阻尼αcm,单位质量的刚度定义为比刚度αk1m,可得

(27)

将式(27)代入式(24),可得

(28)

利用式(28)可研究在满足安全性指标的前提下系统参数比阻尼和比刚度对最大加速度的影响,为了定量分析其影响规律,将式(28)对比阻尼和比刚度求偏导,得到其偏导数关系。根据舒适性要求设定列车允许的最大加速度为amax,str(大于0),根据式(28)得到在舒适性的要求下系统参数需满足的条件如下

f(αcm,αk1m)=amax-amax,str≤0

(29)

利用式(29)可探寻系统参数的可行区域。

5.3 分析与讨论

由式(28)和偏导数关系可知最大加速度受比阻尼和比刚度的综合影响,表现非线性规律。为了研究其变化规律,给定一定范围,对其进行可视化分析。根据磁悬浮安全标准,可得允许最大安全振幅设置为zstr=5 mm,根据多尺度法常取数值a0=1,μ=1,由式(28)可得最大加速度与系统参数的关系,如图10所示。

图10 系统参数对最大加速度的影响规律Fig.10 Effect of system parameters on maximum acceleration

由图10(a)和图10(b)可知,最大加速度随着比阻尼与比刚度的增大而增大,并且比阻尼对其影响更显著;由图10(c)可知,曲线呈向下凹的趋势,表明随着比阻尼的增大,最大加速度增加程度越来越快。由多条不同比刚度曲线分布特点知:增大比刚度会使其较为均匀地增大;由图10(d)可知,曲线呈上凸的趋势,表明随着比刚度的增大,最大加速度增加程度越来越慢。由多条不同比阻尼曲线分布特点知:随着比阻尼增大,最大加速度增大程度逐渐变快。经过上述分析,比阻尼是影响系统最大加速度的重要因素,次要因素是比刚度。为了限制最大加速度,比阻尼和比刚度应取较小值。

由式(28)可以得到最大加速度变化率与比刚度和比阻尼的关系,如图11所示。

图11 最大加速度随系统参数的变化率Fig.11 Rate of change of maximum acceleration with system parameters

由图11(a)可知,随着比阻尼增大,最大加速度的变化率为正并且逐渐增大,表明最大加速度的增速逐渐变快,且比刚度增大对最大加速度的影响逐渐减弱;由图11(b)可知,随着比刚度的增大,最大加速度的变化率为正并且逐渐降低,表明最大加速度增速逐渐变慢,且更大的比阻尼会使其变化率整体增大,即比阻尼对其变化率影响最显著,这与前面得到的比阻尼是影响最大加速度重要因素的结论相同。

由式(29)可以得到满足舒适性指标下比阻尼和比刚度应满足的条件,且两者的关系为耦合的非线性关系。根据式(29)当允许的最大加速度取2.5 m/s2经计算比阻尼超过25.7 s-1,比刚度超过500 s-2,f(αcm,αk1m)将大于0,即系统不满足舒适性要求。

为了研究其变化规律,给定一定范围,对其进行可视化分析。由式(29)可得判断函数f(αcm,αk1m)与系统参数关系,如图12所示。图12(a)中的曲面在0横截面(黑色横截面)以下对应的横纵坐标参数范围满足系统要求,图12(b)中黑色虚线是0标准线,其满足的关系式为

图12 舒适加速度范围Fig.12 Comfortable acceleration range

(30)

由图12可知,当比阻尼大于25.7 s-1或比刚度大于500 s-2时,系统一定不满足舒适性指标。需要说明的是当比阻尼小于25.7 s-1,比刚度参数不合适时,仍有可能不满足舒适性指标;同理当比刚度小于500 s-2,比阻尼参数不合适时,仍有可能不满足舒适性指标。更为重要的是系统参数的可行域呈现近似的三角形区域,系统参数要想满足舒适性指标,必须处在式(30)曲线的下方,即阴影部分。从舒适性指标的角度分析,比阻尼和比刚度宜取较小值。

6 结 论

本文将高温超导列车的悬浮力拟合成经验公式,建立了其动力学模型,采用多尺度法推导了一次近似解形式,利用近似解研究了列车自由振动的特性,确定了系统参数的可行域,主要结论如下:

(1) 通过试验装置测得不同悬浮间隙下的悬浮力,通过试验数据拟合得到磁轨关系;基于牛顿第二定律建立了高温超导磁悬浮列车的运动微分方程,利用无量纲化方法将其处理成弱非线性系统,采用多尺度法得到一次近似解析解表达式,并验证其正确性。

(2) 利用解析解表达式得到自由振动下系统的最大加速度表达式。在满足安全性指标的前提下分析了比阻尼和比刚度对最大加速度的影响,研究表明随着比阻尼和比刚度的增大,最大加速度增大,且发现比阻尼对最大加速度的影响更显著。

(3) 根据列车舒适性指标提出了一种判断系统参数可行域的解析方法,给出比阻尼大于25.7 s-1或比刚度大于500 s-2时系统一定不满足舒适性指标的结论,研究表明可行域呈现近似的三角形区域(阴影部分),且比阻尼和比刚度宜取较小值。

本文的研究揭示了高温超导磁悬浮列车自由振动的动力学行为,为该类磁悬浮列车的系统参数设计提供了理论依据。