均匀流作用下悬索桥单侧并置双主缆振动特性分析
张太科, 陈上有, 刘 高, 杨佐磊
(1. 广东省公路建设有限公司,广州 510100; 2. 广东湾区交通建设投资有限公司,广州 510100;3. 中交公路长大桥建设国家工程研究中心有限公司,北京 100088)
悬索桥是大跨度桥梁的主要桥型之一[1],早期已建成悬索桥大都采用双主缆缆索系统,只有极少数采用单侧并置双主缆的四主缆缆索系统,如美国华盛顿大桥,主跨1 067 m;另外一座是美国维拉扎诺大桥,主跨为1 298 m[2]。随着桥梁跨度的增加,通行车道的增多,采用双主缆悬索桥方案,主缆直径越来越大,主缆的制造、架设和安装将面临挑战。采用四主缆缆索系统可以大幅减小主缆直径,因此,对于超大跨桥梁,采用单侧并置双主缆的四主缆悬索桥将是一种比较好的选择。我国的燕矶长江大桥,主跨1 860 m,由于航空限高,采用了不同矢跨比的四主缆悬索桥,将成为我国首座四主缆悬索桥[3]。狮子洋大桥跨度达2 180 m,通行16车道,在初步设计阶段也提出了单侧并置双主缆的四主缆悬索桥比选方案[4]。
抗风问题是大跨度悬索桥面临的主要问题之一[5],对于单侧单主缆的双主缆悬索桥,主缆的风致振动问题主要是驰振。驰振是一种在风作用下由于结构运动产生负阻尼并导致振动发散的空气动力失稳现象。李胜利等[6-9]对大跨径悬索桥施工期暂态主缆的驰振系数及驰振临界风速进行了研究,指出在大跨径悬索桥主缆的架设过程中有发生驰振失稳的可能性,须采取控制措施。李永乐等[10]基于实桥三维驰振模型,采用时域法分析了主缆驰振性能,结果表明,主缆驰振以反对称振动为主,随着风速的增大,驰振卓越频率逐渐减小,驰振形态由高阶模态振动逐步转变为低阶模态振动,当风速较高时,驰振振幅较大,频率较单一,通常以结构竖向基阶模态为主,此时横桥向振幅较小,振动频率更低,多模态参振现象明显。
对于并置双主缆而言,迎风侧主缆对背风侧主缆存在气动干扰,即迎风侧主缆在气动力作用下发生运动,进一步影响自身的气动力以及下游侧主缆的气动力,进而影响到自身和下游侧主缆的运动特性。由于四主缆悬索桥建设经验比较有限,相关研究较少。早期学者大多针对刚性或弹性支撑的刚体二维模型进行试验研究或CFD(computational fluid dynamics)模拟。如Dielen等[11]通过弹簧悬挂模型风洞试验,研究了两圆柱间距比W/D0≤4(W为两圆柱中心距,D0为圆柱直径)时的气动干扰,发现尾流驰振的临界风速随Scruton数和间距比的增大而升高,且当下游圆柱发生尾流驰振时上游圆柱也会出现小幅振动。Tokoro等[12]针对不同间距串列拉索模型进行了刚性支撑风洞试验,在间距为4.3D,风攻角为15°时观测到了以一阶模态为主的尾流驰振。Sumner等[13]通过风洞试验测量了两个等径交错圆柱体在横流中的平均空气动力和涡流脱落频率。而实际中桥梁主缆为垂度效应明显的细长结构,有必要进行考虑垂度的气弹模型试验,来研究其三维状态下的相互干扰特性。Loredo-Souza等[14]开展了两条平行输电电缆在强风下的气弹模型试验,表明随着两条电缆间距增大,其阻力的相干性减小,并且随着风速的增加而减小。Li等[15]开展了平行拉索三维弹性模型风洞试验,观察到尾流驰振对攻角很敏感;偏角约为10°~20°的拉索最容易受到尾流驰振影响;当间距增加时,尾流驰振变得不那么敏感;在多个位置使用刚性连接可以抑制尾流驰振。陈政清等[16]以广东佛山平胜大桥中的无吊索两平行主缆为研究背景,在串列主缆模型试验中观测到了以一阶模态为主的尾流驰振现象,发现主缆间距风偏角及风攻角的变化对尾流驰振临界风速存在明显影响。
综上,单主缆驰振研究主要集中施工期暂态主缆,主要关注驰振临界风速及控制措施;并置双主缆风致振动研究较少,主要采用风洞模型试验手段进分析。本文建立均匀流作用下考虑主缆三维效应、主缆间气动干扰效应和双向流固耦合效应的四主缆悬索桥单侧并置双主缆振动分析方法,以广州狮子洋大桥初步设计阶段提出的单跨吊四主缆悬索桥方案为研究背景,对均匀来流作用下成桥状态中跨主缆的横向振动,以及边跨主缆的横向、竖向振动进行数值模拟,对振动特性进行了分析。
1 均匀流作用下并置双主缆振动分析方法
1.1 主缆系统运动方程
风荷载作用下桥梁结构的运动方程可表示为
(1)
式中: [M],[C]和[K]为桥梁的质量、阻尼和刚度矩阵;X为桥梁的位移向量;F为桥梁的风荷载向量。
将桥梁整体分解为两个子系统,即主缆子系统和除主缆之外的子系统,桥梁整体运动方程式(1)改写为
(2)
式中: 下标ca和ot分别为主缆子系统和除主缆之外的子系统;下标co或者oc为主缆子系统和除主缆之外的子系统之间相互影响部分。
采用振型分解法,当重点关注主缆的运动时,选择主缆的前几阶主振型来近似表达系统的位移向量。为简化推导,这里暂且以单阶振型来表达系统位移,此时桥梁运动方程可以表示为
X=φiqi
(3)
(4)
式中:φi为关于主缆的i阶主振型;qi,ωi和ξi分别为主缆i阶主振型对应的模态坐标、振动频率和阻尼比。
振型向量也分解为主缆子系统和其他子系统两部分,即
(5)
当选择以主缆为主的振型时,φi,ot相对于φi,ca部分而言可以忽略不计。由于一般情况下主缆的纵向、横向和竖向振型是相互独立的,且横风作用下纵向振动不容易发生,因此如下所示。
(1) 当φi是以主缆横向振动为主的振型时
(6)
式中:φcaH,i和FcaH为主缆横向振动自由度对应的振型和风荷载;qHi,ωHi和ξHi分别为主缆横向振动的模态坐标、振动频率和阻尼比。
(2) 当φi是以主缆竖向振动为主的振型时
(7)
式中:φcaV,i和FcaV为主缆竖向振动自由度对应的振型和风荷载;qVi,ωVi和ξVi分别为主缆竖向振动的模态坐标、振动频率和阻尼比。
1.2 主缆风荷载简化
由于主缆是三维结构,不同高度处主缆单位长度上的风荷载是不同的。为简化计算,假设不同高度处的阻力系数是相同的,则单根主缆节点j上的横向风荷载可表示为
(8)
其中
(9)
(10)
式中:zj为节点j的高程;α为风剖面指数;Lj为节点j对应的长度;D为主缆截面直径;U0,z0,CD0(t)和H0(t)分别为参考点0处的风速、高程、主缆断面阻力系数和主缆单位长度的风阻力;Cj为节点j相对于参考点0的风阻力调整系数。
主缆横向风荷载FcaH可以表示为
FcaH={H1(t)H2(t) …Hn(t)}T=
H0(t){C1C2…Cn}T=CH0(t)
(11)
与主缆横向风荷载简化过程类似,主缆竖向风荷载FcaV可以表示为
FcaV={V1(t)V2(t) …Vn(t)}T=
V0(t){C1C2…Cn}T=CV0(t)
(12)
其中
(13)
式中,CL0(t)和V0(t)分别为参考点0处的主缆断面升力系数和主缆单位长度风升力。
上述推导过程中,假设不同高度处的阻力系数是相同的,将整根三维主缆的风荷载用参考点处主缆单位长度风荷载进行表达,从而可用二维CFD模型进行求解,因此,这种处理方式相当于是将难以处理的三维问题转化为二维问题,从而降低了计算难度。当然,不同高度处的阻力系数可能并不完全相同,上述处理方式存在一定误差,如要提高计算精度,可以将主缆分为多个区段,每个区段内选择代表性参考点,每个区段的主缆风荷载用区段内代表性参考点处主缆单位长度风荷载表达。虽然这样处理可以提高精度,但是也大大增加了计算的工作量。
1.3 单侧并置双主缆简化运动方程
根据1.1节和1.2节,主缆横向和竖向振动一阶近似可以表示为
(14)
(15)
其中
(16)
(17)
以迎风侧主缆为例,在计算得到了迎风侧主缆参考位置处的主缆单位长度风升力H0f或风阻力V0f后,迎风侧主缆的模态坐标可以通过式(14)~式(17)求得,进而求得迎风侧主缆任意位置的位移,如参考点处的位移可表示为
xH0f=φcaH,i-0fqHif
(18)
xV0f=φcaV,i-0fqVif
(19)
式中:φcaH,i-0f和φcaV,i-0f分别为迎风侧主缆参考点处的第i阶振型的横向分量和竖向分量;qHif和qVif分别为迎风侧主缆的第i阶振型模态坐标。
同理,可以求得背风侧主缆的模态坐标qHir和qVir,以及参考点位置处的位移xH0r和xV0r,此处不再赘述。
1.4 多模态振动
为简化,上述推导过程中只考虑单了一阶振型振动即单模态振动,当考虑多个模态振动时,只需联立多个相互独立的方程求解各阶模态坐标即可,例如迎风侧主缆参考点处的位移可表示为
(20)
式中:φHk-0f为迎风侧主缆参考点处的第k阶振型的横向分量;qHkf为迎风侧主缆第k阶振型的模态坐标;N为计算中考虑的模态阶数。
2 均匀流作用下并置双主缆运动求解方法
2.1 并置双主缆气动干扰效应
相比单侧单主缆而言,并置双主缆由于迎风主缆和背风主缆气动干扰,在计算参考点处的单位长度风阻力H0f(t)和H0r(t),以及风升力V0f(t)和V0r(t)时,需要考虑迎风主缆、背风主缆之间的气动干扰效应。
由于迎风主缆、背风主缆之间的位置随着时间变化而变化,导致迎风主缆、背风主缆之间的气动干扰效应是随时间变化而变化的,因此,为准确地考虑迎风主缆、背风主缆之间的气动干扰效应,需要建立迎风主缆、背风主缆的双向流固耦合模型进行求解。
2.2 计算分析流程
整个计算分析流程如图1所示。分析中最主要的工作是采用CFD方法获得主缆上的流体作用力和求解结构动力学方程获得主缆的运动状态。主要计算步骤包括:
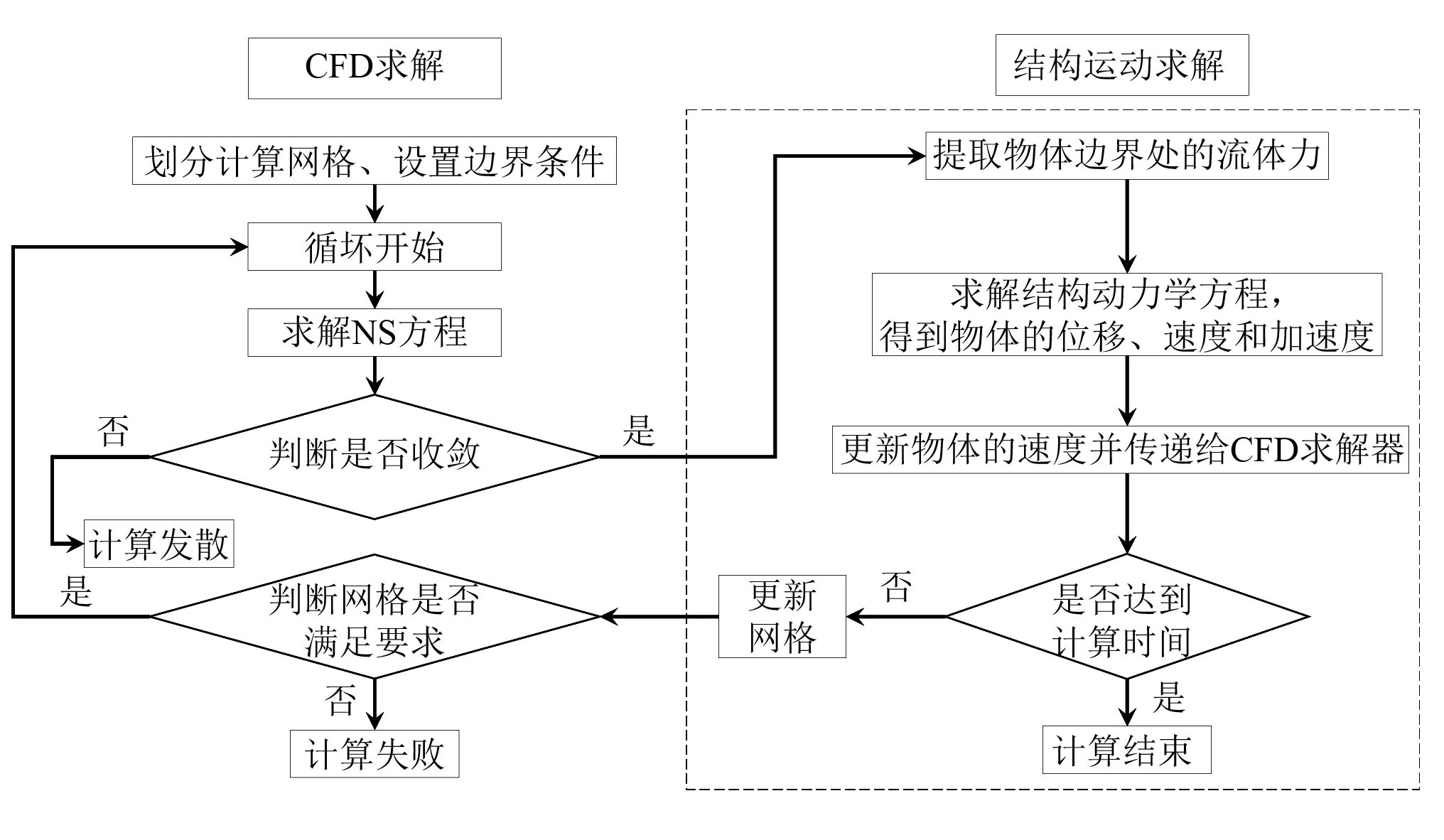
图1 计算流程Fig.1 Calculation process
步骤1划分计算域网格,设定边界类型。
步骤2根据t时刻主缆的位移,更新网格。
步骤3计算t时刻的参考点处主缆单位长度受到的风荷载H0f(t),V0f(t);H0r(t),V0r(t)。
步骤4采用龙格库塔法求解迎风侧主缆和背风侧主缆的模态坐标方程,计算t+dt时刻的模态坐标qHif,qVif,qHir和qVir,进而得到t+dt时刻参考点处主缆的运动位移xH0f,xV0f,xH0r和xV0r。
步骤5令t=t+dt,重复步骤2~步骤4,直到计算时间结束。
3 主跨2 000 m悬索桥单侧并置双主缆振动分析
3.1 桥梁方案简介
狮子洋大桥主跨2 180 m,通行16车道,在初步设计阶段,设计院提出了单侧并置双主缆分离式吊索的四主缆单跨吊悬索桥方案,主缆锁夹外直径1.0 m,中跨双主缆设计中心间距3 m,边跨双主缆设计中心间距3.0~19.5 m主缆-主梁结构效果图,如图2所示。

图2 主缆-主梁结构效果图Fig.2 Main cable-main beam structure renderings
成桥状态中跨主缆受主梁约束,主缆竖向振动与主梁竖向振动耦合,迎风主缆和背风主缆将保持同步振动。由于主梁受风作用带动迎风侧主缆和背风侧主缆的运动是相同的,本文主要研究横风作用下的双主缆横向相对运动,因此,只关注迎风侧主缆和背风侧主缆的自身振动即可。主缆一阶横向振动频率为0.163 8 Hz,振型如图3所示。

图3 中跨主缆横向一阶振型Fig.3 Transverse first-order mode shape of mid-span main cable
成桥状态边跨主缆不受主梁约束,主缆振动表现为横向振动和竖向振动。本文对横风作用下的主梁横向振动和竖向振动进行同步模拟。边跨主缆一阶横向振动频率0.193 9 Hz,一阶竖向振动频率0.201 5 Hz,相应的一阶横向和竖向振型如图4和图5所示。

图4 边跨主缆横向一阶振型Fig.4 Transverse first-order mode shape of side span main cable

图5 边跨主缆竖向一阶振型Fig.5 Vertical first-order mode shape of side span main cable
3.2 成桥状态中跨主缆
采用RANS 方程和RNGk-ε湍流模型模拟流场,模型计算域及边界条件示意图,如图6所示。主缆直径D=1.0 m,计算域横向尺寸为20D,竖向尺寸为10D,两主缆中心间距为3D,两主缆间距中点位于计算域的中心位置。入口为速度入口,出口为压力出口,两侧为对称边界,主缆为壁面边界。

图6 中跨主缆流固耦合计算域及边界条件示意图Fig.6 Schematic diagram of the fluid-structure coupling calculation domain and boundary conditions of the mid-span main cable
针对均匀风速3.5~42.0 m/s(桥址处10 m高10 min平均风速,下同)作用下中跨主缆振动进行模拟。主缆阻尼比假设为5‰。
部分风速下迎风侧、背风侧主缆风致振动位移响应时程,如图7所示。从计算结果可以看出:①主缆振动主要表现为简谐振动;②迎风侧、背风侧主缆的振动频率基本相同;③迎风侧、背风侧主缆的振动幅值不同;④迎风侧、背风侧主缆振动存在相位差。
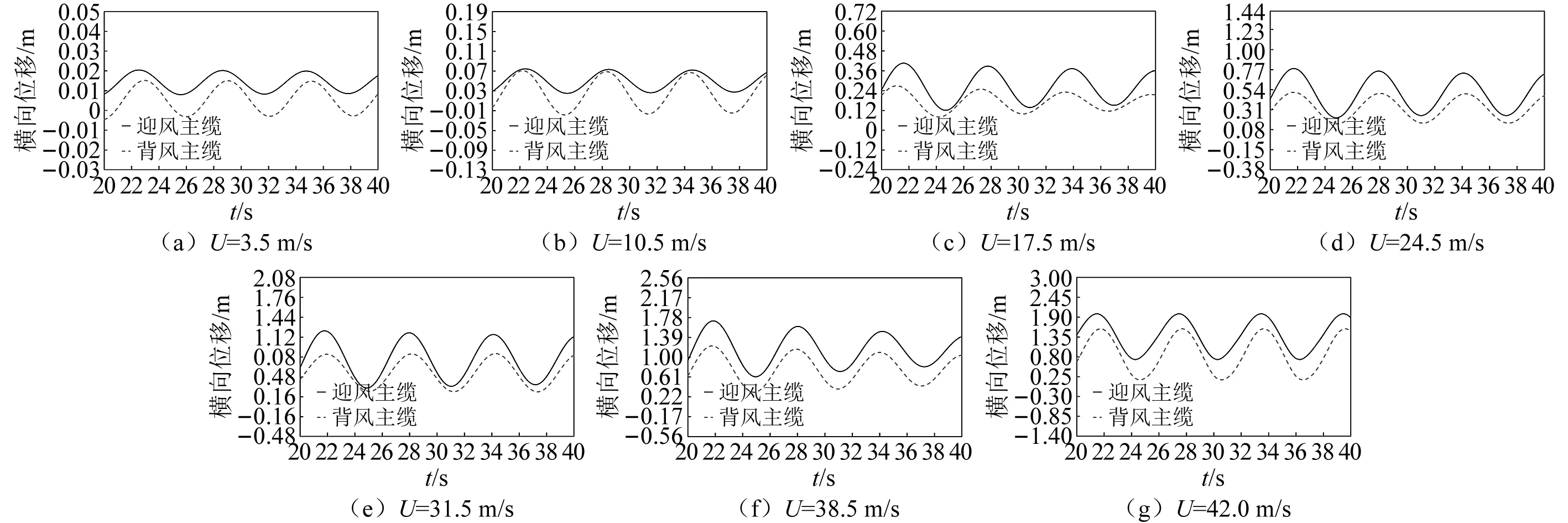
图7 不同风速下中跨并置双主缆的振动位移时程Fig.7 Vibration displacement time history of mid-span juxtaposed double main cables under different wind speeds
迎风侧、背风侧主缆运动幅值随风速变化情况,如图8所示。由图8可知:①迎风侧、背风侧主缆振动平均值、最大值随风速增大而增大;②迎风侧、背风侧主缆的振动幅值随风速非线性变化,当风速为42.0 m/s时,最大振幅接近0.7 m。
随着风速增加,迎风侧、背风侧主缆的中心间距减小,当风速为42.0 m/s时,最小间距为1.9 m,大于并置双主缆接触时的最小中心间距1.0 m,表明两主缆不会发生接触。
3.3 成桥状态边跨主缆
设计方案中边跨主缆中心距是变化的,本研究中假设主缆按等间距3 m布置,这样分析结果将是偏安全的。由于边跨主缆竖向无主梁约束,迎风侧、背风侧主缆的气动干扰现象将更加明显,尾流驰振发生概率大。在CFD模型中,考虑风攻角影响。风攻角α定义为风的主流方向与两主缆中心连线之间的夹角,其中背风侧主缆中心在与迎风侧主缆中心连线的下方时,风攻角为正,反之风攻角为负,如图9所示。对边跨主缆横向和竖向振动进行模拟,主缆阻尼比假设为5‰。
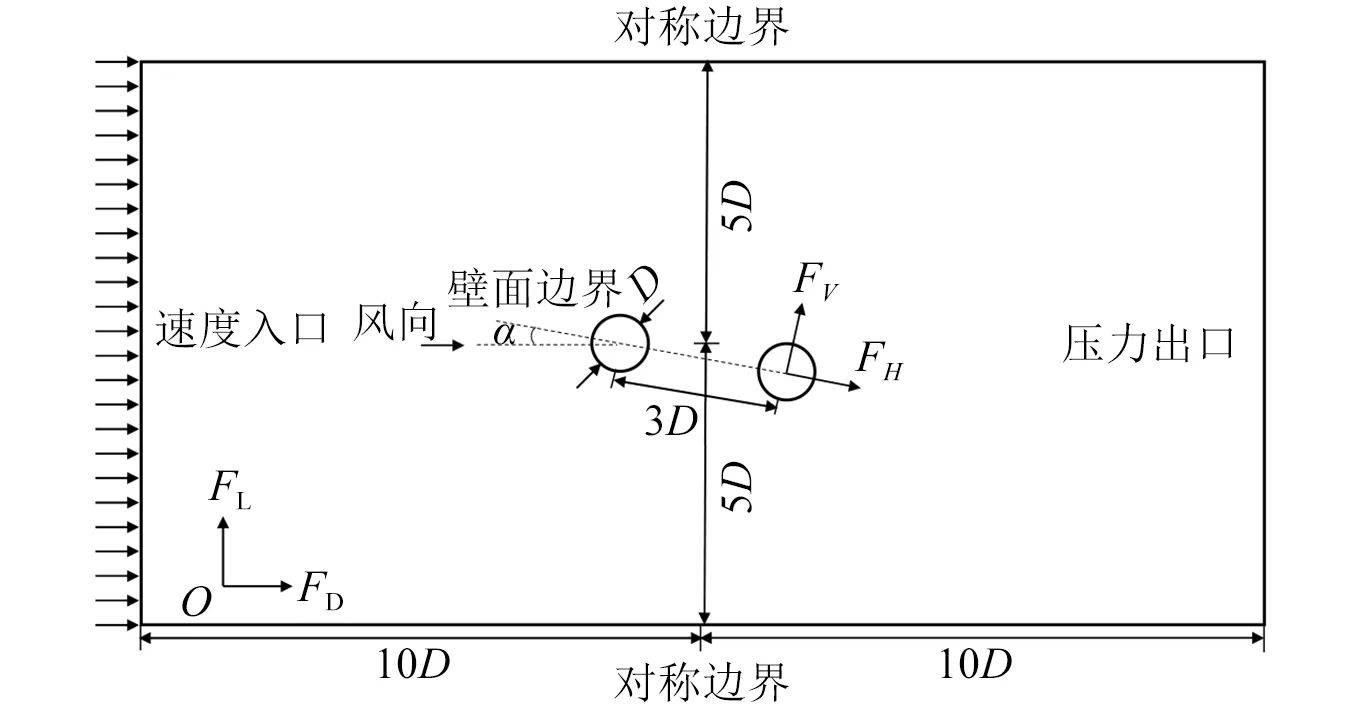
图9 边跨主缆流固耦合计算域及边界条件示意图Fig.9 Schematic diagram of fluid-structure coupling calculation domain and boundary conditions of side span main cable
对-3°~3°间隔1°共7个风攻角及21 m/s和41.5 m/s两个风速作用下的边跨并置双主缆振动进行模拟。结果显示,除了风攻角0°工况外,其他工况下的主缆振动无明显发散现象。针对风攻角0°工况,进一步补充计算了26 m/s,31.5 m/s和38.5 m/s共3个风速工况的振动响应。当风攻角为0°时不同风速作用下的主缆振动时程如图10所示。主缆振动幅值如图11所示。风速38.5 m/s工况下不同时刻边跨双主缆周围风速矢量,如图12所示。由图10可知:当风速为26 m/s时,背风侧主缆竖向位移幅值随时间周期性变化,表现出类似于“拍”的振动现象,但最大振幅出现在前100 s;当风速为41.5 m/s时,背风侧主缆竖向位移幅值随时间逐渐增大后减小最终趋于稳定;其他风速工况时背风侧主缆竖向位移幅值随时间逐渐增大最终趋于稳定。由图11可知,随着风速的增加,主缆振动幅值先逐渐增大,一定风速后幅值有所减小。迎风侧主缆竖向位移幅值随时间变化非常小,随风速变化的趋势与背风侧主缆相似,但幅值比背风侧主缆小得多。从上述结果表明,当风攻角为0°时,边跨背风侧主缆存在尾流驰振现象。
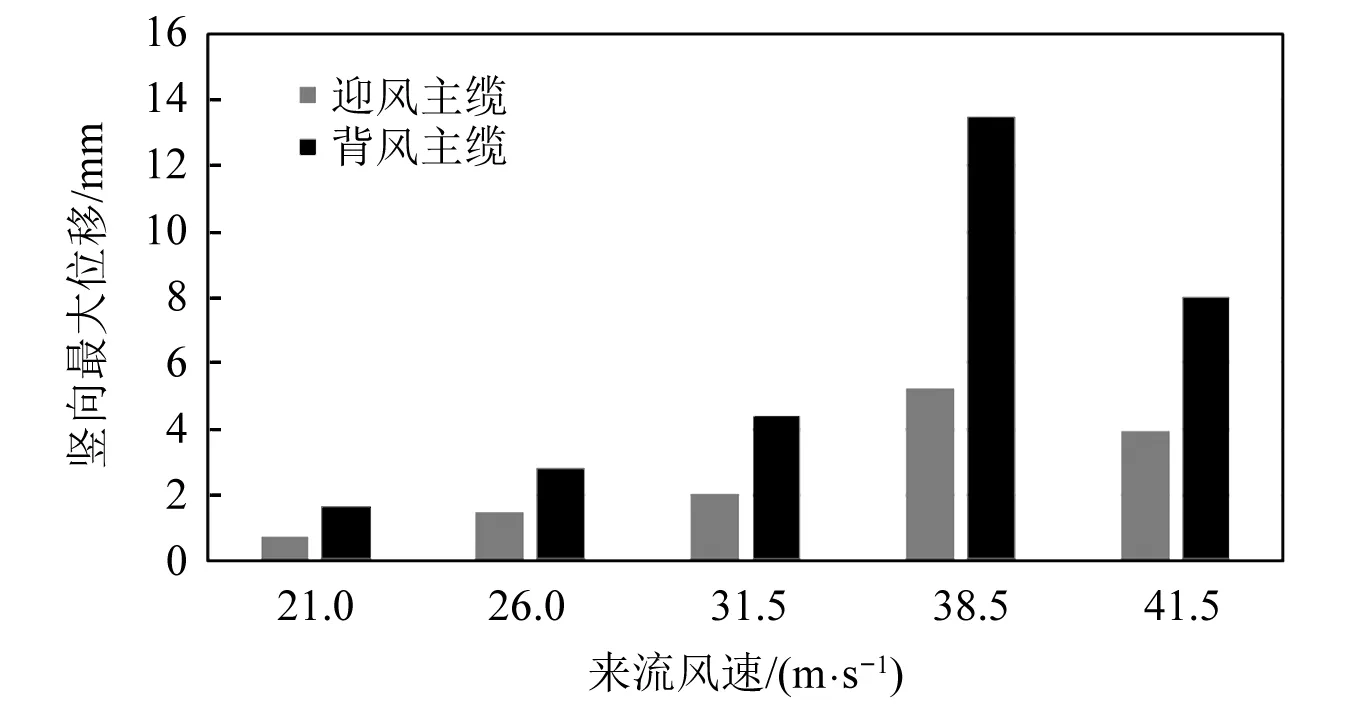
图11 不同风速下边跨主缆振动幅值Fig.11 Vibration amplitude of side span main cable under different wind speeds

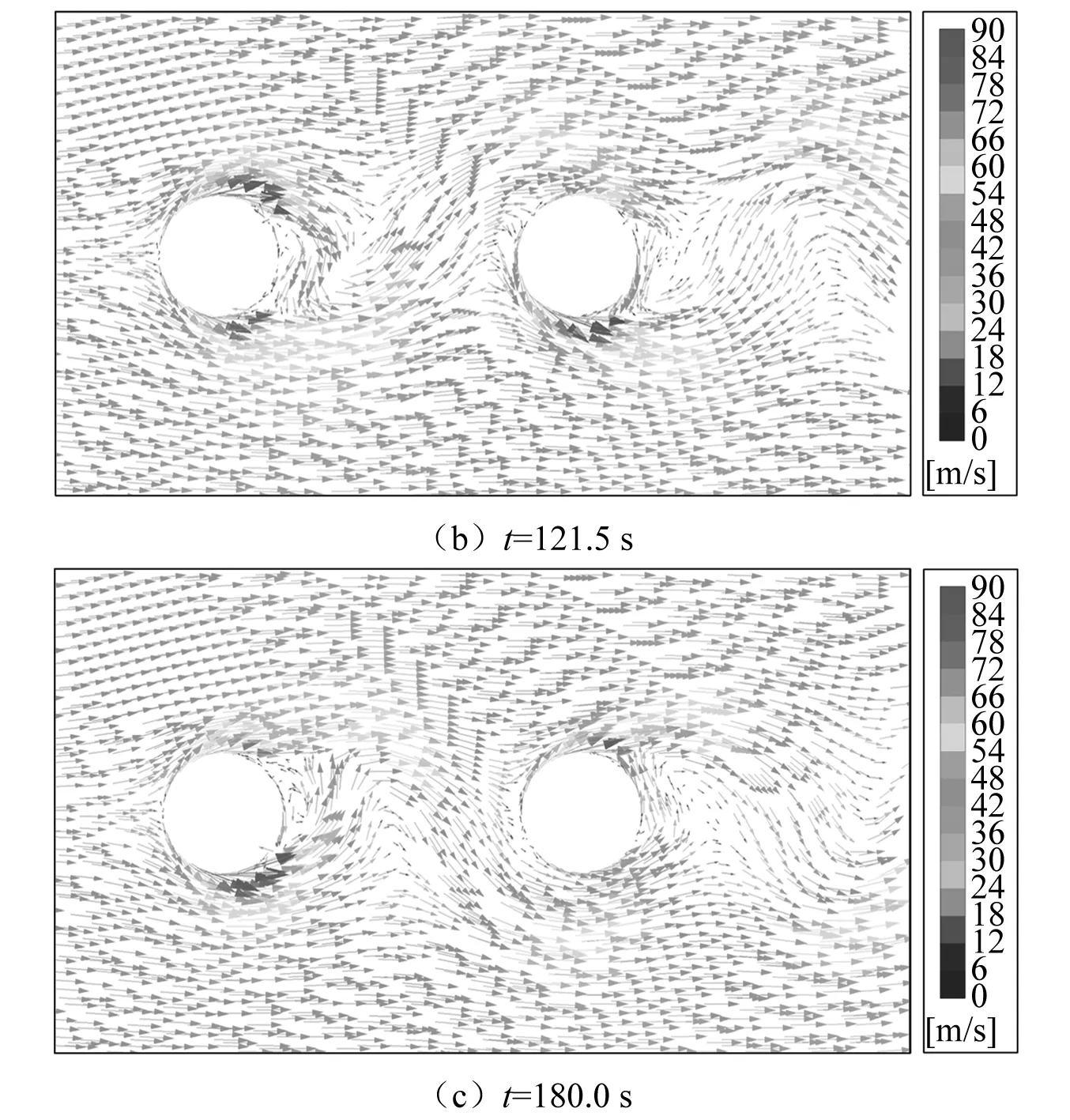
图12 不同时刻边跨双主缆周围风速矢量图(U=38.5 m/s)Fig.12 Vector diagram of wind speed around the side span main cable at different time
边跨背风主缆在常遇风速和高风速均匀流作用下都有可能发生尾流驰振。因此,如果采用四主缆方案,建议采用螺旋式、凹坑等抗风气动控制措施对边跨主缆进行处理,并采用风洞模型试验对抗风措施的效果进行确认。
4 结 论
(1) 建立了均匀流作用下考虑主缆三维效应、主缆间气动干扰效应和双向流固耦合效应的四主缆悬索桥单侧并置双主缆振动分析方法。该方法将桥梁系统分解为主缆子系统和除主缆之外的子系统,采用振型分解法用主缆前几阶横向和竖向振型近似表达主缆子系统的位移,建立模态坐标下主缆的运动方程,将不同高度处主缆气动力用代表性位置主缆气动力近似表达,采用流固耦合模型计算均匀流作用下代表性位置主缆气动力,通过结构运动方程和流体动力学方程的双向迭代求解最终获得主缆子系统模态坐标和主缆的振动位移。
(2) 均匀流作用下主跨2 180 m四主缆单跨吊悬索桥成桥状态中跨主缆的振动分析结果表明:不同风速作用下,中跨迎风主缆、背风主缆的振动频率基本相当,但存在一定相位差;随着风速增加,双主缆之间的中心间距不断减小,但最不利情况下(风速42.0 m/s),双主缆间的中心间距远大于双主缆接触时的最小净矩,双主缆间不会发生接触。
(3) 均匀流作用下主跨2 180 m四主缆单跨吊悬索桥边跨主缆的振动分析结果表明:特定风攻角下,边跨背风主缆存在尾流驰振现象,建议采用螺旋式、凹坑等抗风控制措施对边跨主缆进行处理。

