基于支持度和确定度的异构数据融合方法*

项新建，李可晗，曹 楹，黄炳强，郑永平

(浙江科技学院自动化与电气工程学院，浙江 杭州 310023)

随着信息技术的不断发展，单一传感器采集的信息已经不能满足农业、工业和军事等领域的需要，与单感器相比，多传感器数据有更高的参考价值。由于多传感器系统采集的数据可能会存在一定的不确定性和矛盾性，因此怎样更好地处理多传感器数据，进一步提高数据融合结果的可靠性，是目前数据融合技术领域的热门研究方向。

Dempster-Shafer(D-S)证据理论作为一种数据融合算法，能够很好地处理“不确定”和“不知道”的问题，被广泛运用于目标识别、故障分析和多属性决策分析等领域[1]。 然而其在处理冲突证据时，容易产生与事实相悖的结论。 目前，对于D-S 证据理论的改进主要分为两个方面:对组合规则的改进[2-4]以及对证据体的改进[5-13]。 前者把产生与事实相悖的结果归责于D-S 规则本身，虽然取得了一定的效果，但破坏了D-S 规则本身的优势，而后者在保留Dempster 规则优良特性的同时弱化了冲突证据对融合结果的影响，因此在实际应用中，对证据体的改进从各方面上看都更为合理[5]。

对证据体的改进方法可分为两大类:折扣系数法和加权平均法。 以胡昌华[6]为代表的学者提出折扣系数法，根据证据间的相互距离确定证据权重，并修正证据，将不确定的部分分配给全集，虽能提高结果可靠性，但是会影响收敛速度和聚集效果[7]。 以Murphy[8]和Deng[9]为代表的学者提出加权平均法，对证据进行加权平均处理后进行融合，有更好的融合效果，因此本文采用加权平均法处理证据。 然而Murphy[8]利用简单平均法给每个证据赋予相同的权重，Deng[9]依据信任度确定证据权重，二者均充分利用证据信息。 确定证据体权重的方法有两种:根据证据自身特性和根据证据间的关系，且目前尚未存在统一确定证据权重的方法。 前者又可分为两类:一是基于信息熵，虽能在一定程度上描述证据自身的特性，然而使用该类方法处理证据的方式较为片面，仅用证据部分信息代替了整个不确定区间[10]；二是区间距离，如赵静等[10]提出利用定积分区间距离来衡量证据的不确定性，但是计算较为复杂，Deng 等[11]提出一种基于证据置信区间的海林格距离衡量证据不确定度的方法，能够较好地度量证据自身特性，从而达到较好的融合效果。 对于后者，在单一关系测度无法准确测量证据间关系的情况下[12]，多数学者提出利用多关系测度衡量证据间关系的方法，如王路等[12]结合余弦相似度和Jaccard 系数衡量了证据间关系，然而这两个测度均为相似性测度，对证据间关系的分析不够全面，许将军等[13]基于证据间的相似度以及冲突系数定义了新的证据冲突度，然而其并没有考虑到证据单焦元和多焦元的关系。

为了充分挖掘异构多传感器数据信息，解决多传感器数据存在冲突性等问题，提高数据融合的准确率，本文提出一种基于证据支持度和确定度的证据理论融合方法。 首先，结合Jaccard 系数改进冲突系数K和余弦相似度，并结合二者计算证据间支持度，第一次修正证据；其次，利用修正后证据焦元区间的兰氏距离衡量证据的自身确定度；最后，基于确定度与支持度生成证据总权重，加权平均处理证据后，按Dempster 规则进行融合。 本文通过算例和应用证明了所提方法的有效性。

1 相关理论知识

定义1在D-S 证据理论内，设Θ＝θ1，θ2，…，θn为有限识别框架，基本信任函数m是从集合2Θ→[0，1]的映射，A为Θ的任一子集，满足:

称m为Θ的基本概率分配函数(简称BPA 函数)[14]，若m(A)＞0，则称A为识别框架Θ内的一个焦元，m(A)反映了证据对A的信任程度。

定义2设Θ为识别框架，m为其BPA 函数，则

称Bel(A)为信任函数，为A全部子集的基本概率分配之和，表示命题A的确定度。

称Pl(A)为似然函数，表示不否认A的信任度。 称[0，Bel(A)]为命题A的支持区间，[Bel(A)，Pl(A)]为命题为A的置信区间，[Pl(A)，1]为证据的拒绝区间。 其中支持区间和拒绝区间共同构成证据的确定区间，可表示证据的确定度。 证据的各区间如图1 所示。

图1 证据区间图

定义3设m1，m2为同一有限识别框架Θ上的2 个BPA 函数，则定义m1和m2的Dempster 组合规则为:

式中:K为证据m1和m2冲突系数，其值越大，证据间的冲突程度越大。

2 基于确定度和支持度的证据融合方法

本文在上述理论的基础上，提出一种基于证据确定度和支持度的证据加权方法，提高融合结果的准确性。

2.1 证据支持度

根据式(5)，可以得出D-S 规则定义下的冲突系数K，然而在一定的情况下，该系数并不能正确地表示证据间的冲突度，比如当两个证据完全相同时，有:

可算出冲突系数K为0.80，表明两个数据存在高度冲突，该结论与事实相悖。

Xu 等[13]提出结合冲突系数K和余弦相似度衡量证据全局冲突度的方法，然而该方法在衡量多焦元证据体时，会出现不够准确的情况，降低融合结果的准确性。 如有证据m1和m2:

分别利用冲突系数K和Xu 等[13]所提的方法计算证据m1和m2的冲突度，得到的结果均为0，表明证据完全相似。 然而由于无法判断证据m2对各焦元的支持度，因此两个证据存在一定的冲突，因此冲突系数K和Xu 等[13]方法所计算的冲突度均与事实不符。

结合上述分析，冲突系数K在度量相同证据和多焦元证据时，均会出现失效的情况，且余弦相似度同样不能准确度量多焦元证据之间的关系[12]。Jaccard系数可用于比较两个样本之间的差异性和相似性，其值越高，则两个样本相似度越高[15]。 因此，本文提出使用Jaccard 系数改进冲突系数K和余弦相似度的方法，并结合改进后的余弦相似度和冲突系数共同度量证据之间的关系，提高融合结果的可靠性。

定义4假设有证据mi和mj，识别框架Θ＝θ1，θ2，…，θn，定义证据局部相似度为s′ij，局部冲突度为Kij:

结合所计算的局部相似度和局部冲突度，可得证据的局部支持度sij，从而得到证据基于支持度的权重αi:

2.2 证据确定度

可基于证据焦元的区间距离衡量证据自身的特性，如证据的置信区间距离越长，代表不确定信息越多，对应的证据不确定性也越大。 兰氏距离常被用于确定样本间距离，因其适合大规模处理数据，且对于接近于0(大于等于0)的值的变化非常敏感，本文提出结合证据支持区间和拒绝区间的兰氏距离衡量证据确定度的方法。

假设X＝{x1，x2，…xn}，Y＝{y1，y2，…yn}是随机变量Z的两个概率分布向量，则其兰氏距离为:

定义5假设识别框架Θ＝A1，A2，…，An，定义DU(mi)为证据确定度，计算方法如下:

将所求得的确定度DU(mi)归一化处理后可得证据基于确定度的权重:

2.3 所提方法步骤

证据的确定度是从证据自身出发，用来反映证据自身可信程度，证据的确定度越高，对应的权值也越高；证据的支持度衡量了证据之间的冲突关系，支持度越高，表示证据在证据群中的可信度越高。 证据自身的确定度和证据间的支持度互不影响，且都是证据内可获取的有效信息。 仅考虑其中之一处理证据，都将破坏证据信息的完整性，因此，考虑证据确定度和支持度来修正证据的方式更合理。

随着国家“健康中国”战略的实施，健康管理已经上升到非常重要的高度。对于从事健康管理的人员而言，如何正确认识健康管理的核心内涵及在实践中成功的实施至关重要。这就需要我们深入地思考健康管理的合理化模式，并在实践中不断地加以修正。

综上所述，给出本文所提方法的具体步骤:

Step 1 结合式(6)和式(7)，计算出基于证据支持度的权重αi(αi的取值范围为[0，1])，根据权重αi对数据按修正公式(11)进行第一次修正。

Step 2 计算修正后的各证据体的信任函数和似然函数，按照式(9)和式(10)计算出基于证据确定度的权重βi。

Step 3 根据权重αi和βi，计算出证据体的总权重，将其归一化后得到最终权重ωi，具体计算方式如下:

Step 4 依据权重ωi，对原证据进行加权融合:

Step 5:按照D-S 证据理论融合规则，对融合后的证据体m进行n-1 次融合。

3 算例结果分析

本节分别从冲突证据融合、多数量证据融合和正常证据融合三个方面分析验证所提方法的有效性。

3.1 冲突证据融合

证据理论内共有四种常见的冲突种类:完全冲突、0 信任冲突、1 信任冲突和高冲突[16]，四种常见冲突的BPA 函数如表1 所示。 利用本文所提融合方法分别对表1 内常见冲突证据体进行融合，对比传统证据理论及经典改进方法，融合结果如表2所示。

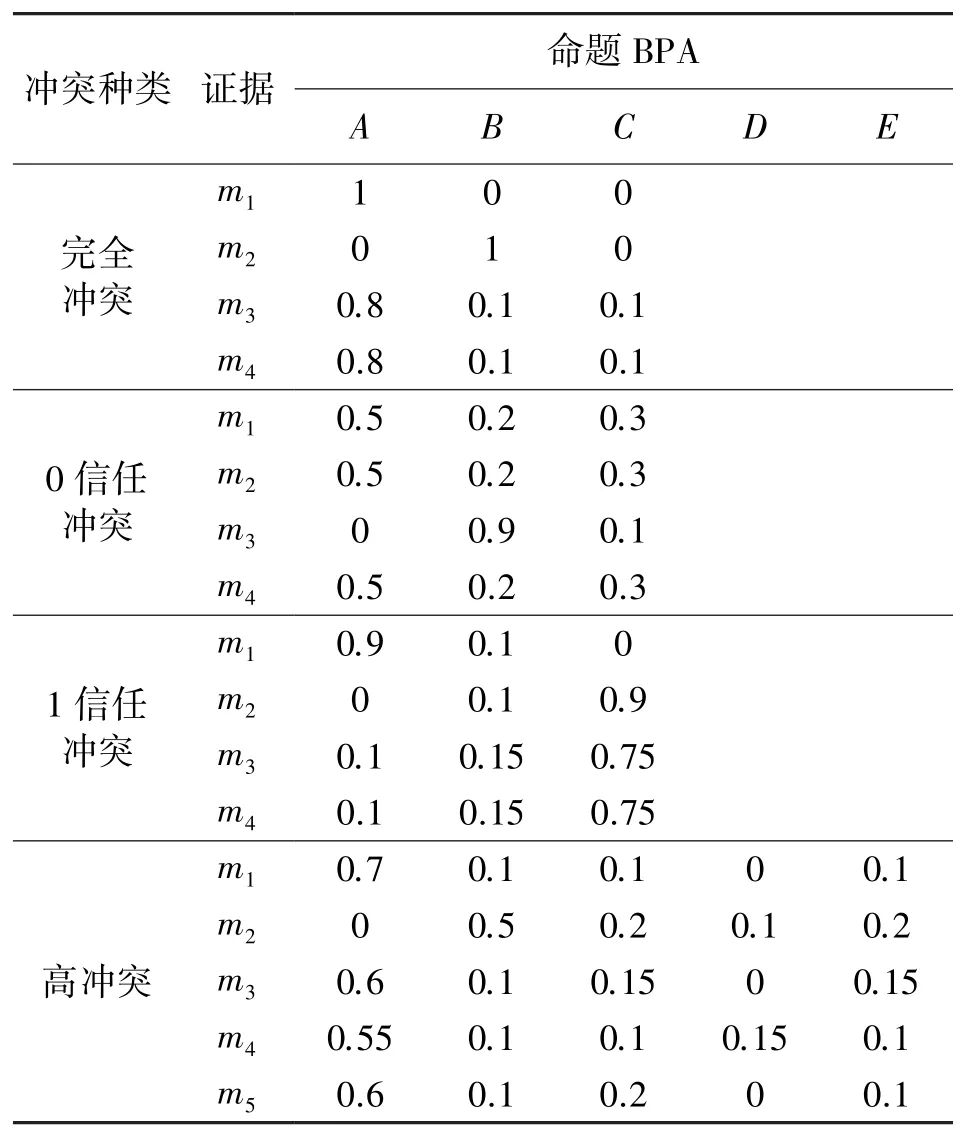
表1 四种常见冲突BPA 函数

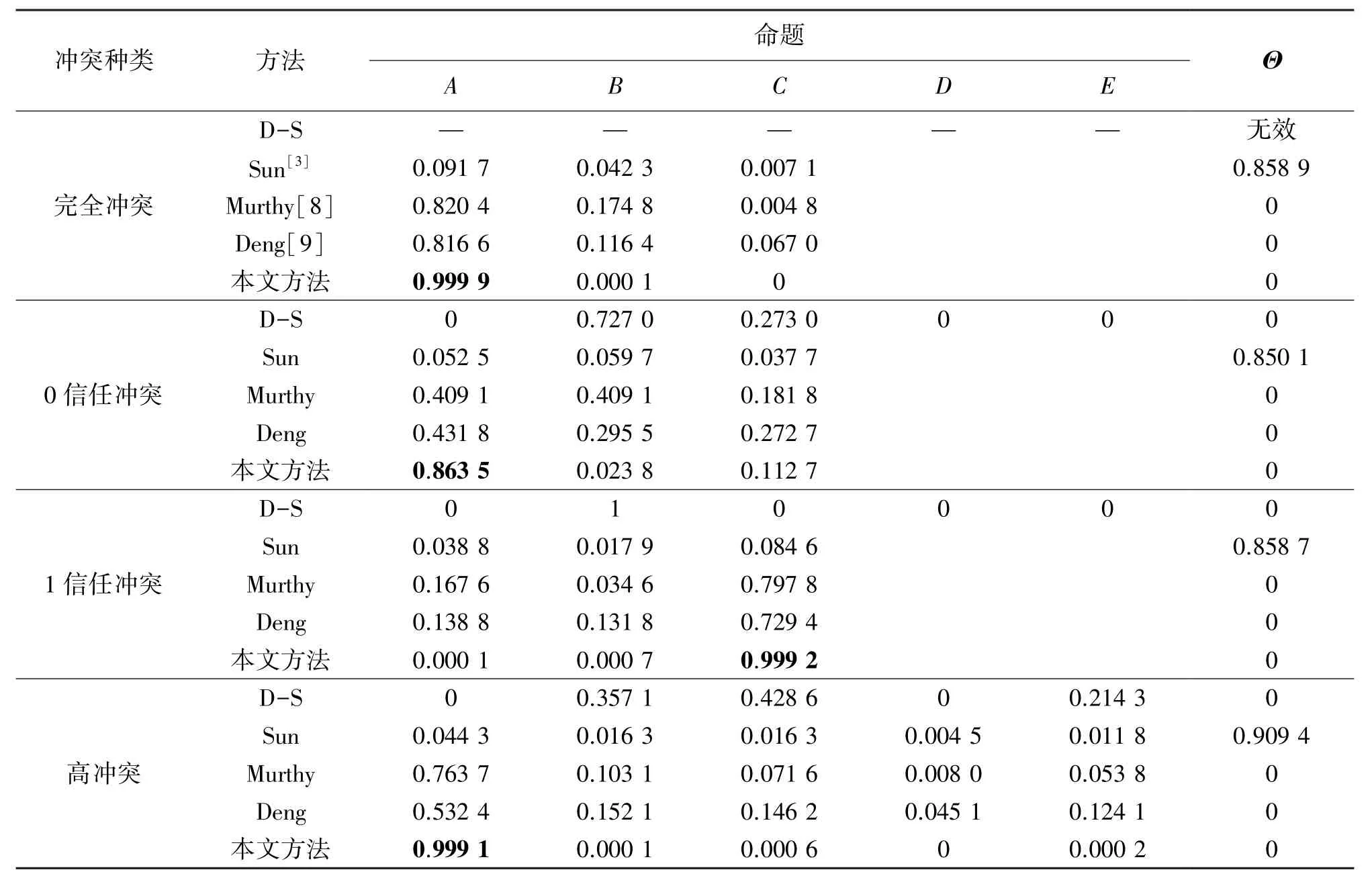
表2 四种常见冲突的融合结果

3.2 多数量证据融合

由于王路等[12]提出了一种结合信任度和确定度的方法，本文所提方法在许将军等[13]所提出的冲突度计算方法上进行了改进，且借鉴了Deng 等[11]利用证据焦元区间距离衡量的思想，因此本文将上述三种方法作为相似方法。 表3、表4 分别为多数量单、多焦元冲突证据体的BPA 值分布。

表3 单焦元证据分布

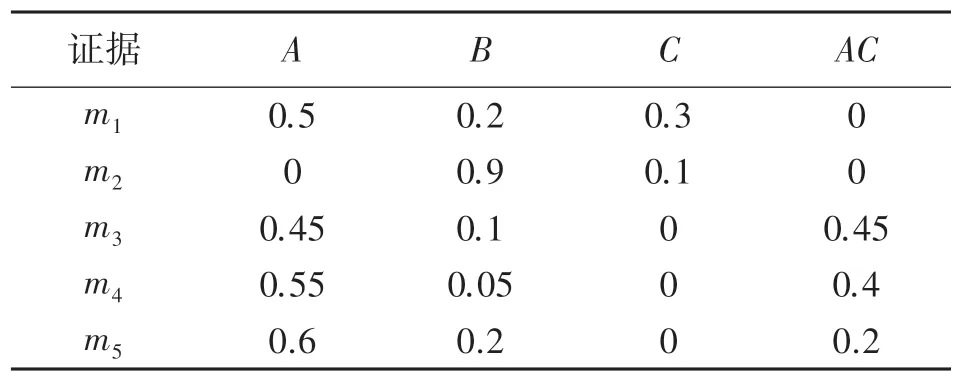
表4 多焦元证据体数据分布

不同数量下的单、多焦元证据权重图如图2、图3 所示。 从图2、图3 可以看出，处理不同的单、多焦元证据时，王路[12]、许将军[13]和本文所提方法均降低了冲突证据的权重，而本文所提方法的冲突证据权重更小，说明了该方法处理冲突证据时有更优异的性能，证明了其有效性。 由于Deng[11]的方法衡量的是证据自身的不确定度，与证据之间的关系无关，因此该方法并没有降低冲突证据的权重。

图2 单焦元证据权重图

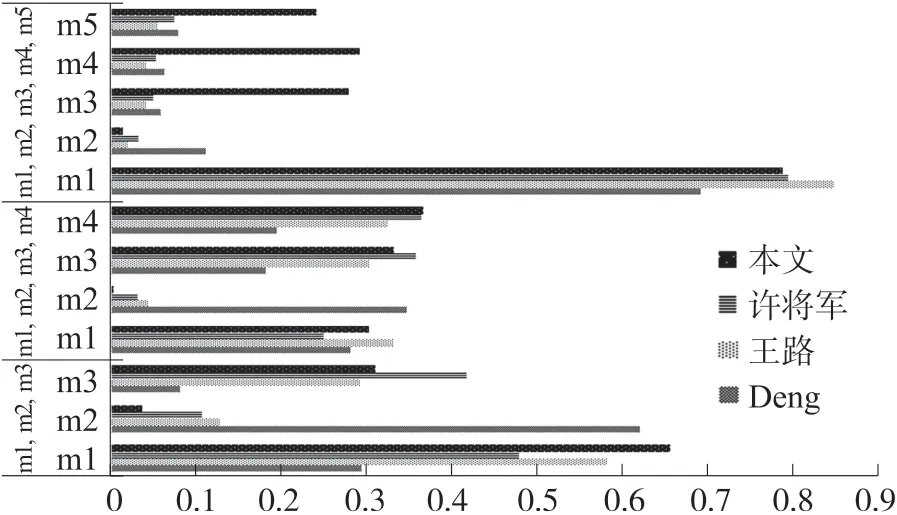
图3 多焦元证据权重图

各方法的融合结果如表5～表6 所示，从融合结果和对比结果可以看出:面对不同数量下单、多焦元冲突证据体，传统证据理论融合结果均与事实相悖。对于不同数量的证据体融合，虽然Deng、王路和许将军和本文方法均指向正确结果，但本文方法有更高的BPA 函数，且收敛速度更快。

表5 单焦元冲突数据融合结果

表6 多焦元冲突证据体融合结果

3.3 正常证据融合

表7 为正常证据体数据分布，表8 为融合结果。从表8 可以看出，面对正常不冲突的证据体，本文所提方法同样能得到正确结果，并且对比传统的证据理论算法，有更高的BPA 函数，可信度更高。

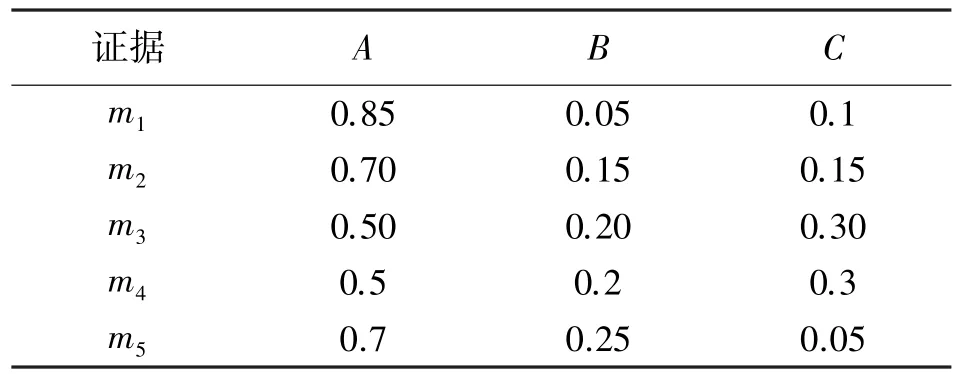
表7 正常证据体数据分布

表8 正常证据体融合结果

综上所述，本文所提的证据融合方法在处理正常证据和冲突证据时，较传统证据理论、经典改进方法和相似改进方法，均有更好的融合性能。

4 应用

将本文所提的方法应用于雷达目标识别领域，对比传统证据理论与相似改进方法，证明该方法的有效性。

雷达识别库中有3 个雷达型号数据，分别为A，B，C，设识别框架Θ＝{A，B，C}，现有五个异构传感器分别对某一雷达辐射源进行识别，结果见表9[17]。

表9 雷达识别BPA 值

根据式(6)和式(7)，计算出各证据基于支持度权重αi:

利用αi，按式(11)对证据进行第一次修正，修正后按式(9)、式(10)计算基于证据焦元区间距离计算确定度DU(mi)和基于确定度的权重βi:

根据式(12)，可算出证据的整体权重ωi:

使用权重ωi对原证据进行加权处理，得到证据m，按D-S 组合规则进行n-1 次融合，所得结果与Deng[11]、王路[12]、许将军[13]和刘康[17]方法的结果进行对比，如表10 所示。

表10 雷达识别结果表

从计算所得的相关参数可以看出，本文所提的方法大大降低了冲突证据的权重。 根据各方法融合结果可得，传统证据理论在雷达识别过程中出现与事实相悖的结果。 随着证据数量的改变，所提方法的融合结果均保持不变，都指向正确命题雷达A。虽然Deng、许将军、王路和刘康的方法均指向正确的结果，但是本文所提方法有更高的BPA 函数，对结果为雷达A的置信度更高，验证了其处理冲突证据的有效性。

5 结束语

为更好地处理多传感器系统采集数据的不确定性和冲突性，提高数据融合的准确率，提出一种基于支持度和确定度的异构数据融合方法。 把多传感器内各类数据看作不同的证据，结合改进后的冲突系数和余弦相似度确定证据支持度，并第一次修正证据。 利用修正后焦元区间的兰氏距离衡量证据确定度，并基于支持度和确定度得到证据总权重加权处理证据，最后用D-S 规则进行融合。 通过算例和应用结果证明，所提方法面对冲突证据和正常证据均能得到正确结果，并且该方法对比传统证据理论、经典改进方法和相似改进方法，均能得到更高的BPA函数，提高了融合准确率，有更好地解决冲突和聚焦能力，证明其有效性和稳定性，为多传感器数据融合提供了一定的参考价值。 如何结合同构和异构数据融合方法，共同构成完整的多传感器数据融合方法，有待进一步研究。