信号波动牵引下指纹清晰度扩库定位算法*

韦 杰，秦宁宁

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

基于位置服务(Location Based Service，LBS)是根据移动终端用户的位置信息，提供以位置为引导或附加增值的综合性和功能化的服务。 在室外环境下，全球卫星导航系统(Global Position System，GPS)能为用户提供精确的经纬信息，但由于建筑遮挡、信道多径的重叠干扰，在室内条件下GPS 无法准确测距定位，因此对于室内定位技术进行探索研究的价值日渐凸显。 大量涌现的室内定位[1]成果，虽然为LBS 在理论上提供了技术可行性支撑，但对于其普及性的开展，依然要面临着信号获取成本庞大、损耗误差波动广、信息建库代价高昂的困难。

定位技术的更新，正是基于发现问题激励下的解决问题。 考虑到室内普遍存在的WIFI 信号，其易获得、传播远、分布广的特征，使得以WIFI 信息为基础的指纹定位技术[2]，成为室内定位研究的重点方向。 而如何在减少室内定位离线阶段指纹库部署的人力与时间成本的同时，兼顾在线阶段的定位精度，是实现将LBS 融入日常应用的核心关键之一[3]。

目前，降低指纹库部署成本投入的主流方法，是根据少量已采样参考点插值模拟目标区域内大量的未采样参考点，常见的几何插值、统计建模、理论建模等方法，均可实现在小采样条件下，对全局参考点的样本扩充。 以插值点与样本点间的距离为权重的几何插值法，过程虽然简便，但以线性距离表征接收信号强度(Receive Signal Strength，RSS)的非线性属性的方式，势必会降低插值精度。 因此，为重现信号空间分布特征[4]，以克里金算法作为理论基础的统计建模法，根据插值点RSS 的最小方差及无偏估计定义样本权重，通过选择合适的变异函数重塑采样点的物理空间距离和信号空间距离的关系，实现高精度插值[5]。 但这种默认了区域内信号具有相同期望和方差的理想化假设，一定程度上降低了实用性。 因此文献[6]通过加入漂移函数，试图解决RSS 信号在区域内变异性的差异问题，但对于类似走廊、异构角落等非规则空间，RSS 协方差与参考点间欧氏距离不满足单一映射关系，克里金的各向同性假设并不适用。 文献[7]通过克里金算法进行数据库扩充后，引入离群点探测剔除误匹配参考点，提升建库效率和定位精度。

理论建模法从WIFI 信号特性本身对其空间分布进行建模预测。 无线电信号衰落特性推导出的对数传播模型在视距空间内具有较小的预测误差，而非视距的多墙体房间内K-M 传播模型的精确度更高[8]。 除空间结构影响外，不同频率的WIFI 信号同样会对模型的路径损耗指数产生不确定影响[9]。可见，复杂室内场景下，仅靠单一室内传播模型，几乎无法精确复现区域内信号分布的完整态势。 而可能存在的漂移节点或者恶意节点[10]，加剧了信号预测的失真，针对可移动节点的筛选有效提高了定位精度。 文献[11]将马尔可夫蒙特卡洛抽样方法构建到信号传播模型中，运用随机抽样解决估计问题，算法有较高精度和较低的复杂度。

为弥补插值算法在目前室内环境应用存在的场景适用泛化薄弱，插值后精度提升受限的遗憾，给出信号波动牵引下的指纹清晰度扩库定位算法(Database expansion and Indoor Localization based on Fingerprint Definition obtained by Signal-fluctuation，DIFS)。 通过对已采样参考点进行指纹清晰度识别，将二维平面上的采样参考点泛化至三维空间，以参考点间信号变化与空间位置相关性对已采样参考点进行聚类分区，拟合已采样参考点处的路径损耗指数，构建出贴合场景的差值信号传播模型实现近邻插值。 通过在线匹配测试点与参考点的清晰度，筛选参与定位的优质参考点，以高适应性插值指纹库，支撑高精度定位结果，实现离线成本降低与在线位置匹配提高的双向增益。 与现有方法相比，所提算法考虑了不同区域的信号波动特性，拥有更小的信号拟合误差、同场景下更高的定位精确度。

1 系统模型及变量描述

在平面目标空间内，布置N个无线接入点(Access Point，AP)，表示为AP ＝{APi｜1≤i≤N}，以及R个已采样参考点(Sample Reference Point，SRP)，表示为SRP ＝{SRPr｜1≤r≤R}，Z个待插值参考点(Interpolated Reference Point，IRP)，表示为IRP ＝{IRPz｜1≤z≤Z}。 SRP 和IRP 共同组成M个参考点(Reference Point，RP)，表示为RP ＝{RPj｜1≤j≤M}。 无特殊说明，算法所述必要参数描述如下:

②X＝{()｜1≤j≤M}表示RP 的空间位置集合，其中()表示RPj的二维平面坐标，关联定义XS＝{()｜1≤r≤R}表示SRPr的二维平面坐标；Y＝{()｜1≤i≤N}表示AP的空间位置集合，其中()表示APi的二维平面坐标。

③L＝(，，…，)表示在线阶段所测量到待定位目标的RSS 向量。

2 数据预处理

无线信号在环形走廊等多结构室内隔断环境中，多径、阴影干扰会出现叠加和重复等多样变化，使用传统的高斯分布拟合RSS 在简化研究的同时，会带来较大的数据偏差。

在给定单位时间T内，SRPr采集来自APi的H次信号srssir＝{srssirh｜1≤h≤H}。 对于可能出现的Q个互异RSS 取值样本，存在SRPr关于RSS 的概率分布集合Pir＝{pir1，pir2，…，pirQ}，其平均值和中位数分别为μr和δr。

鉴于信号分布特征能更多地反映出随机信号的普适特点，以RSS 集合的概率分布为尺度，可以区分化描述多样性环境下信号的真实特征，降低个别野值信号对整体匹配的干扰。 对于高频和稳定出现的信号，以其特征分布替代原始个体的离散概率描述，可以一定程度上过滤掉低频和不稳定信号。

对于随机信号而言，若在SRPr处信号稳定，则来自APi的RSS 数值上波动微弱且取值聚集，在概率上会体现为srssir的部分信号值呈高频次的稳定出现，拉高概率分布均值，数据上体现为μr≥δr。 因此不失一般性认为，当前高频信号可以代表SRPr信号。 反之，若SRPr处信号具有较高的随机性，则RSS 数值呈自然发散分布，srssir中各信号值呈现去中心化。 此时各信号值对于SRPr的原始信号具有相近的预测价值，更适合以总体信号值均值代表SRPr信号。 因此，基于信号的聚集程度和出现频次，可重新描述SRPr处来自APi的信号:

3 指纹库扩充

3.1 指纹清晰度匹配聚类

定位测距中，常利用一致的路径损耗模型将接收信号功率与距离相关联，实现以信号强度估计目标距离。 但多信号源间的互耦干扰，使得同一AP在不同区域内或不同AP 在同一区域内的路径损耗程度，都不尽一致，并且全局的路径损耗指数也同时受到AP 所处高度的影响[12]。 由于这种波动性，复杂的室内环境下，来自多AP 的WIFI 信号，无法以固定或单一的路径损耗模型加以拟合；另一方面，人为地根据信号变化特征，简单地对目标区域进行划分以及选取最佳路径损耗指数并不具有理论的说服力。

因此，为了能够准确并且客观地拟合WIFI 信号在复杂室内环境下的分布情况，算法引入指纹清晰度概念，侧面地体现路径损耗指数的变化程度，并结合密度峰值聚类(Density Peek Clustering，DPC)[13]，实现对目标区域的自适应划分。

3.1.1 指纹清晰度

SRPr可根据与邻近SRPr1的信号差与距离差，确定SRPr处来自APi的指纹清晰度di r，如式(2)所示，间接体现样本区域内，不同SRPr位置的信号波动程度，以反映路径损耗指数的区域性变化。

式中:srssir1表示SRPr的邻近参考点编号组成的集合A中第r1 个编号所对应参考点的信号强度值，Num(·)表示·集合所包含的元素个数。 对A集合容量进行适应性调整，可改变SRPr对周围空间的清晰度感知范围。

通常而言，信号变化程度相近区域内的SRP，彼此间的信号差值与距离差值应互相逼近，使得参考点间的指纹清晰度也趋于一致。 因此，不失一般性的认为:具有相似指纹清晰度的参考点处的路径损耗指数，也具有较高的相似性。 故对于基于信号波动区分度及路径损耗指数特征的聚类，可以转化为基于指纹清晰度的聚类过程。

3.1.2 密度峰值聚类

改变传统指纹聚类中基于SRP 所有接收信号特征进行分区的思路，调整为仅针对某AP 发出信号在不同SRP 处指纹清晰度的相似度进行聚类分区。 由于室内建筑结构和材料的复杂性以及测量偶发误差的影响，势必会存在某SRP 的信号强度与周围信号强度值无明显相关性的极端情况，针对这种清晰度异常指纹点，为防止产生分区错误，参考点间的空间相关性也应作为聚类的指标之一。 因此，算法根据SRP 的指纹清晰度和平面坐标，对参考点进行三维泛化，以实现聚类分区。

对于待聚类的已采样参考点集合SRP，将每个SRPr处指纹清晰度dir及平面位置(xsra，xsrb)联合构建SRP 的映射三维空间。 则任意SRPr和SRPr1间的空间间隔fr，r1可以欧氏距离表示，如式(3)所示:

式中:为了保证dir与(xsra，xsrb)对聚类结果影响的一致性，将dir转化成以指纹清晰度极值差值约束下的单位数值，将(xsra，xsrb)转化成以平面位置极值差值约束下的单位数值，实现对不同尺度下聚类参数的一致化处理。

令SRPr处的近邻局部密度为:

式中:截断距离fcut由空间内各SRP 的平均期望近邻SRP 数量占SRP 总数的比例计算得到。

令{q1，q2，…，qc，…qC}为各SRP 近邻局部密度ρr的降序序列编号，其中C＝R，则SRPr处的父级距离可表示为:

式中:ID(·)表示满足表达式·的变量编号。 至此，每个SRPr都有用以综合描述路径损耗特征相似性及空间聚集程度的一对(ρr，θr)。

3.1.3 SRP 聚类

在三维空间下，SRPr处的局部密度ρr与其周围拥有相似信号波动程度的SRP 数量呈正相关，因此拥有更多相似SRP 的高ρr取值SRPr，其指纹清晰度更能体现所处区域内大多数SRP 处的信号变化特征。 同时，θr描述了SRPr与其最近距离的高局部密度SRP 的空间间隔。 因此，为满足聚类中心处SRP 聚集、聚类中心间分散分布的特性，应选用局部密度ρr较大，父级距离θr较大的SRP 作为聚类中心。

由于大多数室内场景中AP 设备的异构性，来自不同AP 的信号波动程度不一。 为了使不同分区的路径损耗指数尽可能地体现所在分区内的信号变化特性，分区数目应能自适应地跟随环境信号变化。 论文通过确保粗粒度筛选的SRP 聚类中心在具有高局部密度和长父级距离的特征的同时，各分区间的类间距离Γr，r1也应不低于高区分度的阈值ν，以此滤除高耦合类的聚类中心。 基于上述过程，目标区域内，对接收APi信号的SRP 的聚类流程如表1 所示。

表1 已采样参考点聚类流程

表1 中，step1 ～step4 实现了对聚类中心的初步筛选表示所有SRP 局部密度的上四分之一位数，表示所有SRP 父级距离的上四分之一位数；step5 ～step14 实现了非聚类中心SRP 的归类，Classify(·)表示参考点·所归类聚类中心的编号，论文采用逐层扩充的方式实现非中心点归类；step15 ～step23 实现了高耦合类的剔除，类间距离Γr，r1采用常见均值类距计算方式，ν为类间距离阈值。Ωi为接收来自APi信号的SRP 的最终分区结果，具体可表示为Ωi＝{｜1≤k≤Num(Ωi)}，Oik为Ωi包含的子区域。

3.2 信号预测

传统路径损耗模型通过AP 周围参考点的信号特征和AP 与待插值点间距离，直接对信号强度进行预测，而当信号传播路径中存在拐角、墙壁等障碍物时，信号波动加剧，拟合误差跳动明显。 为避免AP 与IRP 间未知因素对预测结果的干扰，算法通过将SRP 处的RSS 特征作为路径损耗模型的初始信号值，加强SRP 信号强度在模型预测中的影响，同时构建IRP 与SRP 信号强度与距离关系的差值表达式，取代传统路径损耗模型，间接消除障碍物影响。

图1 给出了传统路径损耗模型预测和近邻插值预测的对比，相比于图1(a)中选择APi单一邻近SRP 对处于不同位置的IRP 进行插值，图1(b)利用与IRP 处于同一分区内的SRP 对IRP 处信号进行预测计算，保证IRP 与SRP 拥有类似信号强度波动特征的同时，有效避免信号传播过程中墙壁等因素对插值的干扰。

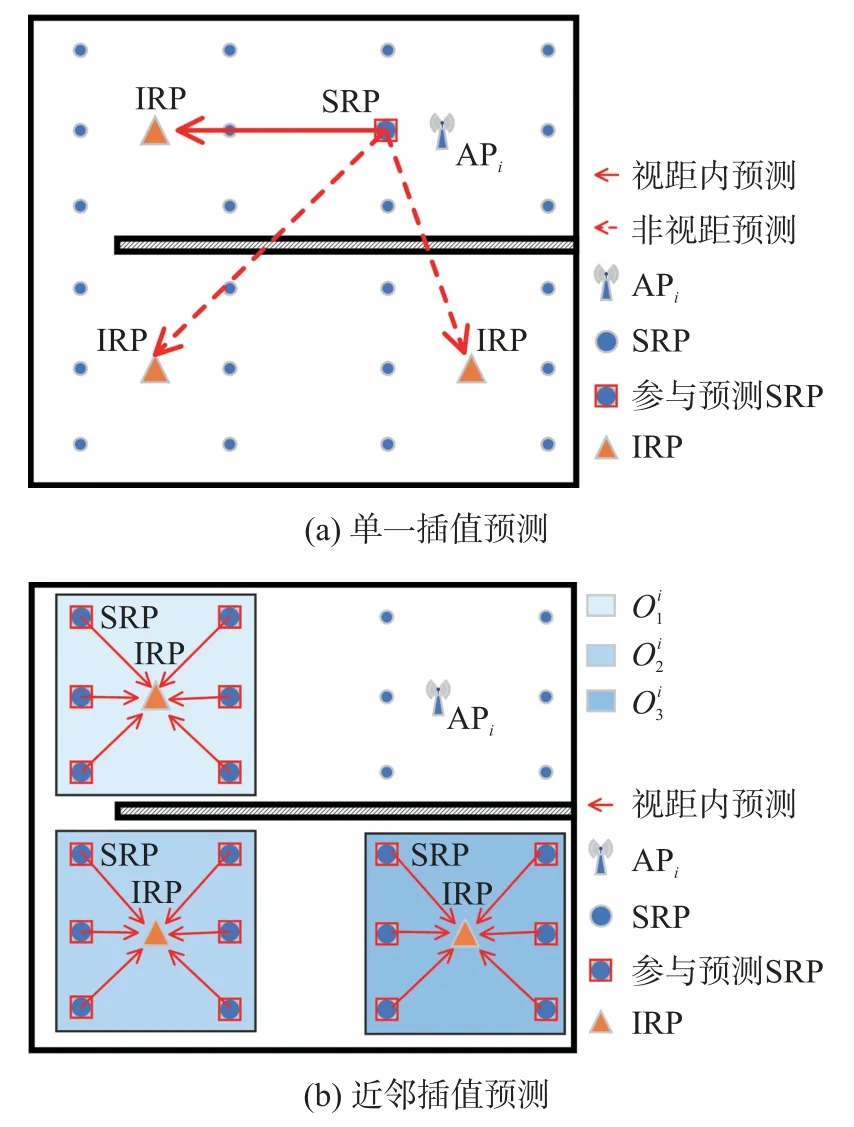
图1 单一模型和近邻模型的两种预测方法

3.2.1 差值近邻信号模型

若已采样参考点SRPr对来自APi的信号预测采用传统路径损耗模型:

式中:srssi0表示距离APi默认距离dis0处的信号强度损耗值，disr表示SRPr与APi的空间距离。

室内环境中，AP 与待插值点间的信号传播往往存在物理阻隔，导致直接以AP 处RSS 信号强度，在对数空间距离尺度上进行的插值预测会产生较大偏差。 由于室内定位关注的是信号强度相对量，因此可以将传统路径损耗模型构建成待插值点IRPz与已采样参考点SRPr信号强度的差值表达，即以SRPr处信号特征作为初始信号强度，仅需考虑SRPr与IRPz间的信号传播损耗。 此时，IRPz处的预测信号强度更多地取决于邻近SRP 处的信号特征。 则IRPz相对于SRPr的差值近邻信号模型表达式如下:

3.2.2 预测插值

为确保IRPz与参与其插值计算的邻近SRP 具有相似的信号波动特征，也应对IRPz进行分区归类。 由于对于IRPz的信号预测多取决于其邻近SRP，因此对IRPz的分区遵循类似无监督K近邻归类算法的“从众”原则。 即考察距离IRPz最近的K个SRP 的分类情况，将IRPz归类至拥有最高SRP数量占比的分区Oik内。

以单一SRP 进行预测可能产生由信号漂移导致的插值误差，以Oik内所有SRP 对IRPz插值结果均值的方式对上述漂移进行平滑处理。 令U＝{urk｜1≤rk≤Rk}为分区Oik内所包含Rk个SRP 的编号序列，结合分区内SRP 所观测到的来自APi的信号强度和SRP 的差值近邻信号模型，对IRPz的信号强度irssiz进行预测:

式中:ηuj为已采样参考点SRPuj对应的路径损耗指数，可由同一Oik分区内已知SRP 的信号强度与AP间距离拟合得出[14]。

4 参考点清晰度匹配优选

传统定位通过对离线指纹库和在线RSS 进行欧氏距离匹配，但由于信号波动以及测量误差等不确定因素，会出现空间距离较远但欧氏距离较近的异向RSS 向量对，导致定位精度下降。 同时在插值指纹库与真实指纹库间存在的信号强度差，会提高异向向量对的出现概率。

鉴于指纹清晰度不仅可以描述RP 处RSS 信号对于位置的辨析能力，也可以作为不同分区内RP的区分指标之一。 因此，提出基于指纹清晰度匹配的参考点筛选定位算法，通过匹配指纹清晰度，剔除异常参考点，留存高辨析RP 子集，提升插值指纹库的辨析力。

4.1 RP 筛选

由于指纹清晰度的计算需综合考量RP 本身及其邻近RP 的信息，即具备区域相关性。 当待定位RSS 向量L与指纹库中某RP 处存储的RSS 向量为异向向量对时，以L作为该RP 点处RSS 计算出的指纹清晰度，会明显区别于原始RSS 计算出的指纹清晰度，即向量L在RSS 上贴近RP，而在指纹清晰度上远离该RP。 根据这种区域相关性，剔除向量L异向RP，并进行参考点集的筛选修正，具体步骤如下:

步骤1 将待定位点向量L代入离线插值指纹库中每个RP 的位置，计算L在RPj处来自于APi的指纹清晰度diL，并与RPj的原指纹清晰度dij比较，令γ为清晰度差值阈值，若满足｜｜＜γ，则将RPj加入L的关于APi的RP 匹配集合SiL。

步骤2 按照RPj所处分区内所有SRP 的平均清晰度对SiL集合内的预选参考点进行降序排序。依据平均清晰度以及清晰度差值对预选参考点赋予相应的权重wij:

式中:为RPj所处分区的平均清晰度，σ为清晰度差值放大系数，放大系数的选取取决于RP 的放置粒度与信号波动程度，根据实际环境情况进行设定。

步骤3 令R＝{rs｜1≤s≤S}表示步骤1 中RPj可入选的SiL所对应AP 的编号集合。 则每个参考点RPj的总清晰度权重wdj可表示为:

根据所得清晰度权重wdj，取前B个权重最高的RP 作为支撑待定位向量L最终RP 集合SL。

4.2 位置计算

最终参与目标位置计算的RP 应满足在指纹清晰度与欧氏距离双尺度上逼近待定位向量L。 因此，综合SL内RP 的清晰度权重wdj和RSS 向量欧氏距离权重woj，得到RPj的组合权重，选取前E个组合权重最高的RP 参与目标位置计算。 则对待定位向量L的位置XL进行预估的表达式如下:

5 算法流程

论文提出的DIFS 扩库定位算法的步骤流程如图2 所示。 离线阶段，通过计算各个SRP 的指纹清晰度来体现路径损耗指数的分布特性，结合密度峰值聚类算法，对目标区域进行分区。 构建差值表达式，加强SRP 信号值对IRP 插值结果的影响，并拟合路径损耗指数。 结合SRP 分区结果，实现待插值点归类的IRP处信号近邻插值。 在线阶段以指纹清晰度的区域相关性，对填充后的RP 进行加权筛选，结合欧氏距离权重以及清晰度权重计算参考点参与定位运算的组合权重，预估待定位向量的空间坐标。

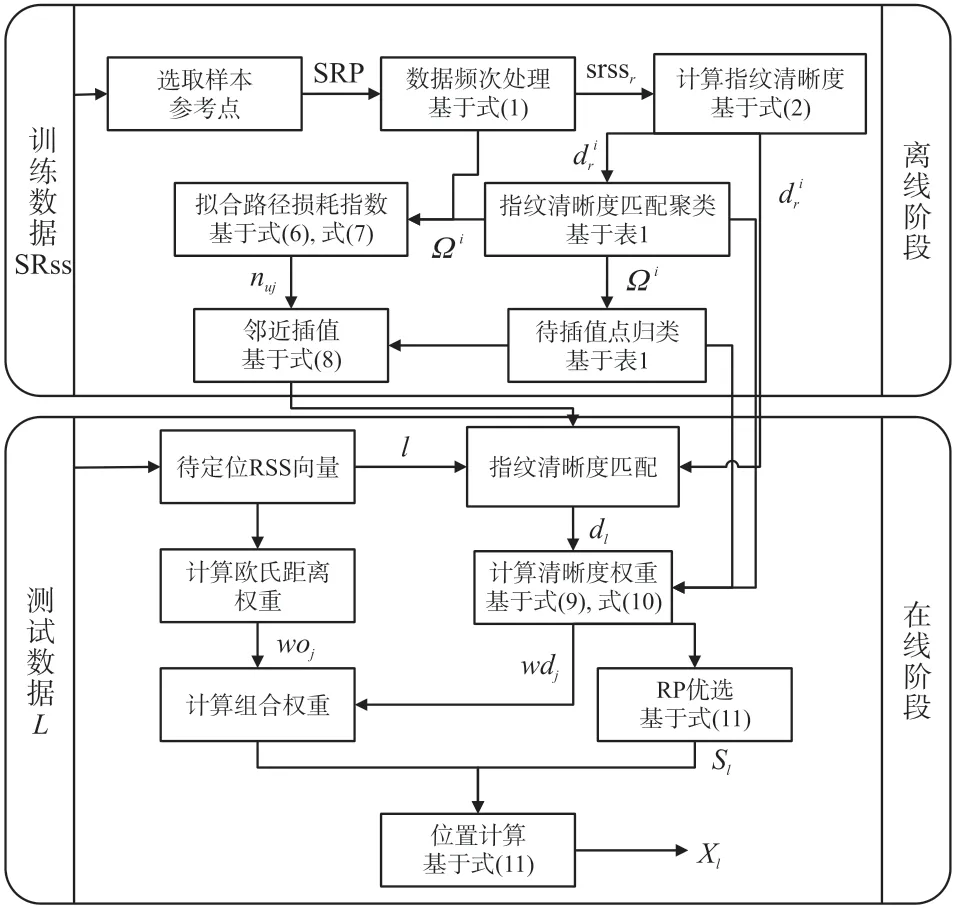
图2 DIFS 算法流程图

6 实验结果与分析

6.1 测试场景与数据处理

为了评估DIFS 算法的性能，以江南大学物联网工程学院某完整楼层进行数据实测RSS 的验证。该室内环境为60 m×42 m 的环形走廊。 沿走廊均匀设置M＝370 个RP，按比例pt 在370 个RP 中抽取370×pt 个SRP，其余RP 作为IRP 的验证集合。离线阶段在每个RP 处采集30 次指纹数据，采样间隔为2.3 s。 在环形走廊的4 个拐角及南北走廊的中间处布置N＝6 个品牌与型号均各异的AP 以体现AP 设备的差异性与波动。 每个RP 处未探测到的AP 信号强度值用-100 dBm 表示。 在线阶段，测试人员手持智能设备沿着走廊行走一周，得到一个矩形测试轨迹，并记录该轨迹上187 个测试点的位置及对应的RSS。 论文选取截断距离比例为0.01，类间距离阈值v＝0.05max(Γr，r1)，清晰度差值放大系数σ＝2。

6.2 分区性能分析

为验证指纹清晰度对信号强度波动的还原能力，场景内采取邻近RP 邻近编号的原则，测量并统计给定AP1下，所有370 个RP 的信号强度及其指纹清晰度的变化情况，如图3 所示。 图3(a)中平缓区间内RP 的RSS 在低强度区间内波动，彼此间RSS 跨度小，路径损耗指数低，在实际定位过程中难以区分；跳变区间内RP 的RSS 在中高强度区间内波动，变化显著，在定位区域内匹配跳变区间内的RP 更容易实现对目标的精确定位。 对应于模糊性高，定位精度差的RP，指纹清晰度图中平缓区间内RP 的指纹清晰度也较低，而跳变区间内RP 的指纹清晰度普遍较高，反映了该区间内RP 具有高RSS跨度、高定位辨析能力的特性。

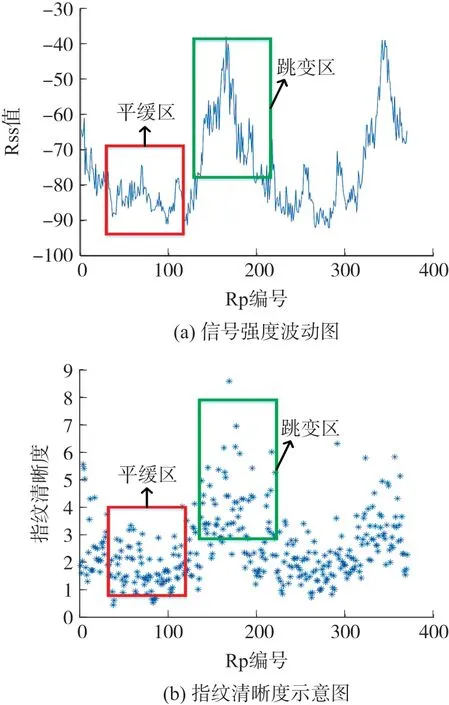
图3 信号强度波动与指纹清晰度对应图

同时，为验证聚类算法的有效性，按照pt ＝0.167的采样比例从离线参考点中均匀抽取370×0.167 ＝62 个RP 数据，组成初始指纹库SRP。 分别基于6 个各异的AP，对SRP 生成{Ω1，Ω2，…，Ω6}。由于AP 自身的设备性能不同以及所处的位置各异，每个AP 对于RP 的聚类分区情况差异较大。 随机选取的AP2和AP3的SRP 分区情况，如图4 所示。 AP2为外接移动电源的裸露WIFI 接入点，AP3为日常使用的家用路由器。 客观上，AP2的设备稳定性低于AP3。 因此在图4(a)中，接收来自AP2信号的SRP 被聚类成了5 个区域，说明AP2的信号波动在本环形走廊环境下更多样化。 与之相比，图4(b)中AP3的分区数目较AP2减少了2 个。 从实验环境本身来看，图4 中聚类区域的变化多发生在走廊转弯处或存在明显阻隔的地方，消防门的存在导致图4(a)与图4(b)均在平缓处产生了子区交界。 由此可见，论文所提的聚类方法能较好地反映目标区域内路径损耗指数的变化分布情况。

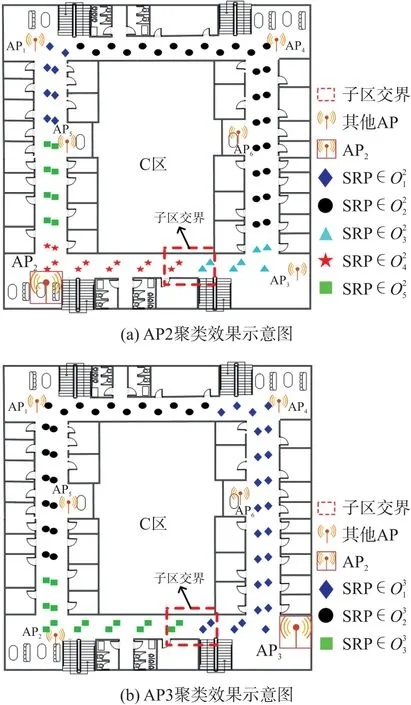
图4 AP2 和AP3 聚类效果示意图

6.3 预测性能分析

为验证SRP 数量对插值精度的影响，分别按照pt＝0.1，pt ＝0.167，pt ＝0.5 的比例从离线阶段所采集的参考点中均匀抽取参考点作为SRP，剩余参考点作为IRP，并通过比较离线阶段IRP 处的实际信号强度与算法预测值来验证插值效果。

表2 给出了在不同插值比例下，论文插值算法在各个AP 点的平均拟合残差。 可以看出，当pt ＝0.167 时，各AP 的插值综合效果最好，当pt ＝0.1时，低密度的SRP 包含的预测信息较少，导致预测精度较低。 而当pt＝0.5 时，高密度的样本参考点对于部分AP 的信号预测产生了有利影响，但信息的冗余还是导致了整体的插值效果下降。 可见，论文所提插值算法，不以贪婪式提升已采样数量，来获取高精度插值，降低了高精度插值场景的应用门槛，论文的后续测试中，均选取pt＝0.167。

表2 不同抽取比例下的插值平均误差 单位:dbm

进一步，对比测试了反距离加权插值、克里金插值、传统路径损耗模型预测3 种插值算法与论文插值算法在插值精度上的性能。 图5 给出了4 种插值算法在各AP 对于各IRP 处真实值与预测值的拟合残差箱型图。 可以看出，反距离加权算法由于只对RSS 信号的分布特性做简单的线性处理，在各个AP点的拟合误差较大，产生了最大的误差极值。 传统路径损耗模型没有考虑路径损耗指数在整个区域内的变化情况，导致其在复杂室内环境的预测效果不佳。 克里金插值算法在变异函数拟合时无法考虑不同AP 在具体室内环境下的信号传播特性的不同，在部分AP 处的预测精度明显低于论文算法，且存在较多的离群点，而论文所提插值算法的插值精度在误差极值、中位数以及误差离群点数量方面均优于其他三种插值算法。 在效果最好的AP2处，DIFS算法的平均拟合残差达到了2.79 dbm，较克里金算法、路径损耗模型、IDW 三种算法分别提升了18.3%、33.2%和64.2%，而在其他AP 处，论文算法也有显著的优势。

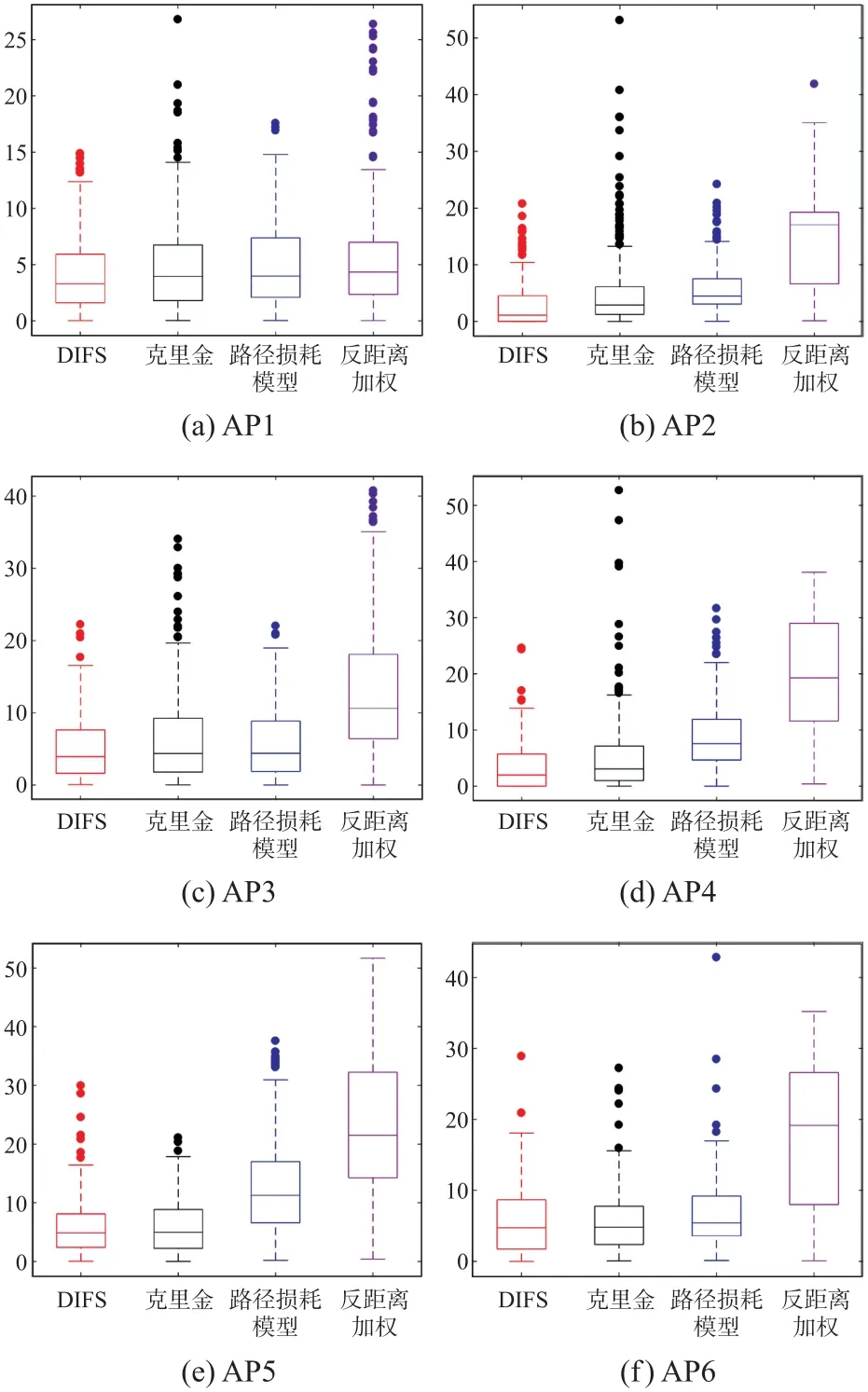
图5 4 种插值算法的拟合残差箱型示意图

6.4 参数影响分析

为分析筛选阈值γ和筛选个数B对于定位性能的影响，进行不同参数组合下的误差分析。 图6为两种参数的不同组合下测试向量的平均定位误差。 从图6 可以看出，筛选阈值γ 过大或者过小都会导致异向RP 进入筛选集合中，导致定位精度下降。 筛选集合RP 个数B过大同样会导致异向RP进入筛选集合，过小则可能导致优质RP 被忽略。同时，在分析过程中发现了参数的最佳工作状态，因此，参数配置为B＝28，γ＝0.16。

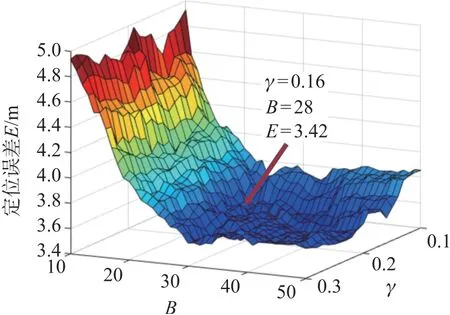
图6 不同参数组合下的平均定位误差

6.5 定位性能对比实验

由于指纹库扩充服务于定位，因此以定位性能来评测指纹库的插值价值。 为验证DIFS 算法整体的定位性能，分别将论文算法与克里金插值算法与LWKNN 定位算法、路径损耗模型插值算法与MCMC 算法以及原始指纹库与WKNN 算法等三种组合算法进行性能比较。 为保证实验对比的公平性，其他三种组合算法均选取当前指纹库的适配定位算法，且4 种定位算法均选取4 个最近邻参考点参与位置计算。

图7 给出了4 种扩库定位算法误差的累积概率分布。 可以看出，论文所提算法在估计误差达到3 m 之内的测试点数量达到了62%，而其他算法均不足60%。 表3 给出了四种扩库定位算法的位置估计误差值，DIFS 的平均定位误差和最大定位误差均小于其他三种扩库定位算法。 DIFS 算法在定位精度方面相较于其他三种扩库定位算法分别提升了16%、14%和19%。 在进行位置估计时，DIFS 算法拥有最高的定位精度，体现了DIFS 算法在复杂室内环境下，能减少人力成本，同时能维持良好定位精度。

图7 4 种扩库定位算法误差的累积概率分布

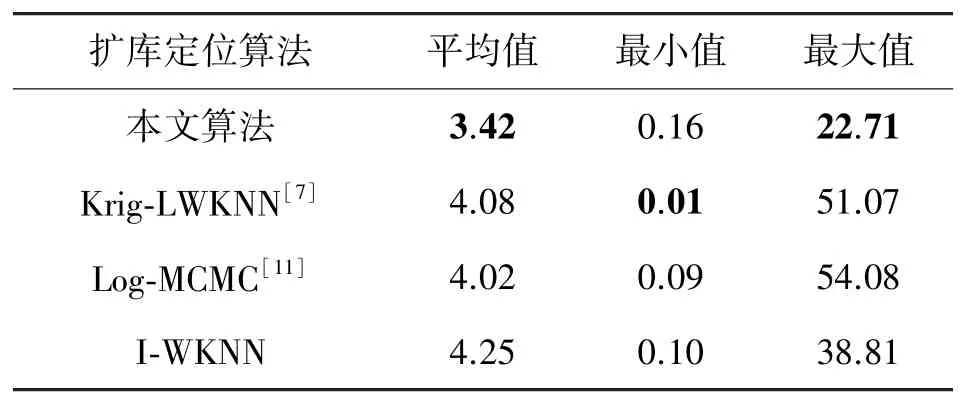
表3 4 种扩库定位算法位置估计误差 单位:m

7 结论

论文针对复杂室内环境下指纹库扩充信号预测失准，插值指纹库定位精度偏低的问题，提出了一种新的指纹库扩充与RP 优选定位算法。 通过引入指纹清晰度匹配，描述路径损耗指数的区域性特征，同时构建差值近邻传播模型以实现精确插值。 在线阶段结合欧氏距离权重和清晰度权重筛选优质参考点参与最终定位运算。 实验证明，所提DIFS 算法，实现了小样本下的高质量全局指纹库扩充，以双尺度权重匹配提高在线定位精度，相较于其他传统扩库定位算法具备更高效的室内定位性能。 同时，无线接入点的选择可作为进一步提高指纹库质量的切入点。