拱肋高度基于余弦曲线变化的钢管混凝土拱桥设计方法

周水兴,白兴蓉,王 鹏,邓业逵

(1.重庆交通大学 土木工程学院,重庆 400074;2.中交公路规划设计院有限公司贵州分公司,贵州 贵阳 550003;3.中建三局第三建设工程有限责任公司,湖北 武汉 430074)

0 引 言

国内高速公路、铁路和城市道路的建设推动了钢管混凝土拱桥的快速发展,使之成为跨越峡谷、江河的主要桥型之一。2020年建成的广西平南三桥计算跨径达560 m,700 m级钢管混凝土拱桥也已开展相关研究[1]。围绕钢管混凝土拱桥力学行为和施工技术,国内学者已开展了较为深入的研究[2-6],然而针对钢管混凝土拱桥拱肋截面高度设计的研究很少,仅张建民等[7]开展了南宁永和大桥两种设计方案的拱肋高度比选分析,未对变截面高度设计方法做深入研究。目前设计人员大多采用李特(Ritter)公式进行钢管拱的变截面设计[8]。李特公式是将拱顶与拱脚截面的拱厚系数分别取为1和n,将拱顶与所求截面的惯性矩之比以拱厚系数在1～n内按线性内插来计算截面高度。李特公式概念清晰,但需要事先拟定或计算拱厚系数,且按李特公式设计的钢管混凝土拱,其拱脚截面上、下弦管轴力差异较大。

为此,笔者分析了李特公式中影响截面高度的设计参数,将其归结为与拱轴水平倾角相关的单一参数,在此基础上提出了将截面高度定义为拱顶高度与其所在位置的拱轴水平倾角余弦值的幂次方之比的一种设计新方法,给出了幂次方的求解过程和取值范围。为验证文中方法的可行性,开展了两座钢管混凝土拱桥的实桥分析,对比了按文中公式、李特公式和设计文件所设计的拱肋高度及其对动力特性与弹性稳定的差异。文中方法可为今后钢管混凝土拱桥钢管拱设计提供参考。

1 李特公式

计算钢管混凝土拱桥拱肋变截面高度的李特公式如式(1)[8]:

(1)

式中:Id为拱顶截面惯性矩;I为距拱顶x处的截面惯性矩;n为拱厚系数;φ为距拱顶x处的拱轴水平倾角;ξ=2x/L,L为计算跨径。

四肢钢管拱截面如图1。图1中,Hd、Ha分别为拱顶、拱脚截面的中心高度。

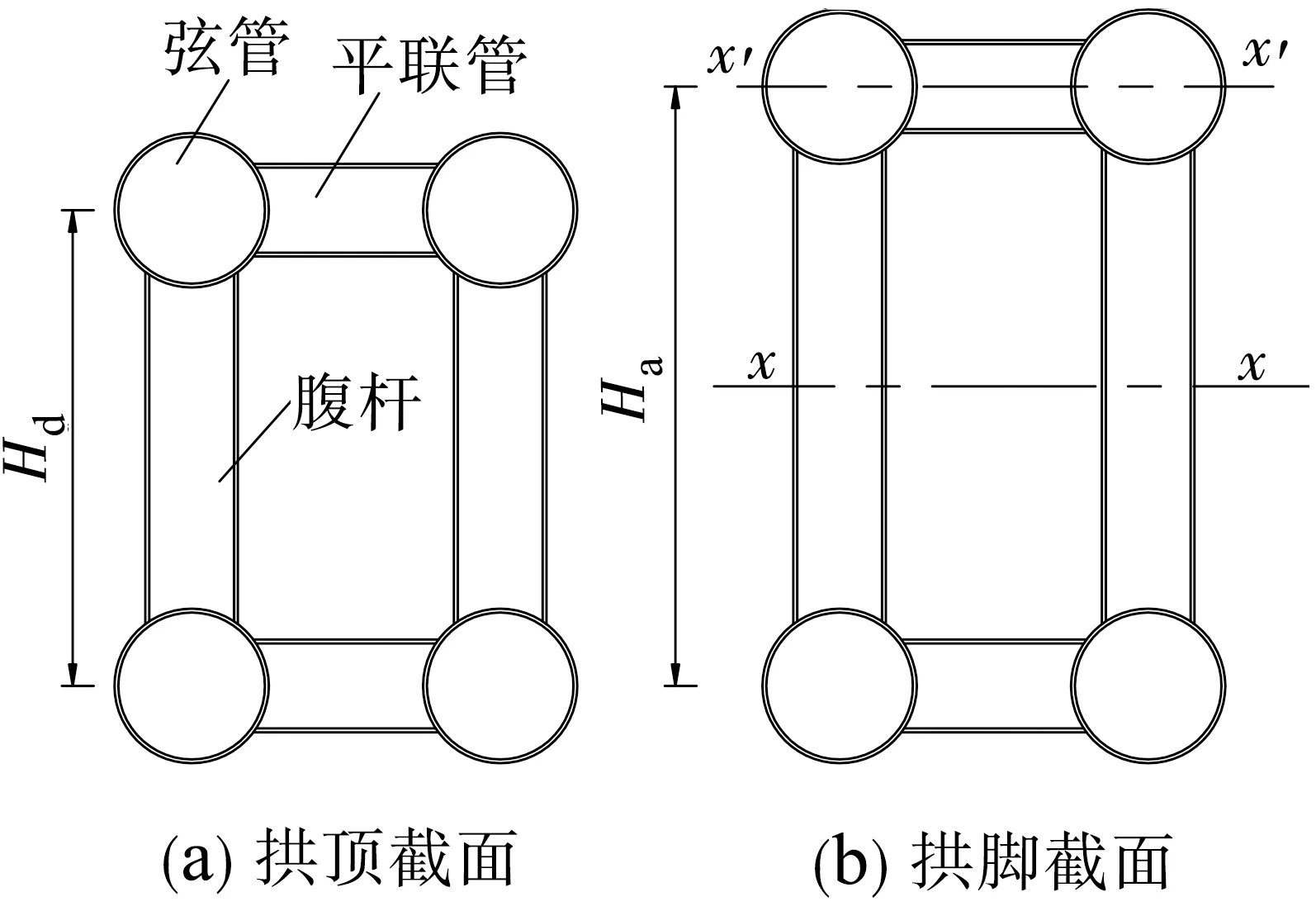
图1 四肢钢管拱截面

截面惯性矩计算公式如式(2)[8]:

(2)

式中:ID、As分别为上、下弦管对自身形心轴(x′-x′)的惯性矩和截面积。

弦管对自身形心轴的惯性矩ID如式(3):

(3)

大跨度钢管混凝土拱桥弦管直径D通常取1 000～1 500 mm,壁厚t取22～36 mm,t/D=0.022～0.024,则式(3)可近似为:

(4)

通过对已建大跨度变截面钢管混凝土拱桥的统计,拱顶和拱脚处的弦管直径与其截面中心高度之比分别在0.20～0.24和0.10～0.15之间,其平分值在0.01～0.06之间,将式(2)简化为:

(5)

经简化,式(5)与式(2)相比,误差在3%以内。

将式(2)代入式(1),得到任意截面高度H和拱厚系数n计算公式如式(6):

(6)

(7)

式中:φa为拱脚截面的拱轴水平倾角。

2 一种新的变截面高度设计公式

2.1 按拱轴水平倾角余弦值的幂次方计算

(8)

将式(8)代入式(6)中的分母项,并令:

(9)

式中:β=α+0.5。

由此,拱肋截面高度可按式(10)计算:

(10)

式(10)表明,拱肋截面高度仅与拱顶高度和拱轴水平倾角有关,无需李特公式中的拱厚系数。

2.2 幂次方β的确定

钢管混凝土拱桥设计中,需事先拟定跨径、矢高、拱脚截面高度、拱顶截面高度和拱轴线方程,代入式(10),得拱脚截面高度为:

(11)

将式(11)改写为:

(cosφa)β=Hd/Ha

(12)

以cosφa为底,对等式两边取对数,得到β的计算式为:

β=logcosφHd/Ha

(13)

式(13)表明,β与拱顶截面高度、拱脚截面高度及拱脚拱轴水平倾角φa有关。φa又与矢跨比和拱轴线方程有关。矢跨比越大,倾角φa也越大,相应的cosφa和β值越小;反之,矢跨比越小,拱圈越平坦,cosφa和β值就越大。

当拱肋为等高度时,即Hd/Ha=1,代入式(10)有β=0和H=Hd,即所有截面高度都相等。

对于拱桥中常用的矢跨比和拱轴系数,cosφ值介于0.6～1.0之间。当β<1时,有cosφ<(cosφ)β,且β值越小,(cosφ)β值越趋近于1。从式(10)看出,拱圈截面高度沿跨径方向的变化趋小,因此适用于对截面高度变化要求不大的中小跨径拱桥中[8]。对于大跨度钢管混凝土拱桥,为使拱圈内力分布均匀,β应大于1,使(cosφ)β变小,以满足大跨度拱桥对拱圈截面高度变化的要求。

钢管混凝土拱桥中,一般取Ha/Hd=1.6～2.0,矢跨比取1/7～1/4,取拱轴系数m=1.3～2.0[9]。根据式(13),β=1.128～3.841。

3 实桥分析

为进一步验证文中公式在工程应用中的可行性,选取两座实际钢管混凝土拱桥开展钢管混凝土拱肋截面高度、弦管内力、动力特性、弹性稳定的对比分析。由于拱肋高度变化会影响到腹杆倾角,造成截面应力增大,因此需计算腹杆应力[7]。

3.1 实桥概况

3.1.1 四川犍为岷江大桥

该桥是一座净跨径400 m的中承式钢管混凝土拱桥,矢跨比f/L=1/4,拱轴系数m=1.45,拱轴线为悬链线。钢管混凝土拱肋采用四肢桁架结构,拱肋宽4.0 m,拱脚与拱顶截面中心高度分别为11.68、5.68 m。拱肋弦管为Φ1 320 mm×22(26、30、36)mm,管内灌注C60自密实混凝土。

3.1.2 贵州乌梅河大桥

该桥是一座计算跨径300 m的上承式钢管混凝土拱桥,矢跨比f/L=1/5,拱轴系数m=1.55。拱肋采用3榀空间桁架结构,每榀拱肋横向间距5 m。拱肋采用等宽变高截面,拱脚与拱顶截面中心高度分别为9.0、5.0 m。弦管为Φ1 200 mm×24(35)mm,管内灌注C55自密实混凝土。

3.2 拱肋截面高度比较

根据3.1节设计参数,犍为岷江大桥的Hd/Ha=5.68/11.68,cosφa=0.802 275,得β=2.099 5,拱厚系数n=0.340 24。分别按设计文件、李特公式和文中公式计算半跨拱肋截面高度,岷江大桥拱肋高度曲线如图2。从图2中可知,ξ在0～0.4(拱顶至L/5)区段内,按李特公式得到的拱肋高度要大于设计高度;从L/5至拱脚区段内,按李特公式得到的拱肋高度要小于设计高度,而按文中公式设计的拱肋高度均小于其他两种方法的高度,因此还可节省一定数量的钢材。

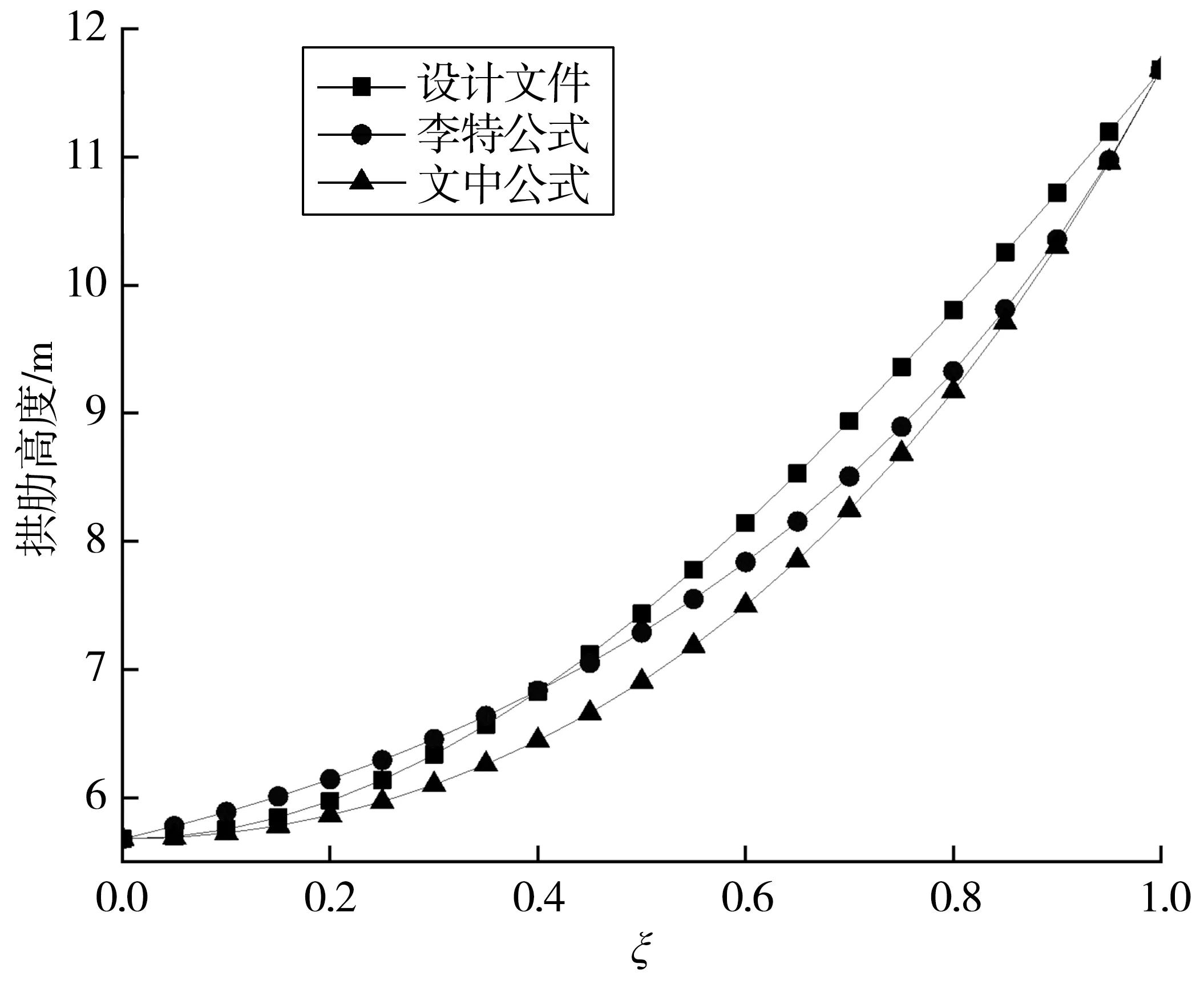
图2 3种设计方法得到的岷江大桥拱肋高度

建立有限元模型,考虑管内混凝土灌注过程,得到3种设计在成桥状态时弦管轴力(图3)。结果表明:3种设计方法得到的上、下弦管轴力接近,这与文献[7]的结论一致,即在保持其他设计参数不变的情况下,仅改变拱肋高度对弦管内力的影响很小;但在拱脚截面,按文中方法得出的弦管轴力与其他两种方法有所不同,与设计图相比,上弦轴力增大5.84%,下弦减小2.77%;与李特公式相比,上弦轴力增大1.70%,下弦减小0.88%,虽然轴力的变化量不大,但对以承受负弯矩的拱脚截面而言仍是有益的。造成拱脚截面上、下弦管内力变化的原因在于,采用文中方法设计的钢管混凝土拱肋,由于沿桥跨方向的截面高度变小,相应减小了拱脚截面的负弯矩。

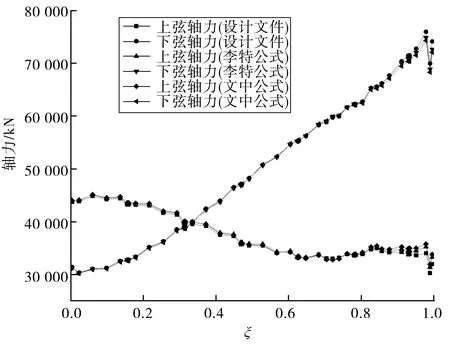
图3 岷江大桥拱肋上、下弦管轴力

乌梅河大桥的Hd/Ha=5/9,cosφa=0.755 907,β=2.100 5,n=0.408 31。分别按设计文件、李特公式和文中公式计算拱肋高度,结果表明,与设计文件和李特公式相比,以文中公式得到的拱肋高度最小,最大相差0.47、0.37 m,约为拱顶中心高度的0.094、0.074倍。半跨钢管拱上、下弦管轴力分布如图4。由图4可知,与设计文件结果相比,拱脚截面上弦管轴力增大1.97%,下弦管轴力减小0.97%;与李特公式结果相比,拱脚截面上弦轴力增大7.0%,下弦轴力减小1.71%。由此可见,按文中方法设计的拱肋,在一定程度上改善了拱脚截面的轴力分布。

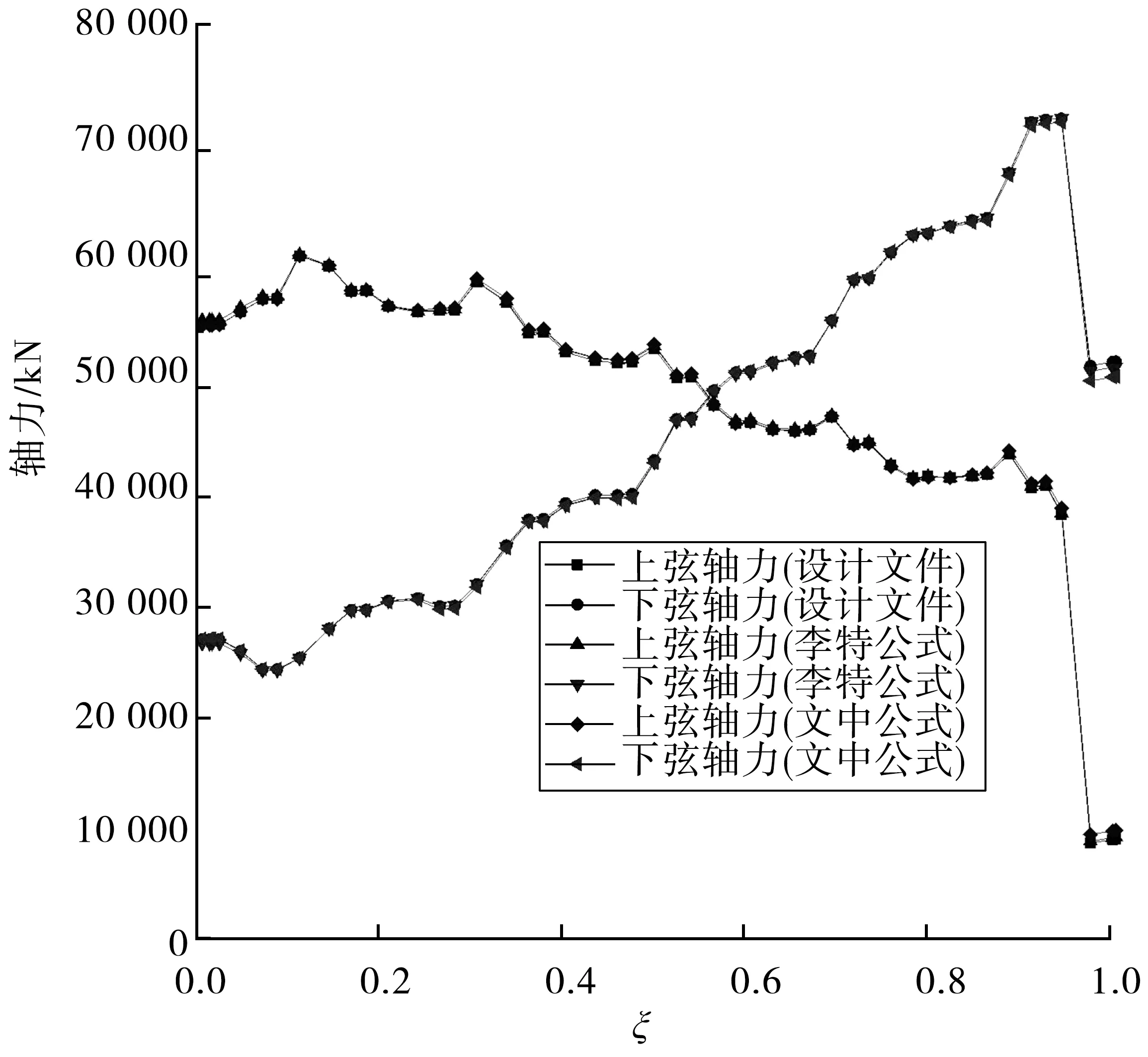
图4 乌梅河大桥拱肋上、下弦管轴力

3.3 腹杆应力比较

在保持腹杆间距不变的情况下,截面高度降低使腹杆倾角相应减小、腹杆应力增大,因此JTG/T D65-06—2015《公路钢管混凝土拱桥设计规范》[10]规定了腹杆夹角最小值的要求。表1列出了成桥状态两座大桥钢管拱腹杆最大拉应力和最大压应力结果对比,差异微小,原因是3种设计方法对应的钢管拱高度不大,没有显著改变斜腹杆的倾角。

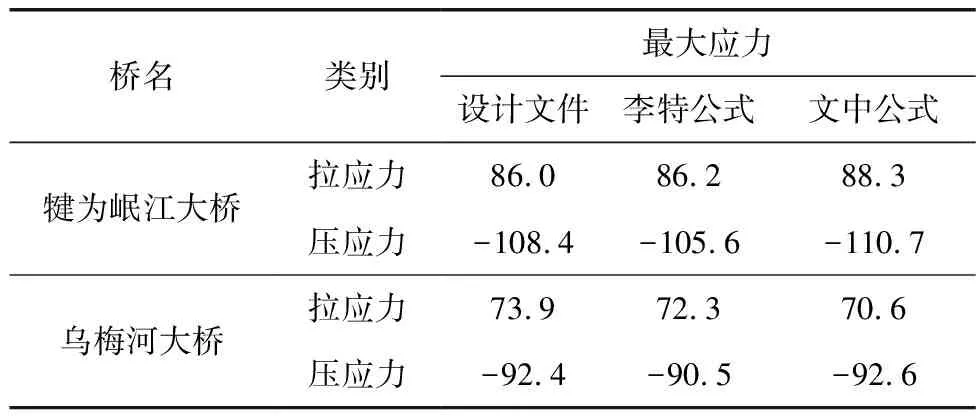
表1 腹杆最大应力

3.4 动力特性与弹性稳定系数比较

两座大桥在3种不同设计方法下前五阶的振型与频率如表2和表3。由表2和表3可知,频率值相差微小,振型也未发生改变。

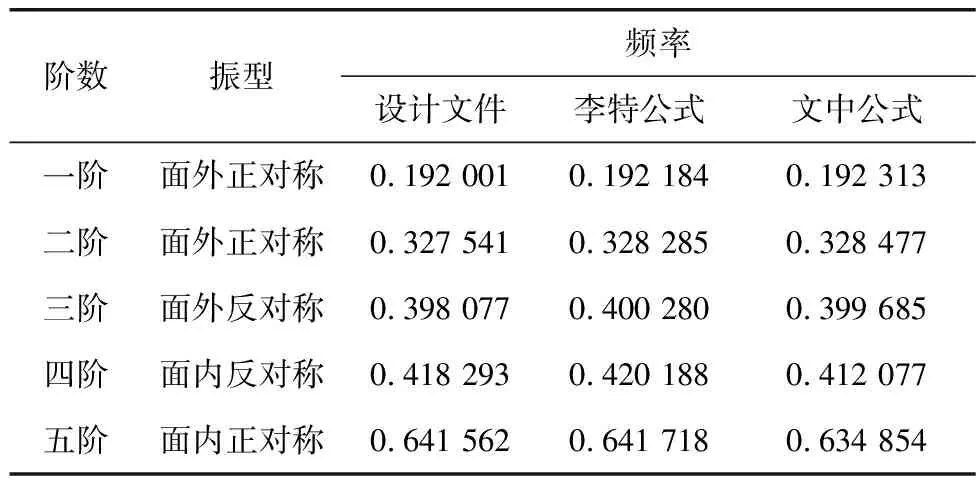
表2 犍为岷江大桥动力特性

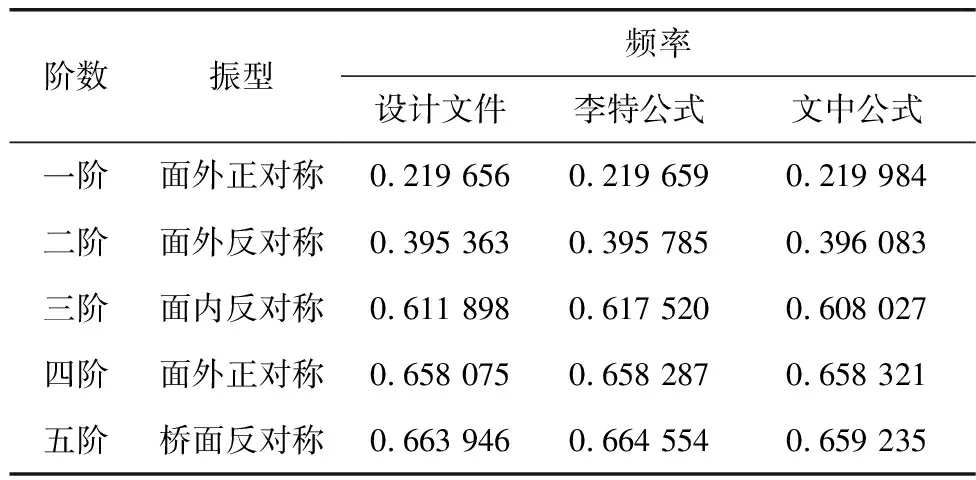
表3 乌梅河大桥动力特性

表4给出了3种设计方法所对应的一阶面外/面内失稳时的弹性稳定系数。其中:一阶面外稳定系数均以文中方法得到的结果最大,而一阶面内稳定系数以文中方法最小,是由于钢管拱高度减小降低了面内刚度,造成稳定系数的降低。但从数值看差异微小,文中方法仅比设计文件降低了4.71%和2.73%。

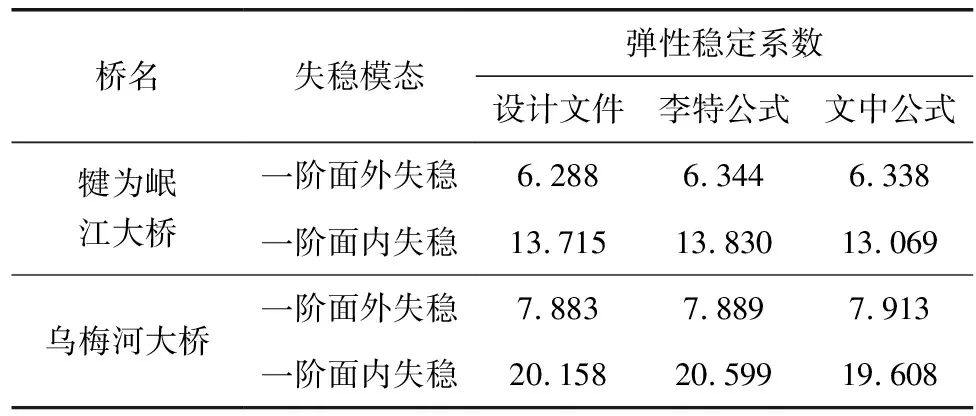
表4 弹性稳定系数

4 结 论

笔者分析了李特公式中影响截面高度变化的设计参数,在此基础上提出一种钢管混凝土拱桥变截面高度设计的新方法,通过两座实桥的动力特性与弹性稳定分析,得到以下结论:

1)笔者提出的钢管混凝土拱桥拱肋变截面高度计算公式H=Hd/(cosφ)β能够用于钢管混凝土拱桥的变截面设计。

2)在设计参数相同的情况下,用设计文件、李特公式和文中公式得到的弦管内力、腹杆应力、动力特性和弹性稳定差异不大,均能满足设计要求。

3)笔者提出的计算公式是针对钢管混凝土桁架拱桥变截面拱肋推导的,能否用于实腹式拱桥变截面设计,还需要做进一步研究。