高速公路避险车道制动坡床长度可靠性设计

张 航,刘 洋,吕能超

(1.武汉理工大学 交通与物流工程学院,湖北 武汉 430063;2.武汉理工大学 智能交通系统研究中心,湖北 武汉 430063)

0 引 言

受地形条件限制,山区高速公路存在很多连续下坡路段,一直以来该路段事故率较高,提高该路段的行车安全性成为交通安全保障的重点。根据多年的数据表明,在山区高速公路上设置避险车道对降低其交通事故的频率以及严重程度有良好的效果,尤其是避险车道中的制动坡床对于保障制动失效车辆的安全停车起着重要作用。

ITASCA[1]咨询集团已开发出PFC系列颗粒流分析程序软件,其中的PFC2D和PFC3D已经成为模拟固体颗粒力学问题的有效方法,用来代替作非常昂贵的实地足尺实验,如今许多对避险车道制动集料应用效果的研究常采用这种方法。F.A.CAPUANO等[2]制造了一种由胶结材料制成的预制可变形单元组成的替代材料,用于避险车道制动坡床,有一定的应用效果;马亮等[3]分析了可能影响避险车道填充集料阻力性能的因素,结合理论分析与实车运行试验数据建立了针对20～40 mm粒径砾石集料的阻力计算模型,可用于指导采用20～40 mm粒径砾石集料的避险车道的设计,并可参照此方法建立其它集料的制动性能计算模型;宋灿灿等[4-8]对避险车道的驶出角度、引道长度、左转和右转圆曲线处的流出角度等设计指标进行了详细研究,通过结合驾驶模拟,他们对这些设计指标进行了比较详尽的分析,并提出了相应的建议范围。以上均采用确定性方法对避险车道进行研究,不能对避险车道的安全可靠性进行定量评价。

鉴于此,越来越多的学者将可靠度理论引入道路设计领域,F.P.D.NAVIN[9]最先在道路设计中运用可靠度理论;张航等[10]考虑汽车的制动过程,结合可靠度理论对高速公路停车视距进行设计;唐宗鑫等[11]实测货车的速度和加速度,建立高速公路加速车道长度计算模型,利用可靠度方法,计算出加速车道的长度;王路等[12]基于可靠度理论,对临界坡长进行了可靠性分析并得到对应推荐值。总体来看,目前将避险车道与可靠度理论相联系的研究较少,笔者旨在将避险车道制动坡床的相关影响因素与可靠度理论结合起来,进行可靠性分析,并对制动坡床的安全程度进行量化评估。这将有助于推动可靠度理论在道路工程领域的应用,提高道路的整体安全性水平。

1 避险车道制动坡床

制动坡床是制动失效车辆受到其内填充材料作用而被强制减速停车的场所和避险车道的主要结构,如图1。其形式分为上坡道式、平坡道式和下坡道式,其中,上坡式是制动效果最好、运用最广泛的制动坡床设置形式,后两者为地形或成本受限时采用的制动形式,实际应用较少。因此研究对象为上坡道式制动坡床,针对其长度进行研究。

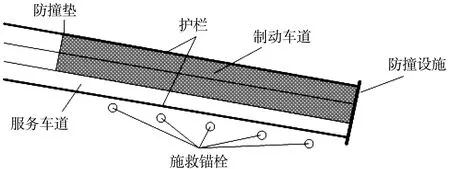
图1 制动坡床结构示意

合理的制动坡床能有效地使制动失效车辆安全减速停车,若制动坡床长度过小或填充材料不合理,可能导致制动失效车辆无法完全停止,可能发生冲撞制动坡床末端防撞设施甚至冲出避险车道外等次生事故。理论上制动坡床长度越长越能保证失控车辆的安全,但在实际应用中,制动坡床长度受到地形环境、造价成本、施工难度等因素的影响较大,应结合实际情况进行确定。

2 制动坡床长度可靠性分析

2.1 制动坡床长度可靠度功能函数

可靠度是指在规定的使用条件下,经过设计、制造、安装和维护后,结构能够在预定寿命内保持正常的功能、性能和安全的概率。当结构完成预期功能,即认为结构处于可靠状态对应的概率为可靠概率Ps,反之认为结构处于失效状态,对应的为失效概率Pf,Ps+Pf=1。在避险车道设计中应用可靠度理论将避险车道制动坡床长度小于安全值与失效状态相对应,并计算出失效概率以表示制动坡床可能存在的安全隐患。

制动失效车辆进入避险车道后,能使其安全减速停止而不会冲出制动坡床外的长度,记为LZR;将道路设计中提供的制动坡床长度,记为LZS。当设计制动坡床长度小于安全制动坡床长度时,认为道路设计失效,避险车道制动坡床设计存在安全隐患。

Z=LZS-LZR

(1)

2.2 制动坡床长度计算模型

制动坡床上车辆减速停车,是轮胎与坡床材料间滚动阻力和车重分力共同承担的结果,由能量守恒原理可得:

(2)

将速度单位转化为km/h并简化后得:

(3)

式中:v为失控车辆在避险车道入口的驶入速度,km/h;f为制动坡床填充材料的滚动阻力系数;i为制动坡床坡度;LZmin为避险车道制动坡床最小安全长度,m;LZ为避险车道制动坡度长度,m。

式(3)为规范中确定制动坡床长度的方法,由此可知v、f和i均对LZ有影响。规范认为高速公路避险车道制动坡床入口处的设计驶入速度建议值为100～120 km/h之间。

对于上坡型制动坡床,增大坡度会减少其长度,但从车辆纵向稳定性考虑,合理的制动坡床坡度应保证不发生纵向倾覆或倒溜现象。

2.2.1 纵向倾覆条件

如图2,上坡时当汽车前轮的法向支持力N1为0时,此时车辆可能绕后轮与坡面的接触点O2发生纵向倾覆。对O2点取矩可得:

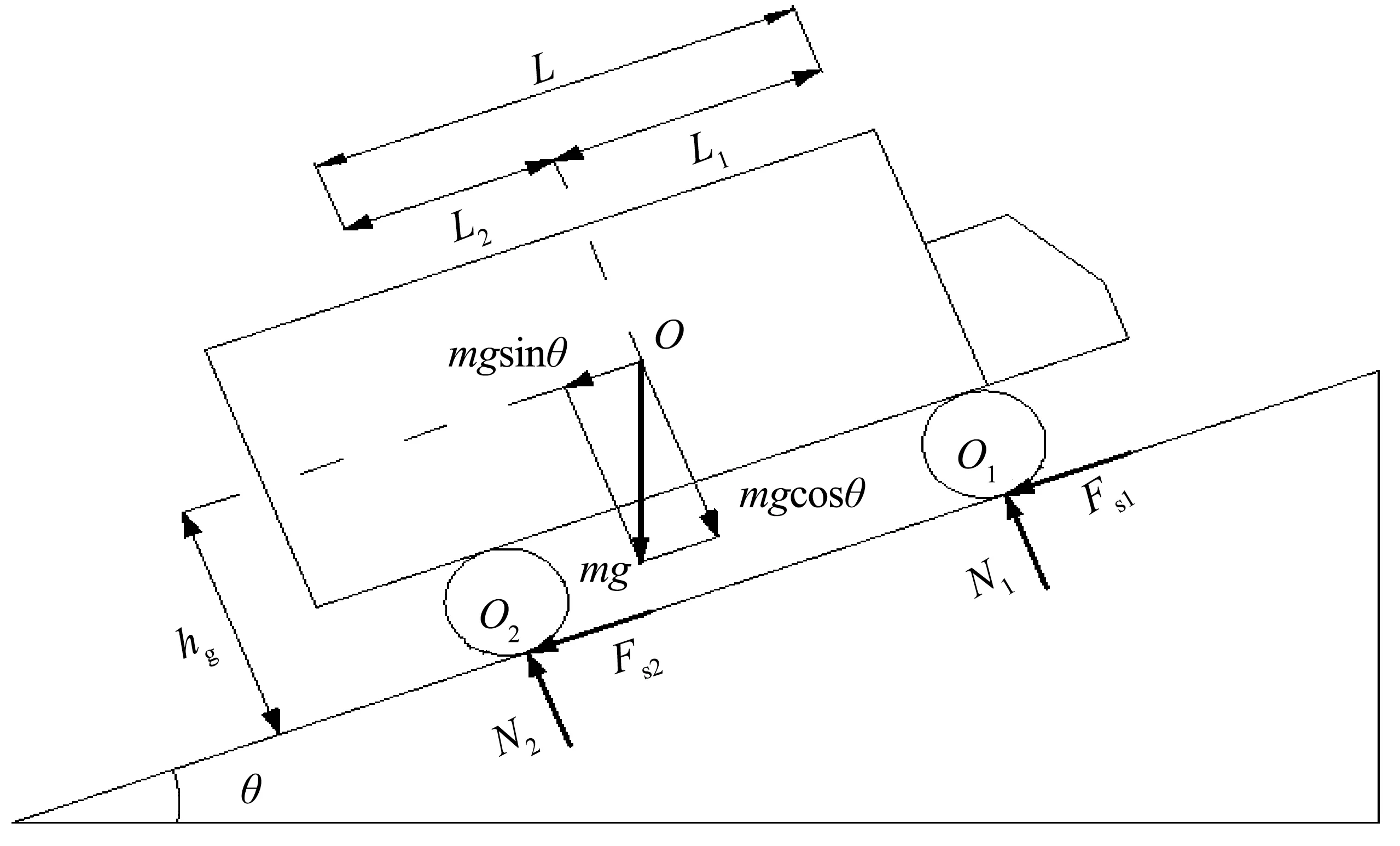
图2 汽车纵向稳定性分析

mgL2cosθ0-mghgsinθ0=0

(4)

(5)

式中:θ0为纵向倾覆极限纵坡倾角,(°);L2为汽车后轮与汽车重心水平沿坡面距离,m;hg为汽车重心离坡面高度,m;i0为纵向倾覆极限纵坡坡度,(°)。

当纵坡倾角θ>θ0时,即纵坡坡度i>i0,车辆发生纵向倾覆。

2.2.2 倒溜条件

当坡面材料对车轮的摩擦力小于重力沿坡面的分力时,车辆发生倒溜,根据极限平衡状态对车辆整体受力分析可得:

mgsinθ1=Fs1+Fs2=fmgcosθ1

(6)

i1=tanθ1=f

(7)

式中:θ1为倒溜极限纵坡倾角,(°);Fs1、Fs2分别为汽车前轮、后轮与坡面摩擦力,N;i1为倒溜极限纵坡坡度。

当纵坡倾角θ>θ1时,即纵坡坡度i>i1,车辆发生倒溜。

2.2.3 纵向稳定性保证条件

2.3 可靠度功能函数参数分析

2.3.1 避险车道入口处车辆运行速度v

现有研究表明[14]高速公路断面的运行速度服从正态分布,为验证避险车道入口处车辆运行速度v是否也服从正态分布,笔者选择了湖北沪渝高速宜昌长阳段K1 240(100 km/h)、湖北宜巴高速上海方向路段K1 178(120 km/h)、湖北宜巴高速重庆方向路段K1 190(80 km/h)3种设计速度上的直线和大半径平曲线路段的避险车道作为统计对象,测量大型车驶入避险车道时的速度,对测得的数据进行单样本K-S检验并整理如表1。

以95%的置信度为判断依据,由表1中的精确显著性水平结果可以知道,120、100、80 km/h 3种主线设计速度对应的最小值达到了0.716,远大于显著性水平0.05,证明所观测样本中大型车驶入避险车道的车速v满足正态分布。

2.3.2 制动坡床填充材料滚动阻力系数f

规范中对不同制动坡床填充材料的滚动阻力系数f取值规定详见表2。

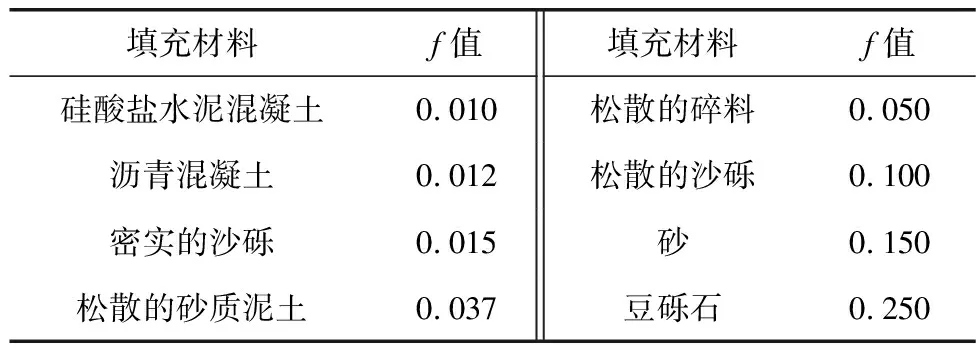
表2 制动坡床填充材料的滚动阻力系数

在实际应用中,制动坡床填充材料基本采用减速效果最好的豆砾石,少部分采用砂,因此材料滚动阻力系数f基本只取0.25或0.15,对LZ的影响分为两类讨论即可。

2.3.3 制动坡床坡度i

JTG TD81—2017《公路交通安全设施设计细则》要求制动坡床坡度i≤15%,由上文可知车辆纵向稳定性约束条件为i≤f,一般f只取0.25或0.15,因而制动坡床坡度i也应取15%以下的值,与规范要求一致。综合各影响因素进行选定,实际应用中一般有5%≤i≤15%,其分布频率不明。

3 制动坡床长度可靠性设计

3.1 可靠度功能函数求解

可靠度功能函数中的避险车道入口处车辆运行速度v入服从正态分布,而制动坡床填充材料的滚动阻力系数f和制动坡床坡度i的分布频率未知,三者为相互独立的随机变量。由于不能确定功能函数中所有的影响变量分布,故采用蒙特卡罗方法对f、i进行抽样模拟,结合已建立的制动坡床长度计算模型对可靠度功能函数进行求解。

为保证精度,笔者取抽样次数N=10 000进行抽样模拟。具体步骤如下:

1)确定抽样模拟次数N=10 000。

2)避险车道入口处车辆运行速度v由MATLAB软件根据表1已知的分布进行正态分布抽样模拟产生,制动坡床填充材料的滚动阻力系数f由MATLAB软件根据0.15(1-p=0.1)和0.25(p=0.9)的二项分布抽样模拟产生,制动坡床坡度i利用MATLAB软件从5%～15%之间随机抽样模拟产生,并带入功能函数式(1)中计算。

3)若某次抽样模拟后功能函数式中Z≥0,则定义此次抽样有效,同理Z<0时认为该次抽样无效。

4)统计可靠抽样的次数,除以总抽样模拟次数,计算可靠概率。

由于JTG TD81—2017《公路交通安全设施设计细则》给出的设计制动坡床长度LZS并非为定值,而是根据v、f与i的设计取值综合确定。其中,规范建议高速公路避险车道制动坡床的设计驶入速度最低取为100 km/h,与实际情况下制动失效车辆驶入避险车道的速度存在差异。

根据JTG TD81—2017《公路交通安全设施设计细则》给出的计算式(3)与v、f与i的设计取值,先确定设计制动坡床长度LZS,然后根据制动坡床长度可靠度功能函数式(1),通过蒙特卡罗法按上述步骤进行求解,得出的可靠概率Ps与失效概率Pf结果如表3。

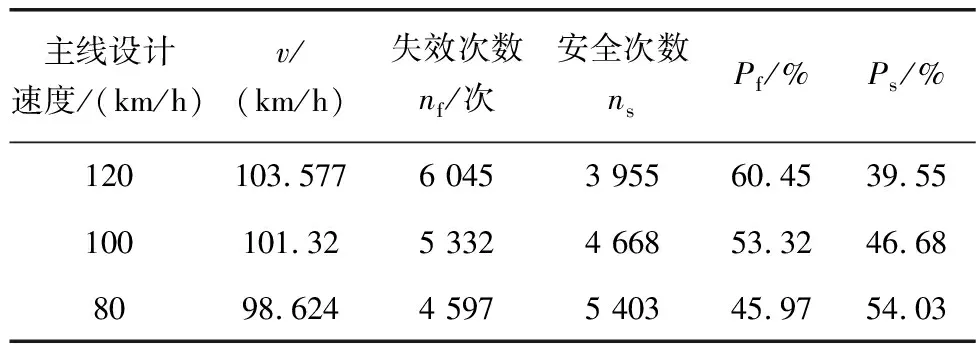
表3 制动坡床长度可靠度计算结果

3.2 计算结果分析

现有规范并未对避险车道制动坡床长度的可靠度作出明确规定。因此参考JTG D50—2017《公路沥青路面设计规范》和JTG 2120—2020《公路工程结构可靠度设计统一标准》中对高速公路路面结构目标可靠度的规定来确定高速公路避险车道制动坡床长度的可靠概率和失效概率,如表4,目标的失效概率为5%,对应的可靠概率为95%。

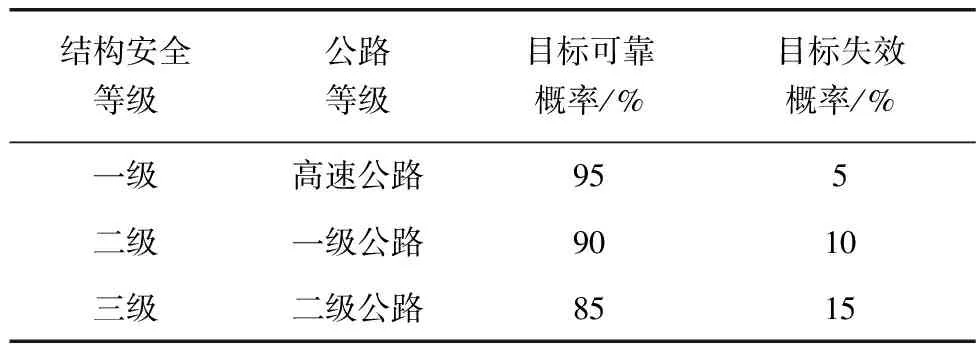
表4 不同安全等级对应的可靠指标与失效概率

由表3可得主线设计速度为120、100、80 km/h的避险车道设计制动坡床长度LZS可靠概率分别为39.55%、46.68%和54.03%,均不满足大于95%的要求。原因可能为:规范认为车辆驶入速度v最小可取100 km/h,而实际情况下车辆驶入速度v近似服从正态分布,二者之间存在一定差异。

根据可靠概率95%的要求,通过避险车道制动坡床长度的可靠度功能函数式(1),可以反算出最小安全驶入速度,计算结果见表5。

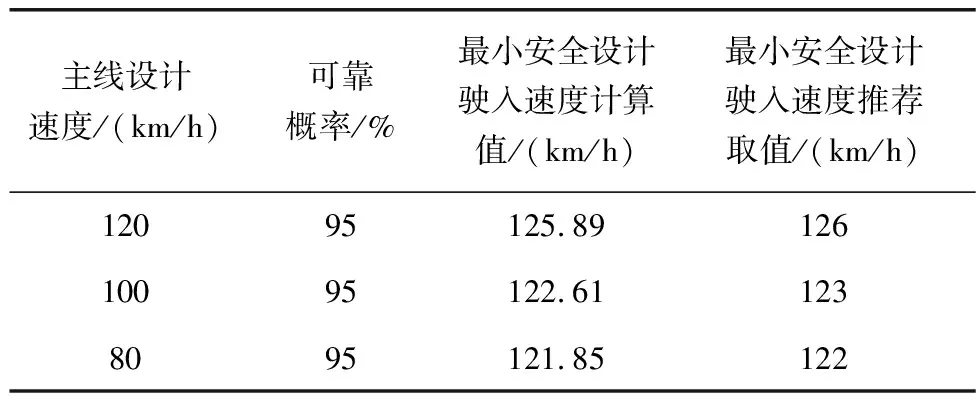
表5 驶入速度最小安全设计值与推荐选用值

表5计算结果表明,主线设计速度为120、100、80 km/h时对应的最小安全设计驶入速度推荐值分别为126、123、122 km/h,与规范要求的最小安全设计驶入速度100 km/h存在差异。由于避险车道制动坡床长度不是定值,而是根据v、f与i的设计取值综合确定,所以设计时先确定纵坡i和坡床材料f取值,再将对应的最小安全设计驶入速度推荐值代入式(3)计算得到对应的最小安全制动坡床长度。

4 工程实例

现以2条高速公路为例,湖北某高速公路项目主线设计速度为80 km/h,全长123.7 km,该路段中有一段16.9 km的连续下坡路段,高差490.1 m,平均纵坡-2.9%,最大纵坡-4.2%,总计设有4条避险车道,分布在坡中段和坡底段标号为1～4。

江西某高速公路项目主线设计速度为100 km/h。全长102.2 km。选取项目中典型的连续下坡路段,路段坡长为7.3 km,高差233.6 m,平均纵坡为-3.2%,最大纵坡-3.8%,总计设有2条避险车道,分布在坡底段,标号为5和6。

对2019—2021年这3年期间6条避险车道制动坡床内车辆发生的二次事故类型及次数进行统计,主要类型有纵向倾覆、倒溜、碰撞侧边护栏以及冲撞坡床防撞设施(制动坡床长度不足导致),分别如表6～表8。

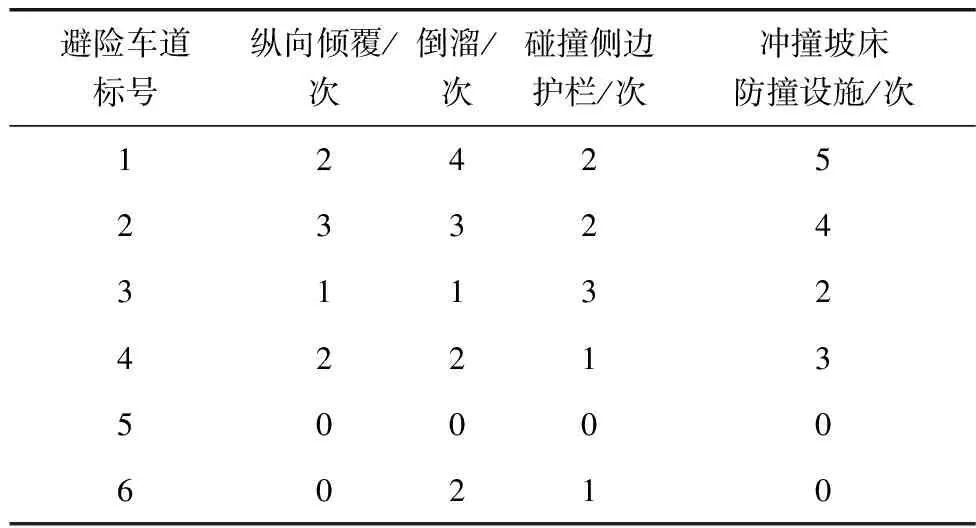
表6 2019二次事故次数汇总

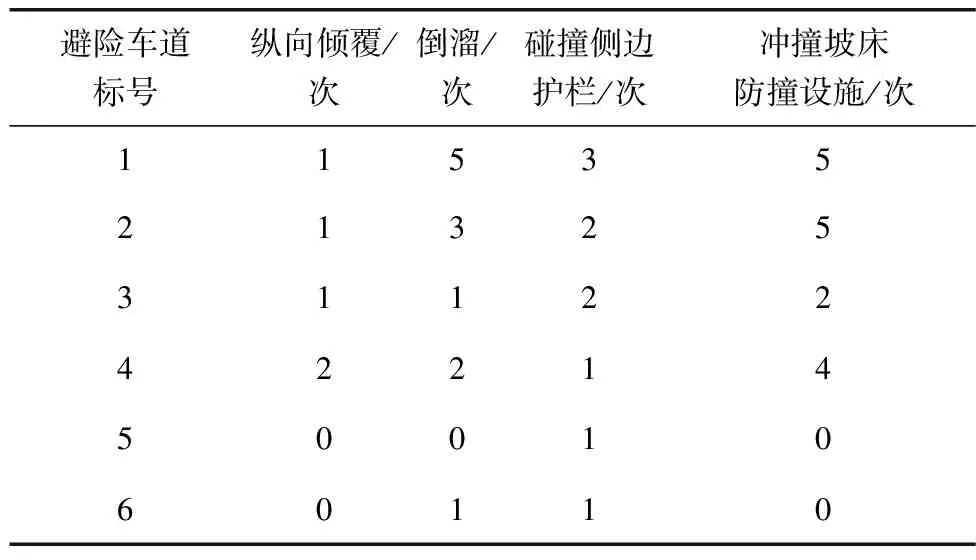
表7 2020二次事故次数汇总

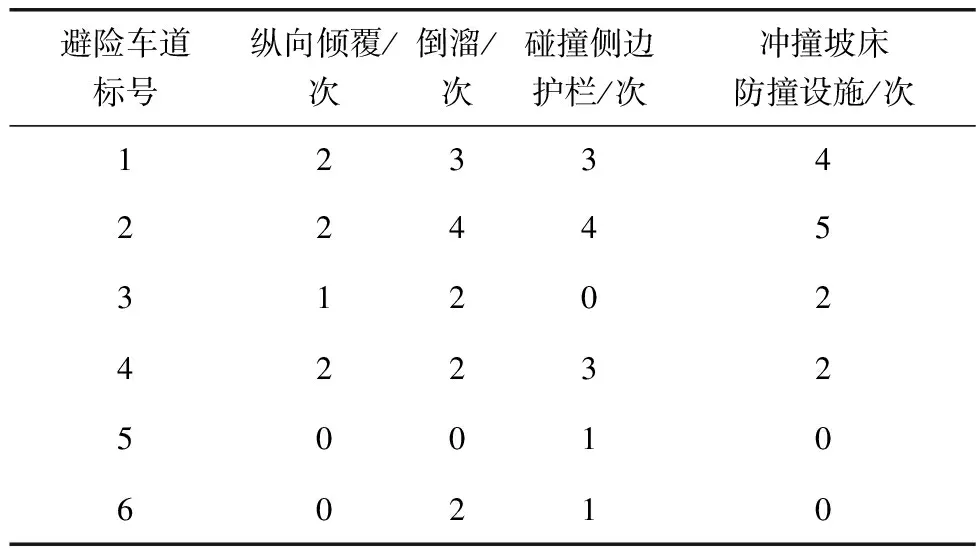
表8 2021二次事故次数汇总

由2019—2021年这3年事故类型次数可知,除5号避险车道以外,其余5条避险车道发生事故次数较多,说明避险车道没有提供足够的制动坡床长度。因此对上述6条避险车道的制动坡床长度、制动坡床坡度及材料滚动阻力系数进行统计,见表9。

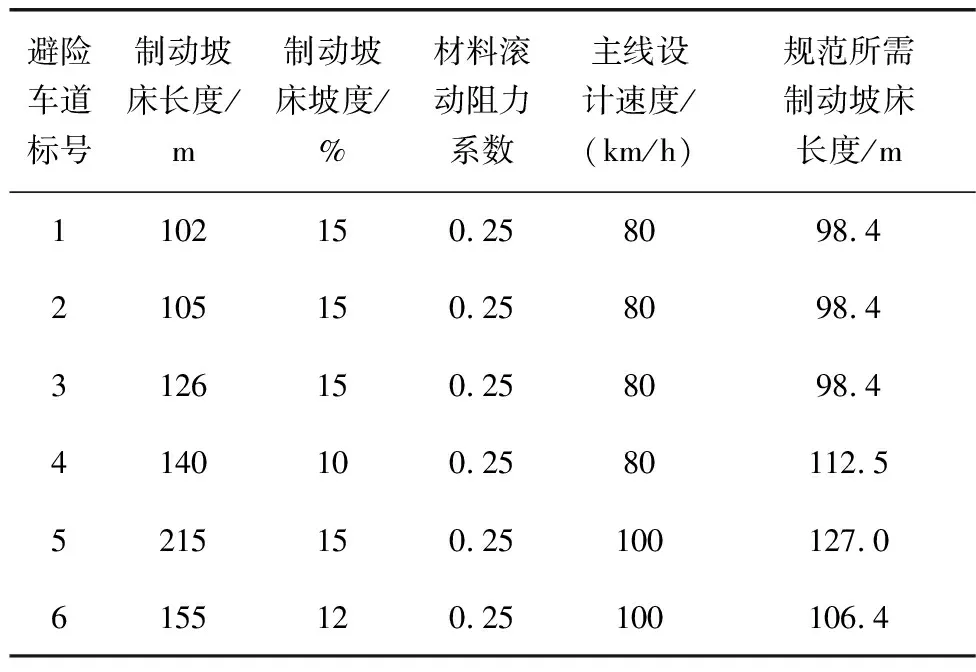
表9 避险车道制动坡床长度统计

对6条避险车道制动坡床长度实际取值进行可靠性分析,利用蒙特卡罗法计算得出其可靠概率,计算结果见表10。

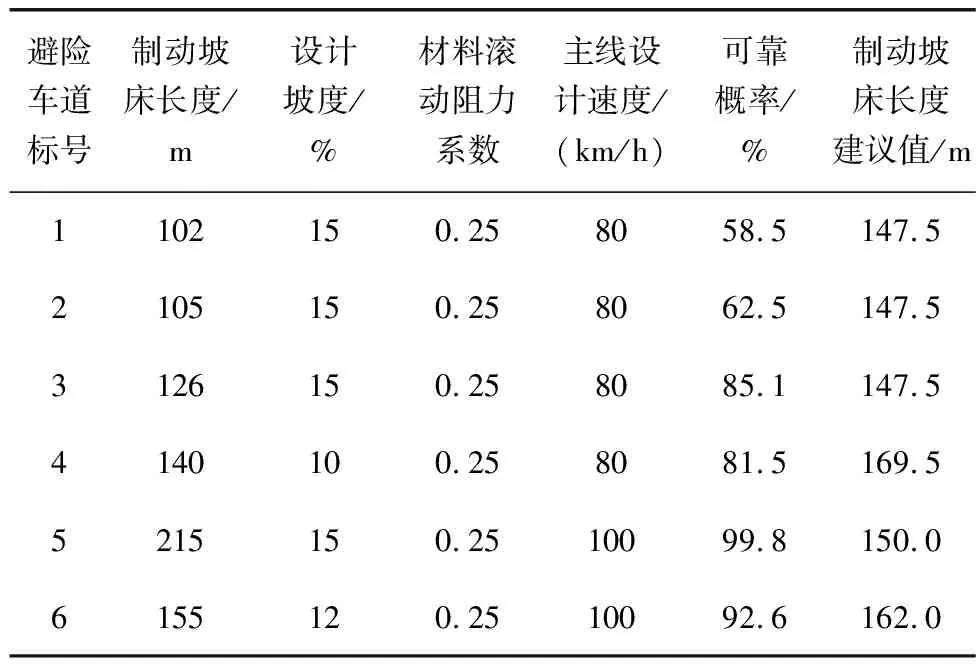
表10 避险车道制动坡床长度可靠概率计算结果

从表10中可得,1、2、3、4、6号避险车道制动坡床长度设计值的可靠概率分别为58.5%、62.5%、85.1%、81.5%、92.6%,均小于95%,不满足可靠性要求。为使得所有的避险车道均满足预期安全可靠目标,其制动坡床长度应不小于表10中的建议值,即1、2、3、4、6号避险车道制动坡床长度的设计值分别建议取为不小于147.5、147.5、147.5、169.5、162.0 m。

5 结 论

1)考虑大型车在避险车道上发生纵向倾覆和倒溜车两种极限状态,建立制动坡床长度计算模型,分析出避险车道制动坡床长度的影响因素。

2)结合可靠度理论建立制动坡床长度的可靠度功能函数,对功能函数中的驶入速度、滚动阻力系数、制动坡床坡度等参数进行分析,并利用蒙特卡罗法计算不同制动坡床长度设计值的可靠概率,得到高速公路主线设计速度为120、100、80 km/h时,避险车道制动坡床长度可靠概率分别为39.55%、46.68%和54.03%,均小于95%,表明避险车道设计的安全可靠程度不足。

3)根据高速公路一级安全等级95%可靠度要求,计算得到高速公路主线设计速度为120、100、80 km/h时制动坡床长度安全建议值由对应的最小安全设计驶入速度126、123、122 km/h与设计选取的纵坡i和坡床材料f综合计算得出。