基于声传播模拟的多孔沥青混合料吸声性能与孔结构关系

陈 俊,孙振浩,李嘉浩,2,王俊鹏

(1.河海大学 土木与交通学院,江苏 南京 210098;2.四川省公路规划勘察设计研究院有限公司,四川 成都 610041)

0 引 言

随着我国城市公路网密度持续增大,机动车保有量逐年上升,交通噪声污染问题也日益突出[1],防控交通噪声污染已成为城市治理的重要内容。在减缓城市交通噪声的技术方案(降噪路面、降噪轮胎、声屏障、行道树等)中,多孔路面具有连通孔隙丰富、与交通噪声源距离近,对噪声降低程度高(1.5～4.5 dB)[2-4]的特点,成为了各大城市降低交通噪声的重要措施。

围绕着多孔沥青混合料降噪机理,有学者分析了多孔沥青混合料空隙率、连通空隙率及结构层厚度对吸声性能的影响,认为较大的空隙率有利于吸声降噪[5-6];H.ZHANG等[7]指出过高的空隙率并不能显著提高路面降噪性能,建议空隙率控制在17%-24%;L.CHU等[8]通过ASTM 1050-10吸声系数测试,发现降低沥青混合料空隙率(由25%降至12%),将引起吸声频率的降低;B.YANG等[9]认为除了孔隙体积之外,孔径对沥青混合料吸声性能影响显著。在吸声系数预测模型方面,L.GAO等[10]利用驻波管法测得多孔混合料的吸声系数,建立了由空隙率、连通空隙率、孔隙体积等参数预估吸声系数的模型;E.GOURDON等[11]指出预估模型对空隙率高于20%的混合料适用性较差。可见,目前各个研究者结论并不完全一致,尚未完整揭示出多孔沥青混合料孔隙结构对吸声降噪的影响规律。

为此,笔者运用XCT扫描及图像处理方法,重构3种空隙率多孔沥青混合料三维孔隙结构,分析了连通孔隙曲率、长度、孔隙内壁粗糙度、孔隙横截面的面积及椭圆率等在内的形状特征;基于孔隙结构内声传播的有限元模拟,获得3种空隙率混合料的吸声系数,并分析其与孔隙形状特征的关系。

1 多孔沥青混合料三维连通孔隙

1.1 三维重构及孔隙识别

根据多孔沥青混合料配合比设计方法,设计了3种不同空隙率OGFC-13的矿料级配(表1),其中粗集料采用玄武岩,细集料和矿粉为石灰岩。通过肯塔堡飞散损失率及沥青析漏量,分别确定最佳沥青用量为4.7%、4.5%、4.4%,沥青均为5.4%SBS改性90#基质沥青。按矿料级配和最佳沥青用量,制备马歇尔试件,由蜡封法测得的空隙率分别为18.9%、20.6%、22.7%。

表1 OGFC-13混合料的矿料级配和沥青用量

采用X射线XCT扫描OGFC-13马歇尔试件,扫描参数为:120 kV电压、145 mA电流、0.625 mm扫描间隔。采用Mimics图像处理软件对扫描图像进行三维重构,如图1(a);考虑到模型尺寸对后续声传播模拟效率的影响,对重构所得试件进行切割,得到边长3 cm的立方体芯样如图1(b),其中深色部分为混合料固体(矿料和沥青)、浅色部分为孔隙〔提取后如图1(c)〕;对此总孔隙结构进行连通孔隙识别,得到图1(d)的连通孔隙。由此获得了表1中3个OGFC-13试件内部芯样的连通孔隙,用于后续孔隙结构分析和声传播模拟。

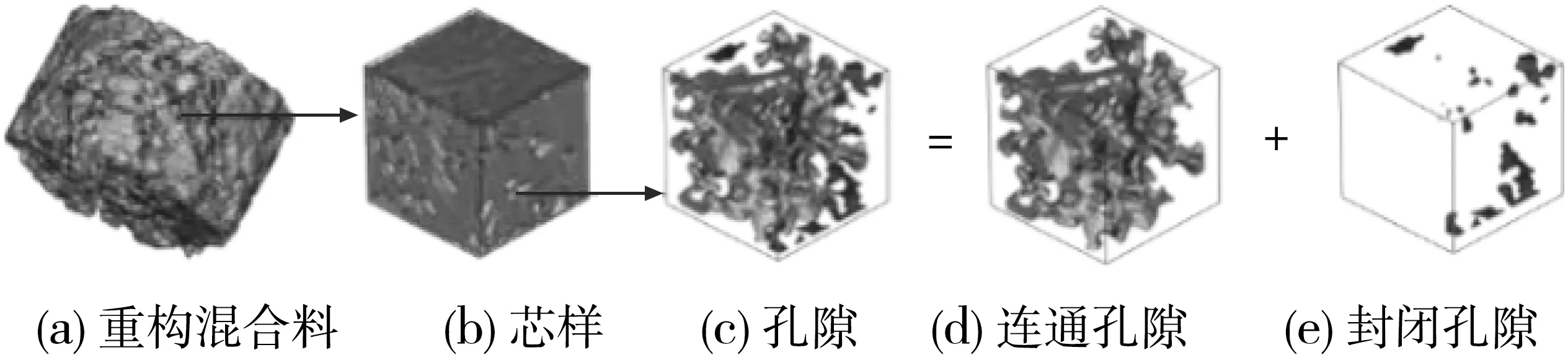
图1 混合料内连通孔隙获取过程

1.2 孔隙结构的形状指标

参照笔者已有研究成果[12-13],按图2计算连通孔隙结构指标。包括:连通孔隙长度、连通孔隙曲率、孔隙横截面面积、孔隙横截面的椭圆率、孔隙内壁粗糙度。其中,曲率为在孔隙特征点处与孔隙中轴线相切圆半径的倒数,其值越大说明连通孔隙弯曲程度越高;孔隙横截面面积是垂直于孔隙中轴线的截面面积;椭圆率为孔隙横截面当量椭圆短轴与长轴的比值;内壁粗糙度为横截面的面积与周长平方的比值,其值越小,说明孔隙内壁越粗糙。

图2 一根连通孔隙的形状指标计算方法

2 连通孔隙结构特征分析

对表1中每个级配OGFC-13分别成型3个马歇尔试件,经XCT扫描、三维重构后,对9个重构模型按第1节方法截取立方体芯样,在Mimics内计算9个芯样内连通空隙率及1.2节所述的孔隙指标。图3为9个芯样的连通空隙率rcav和连通孔隙长度。可见,在18%～23%的连通空隙率范围内,边长3 cm立方体芯样内连通孔隙总长度在980 mm以上,说明多孔沥青混合料内部连通孔隙极为丰富,拥有较长的内部孔隙通道。

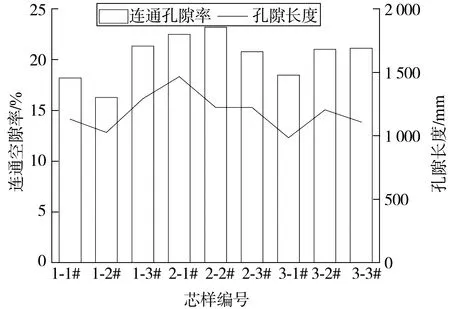
图3 不同芯样的连通空隙率及孔隙长度

从图3还可看出,连通空隙率较大的混合料,其内部孔隙长度往往较大。需要说明的是,尽管表1中3种级配马歇尔试件空隙率是:18.9%,20.6%,22.7%,但截取的芯样却与此不完全一致,这是因为孔隙在混合料内分布不均匀,而芯样的空隙率与整个试件空隙率不完全相同。

图4(a)为9个芯样的连通孔隙曲率均值。可以发现,多孔沥青混合料内部孔隙曲率均值在0.25～0.35 mm-1范围内,与图3对比,发现孔隙曲率与连通空隙率不存在明显的关系。对连通孔隙中轴线上所有特征点处的曲率频次加以统计〔图4(b)〕,可以看出,9个芯样内连通孔隙的曲率主要分布在0～0.8 mm-1范围内,尽管各个芯样连通孔隙率存在明显差别,但曲率0.2 mm-1左右的孔隙最多,可见多孔沥青混合料连通孔隙的总体弯曲程度较小。

图5、图6分别为连通孔隙横截面面积、横截面椭圆率的均值与频率的关系。连通孔隙的横截面面积主要分布在0～40 mm2之间,孔隙横截面大于40 mm2的地方很少。椭圆率主要分布在0.4～1.0之间,但0.9椭圆率出现的频次最高,达到近30%,可见连通孔隙孔径的横断面接近于圆形。

图5 不同连通空隙率时孔隙截面面积分布

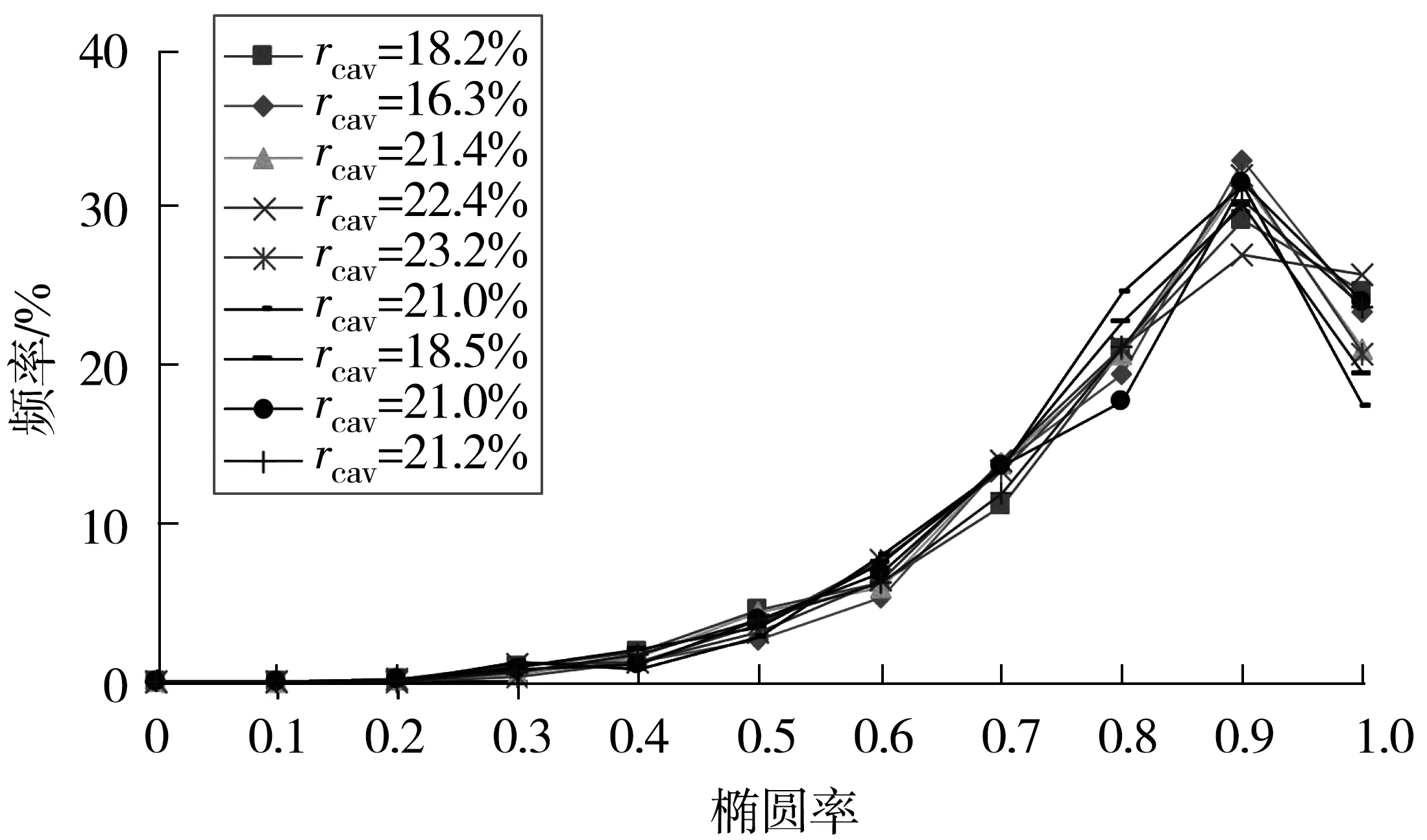
图6 不同连通空隙率下孔隙截面的椭圆率分布

对连通孔隙各特征点处的孔隙内部粗糙程度进行计算及统计,如图7。

图7 孔隙内壁粗糙度均值及分布

可以发现,试件内部粗糙度主要分布在0.04～0.06之间。从图7(b)可明显看出,连通孔隙各处的内部粗糙程度呈现“双峰”分布,第一峰范围是0.02～0.04之间,第二峰为0.07,且第二峰的频次高于第一峰。

3 多孔沥青混合料传声模拟及其验证

3.1 驻波管模拟及吸声系数计算

将图1(b)模型剔除孔隙部分,得到多孔混合料固体,如图8(a),采用COMSOL Multiphysics对其进行驻波管传声模拟。其中,管的内部尺寸为30 mm×30 mm×600 mm,管内一端为多孔混合料,另一端设置幅值为1 Pa、方向垂直于管端平面向内辐射的平面声波,声速设定为343 m/s。在空气静态压强和密度是常数,不考虑声波在稠密空气与稀疏空气交替过程中的热交换,且微小扰动在空气中引起的压强变化远小于空气的静态压强条件下,模拟频率200～3 000 Hz范围内管端平面声波在管内的传播、反射。图8(b)给出了2-2#(rcav=23.2%)、频率500、1 000、1 500 Hz下驻波管内声压级分布。

图8 驻波管传声模拟及驻波

根据驻波管内声压级分布,由式(1)计算多孔混合料法向吸声系数αp,图9为9个芯样在200～3 000 Hz每隔100 Hz下计算得到的吸声系数。为了便于分析,将声波的频段按照低频(200～1 000 Hz)、中频(1 000～2 000 Hz)、高频(2 000～3 000 Hz)划分,分别计算在3个频段内的均值及峰值,结果如表2。

表2 不同空隙率混合料吸声系数均值、峰值

图9 多孔沥青混合料吸声系数频段范围

(1)

式中:L为驻波管内声压级极大值与极小值之差,dB。

3.2 有限元模拟的验证

图10给出了文献[14]采用驻波管法实测OGFC-13和OGFC-16的吸声系数,可以看出笔者的模拟结果与实测结果在低频段处有一定差异,但在中高频率处两者比较接近。两者不完全一致的原因可能是:笔者使用的混合料级配、混合料内部孔隙形状及分布、试样尺寸与文献[14]不完全相同。考虑到笔者研究的目的是揭示孔隙形状参数对混合料吸声系数的影响规律,并不追求吸声系数模拟的绝对准确,因此可以通过有限元方法模拟声传播及计算吸声系数。

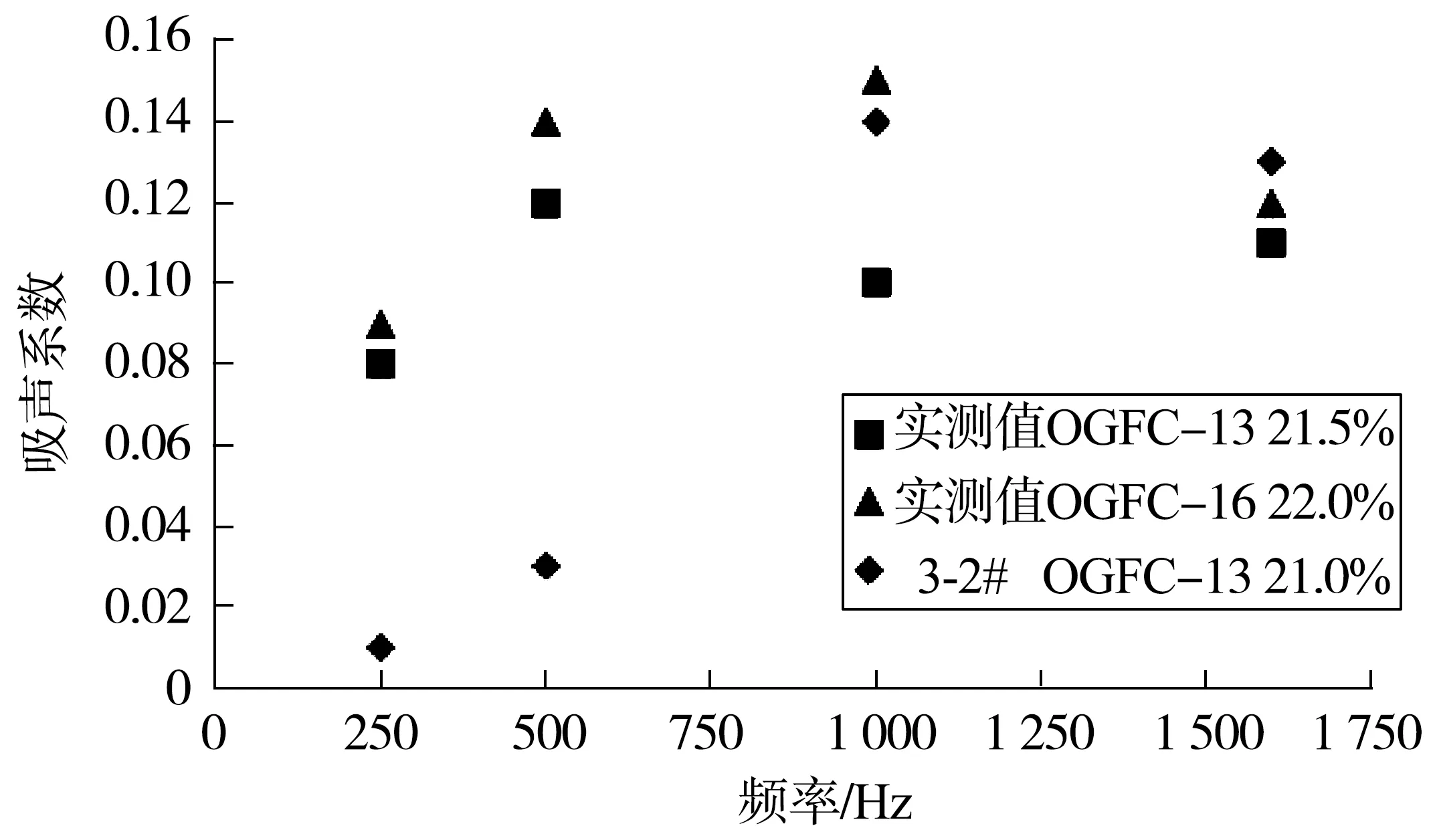
图10 吸声系数实测值与模拟结果的对比[14]

4 吸声系数与孔隙结构关系分析

对表2所列9种不同空隙率混合料吸声系数的均值、峰值,分析它们与孔隙结构的关系,图11为吸声系数与孔隙曲线、长度、横截面面积、内壁粗糙度、横截面椭圆率的拟合关系。由图11可看出,孔隙曲率、长度、横截面、椭圆率与吸声系数均值、峰值之间线性拟合的相关系数都在0.3以下,说明这些孔隙形状指标与吸声系数之间不存在明显的线性关系,通过增大或者减小这些指标不能提升多孔混合料的吸声系数。

图11 多孔混合料5种孔隙形状指标与吸声系数的关系

从图11(c)和图11(d)可以看出,尽管混合料对低频、中频声波的吸收能力与孔隙横截面大小、内壁粗糙程度依然没有明显关系,但混合料对高频声波的吸收系数与孔隙横截面的面积、孔隙内壁的粗糙度具有一定的线性关系,增大孔隙横截面或者增大内壁粗糙度可在一定程度上提高混合料对高频声波的吸收能力。

出现上述规律的原因可能是:多孔介质吸声原理是声波在孔隙内传播时,声波撞击到孔隙内壁时,声能将部分转化为热能,从而起到吸声降噪效果;当孔隙内壁越粗糙,声波撞击、反射次数越过,引起的声能衰减越多;当横截面越大时,越多的声波将与内壁接触、撞击、反射,孔隙的吸声系数越大。

5 结 论

1)多孔沥青混合料内部孔隙曲率均值在0.25～0.35 mm-1范围内,总体弯曲程度不高;边长3 cm立方体芯样内连通孔隙长度高达980 mm以上,连通孔隙极其丰富,且孔隙长度与连通空隙率具有一定线性关系。

2)多孔沥青混合料内部连通孔隙的椭圆率主要分布在0.4～1.0之间,且椭圆率0.9出现的频次最高,达到近30%,可见连通孔隙孔径的横断面接近于圆形;连通孔隙内部粗糙程度呈现“双峰”分布,说明多孔沥青混合料既有内部较光滑孔隙,也有相当比例较粗糙的孔隙壁。

3)采用有限元方法,可以实现封闭管内的声波传播和驻波模拟,并计算不同频率声波下多孔沥青混合料的吸声系数。

4)多孔沥青混合料孔隙结构与低频段、中频段吸声系数均值、峰值间无显著的线性关系,但孔隙截面面积、孔隙粗糙程度与高频段吸声系数均值、峰值具有一定的线性关系,孔隙截面面积越大,孔隙截面越粗糙,混合料对高频声波的吸收能力越强。