基于参数敏度分析的轮毂轴承寿命多目标优化

朱孙科,孙永刚,董绍江,3,蒋玉安

(1.重庆交通大学 机电与车辆工程学院,重庆 400074;2.比亚迪汽车有限公司 汽车工程研究院,陕西 西安 710119;3.重庆长江轴承股份有限公司 博士后科研工作站,重庆 401336;4.重庆交通大学 经济与管理学院,重庆 400074)

0 引 言

采用压配式内圈的第三代轮毂轴承,因集内外法兰与ABS传感器等为一体,在结构与功能上较前一代轴承更加完善,作为目前国内广泛使用的主流量产轮毂轴承,其承载能力影响着汽车的结构设计与使用寿命。针对轮毂轴承疲劳寿命开展优化研究对改善其运转性能与行驶安全性有重要意义[1]。

国内外针对轮毂轴承疲劳寿命展开的优化研究已有不少,主要通过提高轴承材料力学性能或优化轴承结构的方式实现轮毂轴承承载能力的提升,通过对比发现,优化轴承结构的方法在效率与成本上更具优势。文献[2]采用轴承额定寿命作为目标函数,对三点接触球轴承结构参数进行优化设计;文献[3]分别以额定动载荷与额定静载荷为单目标,对双列角接触球轴承进行优化设计;文献[4]以深沟球轴承与圆柱滚子轴承额定动载荷为优化目标,对两种轴承进行优化设计;文献[5]采用双目标函数即额定动静载荷对角接触球轴承进行优化研究;文献[6-7]采用三目标函数,主要针对轴承疲劳寿命、自旋摩擦功率、轴向刚度、磨损寿命与旋滚比等目标,对轮毂轴承进行优化设计,从而实现轴承承载能力的提升。可见,现有轮毂轴承优化研究大多数是针对第一代轮毂轴承进行,且大多以单目标、数学模型优化为主,优化目标的选择主要聚焦于轮毂轴承的额定动静载荷。

笔者在现有研究工作的基础上,采用数学模型优化与有限元仿真相结合的方法对某型第三代轮毂轴承疲劳寿命进行多目标优化设计,拟通过提高轮毂轴承的额定动载荷和额定静载荷,提升轮毂轴承的承载能力和抗冲击载荷能力,增加该型轮毂轴承的设计疲劳寿命。

1 多目标优化模型

1.1 目标函数

由疲劳寿命表达式(1)可知,轮毂轴承疲劳寿命与额定动载荷Cr及当量动载荷P有关。式(2)中当量动载荷P是关于轮毂轴承加载载荷的函数,与轮毂轴承尺寸参数无关。

(1)

P=fp(XFa+YFb)

(2)

式中:fp为动载荷系数;Fa和Fb分别为径向、轴向荷载,X和Y分别为径向、轴向载荷系数。

额定动载荷Cr反映轴承在某一寿命条件下承载能力大小。为提升轮毂轴承承载疲劳寿命,将额定动载荷Cr作为疲劳寿命优化的其中一个目标函数[8]。额定静载荷C的改善能增强轮毂轴承抗变形能力,减缓轮毂轴承在极限工况下发生失效的概率,因而将额定静载荷作为另一优化目标函数,额定静载荷主要分为内滚道额定静载荷Ci与外滚道额定静载荷C0,需选取两者中较小者作为优化目标。该轮毂轴承的优化设计目标可描述为:

max[C]=min[Ci,C0]=

(3)

1.2 约束条件

考虑轮毂轴承实际加工情况,轮毂轴承几何参数须满足装配与设计要求,该型第三代轮毂轴承的5个主要设计变量需满足如下约束条件[9]:

(4)

(0.5-e)(D+d)≤dwp≤(0.5+e)(D+d)

(5)

0.505≤fi≤0.525

(6)

0.515≤f0≤0.535

(7)

(8)

(9)

25°≤α≤45°

(10)

式中:D、d分别为轮毂轴承的外径与内径;kDmin和kDmax为球径约束条件系数;e为节圆直径约束系数;ε为内外圈沟底壁厚约束系数。

辅助设计变量约束条件为:0.6≤kDmax≤0.7;0.4≤kDmin≤0.5;0.03≤e≤0.08;0.3≤ε≤0.35。

1.3 轮毂轴承结构参数灵敏度分析

正交试验设计可使各影响因子水平均衡搭配,数据点分布均匀,具有均匀分散的特点,故选用正交数组进行抽样。在MATLAB中编写额定动载荷与额定静载荷计算程序,依托Isight集成调用平台,实现试验设计组件与MATLAB计算程序的调用,分析选取dw、Z、α、fi、f0、dwp共6个轮毂轴承结构参数作为变量,Cr与C为响应指标,进行灵敏度分析,问题规模为4128。

采用Pareto图表示的各变量灵敏度分析结果,如图1,各变量对响应指标的影响程度用百分占比率来表示,白色代表正效应,表示响应指标随着该变量值的增大而增大;黑色代表负效应,表示响应指标随该变量值的增大而减小;二次方代表二阶主效应,表示该变量对响应指标的影响呈现非线性,“-”代表两变量之间存在交互效应,两个设计变量共同变化时对指标的影响。

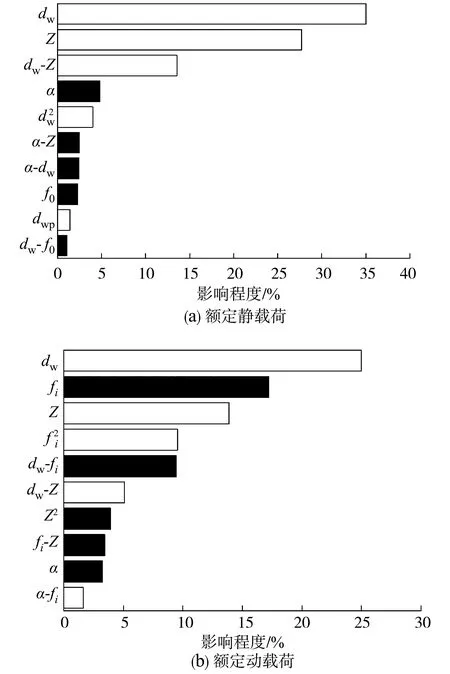
图1 轴承内部结构参数对响应指标影响的Pareto图

由图1(a)可知:对额定静载荷C起显著影响作用的正效应设计变量主要有滚珠直径dw及每列滚珠个数Z,随着滚珠直径dw的增大与滚珠数量Z的增多,额定静载荷显著增大,影响较小的正效应设计变量为节圆直径dwp,其中滚珠与内外圈接触角对额定静载荷的变化呈负效应。

由图1(b)可知:对额定动载荷Cr起显著影响作用的正效应设计变量主要是滚珠直径dw及单列滚珠个数Z,其次是内沟曲率系数的二阶效应及滚珠直径与个数的交互效应,其中内沟曲率系数fi及滚珠接触角α对额定动载荷Cr具有负效应。由灵敏度分析结果可知,滚珠直径与单列滚珠个数对额定动载荷与额定静载荷的影响最大,在轮毂轴承优化设计过程中,进行设计变量参数选取时应重点关注。

1.4 设计变量

根据灵敏度分析结果可知,接触角α的变化对目标函数的改变呈现负效应,减小接触角对改善轴承动静载荷效果并不明显,因而选取第三代轮毂轴承滚珠直径dw、节圆直径dwp、单列滚珠个数Z及内外沟道曲率半径系数fi与f05个结构参数作为多目标优化主要设计变量,kDmin、kDmax、e及、ε作为辅助设计变量,各设计参数关系如图2,采用向量如式(13)。

图2 轮毂轴承设计参数示意

X=[dw,dwp,Z,fi,f0]

(12)

表1给出了各主要设计变量原始参数值,通过以上5个主要设计参数即可得到轮毂轴承内部滚珠与滚道接触区结构。

表1 轮毂轴承主要设计变量原始参数值

2 多目标优化求解

在全局优化算法中,非支配排序遗传算法(NSGA-II)、多岛遗传算法(MIGA)和多目标粒子群优化算法(MOPSO)与其它算法相比,具有计算效率高和精英保留策略、能均匀的Pareto最优前端分布、可较好地抑制早熟现象和较强的全局搜索能力等优点。在此次优化中依托Isight优化调用平台,选用NSGA-II算法、MIGA算法和MOPSO算法等内部集成的全局优化算法进行多目标优化求解。

NSGA-II算法作为一种基于Pareto最优解的多目标遗传算法,通过采用拥挤度度量法、快速非支配排序法及精英策略改进了原算法需指定共享半径的缺陷,计算复杂度降低,提高了算法的收敛性[10]。其基本思想是:通过随机产生一个规模为N的初始父代种群p0,对其进行非支配排序,并经过选择、交叉与变异操作后形成子种群Q0;将大小为N的父代种群与大小为N的子代种群进行合并,形成规模为2N的新种群R0,再对新种群进行非支配排序,找到种群中np=0(np为种群中支配个体p的个体数)的个体将其保存至集合F中,得到m个按递减排序的非支配集Fm,对每个集中的个体进行拥挤度计算,挑选符合要求的个体组成规模大小为N的新的父代种群p1;新种群通过遗传算法的选择、交叉与变异操作生成同等规模的子种群Q1,如此往复循环选择,直到满足最大的进化代数结束运行。笔者将初始种群大小设为100,最大迭代数为60,交叉概率为0.9,最大遗传代数N取6 001。

多岛遗传算法(MIGA)特点在于将种群进行分解成为若干子种群,这些子种群被称作岛,在分解后的岛之间使用遗传算法的交叉、变异和迁移等操作使子代种群进化,从而输出最优解。相比传统遗传算法计算效率更高,全局求解能力更强。最优化粒子群优化算法(MOPSO),是一种在给定条件内根据粒子位置和速度的更新寻找更优粒子的方法,通过向最优解方向反复迭代演化从而找到一组权衡多个目标的解[11]。

依据对原型轮毂轴寿命仿真结果分析所建立的某型第三代轮毂轴承多目标优化数学模型,结合选择的优化算法,搭建的某型轮毂轴承寿命优化求解框架如图3。

图3 轮毂轴承寿命优化求解框架

根据图3在MATLAB中编写相应的优化计算程序,通过Isight优化平台求解得到Pareto最优解集参数。

3 多目标优化结果分析

通过NSGA-II算法6 001次迭代计算得到最优设计变量参数如表2。

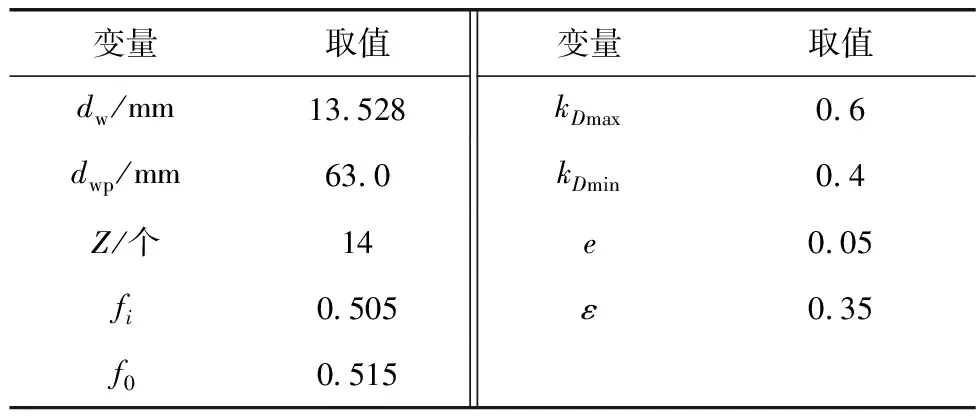
表2 NSGA-II算法优化后设计变量取值

从表2可知:该型轮毂轴承优化后得到的设计变量参数值在所给定的约束条件范围内,符合轴承装配空间及内外径壁厚设计要求。相比于原模型结构尺寸,优化后轮毂轴承滚珠数目增加、直径变大,内外沟曲率半径减小,采用NSGA-II算法优化得到的最佳额定动载荷与额定静载荷分别为125.28、170.33 kN。优化前,该型轮毂轴承的额定动、静载荷为76.20、152.08 kN,优化后额定动载荷与额定静载荷分别提高了64.4%和12.0%。额定动载荷的提升效果好于额定静载荷,与文献[3]的结论相吻合,可见以额定动载荷与额定静载荷最大化为优化目标的设计结果合理。

为验证采用NSGA-II算法对该型轮毂轴承进行优化设计的优化效果,针对式(1)～式(10),分别采用了多岛遗传算法(MIGA)与最优化粒子群优化算法(MOPSO)对该型轮毂轴承进行多目标优化求解,设计变量与目标函数值如表3。

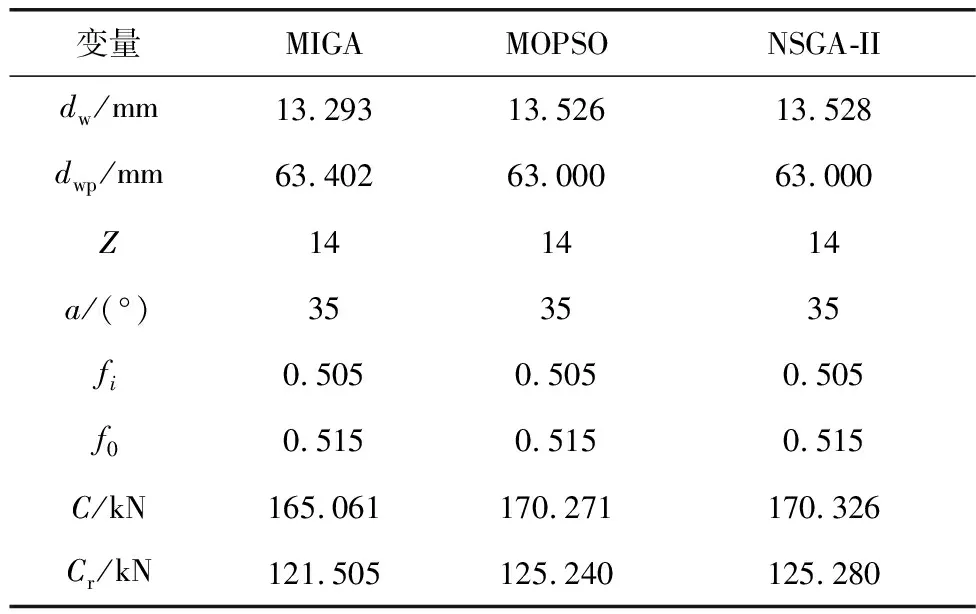
表3 采用不同优化算法优化结果对比

从表3可知:采用NSGA-II算法求解该型轮毂轴承多目标优化模型所得的优化效果最好,额定动载荷比多岛遗传算法、多目标粒子群优化算法相应结果,分别提高了3.11%、0.03%,而额定静载荷分别提高了3.20%、0.03%,可见采用NSGA-II算法求解得到的多目标优化结果,提升轮毂轴承承载能力效果更好。

4 疲劳寿命优化结果验证

4.1 轮毂轴承有限元模型

为验证第3节多目标优化设计结果的有效性,采用有限元分析分别对该型轮毂轴承初始设计和优化设计结构进行数值验证,考虑到该型轮毂轴承单元的结构复杂性,且轴承受载是以旋压铆合成形后的最终形态作为其初始状态,旋压铆合装配成形过程具有高度非线性特点,故采用显式动力学分析法对其进行模拟,其中大内圈、小内圈、滚珠和外圈采用实体单元进行模拟,对易出现应力集中区域进行网格加密处理,大内圈与外圈材料及滚动体与小内圈材料分别为65Mn钢与GCr15钢。图4给出了优化前后轮毂轴承旋压铆合仿真成形位移云图,可见,优化后旋压铆合成形三代轮毂轴承最大位移量与初设设计结构基本相吻合,最大位移仅相差约0.04 mm,优化前后误差不到1%。

图4 优化前后轮毂轴承旋压铆合成形位移云图

图5、图6为优化前后轮毂轴承轴向卡紧力与轴向游隙随时间变化曲线。

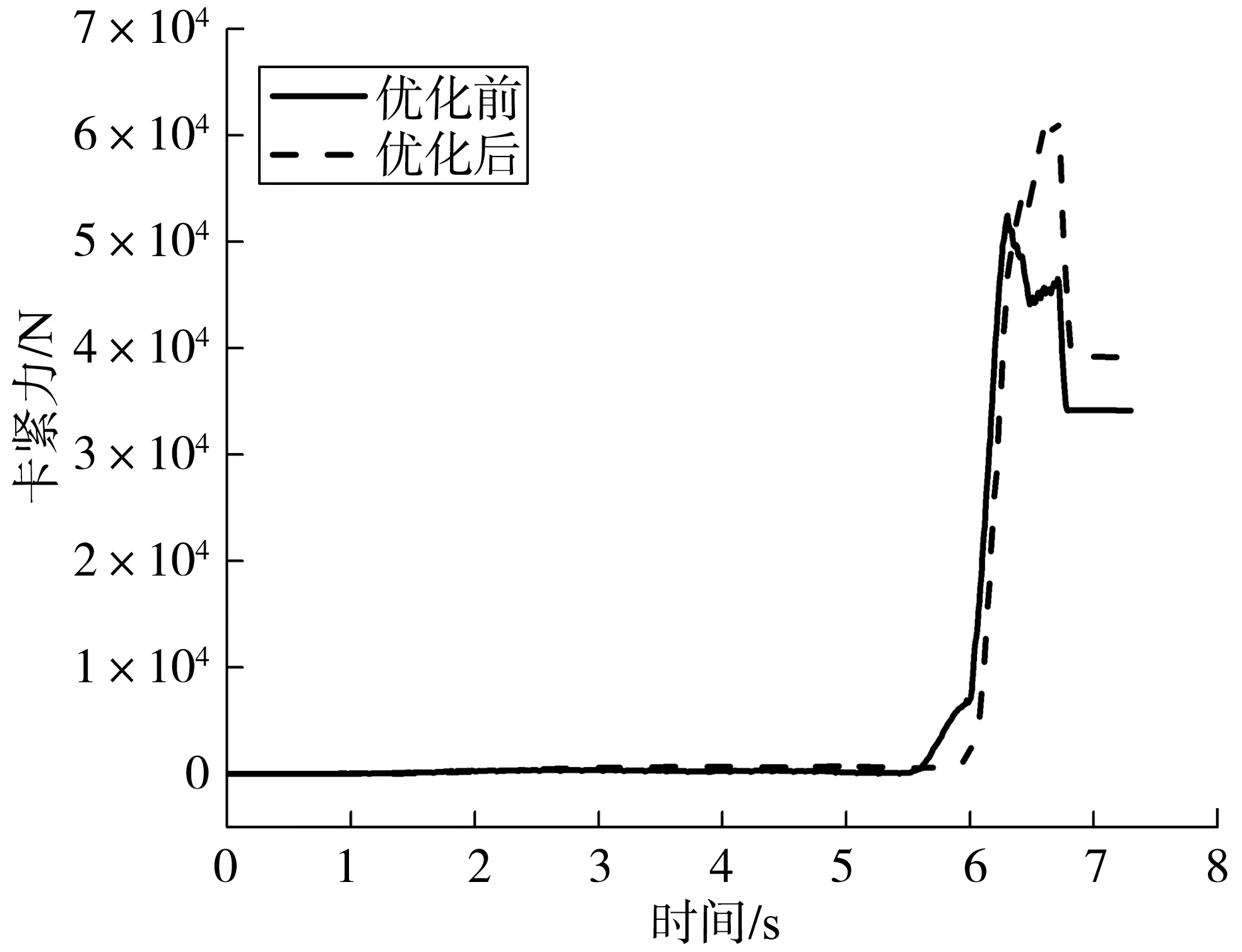
图5 轴向卡紧力随时间变化曲线

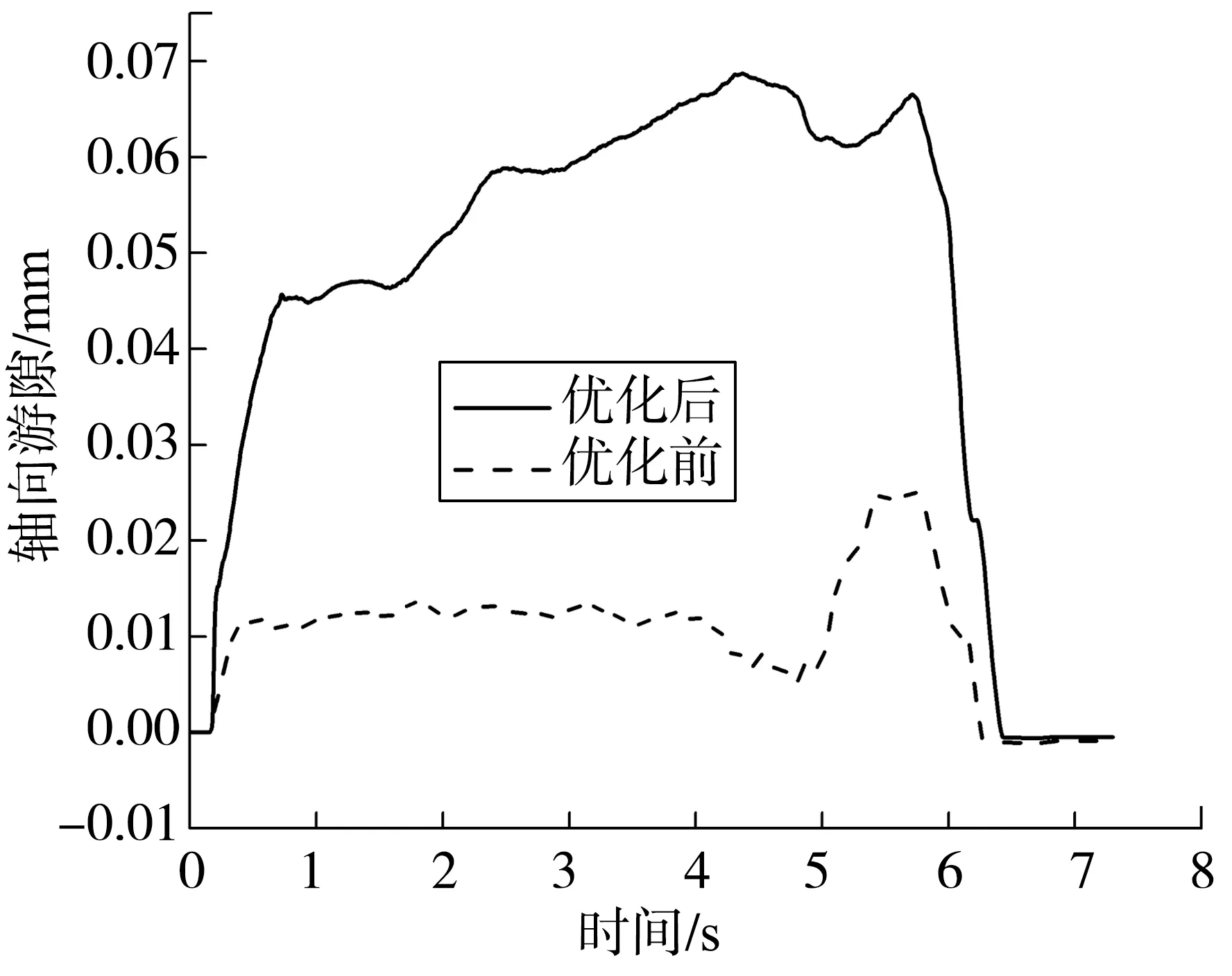
图6 轴向游隙随时间变化曲线

由图5、图6可知可知:

1)仿真初始,大内圈与小内圈轴向间隙为零,因旋铆过程中大内圈法兰盘被固定约束,随着旋铆的进行,小内圈受挤压开始上移,轴向游隙相应从零开始上升,此过程中轮毂轴承轴向卡紧力基本为零,符合大内圈变形段产生塑性变形而未与小内圈端面接触的事实;之后,大内圈变形段与小内圈端面产生接触,卡紧力明显增加,轴向游隙值也显著降低,此后,随旋压铆头上升,经回弹后轴向负游隙和卡紧力分别处于一稳定值。

2)优化前后轮毂轴承轴向卡紧力与轴向游隙曲线变化规律基本一致,优化后结构旋压铆合成形时的轴向卡紧力大于优化前轮毂轴承结构,轴向游隙小于原结构,旋压铆合成形后原结构与优化后结构轴向卡紧力分别稳定在3.416 5×104、3.910 9×104N,优化前后轴向游隙分别稳定在-8.79×10-1、-4.51×10-1μm,主要原因为优化后轮毂轴承小内圈与大内圈壁厚增加,导致小内圈与大内圈接触面积增大,单位面积所承受的压力减小。

4.2 寿命仿真结果对比

根据该型轮毂轴承实际运行与受载情况,对轴承外圈施加固定约束,并对大内圈绕轴向的转动自由度进行约束[12],在轮毂轴承中心轴线方向建立参考点,引入刚性梁约束耦合大内圈法兰盘下底面,用以施加相应的外部载荷,如图7。图8和图9给出了优化前后该轮毂轴承在0.5倍侧向加速度工况下应力云图,与优化前轮毂轴承相比,优化后轮毂轴承各组件最大应力均有所下降,如表4。

表4 优化前后轴承仿真结果对比

图7 轮毂轴承疲劳加载示意

图8 优化前轮毂轴承各组件应力云图

图9 优化后轮毂轴承各组件应力云图

图10给出了优化前后轮毂轴承中滚珠疲劳寿命分布云图。分析表4、图8、图9、图10可知,模型最大等效应力与最小疲劳寿命所在区域位于滚珠与内圈接触部位,优化后模型整体最大应力较原模型下降约5.1%,其中,内法兰盘大内圈最大应力较原部件下降约4.9%,小内圈最大应力较原部件下降约10.5%,法兰盘外圈滚道处最大应力较原部件下降约17.6%,轮毂轴承疲劳寿命从1.06×105个循环提升到1.10×105个循环,整体寿命增加了约3.8%。该有限元模型仿真计算结果验证了笔者疲劳寿命优化方案的有效性。

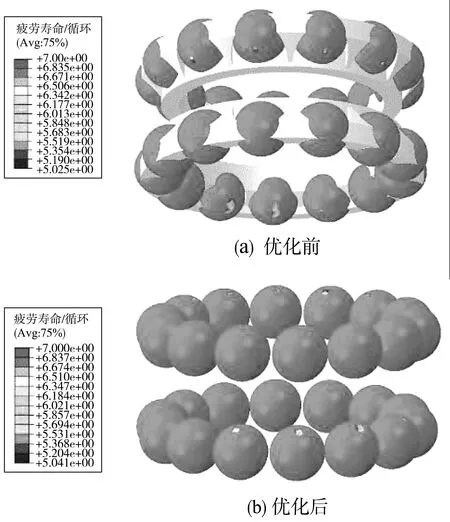
图10 优化前后轮毂轴承中滚珠疲劳寿命分布云图

5 结 论

针对某型第三代轮毂轴承疲劳寿命优化问题,通过采用正交试验设计进行灵敏度分析,得到影响轮毂轴承疲劳寿命的主要设计变量,采用轴承寿命理论计算模型建立以额定动载荷和额定静载荷为目标函数的多目标优化模型,利用多目标求解算法对其进行求解,并对轮毂轴承多目标优化设计结果进行了实车交变受载下的疲劳寿命有限元仿真验证,主要研究结论有:

1)通过对轮毂轴承额定动载荷与额定静载荷响应指标进行灵敏度与主效应分析,表明滚珠直径与单列滚珠个数对轴承性能影响最大,响应指标随着滚珠数量的增加与直径变大明显提升,在进行轴承优化参数选取时应重点关注。

2)在同等种群规模下,NSGA-II算法求解得到的最优解的性能提升效果优于MIGA算法和MOPSO算法,优化后该轮毂轴承的额定动载荷与额定静载荷相比于优化前分别提高了64.4%和12.0%;

3)对优化前后轮毂轴承实际受载条件下的疲劳寿命进行有限元分析,表明优化后结构最大应力下降了5.1%,疲劳寿命较初始设计结构提升了3.8%,验证了轮毂轴承多目标优化设计的有效性。