钻芯法检测薄壁预制构件混凝土抗压强度的试验研究*

李雪雪, 孙 彬, 毛诗洋, 张晋峰

(中国建筑科学研究院有限公司，北京 100013)

0 引言

随着装配式混凝土建筑的大规模建设,兼具模板作用的薄壁预制混凝土构件的应用越发广泛。混凝土强度是评价预制混凝土构件质量的重要指标,但受限于检测条件和工程经验,薄壁预制构件的混凝土强度主要通过检测同条件养护试块来确定,而针对其实体混凝土强度的有效检测手段相对匮乏。钻芯法被普遍认为是一种直观可靠的检测实体混凝土抗压强度的方法,但通常情况下薄壁预制构件的厚度在50～70mm之间,钻取的芯样试件尺寸不满足《钻芯法检测混凝土强度技术规程》(JGJ/T 384—2016)[1]相关要求。因此,开展小尺寸芯样试件钻芯法检测薄壁预制构件混凝土抗压强度的试验研究十分必要。

现有研究[2]表明,几何尺寸和骨料粒径是影响芯样试件抗压强度试验结果的关键因素。Bungey J H[3]和Bartlett F M等[4]研究表明,超小直径芯样试件抗压强度受其直径和骨料最大粒径比值影响比标准芯样试件更明显。高红旗[5]通过试验研究表明,芯样试件直径在50mm以上且其与最大骨料粒径之比大于1.5时,芯样试件直径对抗压强度试验结果无明显影响,但小芯样试件强度的离散性偏大,直径50mm芯样试件强度的变异系数甚至达到26.7%。李翀[6]进行了超小直径芯样检测混凝土抗压强度的试验研究,结果表明,直径50mm芯样试件与直径100mm标准芯样试件的抗压强度平均值基本相当,建议芯样试件直径与骨料最大粒径之比宜不小于2。吴体等[7]和周明华等[8]开展的试验研究表明,当芯样试件直径和骨料最大粒径之比不小于2时,小直径芯样试件强度变异系数均小于15%,采用小直径芯样试件检测混凝土强度的方法切实可行,但取样数量需相应增加。

根据调研统计结果,薄壁预制混凝土构件中的粗骨料粒径一般在10～20mm之间。基于上述实际情况,本文在满足芯样试件尺寸和骨料最大粒径之比不小于2的前提下,同时考虑高径比小于1的情况,加工制作了不同设计强度的小尺寸芯样试件和标准芯样试件进行抗压强度试验,研究建立小尺寸芯样试件与标准芯样试件的抗压强度换算关系并建议芯样试件的最小合理取样数量,以期为采用小尺寸芯样试件检测薄壁预制构件混凝土抗压强度提供数据支撑和技术依据。

1 试验概况

1.1 试件设计

1.2 试件加工制作

为获得芯样试件,首先进行预制混凝土板制作,平面尺寸为2.0m×2.0m,板厚为200mm,预制板标准养护14d后,其同条件试块抗压强度达到设计要求,在板上钻取不同直径的芯样,钻取后的芯样均在同条件下进行自然养护。试验前对芯样进行切割加工,采用硫磺胶泥补平端面,并测量最终获得的芯样试件尺寸,加工后的部分芯样试件见图1。

图1 加工后的部分芯样试件

1.3 抗压强度试验

按照《混凝土物理力学性能试验方法标准》(GB/T 50081—2019)[9],根据芯样试件压碎的预估极限荷载,分别采用微机控制电子万能试验机(最大量程100kN)和微机控制电液伺服万能试验机(最大量程1 000kN)以0.5MPa/s的加载速率对芯样试件连续加载,直至试件达到极限荷载压碎。

2 试验结果与分析

2.1 试件破坏形态

试件破坏过程如图2所示。小尺寸芯样试件和标准芯样试件从开始加载至试件表面出现竖向裂缝前,荷载与位移基本呈线性增长关系;当试件表面开始出现竖向裂缝时(图2(a)),荷载增长速率显著放缓且裂缝发展迅速,随后3～5s内试件达到极限状态,表层混凝土被瞬间压崩(图2(b)),试件开裂时的荷载及位移与极限状态时的十分接近,呈明显的脆性破坏特征。

图2 试件破坏过程

试件破坏形态如图3所示。由于钢制压板与芯样试件端面间摩擦力导致的“环箍效应”[10]从芯样试件两端至芯样试件中部逐渐减弱,DH50芯样试件和DH100标准芯样试件均呈正倒相接的圆锥体破坏形态,两端锥角均在50°左右,如图3(a)、(b)所示。D70H50芯样试件亦呈正倒相接的圆锥体破坏形态,但两端锥角大约为80°,明显大于前述DH50芯样试件和DH100标准芯样试件,如图3(c)所示,这是由于在该高径比条件下,试件上下端部的“环箍效应”在试件中部叠加,限制试件中部表层混凝土的横向变形所致。

图3 不同尺寸芯样试件破坏形态

2.2 抗压强度试验结果

2.2.1 抗压强度统计特征

芯样试件抗压强度的平均值、标准差和变异系数见表3。为得到小尺寸芯样试件的抗压强度概率分布函数,对C20-DH50-28d芯样试件抗压强度结果进行了统计分析和概率分布拟合,直方图及拟合结果见图4。为验证该组芯样试件抗压强度是否符合正态分布,利用分布族的χ2拟合检验法对其试验结果进行假设检验。取显著性水平α=0.05,其中原假设H0:C20-DH50-28d芯样试件抗压强度概率分布服从正态分布。该假设检验的拒绝域为:

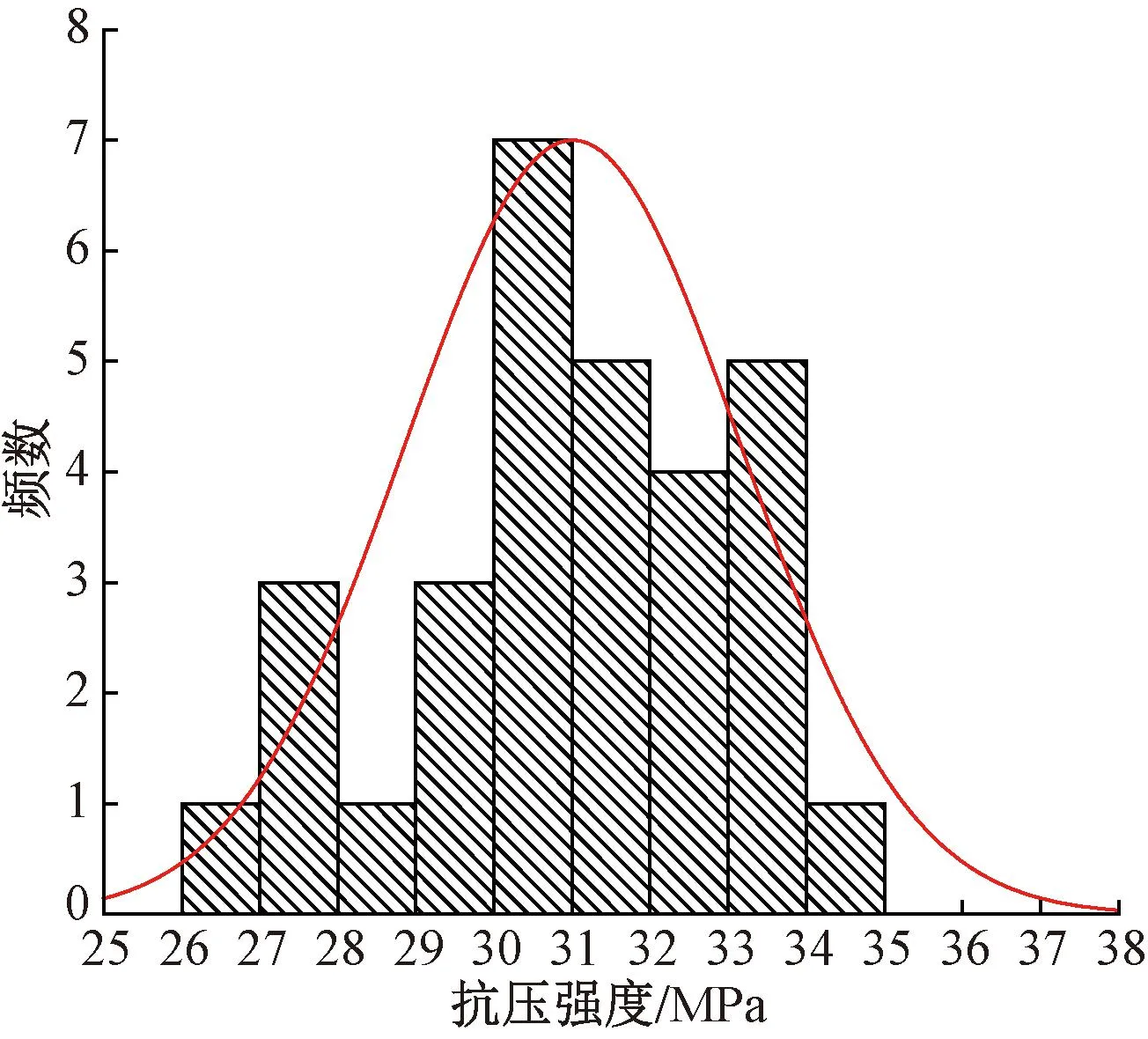
图4 C20-DH50-28d芯样试件抗压强度直方图

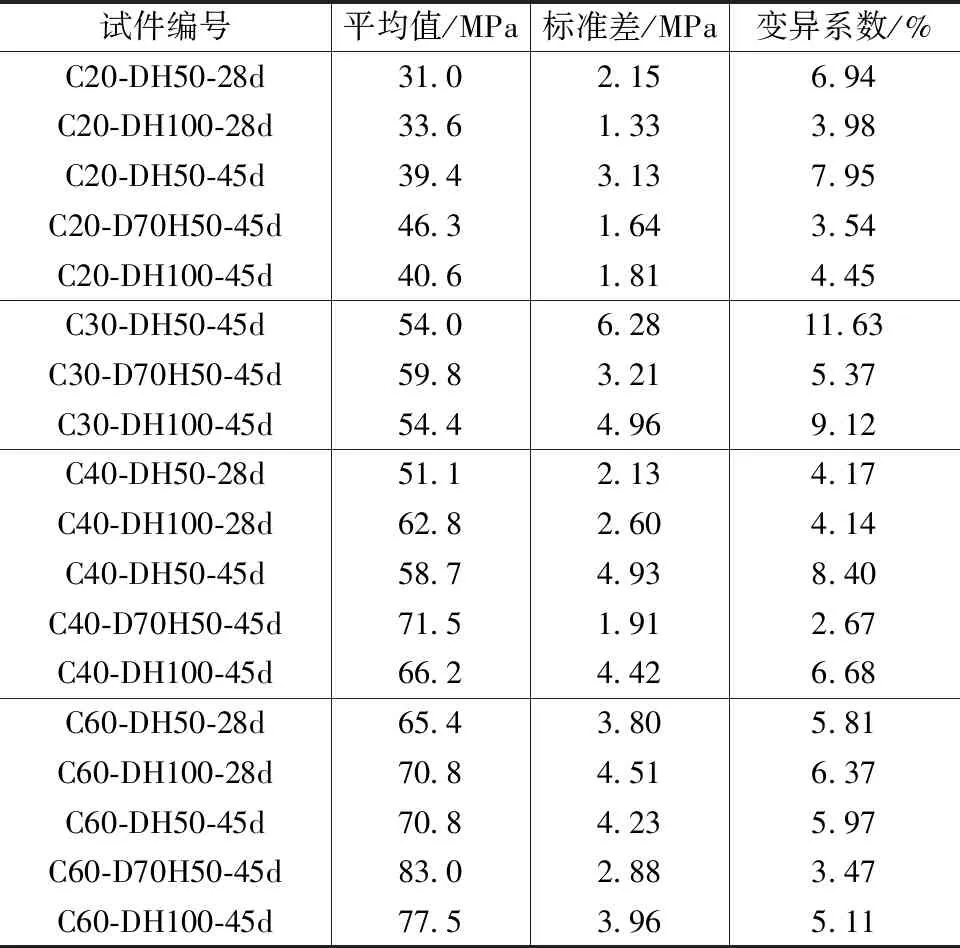
表3 芯样试件抗压强度统计汇总

(1)

(2)

式中:fi为落在各强度区间内的试验结果的个数;pi为按照假定概率分布计算得到的概率估计值;n为样本总量;r为参数估计的个数。

供应链上的一些相关事务，例如计划、采购、生产、物流等流程，大多数都是通过权威机构进行的“中心化”的设计与管理。这些权威机构就如平时生活中的银行、支付宝，被人们所信任，但是如果出现内部人员的恶意操作，导致的后果也是不可估计的。

在验证DH50芯样试件抗压强度值概率分布服从正态分布的基础上,分别将DH50、D70H50芯样试件和DH100标准芯样试件的抗压强度值进行归一化处理,再对其进行概率统计分析。结果显示,在显著水平α=0.05下,这三种芯样试件也均服从正态分布,其直方图及拟合结果见图5,由此可知,消除不同样本组的强度差异后,DH50、D70H50和DH100三种芯样试件的抗压强度值均较好地服从正态分布。

图5 芯样试件抗压强度归一化值直方图

2.2.2 芯样试件尺寸对其强度的影响分析

典型试件抗压强度平均值对比见图6。由图6可见,在高径比均为1.0的条件下,DH50芯样试件抗压强度较DH100标准芯样试件降低了0.68%～11.35%;高径比0.71的D70H50芯样试件抗压强度较DH100标准芯样试件提高了7.0%～14.0%,较DH50芯样试件提高了10.6%～21.8%,这是由于高径比减小后,“环箍效应”对试件裂缝发展的限制作用增强,从而提高了试件的抗压强度。

图6 不同尺寸芯样试件抗压强度平均值

典型试件抗压强度变异系数对比见图7。由图7可见,DH50芯样试件抗压强度变异系数均高于DH100标准芯样试件,尺寸较小试件的试验结果更易受粗骨料尺寸大小和试件加工精度等因素的影响;与文献[5]中直径50mm芯样试件抗压强度变异系数对比,本次试验DH50芯样试件强度变异系数显著降低,芯样试件直径和骨料最大粒径之比不小于2的科学性得到了验证;高径比0.71的D70H50芯样试件抗压强度变异系数小于DH100标准芯样试件,数据离散性最小。

图7 不同尺寸芯样试件抗压强度变异系数

2.3 抗压强度换算关系

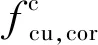
利用最小二乘法,分别采用线性函数、对数函数、多项式函数和幂函数四种函数形式进行数据拟合和回归分析,得到DH50、D70H50芯样试件抗压强度与DH100标准芯样试件抗压强度的拟合曲线(图8)。由表4可见,DH50芯样试件强度对应的5条拟合曲线中,曲线DH50-2的相关性较好,拟合效果最优;D70H50芯样试件强度对应5条拟合曲线的相关系数R2值接近,拟合效果均较好。根据两种芯样试件抗压强度的物理意义,拟合曲线应经过坐标原点,故曲线D70H50-1、D70H50-3和D70H50-4对应的拟合公式不符合要求。

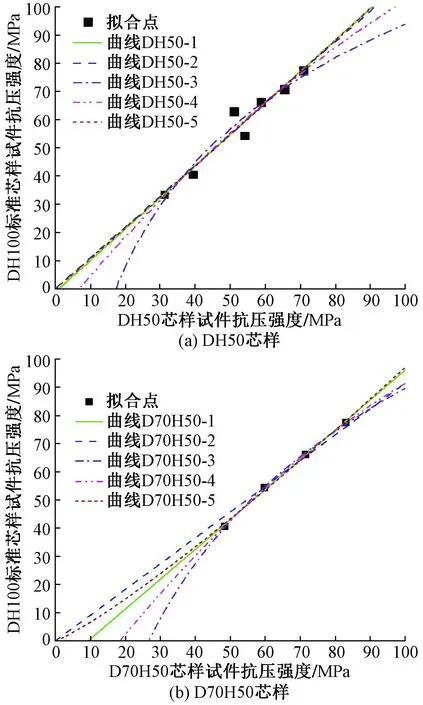
图8 芯样试件抗压强度拟合曲线图

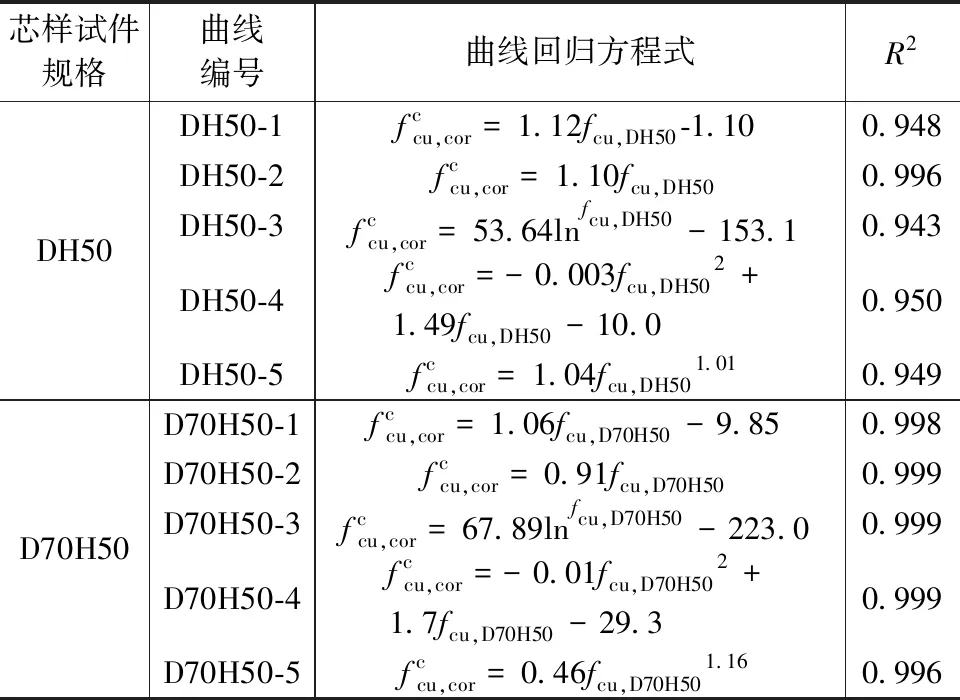
表4 不同芯样试件强度回归曲线分析汇总

通过对拟合效果和拟合曲线趋势的综合分析,建议钻取DH50芯样试件和D70H50芯样试件检测薄壁预制构件混凝土抗压强度的换算关系均采用线性关系,即:

(3)

(4)

2.4 最小取样数量确定

在对混凝土抗压强度进行区间推定时,需要控制推定区间上下限差值。《钻芯法检测混凝土强度技术规程》(JGJ/T 384—2016)[1]中规定:当采用小直径芯样试件时,置信度可为0.85,错判概率不大于0.05,漏判概率不大于0.10,推定区间上下限的差值不宜大于5.0MPa和0.10fcu,cor,m两者中的较大值,即:

fcu,e1-fcu,e2=(k2-k1)s≤max{5.0,0.10fcu,cor,m}

(5)

(1)当抗压强度平均值不大于50MPa时,推定区间宽度由5.0MPa控制,由式(5)得到:

s≤[sm]=5.0/(k2-k1)

(6)

(2)当抗压强度平均值大于50MPa时,推定区间宽度由0.10fcu,cor,m控制,由式(5)得到:

δ=s/fcu,cor,m≤[δm]=0.10/(k2-k1)

(7)

式中:fcu,cor,m为芯样试件抗压强度平均值,MPa;fcu,e1为混凝土抗压强度推定上限值,MPa;fcu,e2为混凝土抗压强度推定下限值,MPa;k1、k2分别为推定区间上限值系数和下限值系数,与芯样试件数量有关[11];s和[sm]分别为芯样试件抗压强度的标准差及其允许值,MPa;δ和[δm]分别为芯样试件抗压强度的变异系数及其允许值。

由式(6)和式(7)可见,取样数量与样本的标准差或者变异系数有关。本文提出采用模拟抽样的方式,以m为起始(m=5, 6, 7…n)在数量为n的样本中进行随机抽样,可获得不同样本容量m下芯样试件抗压强度标准差最大值sm,max和变异系数最大值δm,max,同时计算不同样本容量对应的[sm]和[δm],从而确定合理的芯样试件数量。

分别以C20-DH50-28d、C20-D70H50-45d芯样试件的试验结果为例,通过模拟抽样,确定钻取DH50芯样试件和D70H50芯样试件的合理取样数量。按照式(3)、(4)换算后,两种芯样试件混凝土抗压强度换算值的标准差最大值和变异系数最大值与样本容量的关系见图9、10,同时计算出其允许值与样本容量的关系。

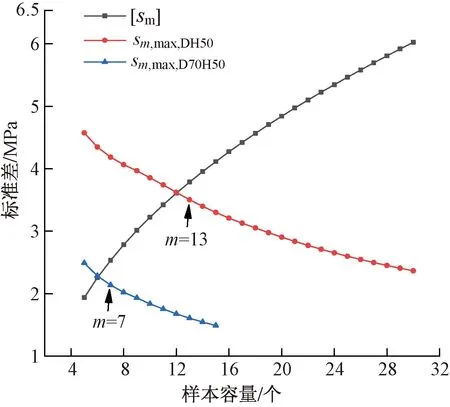
图9 不同样本容量下对应的强度标准差

由图9可见,当取样数量不低于13时,C20-DH50-28d芯样试件的标准差最大值均小于[s13];当取样数量不低于7时,C20-D70H50-45d芯样试件的标准差最大值均小于[s7]。由图10可见,当取样数量不低于18时,C20-DH50-28d芯样试件的变异系数最大值均小于[δ18];当取样数量不低于9时,C20-D70H50-45d芯样试件的变异系数最大值均小于[δ9]。因本次试验芯样试件强度均值小于50MPa,故按照式(7)控制变异系数确定的取样数量偏于严格。本次试验芯样试件的代表性和数量均有限,仅为了验证模拟抽样方法的可行性。当数据统计量达到一定规模,掌握了较为可靠的小尺寸芯样试件变异系数后,建议按照控制变异系数的方法确定取样的最小数量。

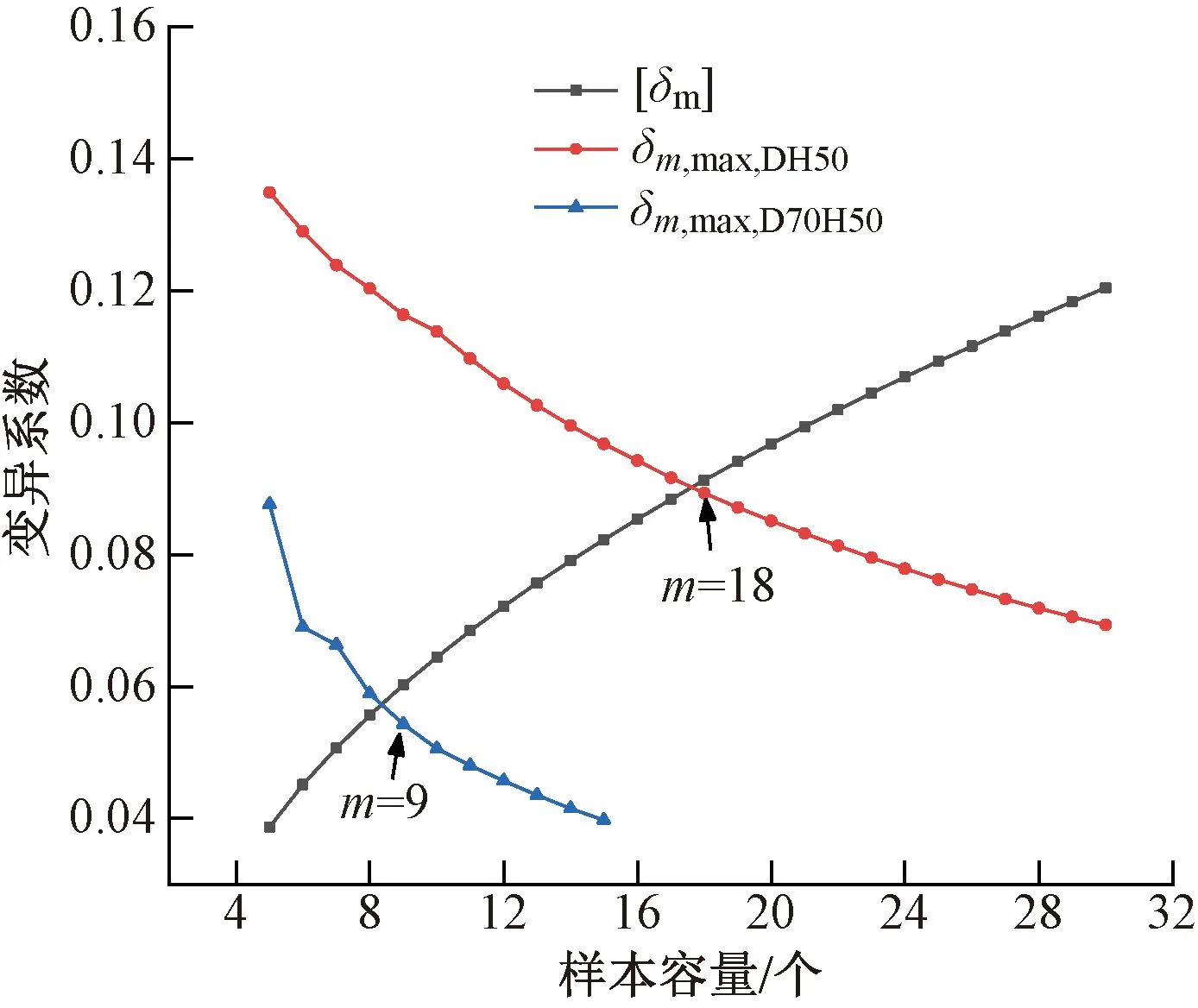
图10 不同样本容量下对应的强度变异系数

根据《钻芯法检测混凝土强度技术规程》(JGJ/T 384—2016)[1]可知,直径100mm芯样试件数量不宜少于15个,小直径芯样试件数量不宜小于20。可见,本次模拟得到的取样数量明显小于标准要求。实际工程存在诸多不确定因素,基于D70H50芯样试件强度离散性较DH100标准芯样试件小,并考虑到与现行标准相一致,建议D70H50芯样试件取样数量不宜少于15个,DH50芯样试件取样数量不宜少于21个。

3 结论

以薄壁预制构件实体混凝土强度为研究对象,采用钻芯法对小尺寸芯样试件和标准芯样试件的混凝土抗压强度进行了试验研究,得到以下结论:

(1)小尺寸芯样试件与标准芯样试件均呈正倒相接的圆锥体破坏形态,但在钢制压板与芯样试件端面间摩擦力导致的“环箍效应”影响下,D70H50芯样试件破坏时两端锥角大约为80°,明显大于DH50芯样试件和DH100标准芯样试件。

(2)根据芯样试件抗压强度统计结果,DH50芯样试件、D70H50芯样试件和DH100标准芯样试件的混凝土抗压强度值均服从正态分布;相比DH50芯样试件和DH100标准芯样试件,D70H50芯样试件的抗压强度值最大,抗压强度离散性最小。

(3)通过最小二乘法及拟合效果分析,DH50和D70H50芯样试件的抗压强度与DH100标准芯样试件的抗压强度可采用线性换算关系;提出通过模拟抽样方法确定DH50和D70H50芯样试件的最小合理取样数量,建议数量分别为21个和15个。

(4)综合考虑DH50和D70H50芯样试件的抗压强度拟合效果和取样经济性,建议钻取高径比0.71的D70H50芯样试件检测薄壁预制构件的混凝土抗压强度。