多孔介质结构对储层内流动和换热特性的影响
汪健生,张辉鹏,2,刘雪玲,2,傅煜郭,2,朱剑啸,2
(1 中低温热能高效利用教育部重点实验室,天津大学,天津 300350;2 天津大学机械工程学院地热研究培训中心,天津 300350)
近年来全球能源格局转型加快,清洁能源利用比例不断提高,为解决可再生能源系统在时间和空间上的不匹配特性[1],储能技术越来越受到重视。地下储层受大气环境波动的影响小,温度恒定,是一种优良的储能场所[2-3]。由于含水层储能的存储容量高且成本低,利用含水层进行季节性的储能已在国内外受到广泛关注。对含水层储能的研究主要集中于宏观尺度下储能系统的热提取性能,研究者利用均质化模型获得储层的平均换热和流动参数。Ganguly等[4]模拟计算了均质含水层内的瞬态温度分布,分析了不同流量下的热提取量。Liu等[5]研究了回灌水温和孔隙度对储层内换热特性的影响,发现孔隙率的影响很大。Ghaebi 等[6]针对一含水层住宅供暖项目,研究了储能系统在不同运行方案下的热回收系数。Jiang等[7]改进了抽灌井的过滤结构,研究发现半过滤井结构能够减缓热突破,提高传热系统的性能系数。但由于含水层储能对地下环境要求高且可能造成地下水污染,其利用和发展受到限制。通过构建人工储层,可降低对选址的要求,并减小对地下环境的污染。人工储层内的填充结构是影响系统性能的关键因素。
目前对人工构建地下多孔介质储层的储能研究和利用尚不多见。但是在化工工业中,研究人员通过优化填料床内的颗粒填充形状和填充方式提高换热效率,加快反应。Calis等[8]模拟了不同粒径催化剂颗粒填充层内空气的流动特性,发现管径和颗粒直径比低的填料床压降更小。Alkhalaf 等[9]研究发现颗粒间存在间隙或颗粒重叠时,由于颗粒间的接触方式不同,影响填料床内流体的交叉混合,进而影响传热效果。Gunjal 等[10]比较了4 种不同堆积方式的周期性球体阵列中的流动和传热特性,发现了颗粒排列形式的影响较大。Qi等[11]针对非等温流体的模拟研究,发现填料床的孔隙率是影响流体流动和传热的重要因素。考虑到随机填料床内流体的压降远高于结构填料床,Yang等[12]对比研究了均匀和非均匀填料床内的流动和换热特性,发现选择合适的填料形式和颗粒形状,可以显著降低压降,提高结构填料床的整体传热性能。Fu等[13]实验研究了非均质多孔介质内的流动传热特性,结果表明局部孔隙的差异是造成流体渗流和传热差异的主要原因。Halkarni 等[14-15]通过实验得到了不同粒径床层的体积对流传热系数,发现采用粒径小的颗粒填充,可提高多孔介质内的体积传热系数。Aksornkitti 等[16]研究了热水在二维颗粒填料床入渗过程中的热湿传递特性,发现流量和粒径对温度的影响较大。以上的研究主要集中在球形颗粒填充的多孔介质内的流动和传热性能的研究,表明填充颗粒的粒径、颗粒间间隙以及堆积方式,对多孔介质内的流动和传热都有较强的影响。对颗粒的几何形状发生变化后,填充多孔介质内的流动和传热性能的研究较少。通过构建人工储层进行地下储能时,采用球形颗粒填充的储层蓄水能力较小。为了综合考虑储层的传热特性及蓄水能力,有必要对非结构化的颗粒填充的多孔介质内的流动和传热特性进行探究。为此,构建了非均匀颗粒、十二面体梯度开孔和二十面体梯度开孔的3 种填充颗粒结构,采用共轭传热模型,对填充不同颗粒结构的多孔介质通道代表性体积单元内的流动和换热进行了数值模拟,获得不同填充结构下的对流传热系数和渗流性能,并对其流动和传热特性进行综合评价。通过研究可为人工储层的构建提供适合的填充物结构,为人工储层内流体和固体骨架间的对流换热表面传热系数的确定和选取提供可参考的数据。
1 数值模拟过程
1.1 物理模型
地下含水层储能通常采用双井系统,回灌井与生产井周围的储层结构直接影响含水层的储能效率和热提取效果。本研究基于界面表面积密度和孔隙率差异分别构建了3 种多孔介质,即非均匀颗粒、十二面体梯度开孔和二十面体梯度开孔(图1)。其中图1(a)填充的非均匀颗粒包括球形以及椭球形,颗粒半径分布在0.5~0.6mm 之间,图1(b)和(c)中分别填充边长均为1mm 的十二面体与二十面体开孔结构,沿着渗流方向孔径递减。3种多孔介质填充通道的几何尺寸见表1。多孔介质骨架为岩石,其热物性参数见表2。
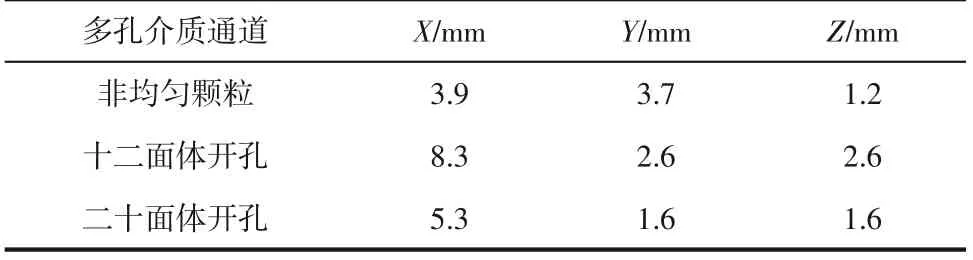
表1 3种多孔介质填充通道的几何尺寸

表2 多孔介质骨架材料的物性参数
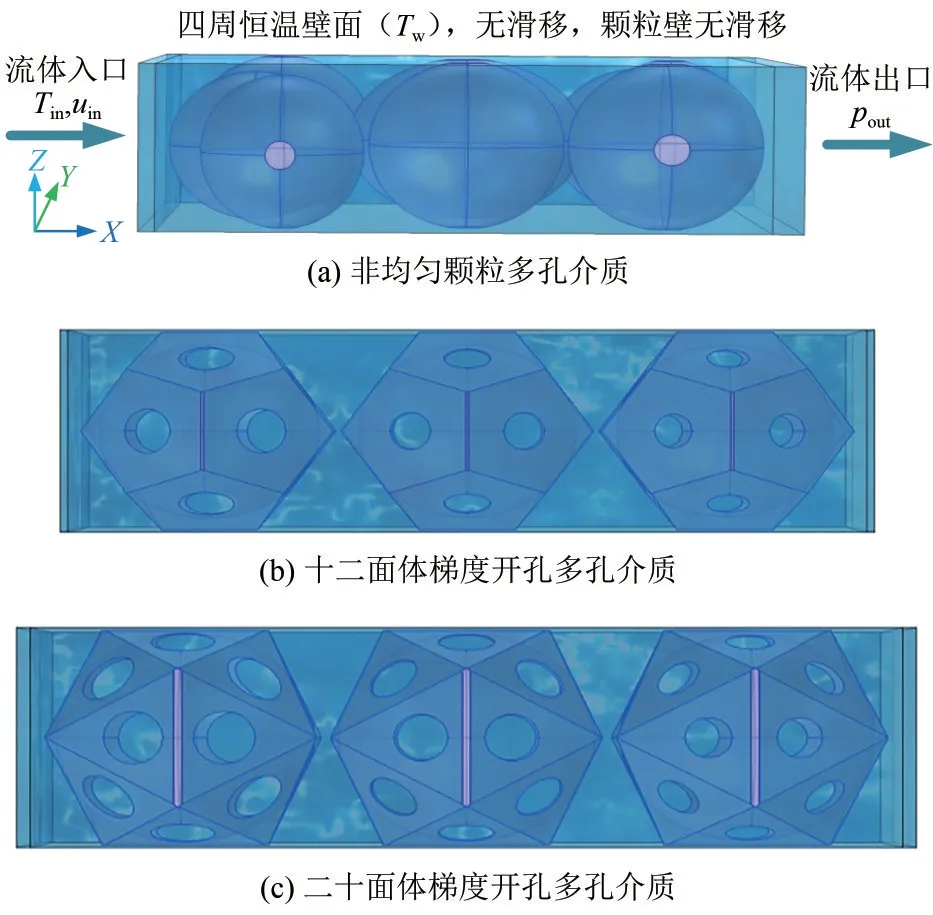
图1 不同多孔介质储层的物理模型
1.2 控制方程和计算方法
首先,基于研究做出以下假设:①流体为不可压缩流体;②储层内部不发生生物化学反应;③固体的热导率为各向同性;④在整个传热过程中不考虑辐射换热。
基于上述假设流体在多孔介质储层内的流动控制方程如式(1)和式(2)所示。
式中,ρf、μ、p分别为流体的密度、动力黏度和压力;u为流体速度矢量;I为单位张量;F为体积力。
固体域和流体域的传热控制方程如式(3)和式(4)所示。
式中,ks、kf分别为固体和流体的热导率;cp,f为流体定压比热容;Q为流体与固体间的耦合换热源。水作为储层内的换热介质,其物性参数可描述为温度的函数[式(5)~式(8)][17]。
研究中使用共轭传热模型对不同多孔介质储层内的对流换热进行直接模拟,非等温流体流动与固体和流体传热相耦合,通过有限元法对控制方程进行离散化处理,并使用向后微分公式(BDF)求解器对时间变量求解,它是一种向后差分的隐式求解算法,根据物理场对计算收敛容差进行优化控制。
1.3 初始条件和边界条件
设置的边界条件和初始条件如下。
(1)储层入口:Tf=Tin,u=uin
鉴于以上的三种原因,我们特制定如下的改进措施,加大畜牧局档案管理工作的力度,把这项工作力争做到实处,取得应有的效果。
(2)储层出口:p=pout
(3)四周壁面:T=Tw,-n·ρfu=0
(4)骨架壁面:-n·ρfu=0
(5)初始状态:u=u0,p=p0,Ts=Tw,Tf=T0
1.4 网格无关性检测和模型验证
采用四面体网格单元划分计算域,在填充结构附近对网格进行了加密,表3给出了非均匀颗粒结构在不同网格数下的流体出口温度,使用Richardson外推法[18]进行了网格独立性验证,R小于1 时,数值结果被认为是收敛的。采用同样的方法对其他两种结构网格进行了检验,最终所使用的网格数见表4。
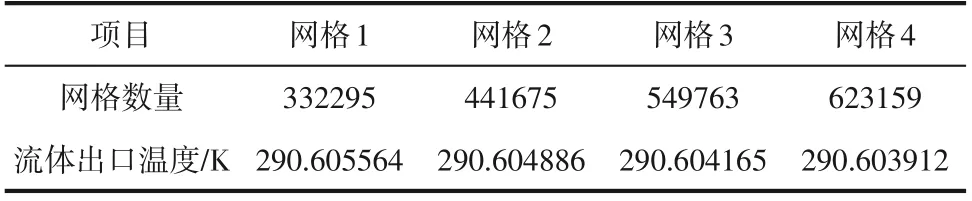
表3 非均匀颗粒多孔介质在不同网格数下的流体出口温度(Re=1, Tw=290.65K)

表4 不同多孔介质模型的网格数
为了验证目前计算模型和方法的可靠性,与Romkes 等[19]所研究的类似问题进行了对比。所采用的物理模型如图2 所示,8 个均匀的球形颗粒有序堆积在矩形通道内,通道高度与颗粒直径之比为1,通道壁面绝热,颗粒壁温度恒定,空气为冷却流体,其进口温度和速度恒定。将模型求解得出的颗粒壁面与流体间的平均努塞尔数与文献中的数值模拟和实验结果进行对比。如图3所示,计算结果与Romkes 等的实验以及模拟结果都具有相同的变化趋势,在低Re(Re<25)下计算结果与Romkes等的结果吻合较好,如Re为10时,与Romkes的计算结果偏差为2.6%。随着Re的增大,惯性力的影响逐渐增强,多孔介质内的流动将由黏性占主导的Darcy流转变为Forhheimer流,本文采用的Darcy模型计算偏差会增大。但本文研究涉及的Re小于10,采用该计算模型和方法进行模拟是可靠的。
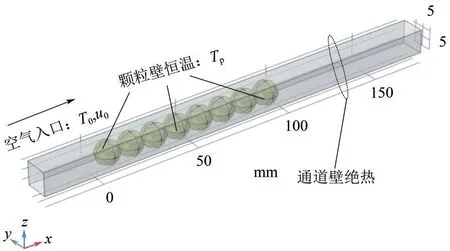
图2 Romkes等所使用的物理模型
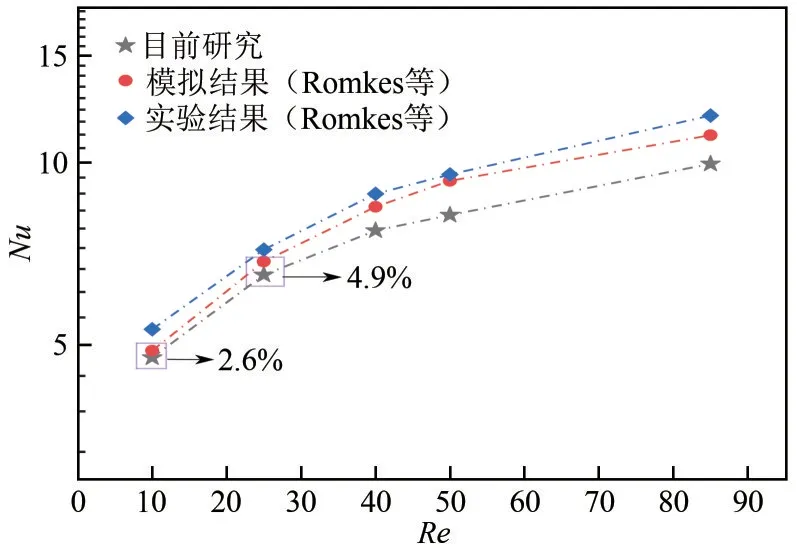
图3 计算结果与Romkes等实验以及模拟结果的对比
2 结果和讨论
2.1 流动和换热关系式
通过对填充单元流动和换热的模拟计算,得到了不同多孔介质结构的单位压降(∆p/∆x)、摩擦系数(f)、骨架壁面与流体间的平均对流传热系数(hsf)、平均努塞尔数(Nusf)和总体换热效率(η),其计算如式(9)~式(17)。
2.2 多孔介质储层内的流动特性
本节主要讨论不同的多孔介质骨架结构储层内的流动特性。非均匀颗粒、十二面体梯度开孔和二十面体梯度开孔多孔介质储层内的截面速度分布以及空间流线分布分别如图4(a)~(c)所示。流体的入口温度为278.15K。从空间流线分布可以看出,在多孔介质通道内,流体在骨架孔隙内的混合和扰动增强,进而影响流体与固体之间的换热和压降。在相同Re和Tw下,模拟结果表明非均匀颗粒通道内的体积平均流速最大,十二面体梯度开孔通道内的体积平均流速最小。非均匀颗粒多孔介质通道内x-y截面速度分布和空间流线分布以及骨架孔隙处的局部放大如图4(a)所示,x-y截面流速波动明显,较大的流速主要集中在孔隙中心区域,由于壁面黏性效应,骨架壁面附近的流动阻力较大,局部流体速度较小,远离壁面后黏性作用减小速度递增;另外,流体在多孔介质通道内绕掠颗粒,掠过前半部时,流动截面缩小,流速增加,压力递降,而在后半部流动截面增加,压力回升,产生了与渗流方向相反的回流;同时从局部孔隙放大图可以发现流体在孔隙区域的混合和扰动较强进一步增大了流速。在图4(b)中,十二面体梯度开孔多孔介质通道内较大的流速主要集中于开孔区域附近而中心区域流速较小,这主要与十二面体开孔结构的开孔位置有关,观察流线分布可以看出流体进入通道后优先选择最近的开孔区域绕流,由于流动截面的减小在开孔位置处的流速急剧增加,当进入骨架中心区域后流动截面增大,流速下降;另一方面由于开孔数较少,从y-z截面的速度和流线分布可以看出,中心区域的混合和扰动较弱。与图4(b)相比,图4(c)中二十面体梯度开孔结构中心区域的速度较大,改变开孔位置角度以及增加开孔数后流体在中心区域的混合和扰动增强,多方向进行绕流,在中心区域产生了回流和漩涡,这有利于强化流体与多孔骨架之间的传热。
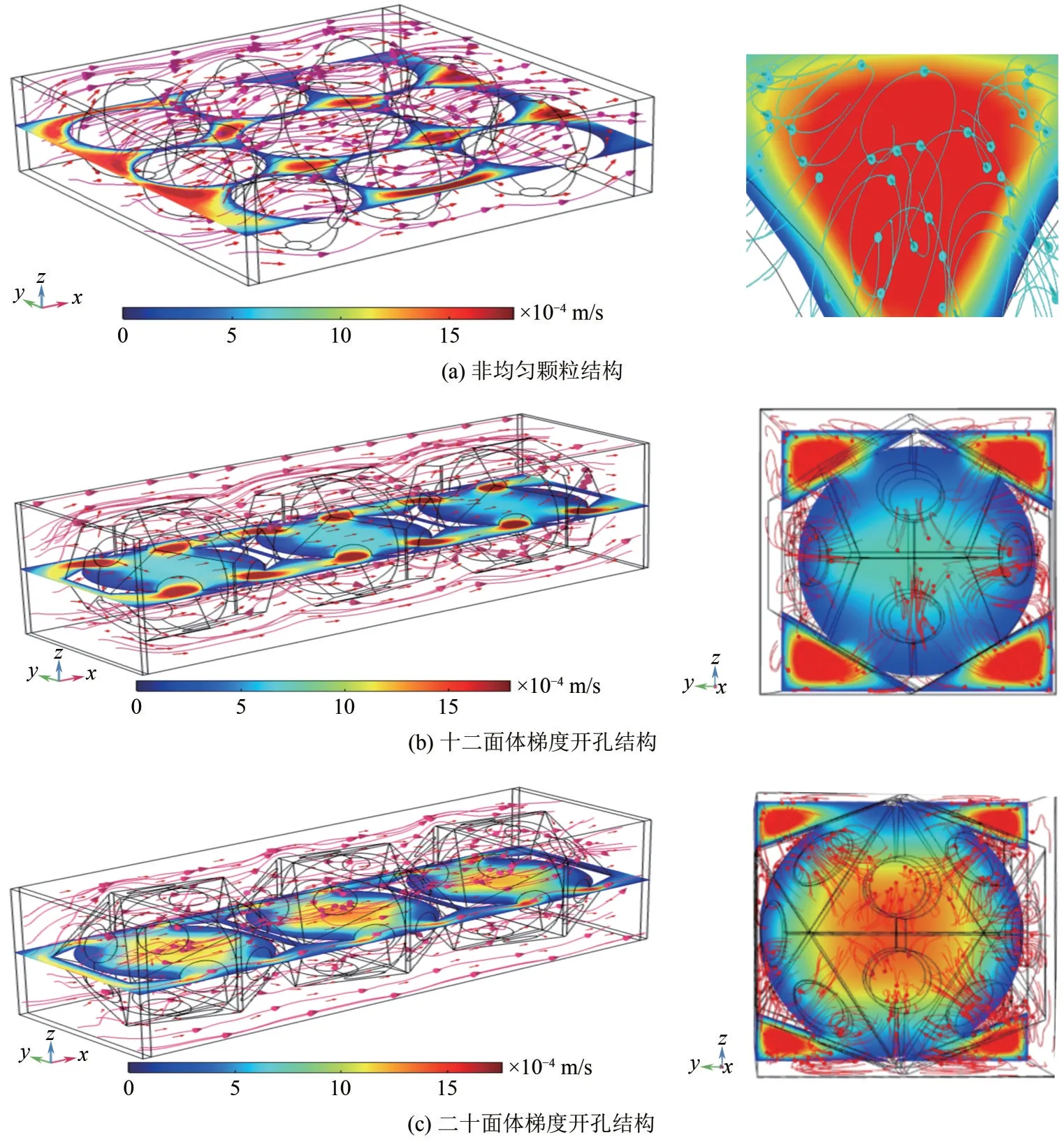
图4 不同多孔介质结构下的截面速度分布和空间流线分布(Re=1, Tw=318.15K)
不同多孔介质结构以及壁面温度Tw下流体单位压降的变化如图5所示,Re范围在0.01~1,Tw为290.65~318.15K。从图中可以看出,非均匀颗粒多孔介质通道内流体的∆p/∆x最大且随着Re的增大增加幅度也最大,而十二面体梯度开孔多孔介质通道内的∆p/∆x最小且变化幅度最小,这与局部流速变化相吻合。Re相同时,十二面体梯度开孔结构空间流线分布相对均匀,因此压降较低,非均匀颗粒结构由于外部绕流弯曲度最大,所以流动阻力更大,压降最高。随着Tw的升高,不同多孔介质结构的∆p/∆x都有所下降,由于低Re下黏性力占主导,温度升高后流体的黏度下降。图6给出了不同多孔介质结构以及壁面温度下摩擦系数的变化。随着Re的增加,f先是急剧减小然后缓慢下降。Tw相同时,非均匀颗粒结构的f最大,十二面体梯度开孔结构的f最小,这与图5 中所示的压降变化相符。随着Tw的增大,f逐渐减小,在模拟的Re范围内二十面体梯度开孔与非均匀颗粒两种多孔介质的f较大且相差较小,而十二面体开孔多孔介质的f则明显较小,这与多孔介质的结构特性有关,流体在非均匀颗粒多孔介质通道内的迂曲度最大而在十二面体开孔结构通道内的迂曲度最小。以上分析能够得出,多孔介质结构对流动特性影响显著,在研究的3种多孔介质结构中,十二面体梯度开孔结构的流动阻力最小。实际应用中选择合适的多孔介质结构可以降低流体的单位压降,从而减小流动阻力和流动功耗。
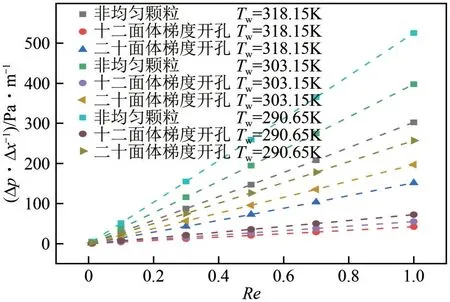
图5 不同结构和壁面温度下单位压降随Re的变化
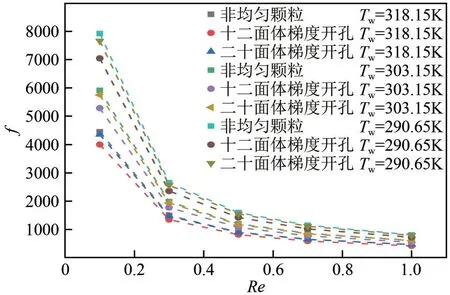
图6 不同结构和壁面温度下摩擦系数随Re的变化
2.3 多孔介质储层内的换热特性
在多孔介质骨架与通道壁面温度高于流体温度时,分析了流体流过多孔结构通道的换热特性。在Re=1、Tw=318.15K 的工况下,当换热达到稳定后,不同多孔介质结构的x-y中心截面和距离入口x=0.55mm处y-z截面的温度分布如图7所示。比较图7(a)~(c)的x-y截面云图可以看出沿着渗流方向不同多孔介质结构整体的温度分布相似,均呈现出壁面附近温度较高而中心区域温度较低的分布。这是因为通道壁面温度恒定,由于多孔介质骨架与通道壁面之间的导热作用,通道壁面附近固体骨架的温度也较高,流体与通道壁面和多孔介质骨架之间的换热较强。而在通道中心区域由于流体与固体骨架之间的换热作用骨架温度降低较快,固体骨架与流体的温度均较低。对比图7(a)~(c)的y-z截面温度云图可以看出,距入口相同距离处二十面体开孔结构和非均匀颗粒结构中心区域的流体温度较高,而十二面体开孔结构中心区域温度则较低,说明十二面体开孔结构流体的换热效果最差。这与之前的流动分析结果相吻合,十二面体梯度开孔结构在中心区域的混合和扰动较弱,流速较小,换热较弱;而其他两种多孔结构通道内流体绕掠骨架过程中在中心区域的混合和扰动较强,因此流速较大,换热更强。
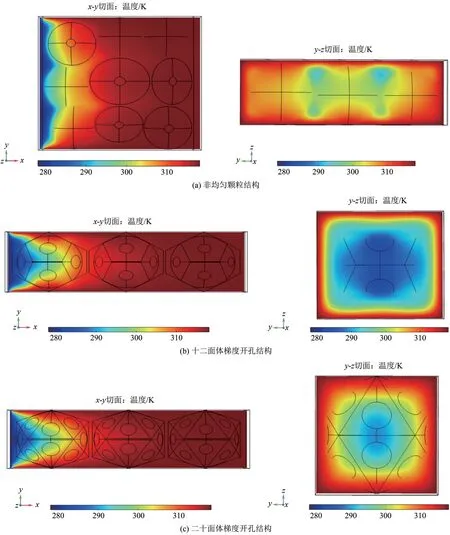
图7 不同多孔介质结构下x-y中心截面和距入口0.55mm处y-z截面的温度分布(Re=1,Tw=318.15K)
不同多孔介质内流体与骨架间的平均对流传热系数的变化如图8所示。可以看出非均匀颗粒的hsf高于其他两种多孔介质,在Re增大时更加明显,十二面体梯度开孔的hsf最小,换热效果最差。Re一定时增大Tw,不同多孔介质的hsf均得到提高,Re越大,升高壁面温度后对流传热系数的增大越明显。这是由于一方面Tw升高增大了流体与壁面间的换热温差,另一方面流体物性随温度发生变化,温度升高后流体的热导率增大,黏度和比热容减小,影响流体与壁面之间的换热。图9给出了不同多孔介质内Nusf的变化,其中非均匀颗粒结构的Nusf值最大,对流传热性能优于另外两种多孔介质。在Re=0.6~0.8之间,十二面体梯度开孔结构和二十面体梯度开孔结构的Nu值存在交叉,在交叉点之前即Re较小时,二十面体开孔结构的换热能力占优,随着Re的增大,二十面体梯度开孔多孔介质的Nusf增加幅度逐渐减缓,而十二面体梯度开孔多孔介质的Nusf则一直保持较高的上升幅度,因此换热性能逐渐优于二十面体梯度开孔结构。当壁面温度变化时,由于温度的改变对流体物性的影响,交叉点也随之发生变化。
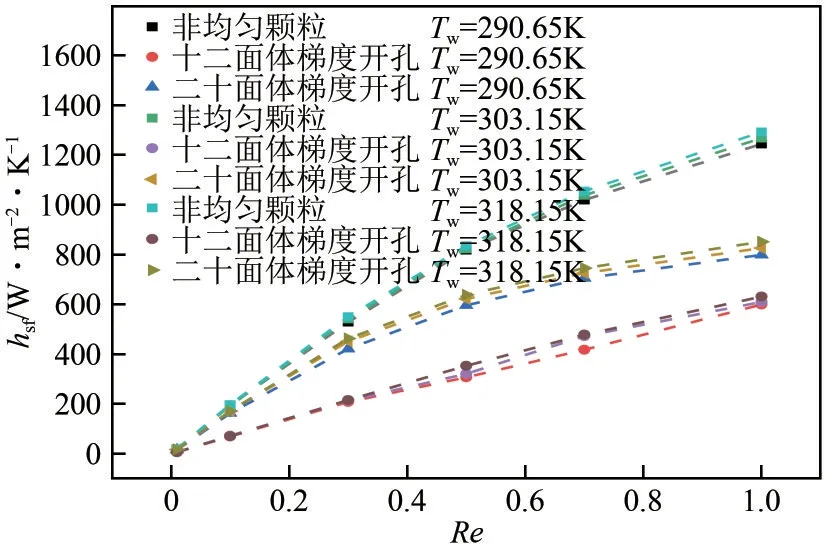
图8 不同多孔介质与壁面温度下hsf随Re的变化
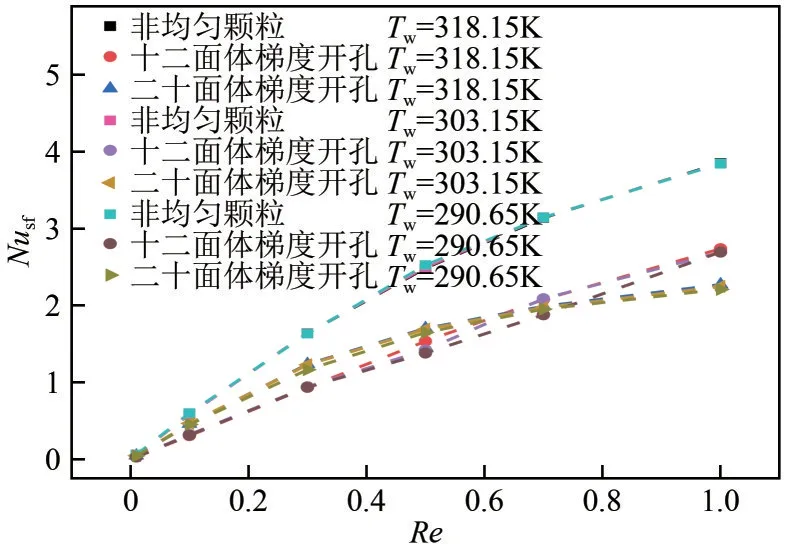
图9 不同多孔介质与壁面温度下Nusf随Re的变化
2.4 多孔介质储层的总换热效率
在多孔介质传热中,增大流体与骨架之间的换热面积(即固体骨架的比表面积),可以提高换热效果,但是流体在多孔介质内部的流动阻力也会增大,造成系统运行过程中循环泵电耗增大。文献中大多未考虑多孔介质内的流动阻力,仅对地下储层的换热性能进行评价[4-6],不能对储能系统进行全面评价。为了综合评价流体在地下储层流动过程中的换热效果和流动阻力,本文使用总换热效率η,即单位压降的换热量来评价储层内的整体换热性能。不同填充结构和壁面温度下总换热效率η的变化如图10 所示,可以看出随着Re的增加不同多孔介质储层的η均略有降低。相同壁面换热条件下,十二面体梯度开孔多孔介质的η远高于其他两种结构,非均匀颗粒与二十面体梯度开孔的η相对较低且比较接近。这表明非均匀颗粒多孔介质和二十面体梯度开孔多孔介质在强化传热的同时流动阻力增加较大。所以在3种多孔介质中,尽管十二面体梯度开孔多孔介质的换热性能低于其他两种结构,但由于摩擦系数和单位压降远低于其他两种结构,综合考虑换热和流动阻力,其总换热效率最大,综合性能最好。当Re一定时,随着Tw的增大,不同多孔介质的η均增大,其中十二面体梯度开孔的增加幅度最大。增大Tw后,一方面冷流体与高温骨架之间的换热温差增大,换热能力增强,另一方面由于流体黏度随温度升高而减小,流动阻力减小,因此不同多孔介质储层的总传热效率随着壁面温度的增大均增大。
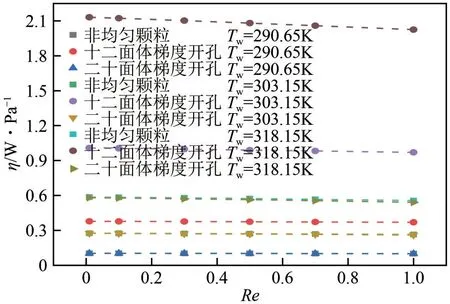
图10 不同多孔介质结构和壁面温度下η随Re的变化
3 结论
对非均匀颗粒、十二面体梯度开孔和二十面体梯度开孔3种多孔介质内的流动和换热特性进行了模拟研究,对比分析了3种结构内流体的单位压降、摩擦系数、对流传热系数、平均努塞尔数及综合换热效率,并探讨了Re以及壁面温度Tw的影响。研究得到了3 种结构填充的多孔介质内的流动特性、传热特性以及总换热效率的大小,在人工构建地下含水储层时,可指导选取合适的填充材料的几何结构。主要结论如下。
(1)在相同的Re和Tw下,3种多孔介质中十二面体梯度开孔的∆p/∆x和f最小,非均匀颗粒的∆p/∆x和f最大。减小Re和增大Tw均可减小单位压降,从而减小流动阻力及循环泵功耗。
(2)在相同的Re和Tw下,3种多孔介质中非均匀颗粒的hsf与Nusf最高,十二面体梯度开孔的hsf最小。二十面体梯度开孔多孔介质与十二面体梯度开孔多孔介质的Nu随Re的变化存在交叉,Re较小时二十面体梯度开孔的Nusf较大,Re较大时十二面体梯度开孔的Nusf较大。交叉点出现在Re为0.6~0.8之间,交叉点的Re会受Tw的影响而变化。
(3)综合考虑压降和换热性能的评价指标总换热效率η,十二面体梯度开孔多孔介质的最高,二十面体梯度开孔与非均匀颗粒的比较接近。随着Re的增大不同结构的η均有所下降,Tw升高后不同结构的η得到明显改善。

