求解一类隐式互补问题的加速模系矩阵分裂迭代方法

黎科良 ,柯艺芬 ,马昌凤

(1.福建师范大学数学与统计学院,福建 福州 350117;2.福建省分析数学及应用重点实验室,福建 福州 350117;3.福建省应用数学中心,福建 福州 350117)

1.引言

近年来,隐式互补问题引起了广泛的关注,其可视为线性互补问题的一种推广.互补问题在经济学和工程中有着广泛的应用,如: 空间价格平衡、对策论模型、接触力学问题、断裂力学问题等[1].本文考虑如下隐式互补问题(ICP): 求Rn,满足:

其中Rn×n是大型稀疏矩阵,Rn是一个给定的实向量,m(z)是一个从Rn到自身的映射.当m(z)0时,隐式互补问题(1.1)退化为线性互补问题(LCP).

目前,已经有许多有效算法被提出用于求解隐式互补问题(1.1),如: 不动点方法[2]、投影法[3]、牛顿方法[4]等.2010年,BAI[5]提出了模系矩阵分裂迭代方法求解线性互补问题,该方法具有形式简单、收敛速度快等优点.随后,HONG和LI[6]首次推广了模系矩阵分裂迭代法和模系矩阵同步多分裂迭代法来求解隐式互补问题(1.1),研究了当系统矩阵A为正定矩阵或H+-矩阵时算法的收敛性质.值得一提的是,模系矩阵分裂方法这一思想已被推广到求解其他互补问题,如: 二阶锥互补问题[7]、旋转锥互补问题[8]、水平线性互补问题[9]、弱线性互补问题[10]和拟互补问题[11]等.

为了解决文[6]对于初始向量的约束问题,ZHENG和Vong[12]在文[6]的基础上建立了一种新的方法,并给出了算法对于任意初始向量都收敛的全局收敛性条件.特别地,当系统矩阵A是正定矩阵或H+-矩阵时,从理论上严格分析了算法的收敛性质.

为进一步加快求解隐式互补问题的收敛速度,并充分利用系统矩阵所包含的信息,本文提出了一类新的基于模系的两步矩阵分裂迭代法(简记为TMMS).进一步,讨论了该方法在一定条件下的收敛性,并分析了该方法在系统矩阵为正定矩阵时的收敛性质.数值实验表明所提出的方法优于原来的模系矩阵分裂迭代方法.

本文分别用∥A∥和∥x∥表示矩阵A的谱范数和向量x的2-范数.用I表示适当维数的单位矩阵.令A=M −N,若矩阵M是非奇异的,则称A=M −N为A的一个分裂.

2.两步模系矩阵分裂迭代法

下面先给出一个重要的引理.

引理2.1[6]假设A=M −N是矩阵A的一个分裂,γ是一个正常数,Ω是一个正对角矩阵.若g:RnRn是可逆映射且g(z):=z −m(z)=(|x|+x),可得

进一步,下面两个结论成立.

(i) 如果(z,w)是问题(1.1)的解,则x=(z −Ω-1w −m(z))满足隐式不动点方程:

(ii) 如果x满足隐式不动点方程(2.1),则(z,w)是问题(1.1)的解,其中

基于引理2.1,文[12]提出了如下模系矩阵分裂迭代法(简记为MMS)用于求解隐式互补问题(1.1).

算法2.1模系矩阵分裂迭代法[12]

步1 给定ε>0,γ>0,x(0)Rn,Ω为正对角矩阵.置k:=0.

步2 通过求解下列线性方程组,计算z(k):

步3 若∥min{Az(k)+q,z(k)−m(z(k))}∥<ε,算法停止;否则,转步4.

步4 通过求解下列线性方程组,计算x(k+1):

置k:=k+1,返回步2.

当A是正定矩阵或H+-矩阵时,文[12]给出了算法2.1的收敛性证明.

为进一步加快算法2.1的收敛速度,基于文[13-17]的研究工作,本文提出一类新的两步模系矩阵分裂迭代方法.

设A=M1−N1=M2−N2为矩阵A的两个分裂,可得如下两步迭代格式:

具体地,基于式(2.5)构造如下两步模系矩阵分裂迭代法(简记为TMMS).

算法2.2两步模系矩阵分裂迭代法

步1 给定ε>0,γ>0,x(0)Rn,Ω为正对角矩阵.置k:=0.

步2 通过求解下列线性方程组,计算z(k):

步3 若∥min{Az(k)+q,z(k)−m(z(k))}∥<ε,算法停止;否则,转步4.

步4 通过求解下列线性方程组,计算x(k+1):

置k:k+1,返回步2.

算法2.2建立了求解隐式互补问题(1.1)的两步模系矩阵分裂迭代法的一般框架.通过选取适当的矩阵分裂和迭代参数,可得一系列的两步模系矩阵分裂迭代法.

当m(z)0时,算法2.2退化为求解线性互补问题的两步模系矩阵分裂迭代法,即

设AD −L −U,这里D,−L,−U分别是矩阵A的对角部分、严格下三角部分和严格上三角部分.考虑如下两个分裂AM1−N1M2−N2,其中

(i) 当α1,β0,称算法2.2为基于两步模系Jacobi迭代方法,记作TMMJ.

(ii) 当αβ1,称算法2.2为基于两步模系Gauss-Seidel迭代方法,记作TMMGS.

(iii) 当αβ,称算法2.2为基于两步模系SOR迭代方法,记作TMMSOR.

3.算法的收敛性

本节将建立系统矩阵A为正定矩阵情形下两步模系矩阵分裂迭代法求解隐式互补问题(1.1)的收敛性分析.

定义3.1称映射m:RnRn是利普希兹连续的,如果对于任意的向量z,Rn,存在一个正常数L>0,有∥m(z)−m(y)∥≤L∥z −y∥.

下面考虑算法2.2的收敛性.假设x∗为式(2.7)的精确解,即

基于式(3.2)建立算法2.2的收敛性定理.

定理3.1假设AM1−N1M2−N2为A的两个分裂,Ω为正对角矩阵,γ为正常数.假设矩阵Ω+M1和Ω+M2都是非奇异的,且函数m: RnRn为利普希兹连续的,即存在正常数L,使得对任意的向量z,Rn,有∥m(z)−m(y)∥≤L∥z −y∥.

记

注意到对于任意的向量y,Rn,有∥|y|−|z|∥≤∥y −z∥.从而

对式(3.3)的第一个等式两边同时取2-范数,可得

同理,对式(3.3)的第二个等式两边同时取2-范数,可得:

从而∥x(k+1)−x∗∥≤ρ2ρ1∥x(k)−x∗∥.当ρρ2ρ1<1时,定理3.1结论成立.

特别地,对于A为正定矩阵,M1,M2Rn×n为对称正定矩阵,ΩωIn,从定理3.1可得如下收敛性结论.

定理3.2假设AM1−N1M2−M2是正定矩阵A的两个分裂,M1,M2Rn×n是对称正定矩阵,ΩωIn(ω>0),γ是一个正常数.用µmax和µmin分别表示M1的最大特征值和最小特征值,λmax和λmin分别表示M2的最大特征值和最小特征值.假设函数m:RnRn为利普希兹连续的且利普希兹常数为L.记

假设迭代参数ω满足下列情况之一:

整理可得,当ω满足定理3.2的四个条件之一,可得s2s1<1.从而

4.数值实验

本节将给出一些数值算例来验证所提出的两步模系矩阵分裂迭代法的有效性.数值实验将所提出的TMMJ、TMMGS和TMMSOR算法与文[12]所提出的MMJ、MMGS和MMSOR算法进行对比,从迭代步数(IT)、所消耗的时间(CPU)和残差范数(RES)三个方面来比较算法的优劣,其中容忍误差ε取值为10-6,残差范数定义为:

这里z(k)是算法第k步的近似解.在实验中,初始向量x(0)的每个分量取值为[−1,1]的随机数,正对角矩阵Ω取为:ΩωDA,ω>0,这里DA为矩阵A的对角部分.实验中的最大迭代步数设为600.所有数值实验均在一台CPU为1.8GHz、内存为8GB的计算机上运行,编程语言为MATLAB R2021a.

例1设s为给定的正整数且ns2.考虑隐式互补问题(1.1),其中Rn×n为如下的块三对角矩阵

这里Stridiag(−1,4+ν,−1)Rs×s且ν>0.向量q(−1,1,−1,1,...,(−1)n-1,(−1)n)TRn.容易验证系统矩阵A是一个对称正定的M-矩阵.函数m(z)分别选取sin(z)和|z|两类非线性函数.

对于例1,考虑取n3600和n4900两种情形进行测试.在数值实验中,参数γ ≡1.5,ν ≡4和ω ≡1.2,在TMMSOR分裂迭代法中,松弛参数α ≡β ≡1.5.表4.1-4.2给出了例1的数值结果.从表4.1-4.2的数值结果可以看出,所有的算法均能快速收敛到隐式互补问题的一个近似解,且随着维数n的增加,TMMS和MMS的迭代步数和CPU会有所增加.在误差方面,所有的算法都能在给定的最大迭代次数内达到终止条件.特别地,从表4.1-4.2的数值结果可以看出,当非线性项的系数增大时,算法往往需要更多的迭代步数才能收敛,如: 当维数相同时,m(z)0.9|z|相比m(z)0.75|z|和m(z)0.5|z|,算法需要更多的迭代步数才能达到终止条件.

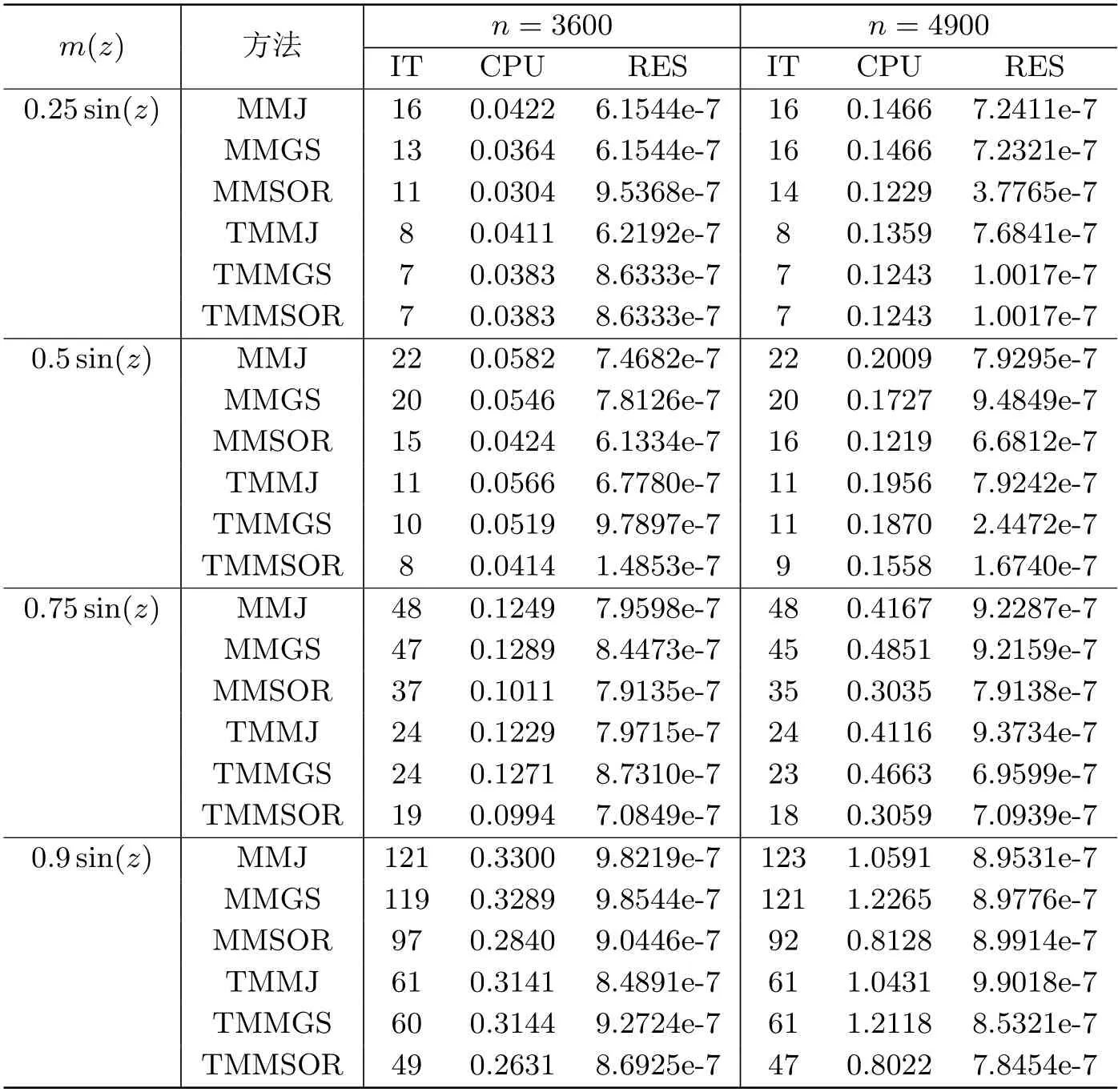
表4.1 例1的数值结果(ν=4)

数值结果表明,TMMJ、TMMGS和TMMSOR的迭代方法要比文[12]的收敛效果更好.因此,本文提出的算法优于文[12]所提出的算法.

5.小结

本文建立了一类新的基于模系的两步矩阵分裂迭代法来求解隐式互补问题.给出了算法收敛的充分条件.数值实验表明,本文提出的方法是有效的,且在迭代步数和CPU时间方面优于传统的方法.然而,算法的收敛速度如何依赖于参数ω仍然是未知的.因此,理论上研究最优参数的选取将是一个值得研究的课题.