在随机启动(p, N)-策略控制下不中断多重休假排队系统的性能分析
袁雨梅,唐应辉,刘雨欣,陈镰元
(四川师范大学数学科学学院,四川 成都 610068)
1.引言
在连续时间和离散时间排队模型的研究中,有大量文献研究了带有服务员休假机制和系统控制策略的排队模型,其中经典的一维控制策略包括:N-策略、T-策略、D-策略等[1-3],典型的服务员休假有单重休假、多重休假和多级适应性休假等[4-5].在此基础上,许多作者做了大量的推广和深入的研究工作[6-15],例如文[6]利用递推法讨论了带反馈和单重休假的Geom/G/1 排队系统.进一步,文[7]考虑了基于多重休假的GI/Geom(a,b)/1/N排队系统.基于实际应用,文[9-10,12-13]研究了带有Min(N,V)-策略的排队系统,Min(N,V)-策略是指每当系统变空时,服务员就去休假或离开系统去做辅助性工作以增加系统的收入.在服务员的假期中,如果到达系统的顾客数达到了N个,服务员马上结束休假并开始为顾客进行服务直到系统再次变空,此时服务员的休假是可以中断的.文[11,14]研究了有Min(N,D)-策略的排队模型,这是将N-策略和D-策略联合起来形成的二维控制策略.类似地,文[15]对带双阀值(m,N)-控制策略的M/G/1可修排队系统进行了研究,并通过数值计算实例讨论了其最优控制策略.
在前面的研究中服务员的休假时间都是可中断的,但是在实际生活中的情况并不完全是这样,如果服务员正在从事的辅助性工作的过程是无法终止的(例如某医生帮其他医生救治危重病人),那么这时候只能等服务员完成辅助性的工作后才能返回系统为顾客进行服务.于是将不中断的休假引入到带有控制策略的排队系统研究中,例如文[16]在双水平控制策略的基础上将延迟不中断单重休假与之结合起来,研究了有双水平(m,N)-控制策略和延迟不中断单重休假的M/G/1排队系统.文[17]提出了(p,N)-策略,即(p,N)-策略就是当系统变空时,服务员就关闭系统,当系统累积的顾客数达到N个时,服务员以概率p(0≤p ≤1)启动服务,以概率(1−p)不启动服务,服务员处于通常的闲期直到系统中的顾客数大于N个时再开始为顾客服务.文[18]利用最大熵法研究了有(p,N)-策略和服务台不可靠的排队系统.最近,在一些具有(p,N)-策略的排队模型研究的基础上[19-21],文[21]讨论了双水平随机(p,N1,N2)-策略的M/G/1排队系统,推广了(p,N)-策略的研究.利用全概率分解技术及更新过程理论得到了系统的瞬时队长分布及其拉普拉斯变换的递推表达式,再利用洛必达法则得到了稳态队长分布及队长的随机分解结果.最后通过数值计算实例探究了稳态队长分布在系统容量设计中的重要作用,并在建立费用结构模型的基础上,通过数值计算实例讨论了最优控制策略(N∗1,N∗2).
基于上述,本文将“随机启动(p,N)-策略”与“不中断多重休假”结合起来,建立了在随机启动(p,N)-策略控制下不中断多重休假的M/G/1排队系统.本文的随机启动(p,N)-策略是指,当服务员休假回来时,如果系统中等待服务的顾客数大于等于N(N ≥1)个,则服务员立即启动服务,若系统中有顾客但顾客数少于N个,则服务员以概率p(0≤p ≤1)启动服务,以概率(1−p)不启动服务,服务员处于通常的闲期直到系统中的顾客数累积到N个时才立即启动服务,如果系统中没有顾客,则服务员就进行另一次不中断的休假.在此排队模型中,既考虑了系统频繁启动而带来的成本增加,也考虑了休假回来时在系统中等待顾客的心态,贴近现实实际,也丰富了现有的排队模型.然后我们将利用全概率分解技术,讨论系统从任意初始状态开始的队长的瞬时概率分布,推导出了队长瞬态分布的拉普拉斯变换的递推表达式.进一步根据其递推表达式,再利用洛必达法则得到队长的稳态分布表达式,同时得到了稳态队长分布的概率母函数、平均队长以及附加队长的显示表达式等排队性能指标.最后通过数值计算实例,讨论了系统空闲率p0和附加平均队长¯Ld关于一些参数的敏感性,以及稳态队长分布的表达式在系统容量设计中的重要作用.
2.问题的描述与一些符号说明
本文提出建立的排队模型如下:
1) 顾客的到达间隔序列{τi,i ≥1}是相互独立、同负指数分布F(t)1−e-λt,t ≥0,λ>0的随机变量,顾客的服务时间序列{χi,i ≥1}独立同一般分布G(t),记平均服务时间为1/µ(0<µ<∞).
2) 服务员的多重休假机制与启动服务的随机(p,N)-策略:每当系统变空时,服务员就去进行一次不中断的休假.当服务员休假回来时,如果系统中等待服务的顾客数大于等于N(N ≥1)个,则服务员立即启动服务直到系统再次变空.若系统中有顾客但顾客数少于N个,则服务员以概率p(0≤p ≤1)启动服务,以概率(1−p)不启动服务,服务员处于通常的闲期直到系统中的顾客数累积到N个时才立即启动服务,如果系统中没有顾客,则服务员就进行另一次不中断的休假,休假时间序列{Vi,i ≥1}独立服从任意分布V(t).
3) 顾客的到达间隔时间τ、顾客的服务时间χ与服务员的休假时间V是彼此独立的.
4) 在t0时刻,如果有顾客则立即开始服务,如果系统是空的,则服务员留在系统中等待顾客的到达并立即服务(这样的假设更符合实际情况,但稳态结果与初始状态假设无关).
3.队长的瞬态分布和稳态分布
表示在服务员忙期b中时刻t的瞬时队长分布,且t0时只有一个顾客,服务员忙期b刚开始,即Q1(0)1,Qj(0)0,j>1.
下面我们使用一种直接的概率分析法来讨论系统队长的瞬态分布,而嵌入马尔科夫链和补充变量分析等传统分析技术是无法直接讨论系统在任意时刻t队长的瞬态分布的.令
再把(3.9)式代入(3.7)式,经整理得(3.1)式,再把(3.1)式代入(3.9)式可得(3.2)式.证毕.
定理3.2对ℜ(s)>0和i ≥1,有
证当j1,2,···,N −1时,“时刻t队长为j”可分为三种情形:
1) 时刻t落在服务员忙期中且系统中顾客数为j;
2) 时刻t落在服务员假期中且系统中顾客数为j;
3) 时刻t落在假期结束后的服务员非忙期中且系统中顾客数为j.
类似定理3.1的分解,可得
对i ≥1,同理可得
(3.14)-(3.15)式的L变换
由(3.16)式和(3.17)式可得关系式
再把(3.18)代入(3.16),经整理得(3.10),再把(3.10)式代入(3.18)式得(3.11)式.
当j ≥N时,类似地,“时刻t队长为j”可分为两种情形:
1) 时刻t落在服务员忙期中且系统中顾客数为j;
2) 时刻t落在服务员假期中且系统中顾客数为j.
由全概率分解技术,可得
对i ≥1,同理可得
(3.19)-(3.20)式的L变换
由(3.21)式和(3.22)式可得关系式
再把(3.23)代入(3.21),经整理得(3.12),再把(3.12)式代入(3.23)式得(3.13)式,证毕.
在上面瞬态分析的基础上,下面我们使用洛必达法则,结合引理3.1很容易得到队长稳态分布的递推表达式,这是嵌入马尔科夫链和补充变量分析等传统分析技术不能得到的(嵌入马尔科夫链和补充变量分析等传统分析技术直接得到的只是稳态分布的概率母函数).
将(3.29)式和(3.30)式代入(3.28)式,整理即可证明,证毕.
定理3.5(稳态队长的随机分解) 本文研究的在随机启动(p,N)-策略控制下不中断多重休假的M/G/1排队系统的稳态队长可以分解成独立的两部分之和:一部分是经典M/G/1排队系统的稳态队长,另一部分是由多重休假与(p,N)-策略机制引起的附加队长Ld,且附加队长Ld有如下离散分布:
证由上面(3.31)式可知本文研究的排队系统的稳态队长可分解成独立的两部分之和,下面证明附加队长Ld有上式的离散分布,令
4.一些特殊情形
推论4.3当p1时,即服务员休假结束时,系统中只要有顾客在等待服务,服务员就立即为顾客服务,则本文研究的模型等价于多重休假的M/G/1排队系统[3,5],在上面所得结果中,令p1,即可得与文[3,5]完全一致的相应结果.
推论4.4当p1,P {V0}1时,即服务员不去进行休假且只要系统中有顾客,服务员就立即为顾客服务,则本文研究的模型等价于无休假的经典M/G/1排队系统[5],在上面所得结果中,令p1,P {V0}1,即可得与文[5]完全一致的相应结果.
推论4.5当N1时,即服务员休假结束时,只要系统中有一个顾客在等待服务,服务员就立即为顾客服务,则本文研究的模型等价于多重休假的M/G/1排队系统[3,5],在上面所得结果中,令N1,即可得与文[3,5]完全一致的相应结果.
推论4.6当p0,P {V0}1时,本文研究的模型等价于N-策略M/G/1排队系统[3],在上面所得结果中,令p0,P {V0}1,即可得与文[3]完全一致的相应结果.
5.系统空闲率p0与附加平均队长d关于系统参数的敏感性分析
在本节中,我们将通过数值计算实例来分析系统空闲率p0与附加平均队长随着p,N和休假时间V的变化情况.
取参数λ0.6,µ1.2,θ2.5,利用Matlab软件编写数值计算程序,图5.1反映了附加平均队长随概率p和控制值N的变化情况,图5.2反映了系统空闲率p0随概率p和控制值N的变化情况.

图5.2 λ=0.6,µ=1.2,θ=2.5时,p0随p和N的变化情况
例5.2当G(t)1−e-µt和休假时间为定长分布P{VT}1时,在ρ<1下,与p0的表达式分别为
取参数λ0.6,µ1.2,p0.6,利用Matlab软件编写数值计算程序,图5.3反映了附加平均队长d随休假时间T和控制值N的变化情况,图5.4反映了系统空闲率p0随休假时间T和控制值N的变化情况.

图5.3 λ=0.6,µ=1.2,p=0.6时,d随T和N的变化情况
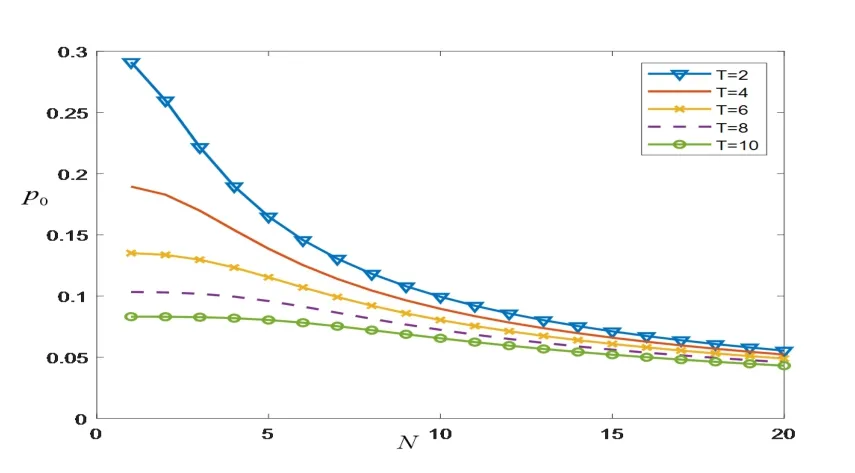
图5.4 λ=0.6,µ=1.2,p=0.6时,p0随T和N的变化情况
由图5.2和图5.4我们可以看出,当休假时间V和概率p确定时,系统的空闲率p0是关于N的递减函数,这是由于当休假时间V和概率p确定时,受N-策略的影响,使得系统中等待服务的顾客数增加,从而系统的空闲率p0呈现减小的变化趋势.根据图5.2可知,当N的取值确定且概率p的取值不断增大时,系统的空闲率p0呈现增大的变化趋势,这是由于当p增大时,进入系统的顾客被及时服务的机率增大,从而使得系统的空闲率p0增大,而当N大于某一值后,p0受N的影响变化得较缓慢,此时主要受p的影响,特别当p1时,系统的空闲率p0是不变的,此时系统的空闲率完全受休假时间V的影响.而从图5.4中我们可知,当N的取值确定且休假时间T的取值不断增大时,系统空闲率p0是逐渐减小的,这是随着休假时间的变长,“服务员忙期”开始时的顾客数不断增加的原因.另外,当N小于某一值时,p0主要受T的影响,且随着休假时间T的增大,休假时间在影响系统空闲率p0时起主导作用的时间越长,p0随N的变化也越来越缓慢,而当N大于某一值时,休假时间T在影响系统空闲率p0时所起的作用越来越小.
6.稳态队长分布{pj}的数值计算与系统容量的优化设计
下面通过对稳态队长分布{pj,j ≥0}的数值计算来说明稳态队长分布{pj,j ≥0}在系统容量的优化设计中的重要作用,从而体现了本文得到稳态队长分布{pj,j ≥0}的表达式(上面定理3.3)的意义.
大家知道,系统容量过大会导致系统的建设成本和管理成本太高,而过低的容量又会导致顾客的丢失,从而引起系统的损失.表6.1给出了在G(t)1−e-µt和V(t)1−e-θt,且令参数λ0.6,µ1.2,θ2.5,p0.6,N10时稳态队长分布{pj,j ≥0}的数值结果.由表6.1可以看出,当j大于某一值后,此时的稳态队长分布pj取值已经接近于零了,所以在系统的容量设计中,我们不需要把系统的容量设计成无穷大.根据表中数据可知:

表6.1 当λ=0.6,µ=1.2,θ=2.5,p=0.6,N=10时,稳态队长分布{pj,j ≥0}的数值结果
由表格结果可知,若按平均队长为标准进行系统容量设计,则到达的顾客因系统容量不够而损失的概率为0.5977,即使按比平均队长大1个单位为参考标准设计,到达的顾客因为系统的容量不够而损失的概率也达到了0.5096.所以我们只依靠平均队长作为系统容量设计的标准是不合理的.
令M是待确定的系统容量,如果要求到达的顾客损失的概率不超过万分之一,即损失的概率不超过0.0001,即
根据表6.1的数据我们可以得到M ≥19,即系统容量取M19即可,由此可见稳态队长分布在系统容量设计上的重要作用,这也体现了本文所获得的稳态队长分布的表达式(定理3.3)有非常重要的应用价值.
7.结语
本文将不中断多重休假机制与随机启动(p,N)-策略结合起来,提出建立了一个新的排队模型,然后使用直接的概率分解分析方法和路径讨论了系统的瞬态队长分布,得到了瞬态队长分布关于时间t的拉普拉斯变换的递推表达式,并利用洛必达法则推得了稳态队长分布的递推表达式,同时得到了一些其他排队指标.最后通过数值计算实例讨论了系统空闲率p0和附加平均队长¯Ld关于系统参数的敏感性,并阐释了稳态队长分布在系统容量设计中的重要价值,弥补了只依靠平均队长进行系统容量设计而带来的不足,使得本文研究结果有更好的应用价值.
- 应用数学的其它文章
- 约束优化问题的单参数填充函数算法
- A New Inertial Tseng’s Extragradient Method for Solving Split Variational Inclusion Problems and Fixed Point Problems
- K-power双线性系统基于Laguerre函数的保结构模型降阶方法
- Lur’e主从系统的二次反馈型脉冲同步控制
- 带有隔离的COVID-19随机SQIR模型研究
- A Hybrid Self-adaptive Conjugate Gradient Projection Method Without Lipschitz Continuity and Its Applications

