K-power双线性系统基于Laguerre函数的保结构模型降阶方法
金辉 ,肖志华 ,祁振中
(1.长江大学信息与数学学院,湖北 荆州 434023;2.西北大学数学学院,陕西 西安 710127)
1.引言
在工程应用领域中,许多物理系统或现象都可以用数学模型来描述,然而大多数的数学模型规模都极其复杂,使得对这些系统的直接仿真模拟和理论分析变得十分困难.因此,有效减小系统规模和缩短计算仿真时间的需求日益上升.模型降阶正是基于此思想,将一个较大规模的复杂系统转化为一个近似的较小系统,同时保留了原始系统的一些重要性能,例如稳定性、结构性和无源性等[1].模型降阶方法已经普遍用于超大规模集成电路模拟、计算电磁学、微机电系统和流体力学等领域[2].
模型降阶自提出以来,已经形成了一系列成熟的降阶理论和方法,例如Krylov子空间方法、平衡截断方法、本征正交分解方法和正交多项式方法等.其中平衡截断是模型降阶最著名的方法之一[3],其基本思想是计算出控制系统的可控Gram矩阵和可观Gram矩阵,进一步构造合适的映射子空间获得降阶模型.该方法可以构造出保持原始系统稳定性的降阶模型,并且给出近似先验误差.然而其需求解两个大规模Lyapunov方程,该过程计算量大且计算时间长,这导致了其应用的局限性.在这种情况下,许多学者作出相应改进,提出了近似平衡截断方法[4].该方法以一种数值高效的方式获得近似平衡系统,被广泛应用于线性系统及非线性系统的模型降阶中.
对于线性系统,相应的模型降阶方法已经日趋完善.而实际的物理系统本质是非线性的,许多物理系统都可以通过双线性系统模型来描述.双线性系统是一类特殊的非线性系统,是连接线性系统和非线性系统之间的桥梁,该系统经常出现在非线性电路、热过程和生态系统等科学领域[5].关于双线性系统的模型降阶,已经发展了多种方法,例如平衡相关方法、Krylov子空间方法和插值法等[6-8].值得注意的是,Shaker和Tahavori在文[9]中定义了双线性系统的交叉Gram矩阵.该交叉Gram矩阵同时反映了系统的可控性和可观性,并且当双线性系统有界输入有界输出(BIBO)稳定时,其为广义Sylvester方程的解.作为双线性系统的一个特殊子类,K-power双线性系统的应用也很广泛,涉及液压驱动建模、多项式系统、非线性系统辨识等领域[10-11].关于K-power双线性系统的模型降阶方法,在文[10]中,Al-Baiyat和Bettayeb首先证明了K-power双线性系统具有块对角可控Gram矩阵和可观Gram矩阵,并提出了一种简化求解Lyapunov方程计算的保结构平衡截断方法.XIE和Syrmos[11]证明了K-power双系统的双线性广义奇异摄动近似(GSPA)可以转化为σ-交互系统的直接截断,基于此,提出了一种基于双线性σ-交互系统分析的方法.WANG和JIANG[12]还成功地将矩匹配方法和最优H2方法应用于K-power双线性系统的模型降阶,进一步得到保持原始系统结构特征的降阶模型.
本文基于Laguerre函数和双线性系统的交叉Gram矩阵,提出了一种K-power双线性系统的保结构模型降阶方法.该方法首先将其等价双线性系统的交叉Gram矩阵用Laguerre函数进行展开,并结合其正交性,进一步给出交叉Gram矩阵的低秩因子,最后通过构造K-power双线性系统各子系统的投影变换得到降阶模型.相比于经典的平衡截断方法,此方法不需要直接求解Sylvester方程来获得交叉Gram矩阵,具有较高的计算效率和灵活度,且具有一定的自适应性.
本文首先介绍Laguerre函数的相关重要性质,接着详细给出保结构的K-power双线性系统降阶过程,并给出了相应的降阶算法.最后,通过数值实验有效验证了算法的有效性.
2.矩阵指数函数的Laguerre函数展开
矩阵指数函数eAt又称状态转移矩阵,在现代控制理论中,可以将其用于状态方程的求解.本节的目标是利用Laguerre函数[13]对矩阵指数函数进行展开.
类似地,对于含有一个稳定矩阵A(若Cn×n的所有特征值严格位于复平面的左半平面,则称A为稳定矩阵) 的矩阵指数函数eAt,可作下列Laguerre展开[16]
其中Laguerre系数矩阵Ak满足
I为单位矩阵.
3.K-power双线性系统的保结构模型降阶算法
考虑如下K-power双线性系统[1,17]:
双线性系统(3.3)的交叉Gram矩阵[9]为
其满足如下广义的Sylvester方程:
i1,2,···,l,j1,2,···,N −1.
其中{α1,α2,···,αN}为CF-ADI参数,且Re(αj)<0.假设所有CF-ADI参数为−α,我们有
因此,除了符号的正负性,低秩因子F与CF-ADI迭代得到的低秩因子Zn相同,即,当所有参数αj与α相同时,上述方法与ADI方法具有等价性。
由式(3.5)得到交叉Gram矩阵Rl的低秩因子,可以将其应用到等价的双线性系统来构造投影变换矩阵,进而生成降阶模型.但该方法没有保留K-power双线性系统自身的结构,而在工程设计和控制应用中,通常要求保留原系统的结构.K-power双线性系统包含k个子系统,且这些子系统依次耦合,其具有保留该系统耦合结构的必要性.为此,通过构造该系统各子系统对应的投影矩阵的思想[19],首先对F和G作如下分块:
可得系统(3.1)的降阶系统如下
上述降阶过程可由如下算法1描述:
算法1K-power双线性系统基于Laguerre函数的保结构模型降阶算法
其中σ(A)为A的特征值.对于更一般的情况,如何选取最优的Laguerre参数α需要进一步研究.数值结果表明,该最优问题对我们算法中参数α的选取具有指导作用.
降阶系统(3.6)可以写为如下等价的双线性系统形式
定理3.1[20]对于双线性系统Σ,如果A是稳定的,并且可控Gram矩阵P和可观Gram矩阵Q均存在,则双线性系统Σ的H2范数表示为
对于精确求解双线性系统可控Gram矩阵P和可观Gram矩阵Q的平衡截断方法[6]和某些H2优化模型降阶方法[17],可以得到误差系统的Hankel范数或H2范数.一般而言,对于近似平衡截断方法,即,通过近似求解或分解系统可控Gram矩阵P和可观Gram矩阵Q,很难得到与精确平衡截断方法类似的误差估计式.尽管如此,值得注意的是,XIANG在文[21]中证明了矩阵指数函数正交多项式近似的指数收敛性,受此启发,我们可以将该结论推广应用到(双)线性系统Gram矩阵的低秩分解的收敛性分析,并由此估计降阶系统与原系统的误差,该问题有待进一步的研究.
4.数值实验
下面通过一个数值算例来验证上述保结构模型降阶算法的有效性.该数值实验在Intel(R)Core (TM) i5-10210U CPU (1.60 GHZ) PC上进行,内存为16.00GB.同时,选用ode15s函数在MATLAB R2018b中求解系统.
考虑由两个子系统组成的单输入单输出(SISO)K-power双线性系统[12,17,19],并选取每个子系统的阶数均为3000.该系统的系数矩阵如下:
其中B1,R3000.通过本文给出的算法1(Algorithm 1)对该系统进行降阶,该系统优化问题(3.7)的解为α ≈10.数值结果表明,该α值是有效的.取Laguerre函数展开项数N4,误差限tol10-10,由此自适应得到的两个降阶子系统的阶数均为4.同时,分别以文[22]中的Krylov子空间方法(Krylov),文[19]中的Laguerre正交多项式方法(Laguerre)和文[10]中的平衡截断方法(BT)对该系统进行降阶.在Krylov子空间方法中,取q19匹配该系统第一个子系统的前9阶矩,同时选取p22,q24匹配第二个子系统的前4阶矩[19],由此得到的两个降阶子系统的阶数为9和8.由Laguerre多项式方法和BT方法分别得到的两个降阶子系统的阶数也为9和8.
表1分别给出了该系统的输入变量u1(t)10sin(10t+5)和u2(t)sin(4t)e-0.2t时各模型降阶方法的CPU运行时间(包括降阶的时间和模拟降阶系统的时间)、最大相对误差∥y(t)−yr(t)∥2/∥y(t)∥2和加速比,其中yr(t)为降阶系统的输出响应.
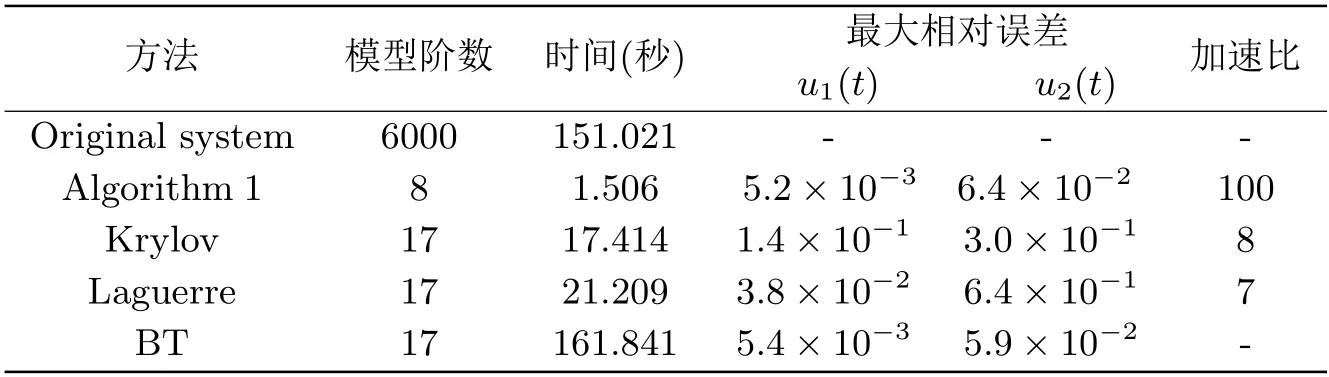
表1 各模型降阶方法的CPU运行时间、最大相对误差和加速比
图1和图2分别给出了输入变量为u1(t)时各降阶系统和原始系统的瞬态响应及其对应的相对误差.

图1 输入为u1时各降阶系统的瞬态响应

图2 输入为u1(t)时瞬态响应的相对误差
图3和图4分别给出了输入变量为u2(t)时各降阶系统和原始系统的瞬态响应及其对应的相对误差.

图4 输入为u2(t)时瞬态响应的相对误差
从模拟结果可以看出,对于该SISO K-power双线性系统模型,由算法1得到的降阶系统对原始系统有很好地瞬态响应近似效果.在相同的近似精度下,算法1构造的降阶系统比BT方法构造的降阶系统的阶数小.算法1构造的降阶系统比Krylov子空间方法和Laguerre多项式方法构造的降阶系统有略好的近似精度,并且算法1得到的降阶系统的阶数小于这两种方法(Krylov,Laguerre)得到的降阶系统的阶数.此外,算法1构造和模拟降阶系统的时间少于其他三种方法(Krylov,Laguerre,BT)所用的时间.这些结果表明,本文提出的算法对于该K-power双线性系统是有效的.
5.结论
本文提出了一种K-power双线性系统基于Laguerre函数的保结构模型降阶方法.该方法首先将K-power双线性系统转化为等价的双线性系统,再结合Laguerre函数的正交性,将矩阵指数函数通过Laguerre函数展开,然后计算出双线性系统交叉Gram矩阵的低秩分解因子,从而构造K-power双线性系统各子系统相应的投影变换,最后得到保结构的降阶模型.通过所提算法得到的降阶系统能很好地近似原始系统的瞬态相应,并且该方法计算高效,具有一定的自适应性.最后,数值实验有效验证了该算法的有效性.

