Lur’e主从系统的二次反馈型脉冲同步控制
王万林,黄振坤,赵玲
(集美大学理学院,福建 厦门 361021)
1.引言
混沌系统是一类非常重要的系统,近年来时滞反馈控制[1]、滑模控制[2-3]、脉冲控制[4]等多种控制方法应用于混沌系统的同步控制,特别是脉冲控制在耦合混沌系统中应用引起了人们的广泛关注[5-8],并在通信保密应用中取得了丰富的成果[9-12].
对于脉冲控制在耦合混沌系统同步问题上的研究,大部分工作都是通过线性输出反馈脉冲来进行的,比如文[13-14]对Lur’e主从系统采用了线性静态测量反馈脉冲控制,得到了一系列使得Lur’e主从系统达到同步的稳定性结果.然而带有二次输出反馈的脉冲控制作用在Lur’e混沌主从系统上甚至其它耦合混沌系统上都尚无相关结果.由于其脉冲控制器上带有二次输出反馈项,处理起来十分麻烦且无现有方法可直接套用.Amato等人在文[15-16]中利用多面体凸组合方法研究非线性二次系统这个工作非常具有启发性,此方法加以运用可以解决脉冲控制器上二次输出反馈项所带来的困难.
基于以上观点与启发,本文研究了带有二次输出反馈的脉冲控制在Lur’e混沌主从系统上的同步问题.利用了多面体凸组合与线性矩阵不等式(LMI)[17]并结合Lyapunov稳定性理论,得到主从系统同步的两个新准则.最后针对蔡氏电路与二维Lur’e型动态网络系统进行数值模拟.
2.主从Lur’e系统模型与预备工作
考虑以下带有二次反馈型脉冲的主从Lur’e系统
引理2.1[15]若存在一正定矩阵P和c>0,ρ>1,使得下面不等式成立
那么P ⊂Ω ⊂Pρ,其中Ω为椭球体Rn:eTPe ≤c}.
由多面体P的凸性可得
引理2.2若存在一个正实数µ,使得
则对于任意的,有
3.主要定理
证考虑Lyapunov函数V(e(t))eT(t)Pe(t)和椭球体ΩRn:eTPe ≤c}.根据引理2.1,由(3.1)式和(3.2)式可得
从而在(t0,t1]上,可知
由误差系统(2.4)可得
从而误差系统(2.4)渐近稳定,即主系统M与从系统S达到同步.
定理3.2给定Pconv{e(1),e(2),···,e(p)}Rn:e ≤1,k1,2,···,q}.假设存在一正定矩阵Rn×n,矩阵Rn×l,HiRn×n(i1,2,···,n),α>0,c>0,ρ>1,使得下面不等式成立
证考虑Lyapunov函数V(e(t))eT(t)Pe(t)和椭球体ΩRn:eTPe ≤c}.根据引理2.1,由(3.7)式和(3.8)式可得
因此当任意初始状态e(t0)时,误差系统(2.4)渐近稳定.由于P ⊂Ω,从而当任意初始状态e(t0)也可使得误差系统(2.4)渐近稳定,即主系统M与从系统S达到同步.
注3.1定理3.2条件下,多面体P是该系统一吸引域估计.
注3.2定理3.1与定理3.2的区别在于: 1)定理3.2中的状态矩阵A必须要求为Hurwitz矩阵,定理3.1中的A并无要求;2)定理3.1是在给定初值状态e(t0)下,其对合适的多面体P条件更苛刻,并且初值状态e(t0)不一定在符合条件的多面体P上;3)定理3.1与定理3.2中的∆T∗含义不同.综上可知定理3.1与定理3.2是相互独立的.
4.数值模拟
例1考虑蔡氏电路主从系统,主系统M如下
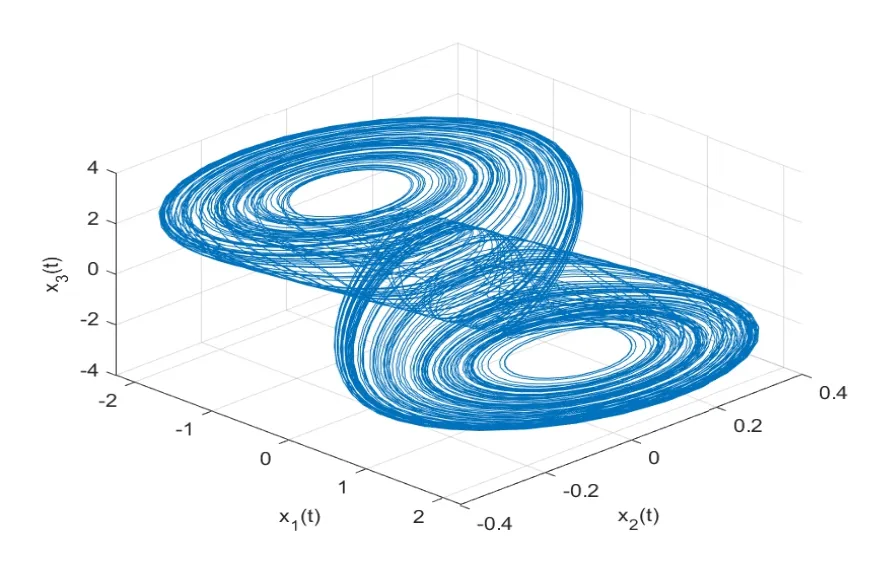
图4.1 主系统M状态图
假设脉冲步长一致,即∆T∆T∗.图4.2为主从系统的状态分量图,图4.3为相应的误差系统状态分量图,很明显可看出主系统M与从系统S产生同步现象.

图4.2 主从系统状态分量x(t),z(t)

图4.3 误差系统状态分量e1(t),e2(t),e3(t)
例2考虑二维Lur’e型动态网络主从系统,主系统M参数选取如下
选取满足定理3.2条件(3.10)中的脉冲增益矩阵K,Hi,i1,2与∆T∗,如下
取一组误差系统初始状态ei(0)(i0,1,2,3),在脉冲步长一致即∆T∆T∗下进行数值模拟,其中
图4.4为相应的误差系统状态分量图,很明显只要误差系统初始状态在多面体P所包含的范围内,主系统M与从系统S产生同步现象.

图4.4 误差系统状态分量ei(t),i=0,1,2,3
5.总结
本文研究了二次输出反馈脉冲控制下Lur’e混沌主从系统的同步问题.基于Lyapunov稳定性理论,结合多面体凸组合与线性矩阵不等式(LMI)方法得到了在二次输出反馈脉冲控制下Lur’e混沌主从系统同步的充分条件.最后数值模拟证实了结果的可行性与有效性.
- 应用数学的其它文章
- K-power双线性系统基于Laguerre函数的保结构模型降阶方法
- Iterative Regularization Method for the Cauchy Problem of Time-Fractional Diffusion Equation
- A Hybrid Self-adaptive Conjugate Gradient Projection Method Without Lipschitz Continuity and Its Applications
- 约束优化问题的单参数填充函数算法
- 带有隔离的COVID-19随机SQIR模型研究
- A New Inertial Tseng’s Extragradient Method for Solving Split Variational Inclusion Problems and Fixed Point Problems

