立足整体建构 凸显数学本质

王蜜　卜骥

［摘 要］数学概念是数学知识的基础。概念教学前，教师不仅要围绕旧知建构概念，还要顺应学情教学。以“小数的意义”教学为例，利用概念本质设计学案让学生练习，让学生在已有知识经验上自主探索，弄清知识之间的联系，慢慢接近概念本质。

［关键词］整体建构；概念教学；小数的意义

［中圖分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）20-0075-03

数学教师要上好数学课，就要“吃透”教材，用“高位”的视角理解教材，知道所教知识的“前情”和“后续”，具有整体眼光、逻辑体系和结构思维，才能了解所教知识的“数学本质”。小学生正处于认知结构发展的初期，需要直观显性的学习内容来增加学生的感性认识。因此，教师要在整体把握教材的基础上巧设学习情境和问题，让学生有更多的机会去经历和感受，着力体现知识的关联性，使学生在充分的探究活动中感悟概念本质，主动获取数学知识。下面以苏教版教材五年级上册“小数的意义”一课的教学为例，结合课堂教学谈一谈笔者的思考和主张。

一、溯源迁移——基于元认知设计概念生长基点

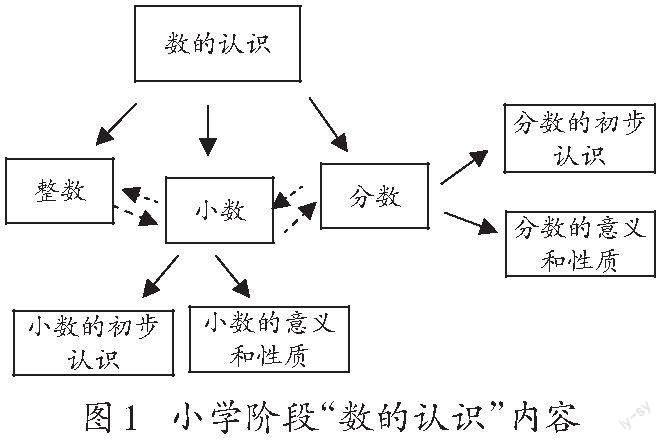
在设计这节课前，笔者将小学阶段“数的认识”内容进行了整理（如图1）。学生在前期的学习中已经理解了整数、分数的意义，初步认识了小数，在生活中也经常用小数来表示一些数，但对小数的意义还没有深刻的理解，要让学生深刻理解小数的价值及意义，概念的建构过程尤为重要。教师需要借助学生已有的知识经验，紧抓小数与整数、分数之间的关系，从数的本源性出发，让学生在学习过程中感悟数的统一性。显然，将小数置于生活化的情境中有助于激发学生探究的兴趣。笔者以学生身边的跳高比赛创设情境。

【教学片段1】巧设情境，激发兴趣

师：同学们喜欢运动吗？喜欢什么项目？（出示跳高图片）这是跳高比赛，跳得越高说明成绩越好。我们来看看某次比赛的成绩。

师（出示比赛第一名和第三名的跳高成绩）：认识这两个数吗？这是我们三年级学习的小数，读一读。

生1：一点四，一点三。

师：李珊是第二名，猜一猜，她的成绩是多少？

（学生猜1.35米、1.36米等）

师（出示李珊成绩：1.38米）：这个小数和之前的两个小数有什么不同？

生2：之前的两个小数的小数点后面有一个数字，这个小数的小数点后面有两个数字。

师：像这样，小数部分有两位的小数叫两位小数，你会读这个两位小数吗？一起读一读。

生（齐）：一点三八。

师：是的，整数部分按照整数的读法，小数部分要一位一位地读出来。小数部分有一位的小数叫什么？

生3：一位小数。

师：既然有一位小数、两位小数，还会有什么？

生4：三位小数、四位小数……

师（出示1.030）：你会读这个小数吗？

……

师：所有的小数都是整数部分按整数的读法，小数部分要一位一位地读。会读小数了，那它表示什么意义呢？我们今天这节课就来研究小数的意义。

从现实情境引入概念有两个目的。第一是将数学问题置于生活情境中，让学生在熟悉的情境中产生探究小数意义的需求。第二是基于这个情境的特殊性让学生感受到小数产生的必要性。因为用整数来表示生活里的一些数量时，往往不能满足现实需求，所以产生了小数，而当一位小数也不足以解决问题时，便要用两位小数。情境中，第二名的成绩介于1.3米和1.4米之间，再根据跳高测量数据一般可能会是一个两位小数的现实性，这样从实际生活入手，有助于学生发现问题，激发学生探索动力。

二、顺学而教——设计学案引导学生触摸概念表象

小学教材的编排有着循序渐进、由易到难的特点。从数的组成来看，小数和整数一样，都是基于计数单位建构的，是十进制的反向延伸。因此教师在建构小数的意义概念时，应抓住它和整数、分数的关系，基于学生已有的知识经验，让学生在“数学化”的活动中建构概念。

【教学片段2】类比迁移，感知本质

师：以前学习了1米、10米和100米之间的关系，那你知道1米和1分米有什么关系吗？可以借助米尺和同学交流。请拿出练习纸，根据学案一的要求自主探索。

学案一：

（1）分一分。拿出米尺，试着将1米平均分成10份，找到1分米。

（2）想一想。1米和1分米有什么关系？你是怎么想的？

（3）说一说。和同学说一说你的想法。

生1：1米里有10个1分米，也就是把10个1分米加在一起，满十进1，进1后是1米。0.1米的“0”在个位上，表示 0米，“1”在比个位低的那一位上，为了区分，用小数点隔开，因此1分米就是0.1米。

师：你联想到了学过的十进制计数法的进位原理，找到了一个新的数位。

师：确实如大家所说，1米=10分米，把 1米平均

生2：3分米是0.3米，8分米是0.8米，道理是一样的。

师：请根据学案二的要求自主探究。

学案二：

（1）你还想将1米平均分成多少份？

（2）1米和1厘米、1毫米有什么关系？

（3）12厘米是多少米？

生3：将1米平均分成100份，此时已经不满0.1米了，所以“1”要再往下写一个数位，每一份就是0.01米，也就是1厘米。

师：刚才我们把1米平均分成了10份、100份，还能再分吗？

生4：可以，把1米平均分成1000份。

……

本课的教学重点是让学生理解小数的意义。引出新知之前，笔者首先利用学案指导学生自主探究1米和1分米的关系。通过思考与交流，学生初步感悟了十分之几的分数与一位小数之间的联系；接着让学生探讨1米与1厘米、1米与1毫米关系，学生通过将旧知类比迁移，主动思考、合作交流，开始研究性学习：将1米不断地细分，依次得到了两位小数、三位小数。在这过程中，学生能深刻体会到小数表示数量的合理性，也不难发现小数和整数一样，都有着“十进制”关系，从整体上感知用小数表示数与用整数、分数表示数方法上的一致性。

三、聚焦本质——在抽象比较中深化概念建构

在苏教版教材体系中，小数的认识在分数的认识之后，因此学习此课前，学生对于分数的意义已经有所了解。对此，教学小数的意义本质时，可以让分数作为学生理解小数意义的桥梁。

【教学片段3】抽象概括，触及本质

师（出示不带单位的分数和小数）：比较这些分数与小数，你有什么发现？

生1：有的分母是10，有的分母是100、1000。小数也是，有的是一位小数，有的是两位小数，还有的是三位小数。

师：这些分数和小数之间有什么联系吗？

生2：分母是10的分数，可以写成一位小数；分母是100的分数，可以写成两位小数；分母是1000的分数，可以写成三位小数。

师：说得很好，这些分数都可以写成小数。那一位小数表示什么？

生3：表示十分之几。

师：两位小数表示百分之几，三位小数表示千分之几，四位小数、五位小数呢？

……

从具体到抽象，是通向数学本质的必经之路。从情境中得到的一个个具有实际意义的分数和小数，分离它们量的属性，它们就成了一个个的数。学生先在观察、比较、发现的过程中，发现这些分数都是十分之几、百分之几、千分之几，而这些小数都是一位小数、两位小数、三位小数；再通过比较一位小数和十分之几的分数的关系，就能归纳出一位小数的意义。学生在概括中逐步剔除了小数的非本质属性，感受到其“十进制数”的本质，在此基础上，继续迁移、类比发现两位、三位小数表示的是百分之几、千分之几，甚至四位、五位小数……表示的是万分之几、十万分之几……顺利地从直观思维过渡到抽象思维。

四、练习固学——再度利用研探内化概念本质

建构数学模型是学习数学的重要方法，更是一种思想。而多式、变化、有趣的练习形式，既能激活学生所学知识，又能助力学生建构基本的数学模型。

【教学片段4】变式练习，回归本质

师（出示数轴）：如果把数轴上“0～1”这一段平均分成10份，每一份是多少？

生1：0.1。

师：你能在数轴上找到零点几的小数吗？想一想，如果把1～2这一段也平均分成10份，在数轴上又可以找到几点几的小数？

生2：1.1～1.9。

师：看来，一点几的小数都在1～2之间。你们找到的怎么都是一位小数？

生3：因为都是把“1”平均分成了10份。

师：只要把“1”平均分成10份，其中的几份表示十分之几，都可以写成一位小数。

师：如果把0～0.1这一段继续分成10份，每一份又是多少？为什么？

生4：0.01，相当于把“1”平均分成100份。

师：只要把“1”平均分成100份，其中的几份表示百分之几，都可以写成两位小数。

师：想一想，如果把0～0.01这一段继续分成10份，每一份又是多少？

生5：0.001。

师：把“1”平均分成1000份，其中的几份表示千分之几，都可以写成三位小数。

师（出示3个小数：0.9、0.09、0.009）：读一读这3个小数，并在数轴上找到它们对应的位置。它们分别表示几分之几呢？为什么都有“9”，但表示的分数和小数都不同？

生6：分数和小数的意义不同。

师：是的，将“1”平均分的份数不同，表示的小数的意义是不同的。

在学生不断感受细分数轴的过程中，数轴充分发挥“模型图”的作用，帮助学生建立数学模型，使学生看到0.1、0.01、0.001马上能想到其对应的模型图。

五、顺逆互动——通过逆向思维助力学生建构

针对所学知识进行归纳和反思，适时“回头望”，多逆向思考，多反思学习过程，是提升学习品质的一种好办法。在课后总结回顾时，教师可以先从“1”出发，通过均分产生的0.1、0.01、0.001等，帮助学生建立小数部分相应的数概念体系；然后从“0.001”出发，10 个0.001是0.01，10个0.01是0.1，10个0.1是1，10个1是 10，10 个 10 是 100……学生进一步感知“不管是整数部分，还是小数部分，每相邻两个计数单位之间的进率都是十”，从整数数系扩充至有理数数系，为后续进一步探究小数积累认知经验。

概念的学习，其最终目的不是为了记住定义，而是要理解概念的本质。不同的认知过程会形成不同的理解水平，若是单纯教学定义，其认知过程主要是模仿、记忆、强化，只能达成“工具性理解”；若突出数学知识之间的本质联系，其认知过程则重在经历、感知、体验，就会形成“关系性理解”。小数产生于实际生产和生活的度量，当量不足或有盈余时，用整数就无法表示了，原来的整数模型就成了束缚思维的“牢笼”，新方案应需而生，因此衍生出了小数。对此，教师要引导学生在认识、理解小数的意义后，把获得的经验、知识、方法应用于本质相同的數学问题中，这样便可以简化思考过程，提高解决问题的效率，提升思维的深刻性、敏捷性。

［ 参 考 文 献 ］

[1] 梅娅.整体意义关联的教学理解与设计：以“小数的意义”的教学为例[J].教学月刊小学版（数学），2022（6）：43-47.

[2] 张优幼.指向认知结构生长的大单元教学[J].教学与管理，2019（26）：31-33.

[3] 万兆荣.结构关联 意义融通：“小数的意义”教学实践与反思[J].小学数学教育，2020（18）：48-50.