一道抛物线检测题的解法与推广探究

湖南省长沙市南雅中学 (410027) 朱 彬

1 试题呈现

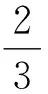
2 试题解答

首先来看第(1)小题的解法.

分析：求曲线标准方程的基本方法是待定系数法,依据l1的斜率设出l1的点斜式方程,与E的方程联立,消去x后得到关于y的一元二次方程,利用弦长公式得到关于参数p的等式,求解得到p的值,从而得到E的标准方程.

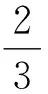
本小题考查待定系数法求抛物线的标准方程和直线与抛物线的位置关系,熟练运用弦长公式是求解的关键.下面重点来研究第(2)小题的解法.

分析：该小题是圆锥曲线的重点题型——定线问题.定线问题是指无论动点如何变化,始终在某条定直线上,问题的本质就是求动点的轨迹(方程).

因为点(-2,0)在抛物线E的对称轴上,所以由抛物线的对称性可知,直线AD与直线BC的交点G必定在垂直与x轴的直线上,因此要证明点G必在定直线上,只要证明点G的横坐标为定值.这样,分别设出A、B、C、D的坐标,表示直线AD与BC的方程后联立,得到用A、B、C、D的坐标表示的点G的横坐标,而整体消去与A、B、C、D坐标有关的部分成为解题的关键.因此,需要首先从直线AB和直线CD的方程着手寻找联系.

思路1 先根据A、B在E上,设出两点的坐标,利用点差法求得斜率式子,表示出直线AB的方程后,将点(-2,0)代入,从而得到A、B两点纵坐标关系;同理得到C、D两点纵坐标关系,进而利用这些关系证得点G的横坐标为定值.这一思路的程序是:设点——表示直线方程——代点(-2,0)——纵坐标关系——结论证明.

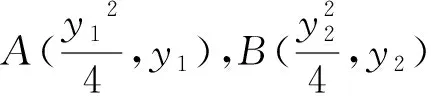
思路2 根据直线AB过点(-2,0),设出点斜式方程,与抛物线方程联立,消元转化,设出点A、B两点纵坐标,由韦达定理得到纵坐标关系,利用点差法求得斜率式子,表示出直线AB的方程后,将点(-2,0)代入,从而得到A、B两点纵坐标关系;同理得到C、D两点纵坐标关系,进而利用这些关系证得点G的横坐标为定值. 这一思路的程序是:设直线点斜式方程——联立方程组——利用韦达定理——纵坐标关系——结论证明.

解法2:因为直线AB过点(-2,0),所以设AB的方程为y=k1(x+2),联立方程组

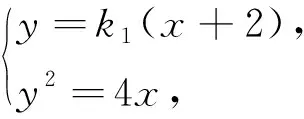
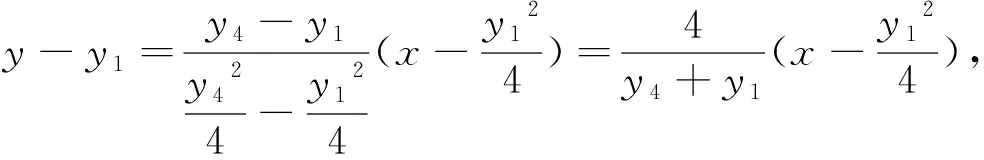
以下同解法1.

思路3 根据直线AB过点(-2,0),设出横斜截式方程,后面的过程同思路2.

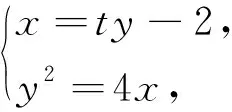
以下同解法1.

点评：解法1是先设点,得到直线方程后将点(-2,0)代入,而解法2和解法3则是直接利用点(-2,0)设出直线的方程,不同之处在于解法2设出直线的点斜式方程,而解法3是设出直线的横截距式方程.设而不求和整体思想则是解决该小题的主要方法和手段.

3 试题变式

探究1 试题中的抛物线E:y2=4x开口向右,点(-2,0)是对称轴上位于y轴左侧的一个已知点,那么,对应于抛物线E另外三种开口方向和已知点的相应位置,是否也有类同于第(2)小题的结论呢?于是有以下三个变式题.

变式1 已知抛物线E:y2=-4x,过点(2,0)的两条直线l2,l2分别交E于A、B两点和C、D两点.设G为直线AD与BC的交点,则点G必在定直线上. (答:定直线为x=-2)

变式2已知抛物线E:x2=4y,过点(0,-2)的两条直线l1,l2分别交E于A、B两点和C、D两点.设G为直线AD与BC的交点,则点G必在定直线上. (答:定直线为y=2)

变式3 已知抛物线E:y2=-4y,过点(0,2)的两条直线l1,l2分别交E于A、B两点和C、D两点.设G为直线AD与BC的交点,则点G必在定直线上. (答:定直线为y=-2)

4 结论推广

探究2 我们根据试题中抛物线方程x的的系数和已知点横坐标的关系,能否将试题结论推广为一般情形?于是有了下面的结论1.

结论1 已知抛物线E:y2=2px(p>0),过点(-p,0)的两条直线l1,l2分别交E于A、B两点和C、D两点.设G为直线AD与BC的交点,则点G必在定直线x=p上.

结论1的证明可按试题的解法过程来完成,这里从略;若变换抛物线的开口方向和已知点的坐标,可得到另外三个类同结论,这里也从略.

探究3 若将结论1中抛物线E的方程不变,将点(-p,0)变为更一般情形,能否得到类同的结论?于是有下面的结论2.

结论2已知抛物线E:y2=2px(p>0),过点(-m,0)(m>0)的两条直线l1,l2分别交E于A、B两点和C、D两点.设G为直线AD与BC的交点,则点G必在定直线x=m上.

若变换抛物线的开口方向和已知点的坐标,可得到另外类同的三个结论,这里从略.