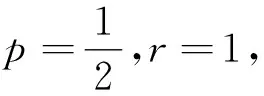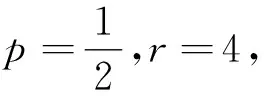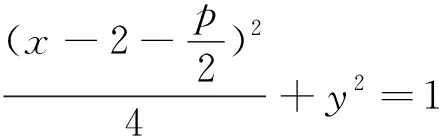从一道模拟题谈抛物线与其根轴圆的位置关系

福建省仙游县华侨中学 (351251) 严志伟

1.试题呈现

如图1,抛物线y2=8x与动圆M:(x-8)2+y2=r2(r>0)交于A,B,C,D四个不同点.(1)求r的取值范围;(2)略.

2.探究一般性结论

对于一般的抛物线C:y2=2px(p>0),动圆M:(x-a)2+y2=r2(r>0),有什么类似的结论?

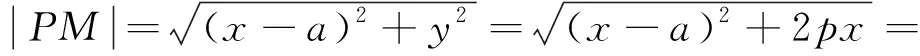
若a-p≤0,即a≤p,则当x=0时,|PM|取最小值|a|.这时若r=|a|,则抛物线C圆与圆M相切于顶点,且这两曲线有且仅有这一个公共点;

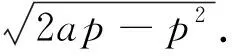
命题1 抛物线C:y2=2px(p>0)与动圆M:(x-a)2+y2=a2(a≤p)相切于原点,且无其他公共点;抛物线C:y2=2px(p>0)与动圆M:(x-a)2+y2=2ap-p2(a>p)相切于两点,两切点的横坐标都是a-p,且无其他公共点.

由此容易得到

推论1 对于抛物线C:y2=2px(p>0)和动圆M:(x-a)2+y2=r2,

1. 若a≤p,则

(1)r<|a|⟺抛物线C与动圆M有0个公共点;

(2)r>|a|⟺抛物线C与动圆M有2个公共点(均为非切点).

2. 若a>p,则

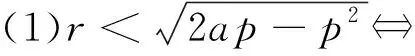
(2)r>a⟺抛物线C与动圆M有2个公共点(均为非切点);

(3)r=a⟺抛物线C与动圆M有3个公共点(1个切点,即原点,2个非切点);

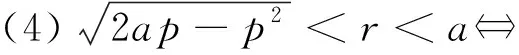
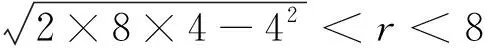
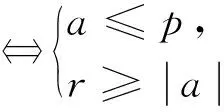
类似地,有

命题2 抛物线C:x2=2py(p>0)与动圆M:x2+(y-b)2=b2(b≤p)相切于原点,且无其他公共点;抛物线C:x2=2py(p>0)与动圆M:x2+(y-b)2=2bp-p2(b>p)相切于两点,两切点的纵坐标都是b-p,且无其他公共点.

推论1 对于抛物线C:x2=2py(p>0)和动圆M:x2+(y-b)2=r2,

1.若b≤p,则

(1)r<|b|⟺抛物线C与动圆M有0个公共点;

(2)r>|b|⟺抛物线C与动圆M有2个公共点(均为非切点);

2.若b>p,则

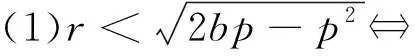
(2)r>b⟺抛物线C与动圆M有2个公共点(均为非切点).

(3)r=b⟺抛物线C与动圆M有3个公共点(1个切点即原点,2个非切点);

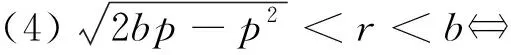
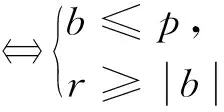
3.探究结论的应用

上述结论揭示了抛物线与其根轴圆的位置关系.应用之可简捷解决有关的试题及数学问题.

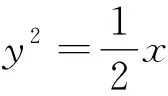
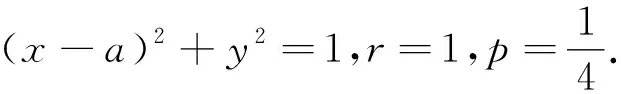
例2 (2011年全国高考重庆卷)设圆C位于抛物线y2=2x与直线x=3所围成的封闭区域(包含边界)内,则圆C的半径能取到的最大值为________．

例3 若酒杯的轴截面为抛物面,其边界的方程为x2=4y,一个半径为r的小球置于酒杯中,当r的范围为多少时,球可触及酒杯底部?

简析：本题实质上是求抛物线x2=4y与圆x2+(y-b)2=r2(b>0)相切于抛物线的顶点(坐标原点)且无其他公共点时r的范围.据命题2,r=b>0且b≤p=2,即0

例4 (1983年全国高中数学联赛试题)设M={(x,y)|y≥x2},N={(x·y)|x2+(y-b)2≤1}且M∩N=N,求实数b的取值范围.

例5 (日本中央大学自主招生试题)求抛物线x2=y与圆x2+(y-b)2=16公共点的个数.