巧用曲线系探索一类斜率比值问题*

福建省泉州市第七中学 (362000) 林景芳 林志敏

题目(2022年全国甲卷·理20)设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过F的直线交C于M,N两点．当直线MD垂直于x轴时,|MF|=3．(1)求C的方程;(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β．当α-β取得最大值时,求直线AB的方程．

分析：(1)y2=4x,过程略;(2)求α-β的最大值,关键是解决倾斜角β,α的关系,进而转化为寻找tanα,tanβ即kMN,kAB的关系.

本题涉及的是直线与抛物线问题,计算相对简单,如果把曲线改为椭圆或双曲线,计算量将大大增加,为了更好解决这类问题并加以推广,本文着重介绍曲线系的解题方法.

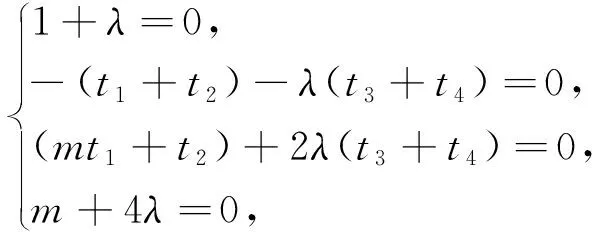
评注：本题涉及的是蝴蝶型斜率比值为定值与直线过定点之间的关系,我们把问题一般化,便于探索其内在联系.

图1

图2

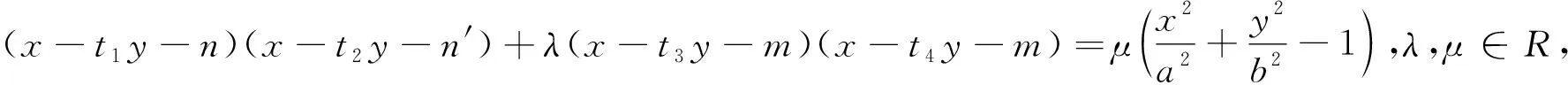
图3

以上从曲线系的解题视角证明并推广了一类斜率比值及定点问题,它也是解析几何的热点问题和常见模型,挖掘其内在联系并加以推广,具有重要意义.实际上,本文得到的三个结论,也是蝴蝶定理和坎迪定理在解几中的一个具体应用.