一道圆锥曲线题的解法探究与推广*

聊城大学数学科学学院 (252000) 徐茂林 房元霞

数学的问题从解法来分就是两类:一类方法唯一,多题一解;一类方法两种或两种以上,一题多解.多题一解从通性通法的角度考察对知识的本质性认识;一题多解则要求学生打破常规刻板的解题思路,从不同的思维方向对同样条件进行整合.多题一解重视学生基础,而一题多解,则会培养学生的发散性思维.下文以一道求定点问题为例,探求一题多解奥秘.

1 原题呈现

(1)求椭圆C的标准方程;

(2)若椭圆上一顶点A(-2,0),直线l:y=kx+m与C交于两点P、Q,且AP⊥AQ,试判断直线l是否过定点?若是,求出此定点的坐标;若不是,请说明理由.

2 解法探究

思路1 若直线l过定点,可看作过该点的直线系,所以直线l在y轴上的截距m随斜率k的变化而变化.因此,找到二者的变化规律,确定过定点的直线系方程,即可找到定点.

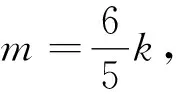
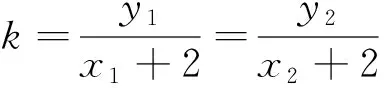
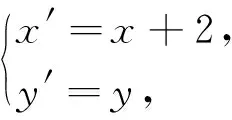
思路3 前两种解法以直线的一般式方程进行计算,或最后回归到一般式方程;回想教材中直线方程有几种不同的形式,我们思考能否从直线方程的另一形式运算求解?分析后发现,应该可以利用两点式,P、Q是直线l上的两点,从直线l的斜率或倾斜角两个角度求出定点.

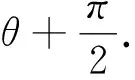
思路4 在高中阶段,二次曲线系属于拓展内容,圆、椭圆、双曲线、抛物线都属于二次曲线,两条直线也被称为退化的二次曲线.从两条直线出发,我们能否用类似曲线系的方法,求出定点?

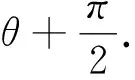
3 推广探究

若将题目中A点一般化为椭圆上任意一点,并将两直线AP、AQ的斜率之积一般化,可将结论推广至双曲线与抛物线.

图1

图2

图3