盾构先行刀切削深度计算模型研究

张存斌

（中铁十四局集团有限公司，山东 济南 250014）

1 先行刀切削土体过程分析

1.1 刀具组合切削过程分析

先行刀与切刀的组合布置中，先行刀高度（此处的高度指的是刀具高于盾构辐条平面的距离，切刀相同）要高于切刀高度，并且先行刀高度往往也不止一种。采用刀具不同高度的布置形式，可充分发挥不同刀具的作用，优化盾构掘进效率[1-2]。在该刀具布置下，当刀具作用于刀盘前方土体（下文简称“掌子面”）时，先行刀先接触掌子面，在掌子面上形成一系列同心圆的沟槽，然后切刀继续对掌子面进行开挖，2种刀具组合作用完成掌子面原状土体的切削。被切削剥落的土体随着刀盘的转动与改良材料充分混合，形成流塑性良好的渣土，填充在刀盘辐条之间的空隙及土仓之中，支撑掌子面。由此可知，在盾构掘进过程中，刀具不仅切削掌子面的原状土体，同时还会对先行刀剥落后的渣土进行切削。因此，在进行刀具扭矩计算或刀具磨损分析等与刀具相关的研究时，须分别考虑2种不同种类的土体。

1.2 先行刀运动简化

为了研究先行刀的切深，需要先对先行刀的运动轨迹进行分析。在盾构掘进过程中，先行刀的运动由2个部分组成：沿着盾构掘进方向的直线运动、垂直于隧道轴线方向的转动。为方便分析，将先行刀简化为一个点，则其运动方程如公式（1）所示。

式中：v为盾构掘进速度；w为刀盘转速；t为时间；r为先行刀轨迹半径。

显而易见，先行刀的运动为三维螺旋线运动。为了更直观地对先行刀切深进行计算，从先行刀角度出发，将先行刀垂直于隧道轴线方向转动的二维圆周运动简化为一维直线运动的方式，将三维运动简化为二维运动。当先行刀完成一个圆周的循环运动时，其在x方向上行进了贯入度长度的距离，在zy平面上回到初始位置，在简化过程中将先行刀转动过程中zy这2个方向的运动等效为y方向上的直线运动，同时x方向上的运动方程不变，最终将先行刀的三维运动转化为二维运动。先行刀简化的二维运动方程如公式（2）所示。

式中：v为盾构掘进速度；w为刀盘转速；t为时间；r为先行刀轨迹半径。

1.3 单把先行刀切深分析

在对先行刀的切深进行分析前，需要先明确先行刀“切深”的概念。在该文的论述中，先行刀的切深为先行刀切削形成的新掌子面与先行刀切削前掌子面之间盾构掘进方向上的差值，即切深代表的含义为先行刀切削原状土的深度，而非切削原状土体与改良后渣土的总深度。

对先行刀运行轨迹进行简化后，先行刀的运动轨迹为2个方向的直线运动组合。先对轨迹上只存在一把先行刀的情况下的先行刀切深的问题进行分析。根据工程实际情况，同时为简化计算，该文提出如下假定：1）先行刀切削土体过程中，仅切削先行刀轨迹宽度内的土体。2）先行刀开挖形成的新的自由面，不会因土仓压力及地层应力等外力而发生变形。3）盾构处于直线掘进状态，无上下坡及曲线运动。4）盾构掘进过程中贯入度恒定。

从盾构始发状态开始对先行刀切削掌子面的过程进行分析。随着盾构始发先行刀接触掌子面，并以一定的角度γ（γ与先行刀所处的轨迹半径及盾构掘进的贯入度有关，如公式（3）所示）相对于掌子面运动。随着刀盘转动，先行刀切削土体的切深不断增加。当先行刀完成一个圆周切削（在简化二维运动方程中表现为先行刀在y方向运动2πr距离，即从位置A到达位置B）时，先行刀切深达到最大值a。由于在简化过程中将二维的圆周运动简化为一维的直线运动，因此把第一个切削循环开挖土体在相应位置标出，如图1所示。接着对第二个切削循环进行分析，在第二个切削循环（位置B到位置C）中先行刀切深为盾构掘进贯入度a。

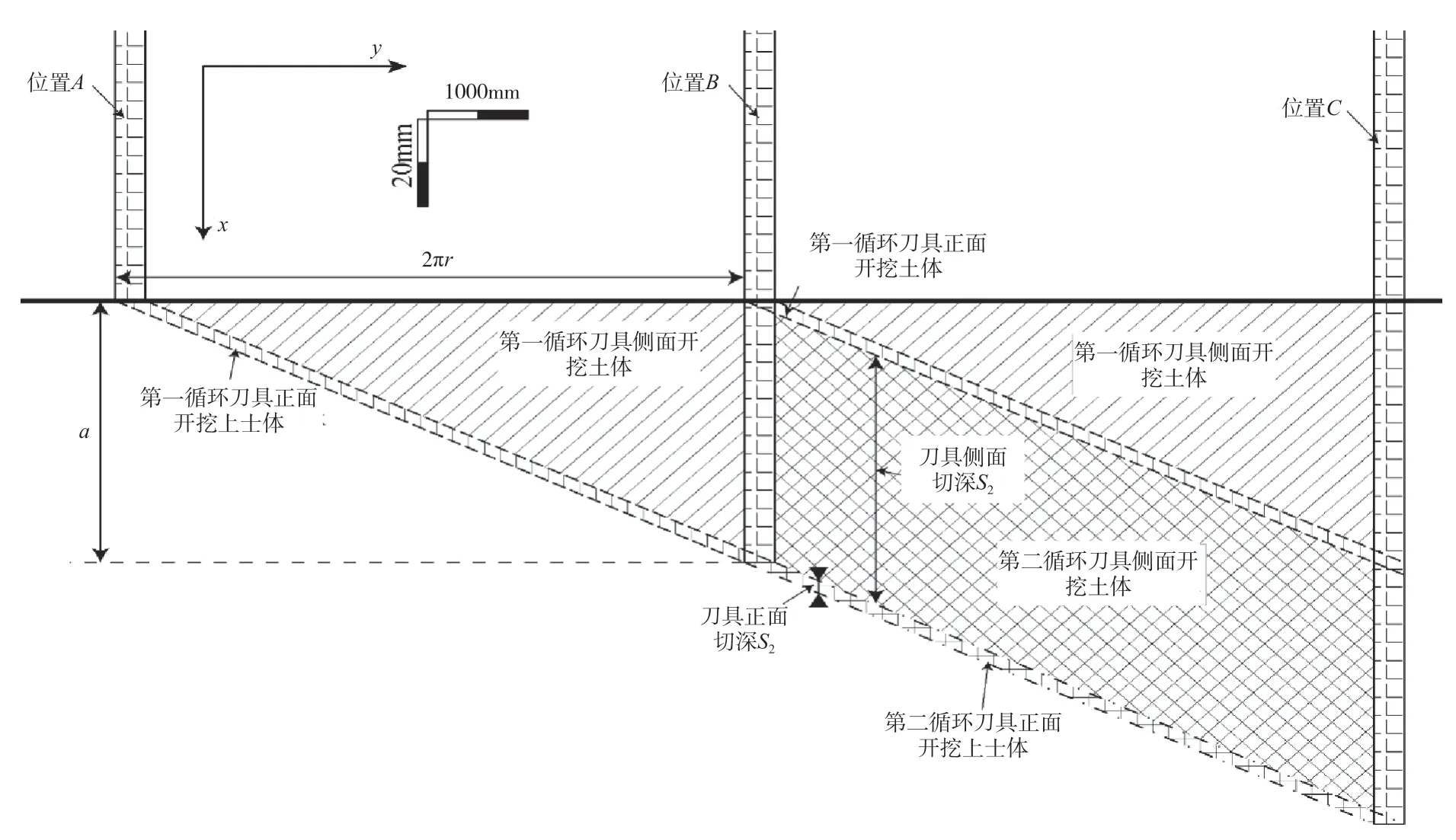
图1 先行刀切削过程

式中：a为盾构掘进贯入度；r为先行刀运行轨迹半径。

1.4 先行刀长度对切削土体的影响

由图1可知，先行刀切削土体主要由先行刀侧面及正面组合完成。假定先行刀侧面切削土体的深度S1、先行刀正面切削土体的深度S2，则先行刀的切深为S1+S2。令先行刀长度L为300mm，先行刀高度h为190mm，先行刀轨迹半径r为1000mm，盾构掘进贯入度a为60mm，利用公式（4）对先行刀各部分的切深进行计算，得S1、S2分别为57.13mm、2.87mm，S1约为S2的19.91倍，即原状土体的开挖主要由先行刀侧面完成。

式中：a为贯入度；L先行刀长度；r先行刀轨迹半径。

实际工程中，先行刀长度L为150mm～375mm，先行刀的轨迹半径多在500mm以上，盾构掘进贯入度为40mm～100mm。先行刀正面的切削深度占先行刀总切削深度的比例随先行刀轨迹半径r、先行刀长度L的增大而减小（如图2所示）。当轨迹半径大于1000mm、刀具长度小于375mm时，先行刀正面切深占比小于6%，因此对先行刀组合配置情况下的先行刀的切深进行分析时，为方便计算，可忽略先行刀长度的影响。

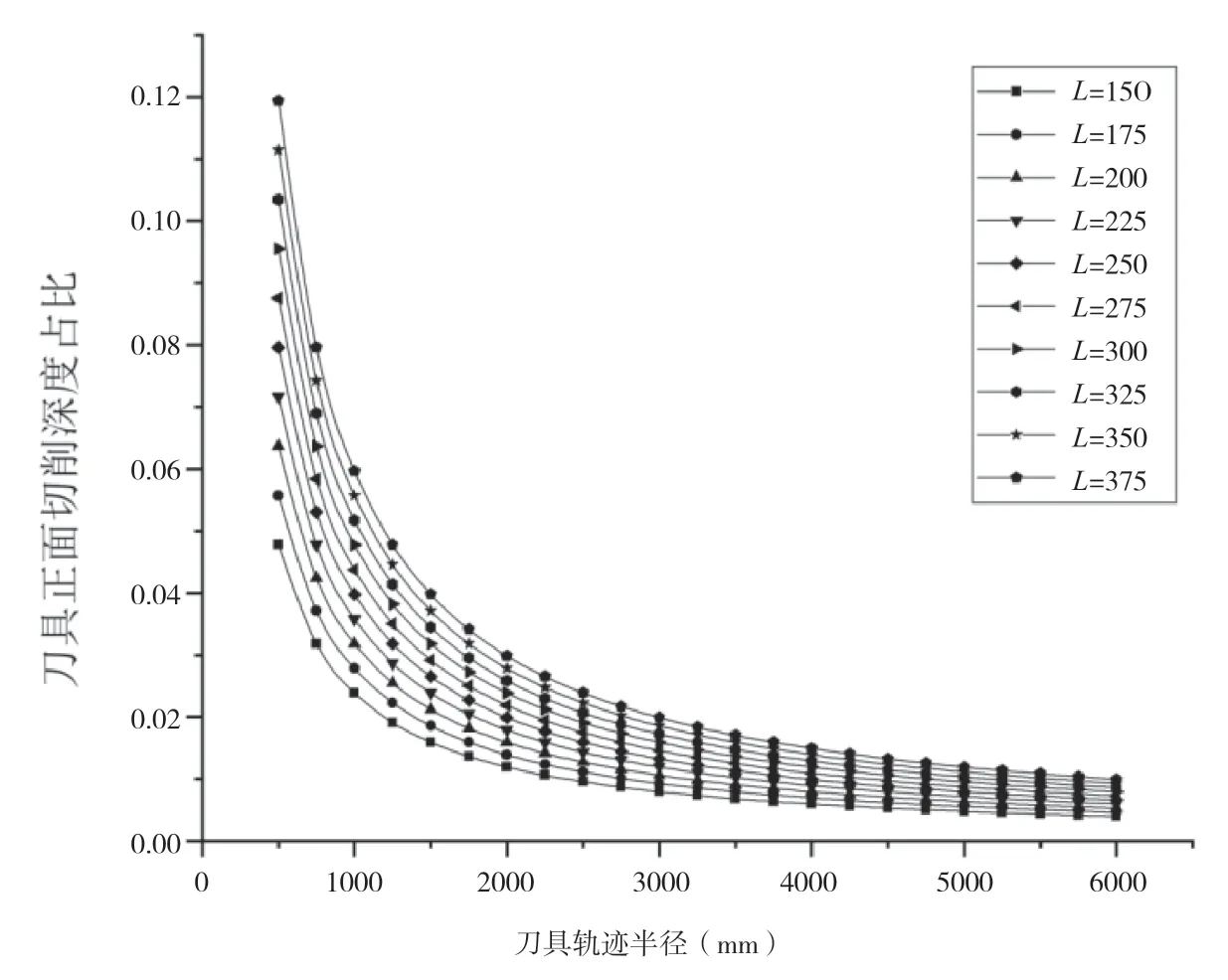
图2 先行刀正面切深变化

2 组合形式对先行刀切深的影响

由第1.3节可知，当统一轨迹中只有一把先行刀时，其切深为贯入度，接下来对不同先行刀组合形式下的各个刀的切深进行分析。

2.1 等高布置下先行刀切深分析

先来分析同一轨迹存在多把高度相同先行刀的情况下不同位置先行刀的切深，计算模型如图3所示。假设同一轨迹中存在3把先行刀，先行刀2与先行刀1、先行刀3的夹角（两先行刀中心与刀盘中心连线的夹角，下同）分别为β1、β2，则在简化模型中先行刀之间距离分别为rβ1、rβ2。以先行刀2为研究对象，对先行刀2的切深进行分析。

图3 较低先行刀的切深计算模型

与单把先行刀相似，当先行刀开始切削掌子面时，即先行刀开挖的第一个循环，3把先行刀切深不断增加。当先行刀2到达先行刀3起始位置时，先行刀2切深达到最大值。先行刀2的切深为先行刀2切削形成的掌子面与先行刀3切削产生的掌子面之间x方向的距离。当盾构进入正常掘进阶段时，先行刀2切深不再发生变化。分析可知，等高条件下，先行刀2切深由其旋转方向前方紧邻的先行刀与先行刀2之间的距离（在实际工程中表现为两先行刀的夹角β）决定，切深为βa/2π，与文献[3]的结果相同。

由计算模型可知，先行刀布置是其切深的决定性因素，而与以何种方式对其进行分析无关。在计算中无论先行刀是以123、312、231何种排列顺序进行分析计算，先行刀2的切深均相同。因此为简化组合布置的先行刀切深计算过程，后续计算中将需要分析切深的先行刀视为整个轨迹半径中的最后一把。

以上文总结的等高布置条件下3把先行刀切深的计算方法及原则为基础，将该方法扩展到多把先行刀的情况。假设同一轨迹上布置有n把先行刀，每把先行刀与前刀之间的夹角为βi。则有公式（5）。

则先行刀i的切深Si如公式（6）所示。

由公式（5）、公式（6）可知，当先行刀的布置为轴对称布置时，刀盘的正反转不影响对称轴上先行刀的切深，而会对不处于对称轴上的先行刀切深产生影响。

2.2 不等高布置下先行刀切深分析

上文已对等高先行刀布置条件下的先行刀切深进行了分析，但实际情况下先行刀往往是非等高的，先行刀高度分为多种，因此必须对不等高布置条件下先行刀的切深进行分析。

2.2.1 最低先行刀的切深分析

先对该轨迹中高度最小先行刀的切深计算模型进行分析。根据先行刀切深的定义，先行刀的切深为其形成的新掌子面与切削前掌子面之间x方向的差值。在计算模型中，切削前掌子面的形成可能是距先行刀A（需要进行切深计算的先行刀）最近的先行刀，也可能是距先行刀A较远的先行刀，各个差值中的最小值为对象先行刀的实际切深。

对简化模型进行分析。假设先行刀轨迹上存在3把先行刀：先行刀1（高度h1）、先行刀2（高度h2）、先行刀3（高度h3），且h1小于h2、h3。对先行刀1的切深进行分析，分析先行刀1、3形成的掌子面之间的差值S13，如公式（7）所示。

式中：S13为先行刀1相对先行刀3的切深；β13为先行刀1、3之间的夹角；a为贯入度；h13等于h3-h1，由于h1小于h2、h3，因此|h13|=h3-h1。

当S13大于0时，先行刀1的运行轨迹位于先行刀3的运行轨迹之下，先行刀1切削土体；当S13等于0时，先行刀1的运行轨迹与先行刀3的运行轨迹重合，先行刀1处于临界状态；当S13小于0时，先行刀1的运行轨迹位于先行刀3的运行轨迹之上，先行刀1不切削土体。

同理，可计算先行刀1相对先行刀2的切深S12。先行刀1的实际切深为其相对其他先行刀切深中的最小值，如公式（8）所示。

2.2.2 最高先行刀的切深分析

对较低先行刀的切深进行分析后，接下来采用相同方法对较高先行刀的切深进行分析。先行刀高度h1大于h2、h3。先行刀1的相对切深S1i如公式（9）所示，其与公式（7）具有相同的形式，先行刀的实际切深同样取相对切深中的最小值。

式中：S1i为先行刀1相对于先行刀i的切深；β1i为先行刀1、i之间的夹角；a为贯入度；h1i等于hi-h1，由于h1大于h2、h3，因此|h13|=h1-hi。

2.3 先行刀切深计算模型

先行刀的切深主要由同一轨迹上先行刀的高差、先行刀之间夹角、贯入度3个因素决定。假设同一轨迹中有n把先行刀，令需要计算切深的先行刀编号为1，其他先行刀沿刀盘转动方向依次命名为2，3，...，n，先行刀1的切深S1计算模型如公式（10）所示。

式中：β1i为先行刀i与先行刀1沿刀盘转动方向的夹角；hi为先行刀i的高度，h1i为hi-h1；a为贯入度；S1i为先行刀1相对于先行刀i的切深。

3 先行刀切深计算模型的应用

切深作为先行刀与土体作用中重要参数，其在盾构相关问题的研究中应用广泛，该文提出的切深计算公式可为相关研究提供一定的参考，例如先行刀切削力的精细计算、刀盘先行刀的布置优化和先行刀磨损分析等。

3.1 先行刀切削力计算

刀具的切削扭矩计算公式方面的研究有很多，文献[3-5]通过对刀具及被切削土体的受力分析，给出了刀具切削过程中的受力计算公式，如公式（11）所示。

式中：q为先行刀所受的平均阻力；p0为掌子面的静止土压力；c掌子面土体的黏聚力；φ为掌子面土体内摩擦角；Q为刀具受到的切削力；b为刀具的宽度；h为刀具的高度。

公式（11）推导的前提为刀具高度范围内，被切削的土体为均质。但根据该文的推导及施工经验，在盾构开挖过程中，被切削剥落后的土体与地层中的原状土体的性质之间存在差异。以此为基础对公式（11）进行优化，将刀具高度范围内切削的土体分为2该文部分，即原状土和剥落后的渣土，计算模型如图4所示，公式（12）为优化后的公式，公式中切削力的计算比原公式更接近使用的真实情况。

图4 先行刀切削力计算模型

式中：q为先行刀切削原状土的平均阻力；q'为先行刀切削渣土的平均阻力；c'、φ'分别为渣土的黏聚力及内摩擦角；h原为切削原状土的高度；h渣为切削渣土的高度。

3.2 先行刀磨损分析及布置优化

根据摩擦学原理及盾构刀具磨损机理的相关研究，刀具磨损的主要机理为磨粒磨损。磨粒磨损的相关理论中，影响磨损量的一个重要因素就是接触面的受力状态。

在北京地铁新机场线建设过程中，土压平衡盾构的刀具配置了先行刀及切刀2种刀具，先行刀配置的高度有2种，分别为145mm、175mm，同一半径中2种刀具等间距交错布置。对施工后刀具进行尺寸总结后发现，同一半径中145mm先行刀的磨损量明显低于175mm先行刀，甚至存在145mm刀具未发生磨损的现象。即当刀具布置存在高差时，不同高度刀具的磨损量存在较大差异，低刀的磨损量明显小于高刀。

结合刀具切深计算模型分析可知，在该种刀具布置情况下，盾构开始掘进时高刀同时切削掌子面原状土体及渣土，而低刀只切削渣土。由于渣土的密实度等指标要小于原状土，因此导致刀具切削过程中，高刀的磨损率明显大于低刀。随着不断磨损，高刀高度逐渐降低，当2种刀具的高差低于一定值时，低刀开始切削原状土体，低刀的磨损率开始增加。当刀具到达失效标准时，高刀的磨损量要明显大于低刀。

基于等寿命原则，进行先行刀设计及刀盘刀具布置时，应将切深作为一个重要的影响因素，保证各个位置刀具寿命基本相同，同时满足施工高效性及工程经济性的要求。该文总结的先行刀切深计算模型可为先行刀切深计算提供一定的理论依据。

4 结论

首先，在盾构施工过程中，先行刀为三维的螺旋线运动，先行刀运动过程中切削土体分为原状土体及剥落后土体2个部分，各部分占比与先行刀切深有关。

其次，运行轨迹中只存在一把先行刀时，先行刀的切深为盾构掘进的贯入度，并且先行刀侧面为切削土体的主要作用面，绝大多数情况下侧面切深占总切深的94%以上。

再次，运行轨迹中存在多把先行刀时，先行刀的切深由该轨迹中先行刀布置、盾构贯入度决定，决定因素为先行刀所处位置之间角度差及先行刀高度差，刀盘旋转方向不影响刀盘对称轴上先行刀的切深。

最后，先行刀切深计算模型可提高刀具切削力计算的精确性，并可为先行刀设计及刀盘刀具布置提供一定的依据。