基于时空融合技术的高精度遥感蒸散计算

戴肖杰, 范晓梅, 闵彤

(南京信息工程大学地理科学学院, 南京 210044)

蒸散作为水循环和气候系统的中心过程,它不断驱动着气候系统,在地表能量平衡和水量平衡中具有举足轻重的地位[1-2]。蒸散代表着生态系统功能、气候、碳反馈及水循环之间的联系,它在水量预测、干旱分析、气候变化以及环境监测等方面发挥着不可替代的作用[3]。因此,精确量化蒸散的时空动态对于理解气候变化和优化水资源管理具有相当重要的意义。

近几十年,遥感技术的进步为区域蒸散的反演提供了新的可能,利用遥感反演蒸散已成为估算区域和全球蒸散最常用的手段[4]。目前,基于能量平衡原理的地表能量平衡系统(surface energy balance algorithm for land,SEBAL)[5]、SEBS(surface energy balance system)[6]等蒸散模型应用较为广泛。SEBS模型除物理机理明确、计算简单外,该模型还提出了参数化方案,能够准确地计算热量粗糙长度,比其他蒸散模型采用固定值更为精确,在中国北方和欧亚地区均有良好表现。Liaqat等[7]基于Landsat影像分别利用SEBS模型和METRIC模型对亚洲东北部地区的生态系统进行了蒸散的计算,并利用通量数据对结果进行了验证,结果表明SEBS模型具有更高的准确性。王晓勇等[8]基于SEBS模型对不同时期的海流兔河流域的蒸散进行量化,并结合长序列地下水监测数据和土地利用数据对不同土地类型转移量的地下水位及影响因素进行了分析。由此可见,前期的蒸散反演多采用MODIS或Landsat等单一遥感数据,而单一传感器往往存在一些无法避免的数据缺陷[9]。比如,Landsat数据虽然空间分辨率较高(30 m),但重访周期较长(16 d)且易受云雨天气干扰,常出现影像缺失问题,无法进行长时间动态监测。MODIS数据重访周期较短(8 d),但空间分辨率较粗(250～1 000 m),无法适用于范围较小且地表复杂条件下的蒸散研究。如何融合多源遥感数据发挥各自时空分辨率的优势,对于小区域的高精度蒸散反演具有重要的理论意义和应用价值。

时空融合技术通过建立高空间与高时间分辨率数据之间的变化关系,对高空间分辨率数据的空间细节特征与高时间分辨率数据的时间变化信息进行有机结合,是获取高时空分辨率遥感影像的有效方法[10]。目前,已有众多国内外学者对时空融合算法展开了研究。Gao等[11]提出一种时空自适应反射率融合模型(spatial and temporal adaptive reflectance fusion model,STARFM),该方法在地表均质性较高时性能表现良好,但在地表异质度较高的情况下,其预测精度会降低,且此方法难以预测地表的突变现象[12]。为了提高STARFM模型在复杂地表下的预测精度,Zhu等[13]提出了增强型时空自适应反射率融合模型(enhanced spatial and temporal adaptive reflectance fusion model, ESTARFM),该算法考虑了像元反射率的时间变化特征,能够有效捕捉地物剧烈变化特征,提高了复杂下垫面情况下地表特征参数的融合精度[14]。目前,时空融合算法已被广泛应用于植被物候、干旱和水体监测等诸多领域[15-17],在蒸散反演中也有良好表现。白亮亮等[18]基于Landsat系列数据和SEBS模型估算了河套灌区的蒸散量,并结合MODIS日蒸散数据,利用 ESTARFM 算法实现蒸散数据的空间降尺度,构建了河套地区高时空分辨率蒸散数据集。尉毓姣等[19]基于SEBS模型获取了南京地区Landsat空间尺度的蒸散数据,在此基础上,采用ESTARFM模型将蒸散结果与MOD16A2数据进行时空融合,并对模型的融合精度进行了评价。利用ESTARFM算法对 MODIS 蒸散产品进行降尺度,是获取高精度蒸散的有效手段,但由于MOD16A2数据对建设用地、水域等非植被像元赋予无意义数值,导致部分像元缺失,无法融合得到完整的蒸散数据。对于水体、滩涂分布较广的滨海地区而言,如何构建区域内高时空分辨率的遥感数据集获取较为完整的蒸散序列是当前研究中亟须解决的问题。

因此,现以地表高度破碎化的黄河三角洲为研究区,利用ESTARFM算法融合Landsat和MODIS数据,构建研究区具有高时空分辨率的遥感数据集,并采用SEBS模型计算了区域的日蒸散量。通过比较融合反射率与实际反射率之间的差异,评估ESTARFM算法的性能,并利用彭曼公式估算的参考蒸散量、通量站观测数据及蒸发皿实测数据,对融合模型估算的蒸散结果进行了验证,探讨融合算法和蒸散模型结合的可行性和精度,以期为黄河三角洲水资源保护和生态系统良性发展提供科学依据,并为地表类型复杂且高度破碎化区域的蒸散研究提供新的思路。

1 材料与方法

1.1 研究区概况

黄河三角洲位于山东省东营市境内的黄河入海口地区(118°31′E～119°18′E,36°55′N～38°16′N),是由黄河尾闾不断改道和泥沙淤积所形成的扇形地块[20],如图1所示。研究区地属温带季风型大陆性气候,四季变化明显,年平均气温11.7～12.6 ℃;年均降水量530～630 mm,70%分布在夏季,平均蒸散量为750～2 400 mm。区内地势整体呈西南高、东北低,平均高程在5 m以下,地下潜水普遍埋深较浅(平均埋深为1.14 m),且矿化度较高(含盐量平均值为14.3 g/ L)[21]。自20世纪70年代以来,受农田开垦、油田开发等人为因素影响,黄河三角洲天然湿地大幅减少,区内景观破碎化程度不断加重[22]。目前,黄河三角洲面临着淡水资源匮乏、土壤盐渍化严重、生态系统失衡等问题[23]。因此,准确地计算区域蒸散量分析其时空变化过程可为正确估算土壤水分、预测农田旱情的发生和生态变化提供重要信息,对指导农业灌溉与排水、提高水资源的利用率等有着重要的意义。

1.2 数据来源

1.2.1 遥感影像数据

(1)Landsat8 OLI数据来源于美国地质调查局网站(http://glovis.usgs.goc/),OLI传感器包括了ETM+传感器所有的波段,并对波段进行了重新调整,能够更好地避免大气吸收特征,OLI的第1～7波段空间分辨率为30 m,第10～11波段为热红外波段,空间分辨率为100 m,回访周期均为16 d。研究主要使用了OLI的第2～7波段来计算归一化植被指数NDVI、地表反照率等参数,并基于OLI的热红外波段采用单窗算法[24]来反演地表温度。经筛选,2019年11月—2021年1月共有15期质量较好(云量小于10%)的Landsat影像见表1。采用 ENVI 软件进行影像的辐射校正、大气校正和图像裁切等预处理工作,地表参数的计算通过波段运算工具完成。

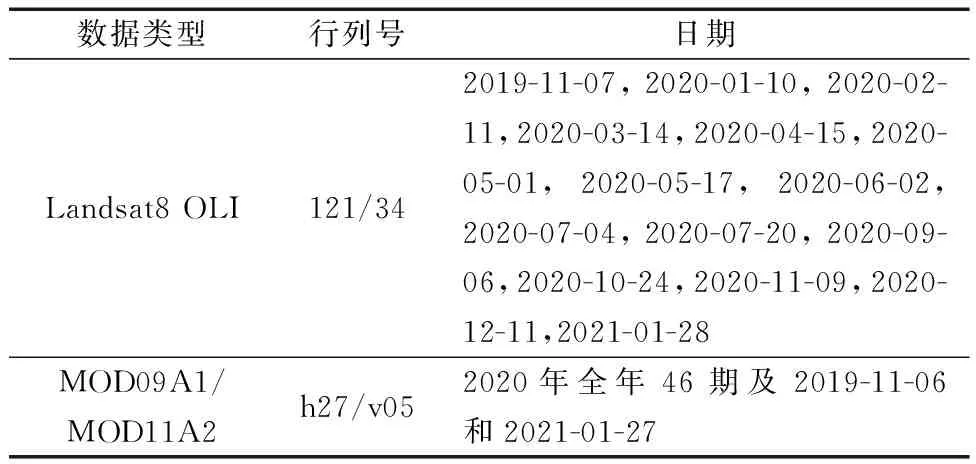
表1 遥感数据类型及获取日期Table 1 Remote sensing data types and acquisition date

(2)MOD09A1产品提供了7个波段的地表反射率,空间分辨率为500 m,回访周期为8 d。MOD11A2数据是MODIS地表温度产品,空间分辨率为1 000 m,时间分辨率为8 d。MOD09A1、MOD11A2数据均来源于美国航天局网站(https://urs.earthdata.nasa.gov/)。由于MOD09A1、MOD11A2为正弦曲线投影,利用MRT软件将两种MODIS产品重投影至与OLI数据一致的UTM-WGS84坐标系,并将其空间分辨率统一采样为 30 m,对MODIS和OLI数据进行空间配准及波段匹配处理,以便后续进行数据融合。MOD09A1和Landsat8 OLI的波段对应关系如表2所示。

表2 MOD09A1和Landsat8 OLI 波段对应关系Table 2 Band correspondence between MOD09A1 and Landsat8 OLI

1.2.2 专题数据

(1)气象数据。气象数据均下载于中国气象数据网(http://data.cma.cn/),选取研究区垦利站的日气温、气压、风速等气象要素,作为SEBS模型的输入参数。选取日照时数、日平均气温、相对湿度等要素用于彭曼公式的参考蒸散量估算。

(2)通量站数据。通量站验证数据来源于国家生态科学数据中心(http://www.nesdc.org.cn/),山东禹城农田生态系统国家野外科学观测研究站的通量数据产品是利用 ChinaFLUX技术体系进行标准化的质量控制和数据处理后的通量日值数据。

(3)土地利用类型数据。在参考研究区已有土地利用类型图的基础上,根据黄河三角洲2020年一期Landsat8 OLI遥感影像,按照自然资源部土地分类标准分类并制作了研究区的土地利用现状图,如图2所示,主要包括林地、水体、滩涂、农田、芦苇沼泽和建设用地6种土地利用类型。课题组又在2022年5月通过野外调查,对土地利用图分类的准确性进行了验证。

图2 2020年黄河三角洲土地利用分布Fig.2 Land use distribution in the Yellow River Delta in 2020

2 研究方法

研究基于ESTARFM算法和SEBS模型获取了黄河三角洲较高时空分辨率的蒸散数据,并对蒸散的时空格局及典型地物的蒸散特征分析,技术流程如图3所示。主要步骤如下:①首先对MODIS和Landsat遥感影像进行预处理;②利用ESTARFM算法生成高时空分辨率遥感数据集;③2020年黄河三角洲地区ET的计算和验证;④结合土地利用数据分析黄河三角洲蒸散时空格局及典型土地利用的蒸散特征。

NDVI为归一化植被指数;LAI为叶面积指数;ALBEDO为地表反照率;LST为地表温度;FVC为植被覆盖度图3 技术流程图Fig.3 Technical flowchart

2.1 时空融合算法

使用的时空融合算法是由Zhu等[13]提出的增强型时空融合模型(ESTARFM),该模型不仅考虑到了像元反射率的空间可变性、中心像元与周围像元的光谱相似性、还考虑到了不同时相上反射率值的变化,并使用滑动窗口的方法来抑制低空间分辨率影像的边界效应,有效提高了融合精度。该模型通过输入两个时相的Landsat数据和MODIS数据,以及一个预测时相的MODIS数据,从而生成预测时相的Landsat数据。融合过程忽略了影像的几何校正和大气校正的误差,首先确定搜索窗口大小,根据空间、光谱相关性使用搜索窗口在两期Landsat反射率数据中搜索与中心像元光谱特征相似的像元,然后结合两期MODIS反射率数据赋予每个相似像元距离权重和转换系数,通过权重来分配相似像元对中心像元的贡献率,再根据以上两期及预测期的MODIS数据计算时间权重,最后加入MODIS数据获取的时间关系系数,生成预测时期的Landsat尺度反射率数据。预测时期反射率的具体计算公式如下。

R(xω/2,yω/2,tp,B)=TmRm(xω/2,yω/2,tp,B)+

TnRn(xω/2,yω/2,tp,B)

(1)

Rk(xω/2,yω/2,tp,B)=RL(xω/2,yω/2,tk,B)+

RM(xi,yi,tk,B)]

(2)

式中:R为最终预测时期的高分辨率反射率;ω为相似像元搜索窗口,主要由地物类型的异质性所决定,这里取50个Landsat像元大小范围;tp为预测影像时期;B为遥感影像的B波段;Rm、Rn分别为Tm、Tn时期融合影像的反射率;Rk为Tk时期预测的高分辨率影像的反射率,k=m,n;RL、RM分别为Landsat影像、MODIS影像反射率;(xω/2,yω/2)为中心像元位置;(xi,yi)为第i个相似像元位置;N为相似像元的数量;Wi为综合权重因子;Vi为转换系数。

Tm和Tn时期的时间权重Tk,根据tk(k=m,n)时期与预测时期tp之间的反射率变化幅度由式(3)计算而来。

Tk=

(3)

2.2 蒸散量计算方法

所使用的蒸散量计算方法是地表能量平衡系统模型(SEBS),它是目前应用比较广泛的单层能量平衡模型之一。该模型具有坚实的理论基础,物理机理明确,而且考虑的气象要素较少,便于应用。SEBS模型的基本理论依据是地表能量平衡方程,在某一时刻的地表能量可表示为

Rn=G+H+λE

(4)

式(4)中:Rn为净辐射通量,W/m2;G为土壤热通量,W/m2;H为显热通量,W/m2;λ为水的汽化潜热,J/kg;E为瞬时蒸散量,kg/(m2·s);λE为潜热通量,W/m2。

SEBS模型采用地表能量平衡指数法来确定蒸发比,根据地表能量平衡方程,当地表处于极度干燥状态下,其潜热通量为零,此时显热通量为最大值,Hdry可表示为

Hdry=Rn-G

(5)

在地表极湿润环境下,土壤水分供应充足,此时显热通量为最小值,Hwet可表示为

Hwet=Rn-G-λEwet

(6)

极湿润条件下的潜热通量λEwet可以根据Peman-Monteith方法[25]求得。

相对蒸散比可以由实际显热与干、湿限显热的关系得到,即

(7)

最终蒸发比定义为实际蒸散与可用能量之比,计算公式为

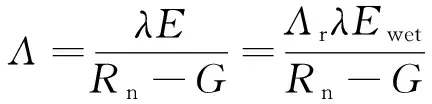
(8)

从而得到瞬时蒸散量为

Eins=Λ(Rn-G)/λρw

(9)

式(9)中:ρw为水密度,kg/cm3。

2.3 时间尺度扩展

2.3.1 日尺度蒸散扩展

通过SEBS模型获取的是卫星过境时刻的瞬时蒸散量,但在实际研究中长时间尺度的蒸散量才更有意义。假设能量通量在一天中会发生变化,但各组分之间的比例即蒸发比在一天中保持不变,因此日平均蒸发比就等于过境时刻的瞬时蒸发比。日蒸散量计算公式为

ETd=8.64×107Λ(Rnd-Gd)/λρw

(10)

式(10)中:ETd为日蒸散量,mm;Λ为日均蒸发比;Rnd为日净辐射;Gd为日土壤热通量;λ为水的汽化热量,J/kg。

2.3.2 月尺度蒸散扩展

月尺度蒸散的扩展借鉴了日尺度蒸散扩展的思想,Du等[26]认为,某一天的实际蒸散ET与日参考作物蒸散ETr之间的比值是不变的。通过计算某一天晴空遥感影像的ET与ETr之间的比值EFd,并以该比值作为某段时间内的特征值来计算这一段时间内的实际蒸散。其计算公式为

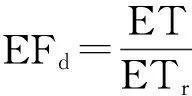
(11)

日参考蒸散量由世界粮农组织推荐的FAO56 Penman-Monteith[27]公式计算得,即

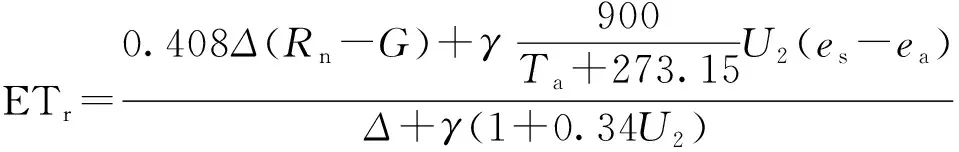
(12)

式(12)中:ETr为参考蒸散量,mm;Rn为净辐射通量,W/m2;G为土壤热通量,W/m2;Ta为大气温度,℃;U2为2 m高处的风速,m/s;es为平饱和水汽压,kPa;ea为实际水气压,kPa;Δ为饱和水汽压与温度的曲线斜率,kPa/℃;γ为干湿常数,kPa/℃。

通过ESTARFM算法获得了时间分辨率为8 d的Landsat数据,因此式(13)中的ET8dr为8 d累积的参考蒸散量,而8 d的实际蒸散量的总和为

ET8d=EFdET8dr

(13)

2.4 精度评价方法

2.4.1 融合算法精度评价

为验证融合算法的性能,选取2020年4月15日、5月17日和6月2日的影像作为实验,随机选取研究区内的40 000个像元对融合反射率与实际反射率进行对比,得到各日期不同波段的拟合曲线,并使用相关系数R、均方根误差RMSE、平均相对误差MRE对融合影像的质量进行评价。

(14)

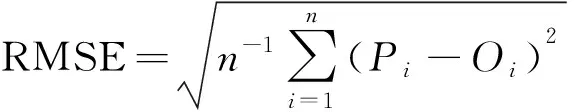
(15)

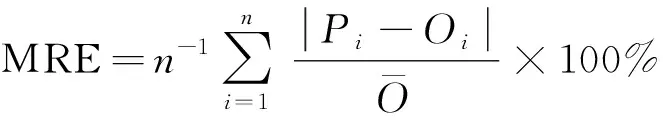
(16)

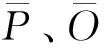
2.4.2 蒸散结果精度评价

研究区日蒸散结果的总体精度采用彭曼公式估算的日参考蒸散量进行验证,对比融合蒸散与参考蒸散量的变化过程,并对二者进行线性拟合,采用R、RMSE评价了融合蒸散结果的可靠性。

研究区地表覆盖类型复杂且破碎化程度较高,对区域内每种覆盖类型的蒸散结果进行验证较为困难,由于研究区内农田和水体分布范围较广,二者的面积占比分别达到了29.1%和27.3%,所以研究重点对区域内农田和水体的蒸散计算结果进行验证。研究区内缺少通量站数据,而禹城农田观测站与研究区基本处在同一纬度,同位于鲁西北平原和黄河下游引黄灌区,距离研究区仅200 km,水热条件和地表环境与研究区基本一致,因此采用禹城站观测的显热通量与研究区农田生态系统的瞬时显热通量进行线性拟合,并利用R、RMSE验证农田蒸散的计算精度。水体蒸散的验证采用垦利气象站的蒸发皿数据进行,对比水体的估算值与蒸发皿折算数据的散点分布并利用R、RMSE评价水体蒸散结果的准确性。

3 结果与分析

3.1 影像融合结果及精度验证

将3个不同日期的Landsat影像和融合影像在标准假彩色合成下的图像(图4)进行对比(400像元×400像元),由图4可见,融合影像空间细节良好、地物纹理清晰,能够明显区分不同地物间的反射率差异,与原始Landsat影像的整体差异较小。植被、裸地等混合像元较少的单一地表,融合反射率变化较小,预测精度较高。居民区、建设用地等地物交汇区域,融合影像受Red波段和混合像元的影响,部分建筑物有些泛红。同时,ESTARFM算法假设像元反射率随时间变化稳定且随时间的变化是线性的,而在复杂地表下像元反射率的变化并非线性,这也可能导致融合影像的反射率变化。

图4 Landsat影像与融合影像对比Fig.4 Comparison of Landsat images and fusion images

对比融合影像各波段反射率与实际反射率之间的散点分布(图5),由图5可知,融合反射率与实际反射率散点均匀分布于1∶1线附近,各波段相关系数R均在0.91以上,平均相对误差MRE均小于15.3%,均方根误差RMSE接近于0。ESTARFM算法通过对移动窗口中的相似像素进行加权来提高中心像素反射率的预测性能,能够很好地反映空间变异性。总体来讲,ESTARFM算法在地表破碎、景观异质性较强的黄三角地区具有良好的适用性,融合精度能够满足后续研究需要。

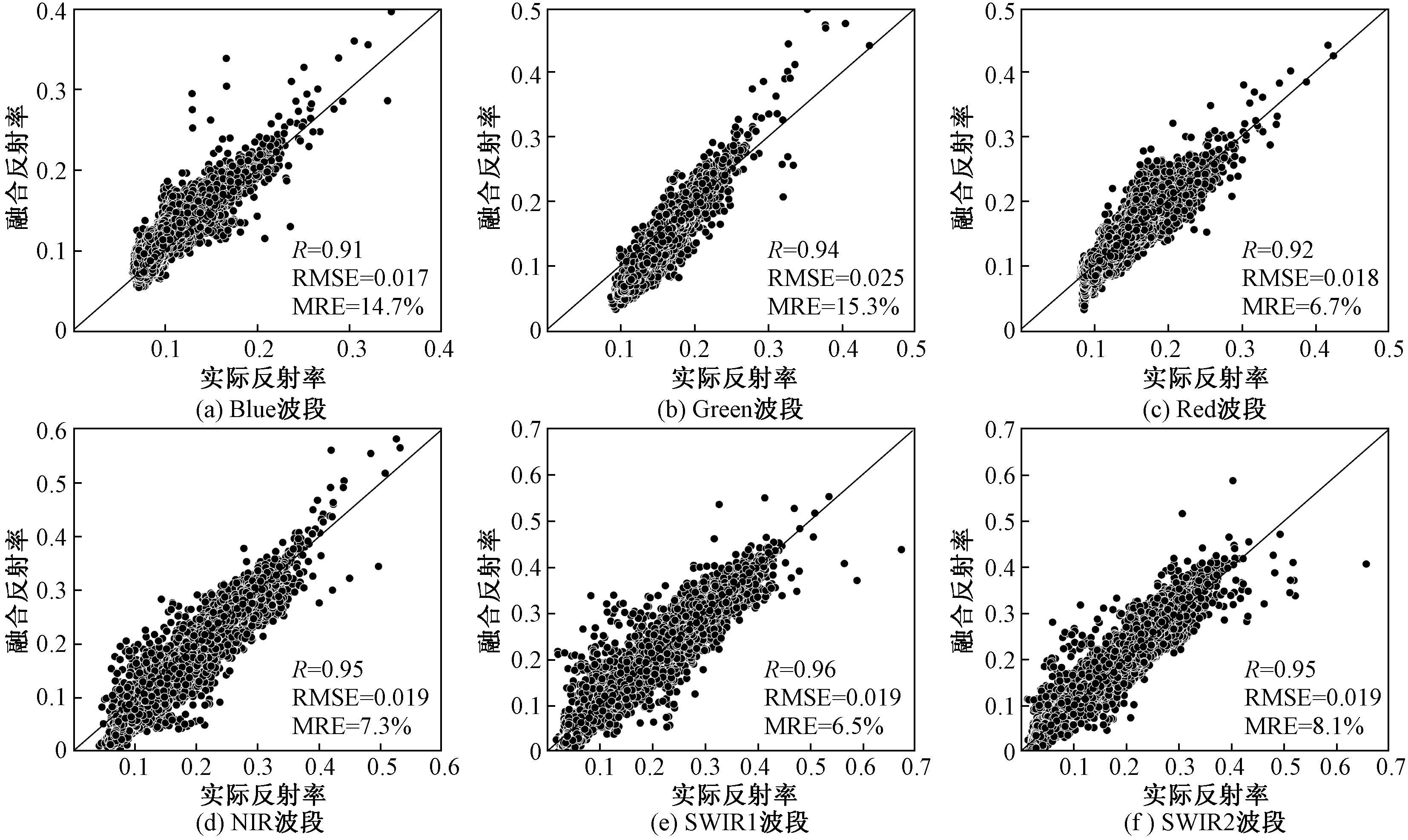
图5 融合反射率与实际反射率散点图Fig.5 Scatter plot of fusion reflectance with actual reflectance

3.2 蒸散结果及精度验证

基于融合得到的高时空分辨率遥感数据,利用SEBS模型计算日ET,并将日ET与彭曼公式估算的参考蒸散量及蒸发皿数据的变化过程进行对比(图6),由图6可见,模型计算的日蒸散量与蒸发皿数据、参考蒸散量的变化过程基本一致。但受到降雨天气的影响,导致融合蒸散与蒸发皿数据之间存在部分的差异。

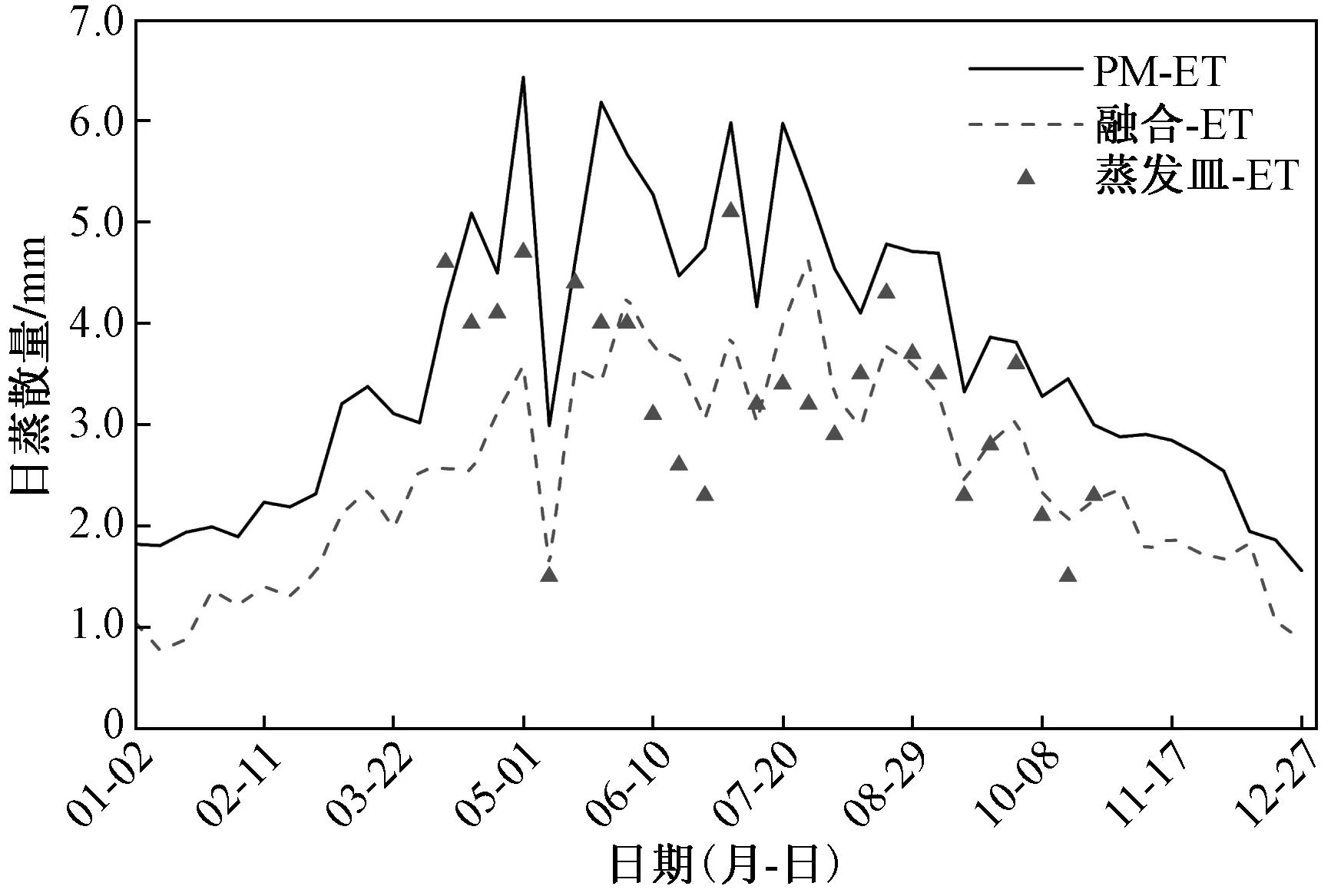
图6 SEBS模型计算的日蒸散量与日参考蒸散量及蒸发皿数据的对比Fig.6 Comparison between daily evapotranspiration calculated by SEBS model with reference evapotranspiration and pan data

将SEBS模型估算的瞬时显热通量与禹城站的显热通量数据进行对比,得到如图7所示的散点分布图。可见,模型估算结果与通量站观测值的拟合效果较好,相关系数达到了0.87,均方根误差仅为57.8 W/m2。将SEBS模型计算的水体日蒸散量与垦利站蒸发皿折算数据进行拟合(图8),模型计算的水面蒸发与蒸发皿折算的水面蒸发散点均分布于1∶1线两侧,相较于MODIS数据估算的水面蒸散结果,融合数据的水面蒸发与蒸发皿数据的相关系数R由0.87提升至0.93,均方根误差RMSE由0.44 mm/d下降至0.35 mm/d。ESTARFM算法和SEBS模型的结合不仅能够保证蒸散结果的计算精度,还能有效提高蒸散的时空分辨率。综上所述,利用MODIS和Landsat多时相遥感数据,基于 ESTARFM 算法和SEBS模型获得的高精度蒸散数据,避免了单一传感器和云雨污染的限制,能够满足地表破碎化地区的蒸散研究需求。

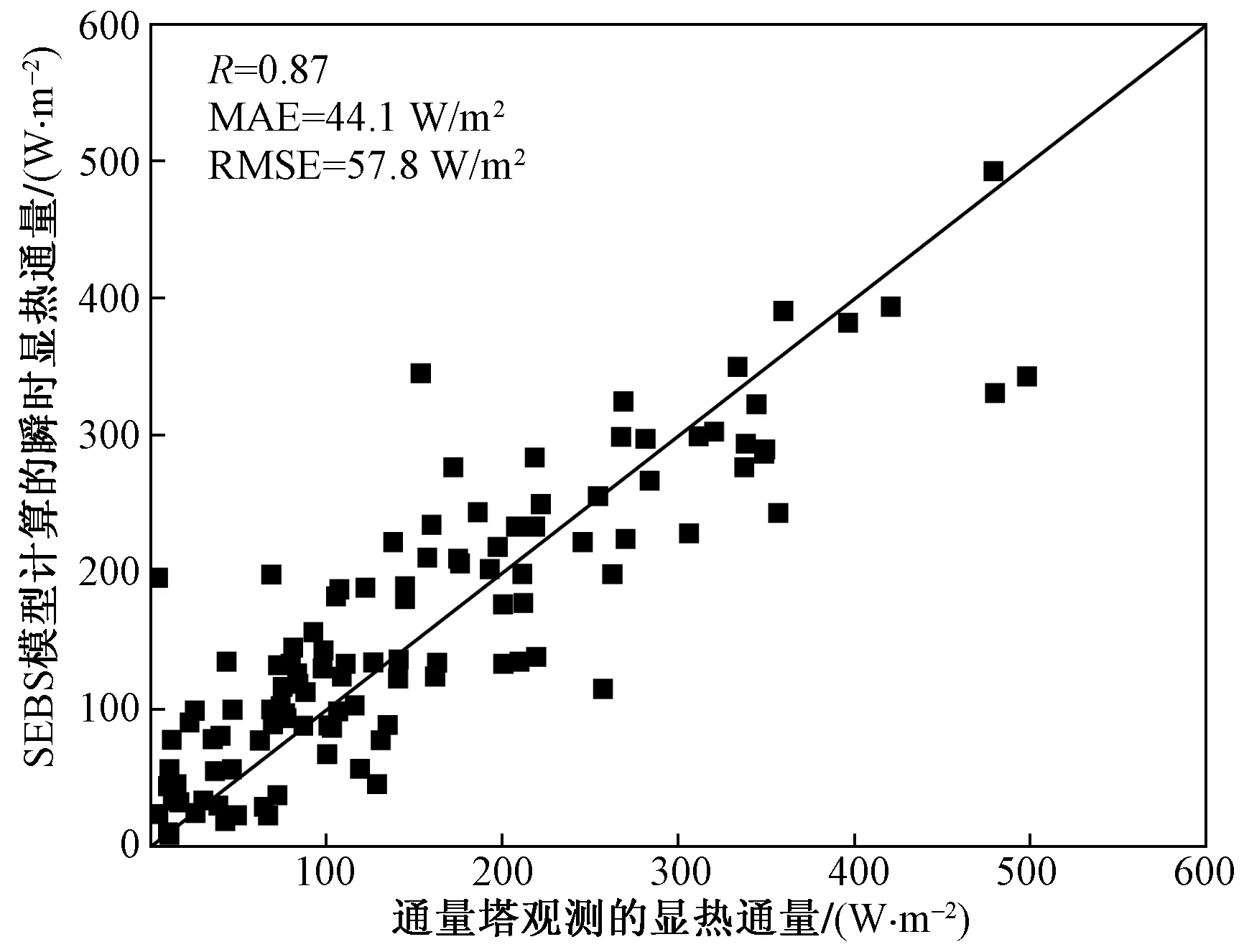
图7 SEBS模型计算的瞬时显热通量与通量塔观测数据对比Fig.7 Comparison of instantaneous sensible heat flux calculated by SEBS model with flux tower observation data

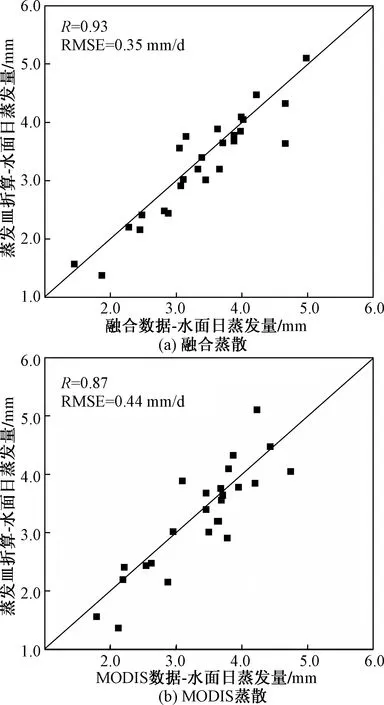
图8 SEBS模型计算的水面蒸发与蒸发皿折算数据的相关性分析Fig.8 Correlation analysis between water surface evaporation calculated by SEBS model and pan conversion data

3.3 蒸散时空格局

将研究区的月蒸散量叠加土地利用图,对区域蒸散的时空变化特征进行了研究(图9)。区域内蒸散随季节变化明显,总蒸散量的变化规律为:夏季>春季>秋季>冬季。春季(3—5月)气温回升,农田和湿地植被开始进入生长季,区内平均蒸散量大约为269.2 mm,标准差为36.9 mm,低值主要集中在黄河故道两岸的裸地和孤东等植被稀疏地区,而高值分布在沿海滩涂和水体等区域,海陆差异明显;夏季(6—8月)降水增多,土壤水分充足,植物进入生长季中期,部分农田和湿地植被的蒸散量超过滩涂和水体。区域平均蒸散量达到最大值(345.2 mm),与其他季节相比,其空间变化幅度较大,标准差为43.1 mm,低值主要集中在西南部的荒地和居民区等植被覆盖率较低的内陆区域;秋季(9—11月)区内平均蒸散量略低于春季,为248.4 mm,标准差为33.5 mm;冬季(12月—次年2月)由于气温较低,水循环缓慢,蒸散量较低,区内不同土地利用类型的平均蒸散量仅为99.4 mm,同时蒸散的空间变异性也较小,标准差仅为7.03 mm。由此可见,黄河三角洲各季节蒸散量空间分布特征较为相似,整体上由沿海滩涂向内陆逐渐减小,受到气温、降水和植被等因素影响,不同季节之间的蒸散量差异显著。

黄河三角洲典型地表覆盖类型的蒸散量如图10所示,可以看出,不同土地类型之间的蒸散量具有明显差异,总体表现为:水体>滩涂>林地>芦苇沼泽>农田>建设用地。水体的年蒸散量最大,达到了1 289.9 mm/a;由于滩涂位于潮浸地带,下垫面含水量较高,其年蒸散量仅次于水体,达到了 1 024.6 mm/a;林地的植被覆盖度较高,需水量与储水量较大,年蒸散量达到了971.3 mm/a;芦苇沼泽年蒸散量为884.4 mm/a,春季由于其植被覆盖度较低,蒸散量仅为241.5 mm,而夏季由于降水较多,植被生长旺盛,导致蒸散量显著增加(333.2 mm),秋季以后大部分芦苇枯萎或被收割因此蒸散下降至220.8 mm;由于研究区农田多为旱地作物,植被覆盖度不及林地和湿地植被,年蒸散量仅为 835 mm。农田在春季和夏季由于灌溉和降水的补充,下垫面供水充足,蒸散量和林地差距不大,但秋季以后由于作物收割导致蒸散量下降明显;建设用地由于其下垫面多为不透水面,导致四季的蒸散量都是最低,全年蒸散量为548.2 mm/a。

4 讨论

4.1 ESTARFM算法的不确定性分析

基于ESTARFM算法进行遥感数据的时空融合,结果表明,融合反射率与实际反射率之间的相关性均达到了0.85以上(表4)。ESTARFM算法能够充分利用像元之间的相似性并减小系统产生的误差,不仅能提升遥感数据的时空分辨率,同时还有较高的光谱还原度[28]。由表4可知,融合影像与实际影像在Blue、Green等波段的相关性接近0.95,而在SWIR1、SWIR2波段的相关性仅为0.9左右,这可能是由于不同传感器在光谱设置和光谱响应函数上有所差异,使得不同传感器之间存在系统性误差[29]。MODIS在SWIR1、SWIR2波段的空间分辨率仅为500 m,且OLI与MODIS传感器在SWIR1、SWIR2波段的光谱范围差异大于其他波段。另外,4月15日的融合精度(R=0.95)高于5月17日和6月2日(R=0.89和R=0.92),其原因主要是输入影像与融合预测影像的时间间隔不同。张晓川等[15]发现在融合过程中,输入数据与融合数据的日期间隔越短、输入影像质量越好,预测精度越高。相比于5月17日和6月2日的输入影像,4月15日的输入影像质量较好且与融合预测影像的时间间隔更短,地表类型变化更小,对应的光谱反射率更为相似。

表4 不同波段的反射率融合精度评价Table 4 Accuracy evaluation of fusion reflectance in different bands

相较于反射率的融合,地表温度的融合误差相对较大,众多研究[30-32]表明,低空间分辨率影像的像元边界、混合像元等问题会增加融合过程的不确定性。由于Landsat地表温度是利用热红外波段基于单窗算法反演得到,空间分辨率为100 m,而MOD11A2数据的空间分辨率仅为1 000 m,MOD11A2的低分辨率像元和边界效应会降低地表温度的融合精度[24]。总体来讲,ESTARFM算法在地表破碎的黄河三角洲地区具有良好的适用性,并且输入影像质量越高、距离预测日期越近,其融合精度越高。因此在研究中,应尽可能选择距离预测日期较近且质量较高的影像进行融合。

4.2 融合算法与蒸散模型结合的可行性分析

为探讨不同融合方案对最终蒸散结果的影响,设计方案一(先融合波段后计算蒸散)和方案二(先计算蒸散后进行融合)两种融合方案,并将融合结果与Landsat蒸散结果进行比较,系统评价两种融合方案的蒸散精度。

图11展示了两种融合方案的蒸散结果与原始Landsat蒸散结果对比,可见,两种方案的蒸散结果与实际Landsat蒸散在空间分布上都具有一定的相似性,但方案一的蒸散结果与Landsat计算的蒸散更为接近,二者日蒸散差值(图12)主要集中在 -0.4～0.4 mm/d,方案二的蒸散结果与Landsat蒸散的差值集中在-0.6～0.6 mm/d。将融合蒸散与Landsat蒸散进行线性拟合,由图13可见,相较于方案二,方案一的拟合效果更好(R=0.88),误差更小(0.36 mm/d)。该结果与Ke等[33]研究的结果一致,他们比较了与拟议方案一和方案二相似的3种融合方案生成的8 d 30 m蒸散数据,发现方案一的误差(RMSE<2.7 mm/8 d)总是小于方案二和方案三(RMSE<3.7 mm/8 d;RMSE<3.3 mm/8 d),并总结称降尺度后的蒸散与实际蒸散的一致性取决于地表参数反演的准确性,相较于先计算蒸散再进行融合降尺度,先融合出预测日期的反射率再计算蒸散更能提高蒸散的准确性。方案二在先进行蒸散计算时,由于MODIS影像的地表参数反演精度较低,且MOD11A2地表温度影像常存在边界模糊和像元缺失等问题,导致SEBS模型在估算中的不确定性增加,误差在后续的蒸散融合过程中会进一步增大[31]。而方案一先利用ESTARFM算法模拟出预测时期的高分辨率影像,能够最大限度地减小系统偏差并抑制低分辨率像元的影响[34],提高了地表参数的反演精度,使得蒸散的计算误差较小。

图11 融合蒸散影像与实际Landsat蒸散影像对比Fig.11 Comparison between fused evapotranspiration images and actual Landsat evapotranspiration image

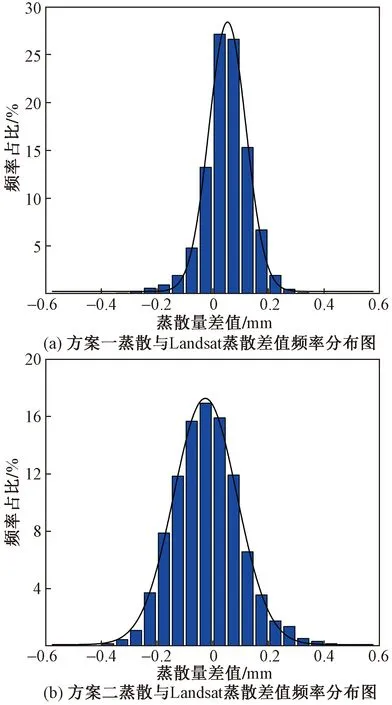
图12 融合蒸散与Landsat蒸散的差值频率分布Fig.12 Frequency distribution of difference between fusion evapotranspiration and Landsat evapotranspiration

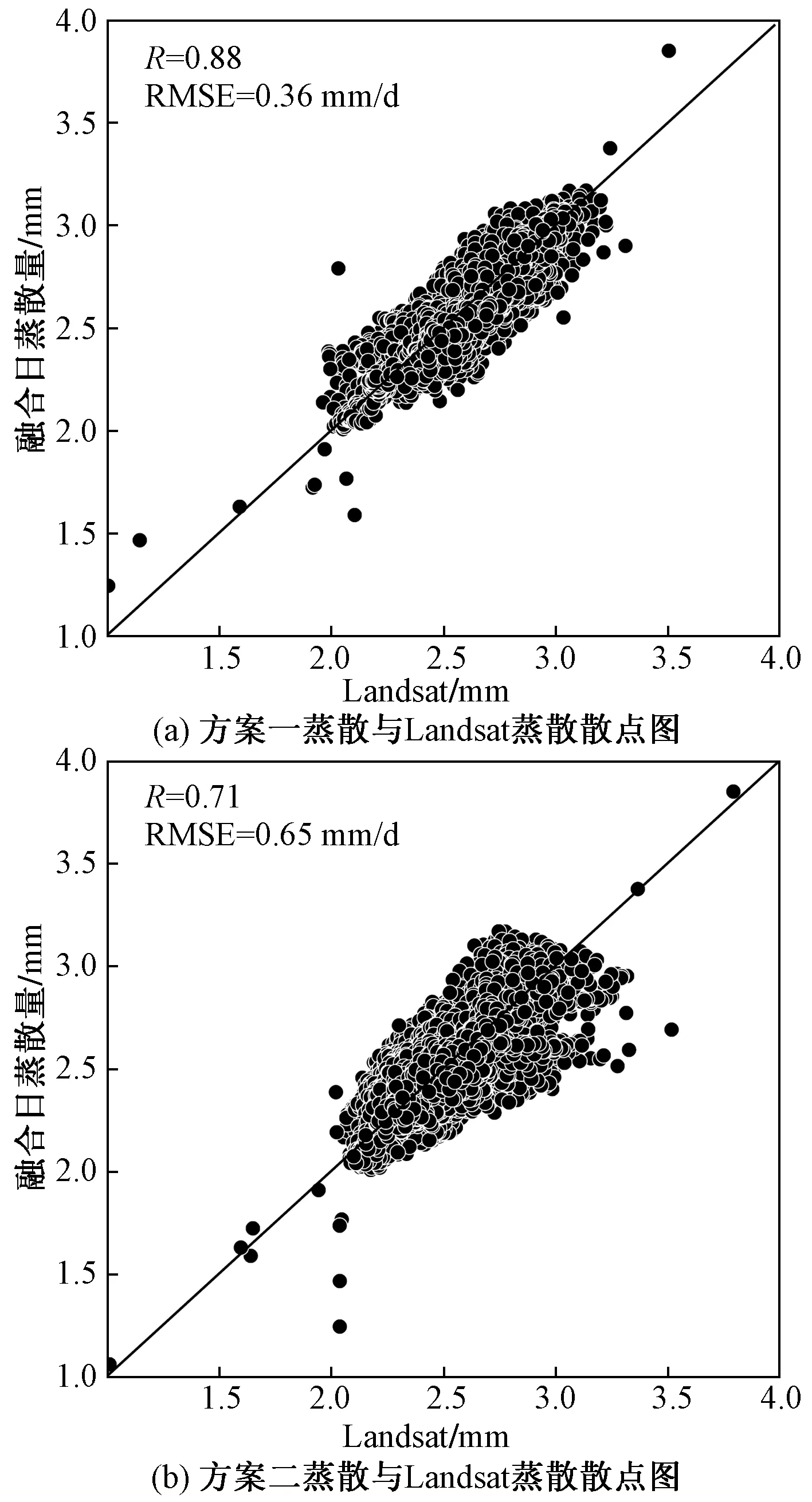
图13 不同方案的融合蒸散与Landsat蒸散相关性分析Fig.13 Correlation analysis between fusion evapotranspiration of different schemes and Landsat evapotranspiration

5 结论

将ESTARFM时空融合算法与SEBS模型相结合计算黄河三角洲地区的蒸散量,获得了研究区不同土地利用类型的高精度蒸散结果,并利用参考蒸散量、通量站和蒸发皿数据等对蒸散结果进行了验证,研究结果如下。

(1)ESTARFM算法能够解决单一传感器限制和云雨污染的问题,不仅可以提高影像的时空分辨率,还有着较高的光谱还原度。融合反射率与实际反射率的相关系数R均在0.85以上,均方根误差RMSE接近于0。但融合效果对输入影像的质量要求较高,输入影像的质量越高、光谱差异越小,融合精度越高。

(2)融合模型和蒸散模型的结合方式对蒸散的计算结果具有一定影响,先融合数据后计算蒸散的方法得到的蒸散结果精度更高,更适用于黄河三角洲地区的蒸散研究。融合日蒸散量与参考蒸散量的变化趋势高度一致,二者相关系数R达到了0.87。模型计算的农田瞬时显热通量与通量站观测的显热通量的相关系数R达到了0.87,均方根误差RMSE为57.8 W/m2。融合数据计算的水面蒸发与蒸发皿折算数据的相关系数R达到了0.93,均方根误差RMSE仅为0.35 mm/d。基于融合数据的蒸散结果在保证蒸散精度的同时,有效提高了蒸散的时空分辨率,能够满足地表破碎地区的蒸散研究需求。

(3)黄河三角洲蒸散量随季节变化较大,夏季蒸散量较高,约占全年的40%。受土地利用和植被覆盖的影响,研究区蒸散量空间变异性较大,高值主要分布在沿海滩涂和内陆水体等区域,低值集中内陆居民区和西南部的裸地等植被覆盖率较低区域。蒸散量在不同土地利用类型中具有明显的差异性,水体、滩涂等自然地物的蒸散量明显高于农田、建设用地等人工地物。

基于ESTARFM算法和SEBS模型能够有效提升蒸散数据的时空分辨率,但是融合算法对输入影像的质量要求较高,应尽可能选择时间间隔较短的输入影像以最小化地表突变所引起的反射率差异。研究区地表破碎化程度高,混合像元较多,这会对融合精度产生一定影响,后续应对时空融合算法进一步优化,提升融合精度并尝试多种传感器数据的融合,以构建长时间连续的高分辨率蒸散序列。