基于特征模式分解的水声目标特征提取方法

李紫鹏, 纪永强, 郭兵勇, 杨坤德

(1.西北工业大学 航海学院, 陕西 西安 710072; 2.中国船舶集团有限公司 系统工程研究院, 北京 100094; 3.西北工业大学 海洋研究院, 江苏 苏州 215400)

水声目标检测与识别是水声探测领域的关键技术,也是水声信号处理中的重点和难点[1-2],从辐射噪声信号中提取目标特征是其中最常用也是最有效的方法之一[3]。

但在现实环境中所获取到的辐射噪声信号往往会受到复杂海洋环境的影响,导致信号具有强非平稳性和极低信噪比[4]。这种情况下,从原始辐射噪声信号中直接提取目标特征几乎是不可能的。在这种情况下,基于小波变换(wavelet transform, WT)[5]、经验模式分解(empirical mode decomposition, EMD)[6]、变分模式分解(variational mode decomposition, VMD)[7]等先进信号分析技术被广泛应用于辐射噪声信号的分析与处理中。

基于WT的信号处理方法,例如离散小波、连续小波、双树复小波、多小波等,最先被应用于水声信号处理中,并取得了较好的结果。但是小波变换的核心缺点在于其固定的基函数只能应对单一的水声目标特征[8],尽管国内外学者通过构造包含多个小波基函数的基函数族满足不同水声目标特征的提取需求,但是固定的基函数仍限制了小波方法的发展。不同于使用固定基函数的傅里叶变换与小波变换,基于EMD和VMD的方法给出了自适应的特征提取思路,并在水声信号处理领域得到了最为广泛的应用。然而,EMD方法的性能受制于端点效应和局部极值搜索算法的影响,且作为一种递归方法,每一次模式分解的误差都会向下累积,最终导致分解失真[9];而VMD方法的性能则受制于分解参数的选取,在实际水声目标识别中无法准确定义相关分解参数(模式数目与带宽),从而降低了VMD分解的准确性与可靠性[10]。因此,研究者们希望寻求一种更为有效的、自组织的、非递归的自适应水声信号特征提取方法。

受经验模式分解、变分模式分解等方法的启发,苗永浩[11]提出了一种全新的时间序列信号自适应分解方法,即特征模式分解(feature mode decomposition, FMD),并将其应用于旋转机械的故障诊断中,取得了较好的特征提取效果与运算效率。

本文提出一种参数优化的特征模式分解方法,通过相关峭度对特征模式分解中的参数进行优化以实现最优分解,并根据模式之间的相似性进行模式融合,以提高微弱特征在信号中的表征,从而实现复杂水声环境下的微弱目标特征提取。

1 参数优化的特征模式分解算法

1.1 特征模式分解

受经验模式分解的启发,特征模式分解也是一种非递归的信号分解方法,它通过设计最优FIR滤波器组,将原始信号自适应地分解为不同的模式。在寻找最优滤波器组与分解结果的过程中,特征模式分解迭代更新滤波器系数,并趋向于使子信号的相关峭度最大。因此,模式分解算法可以被视为求解约束下的最优化问题,即:

(1)

式中:C表示相关峭度(correlative kurtosis,CK),反映模式的脉冲性和周期性[12];uk表示第k个模式;fk(l)表示第k个滤波器,其窗长为L;Ts是估计的特征周期。

采用迭代特征值分解算法求解公式,首先将公式(1)表示为矩阵形式:

(2)

模式的相关峭度则可以表示为:

(3)

式中WM是加权相关矩阵的中间变量:

(4)

结合式(1)、(2)、(4),可以得到FMD目标函数的最终表达:

(5)

式中RXWX和RXX分别是加权相关矩阵和相关矩阵。至此,第k个滤波器的系数可以根据式(5)进行更新,并且可以通过优化的FIR滤波器组来获得单分量模式。

考虑到多调制现象,分解得到的单分量模式可能包含相同的目标特征,并且其中一些模式是无意义的噪声分量。为了消除冗余模式并减少计算量,FMD设计了一种迭代算法:在每次分解之后,首先选择具有最大相似性的2个模式,并从这2个模式中剔除CK较小的模式;其次,通过剩余的模式来重构新的输入并进行FMD分解;直到残差信号满足终止条件,对最终保留下的模式进行解调分析,其过程如图1所示。

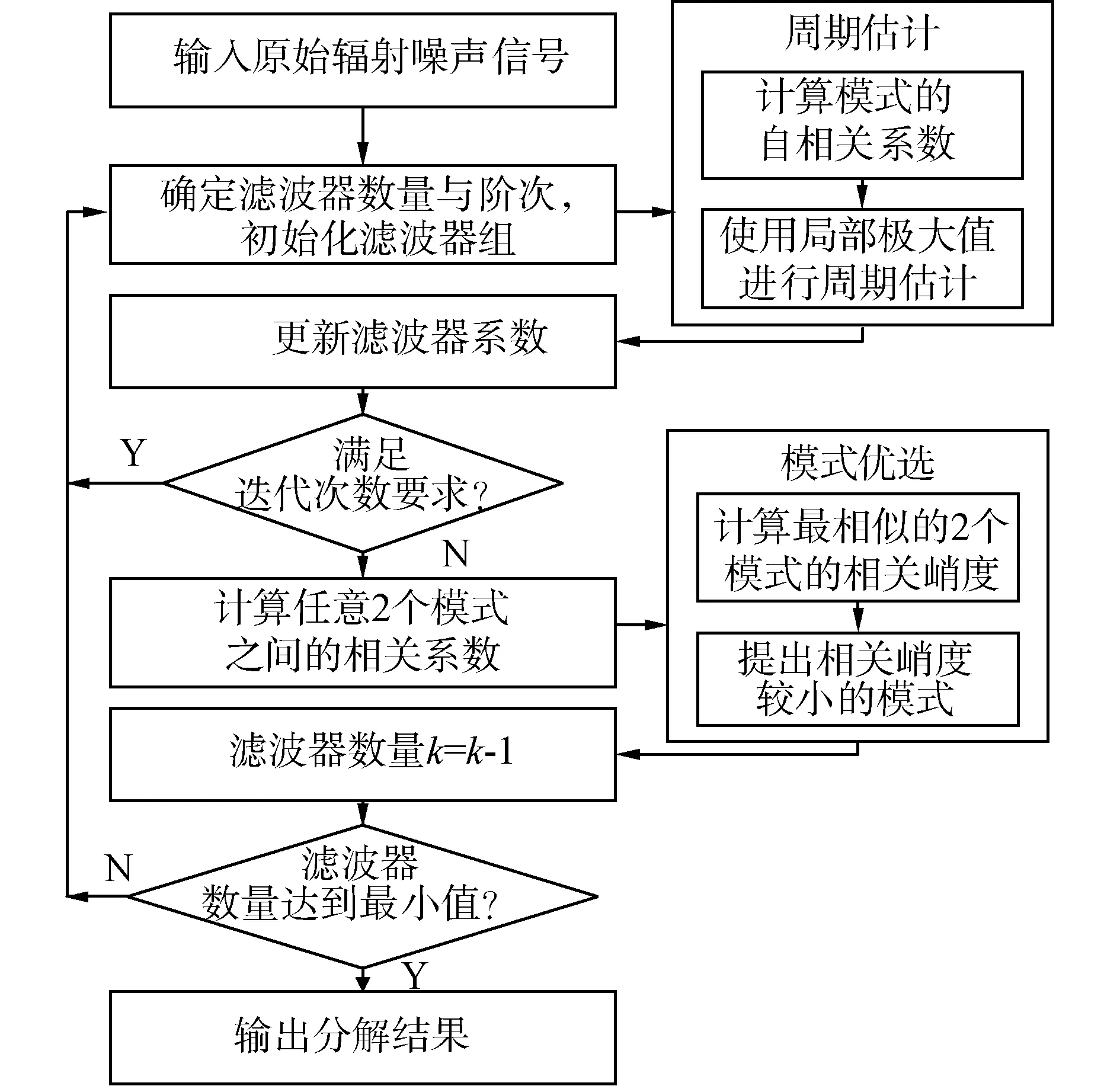
图1 特征模式分解算法流程

1.2 参数优化的特征模式分解

1.2.1 滤波器数量与阶次优化

基于包络信号获得的峭度指标可以很好地表征目标特性,因此可以作为滤波器数量与阶次的优化目标:首先,将滤波器组阶次设置为默认值,并使用模式的包络谱峭度来优化和确定滤波器数量。然后,基于优化的滤波器数量(固定值),使用包络谱峭度优化滤波器组阶次。最后使用优化后的参数对原始信号进行FMD分解。具体过程如下。

1)固定滤波器组阶次为30,滤波器数量的搜索范围固定为M∈[2,15],针对每一个滤波器数量Mi,对原始信号进行FMD分解,获得Mi个模式,并对这Mi个模式进行包络分析获取其包络谱;

(6)

(7)

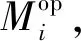
(8)

4)固定滤波器数量Mi,滤波器数量的搜索范围固定为N∈[20,50],针对每一个滤波器数量Ni,对原始信号进行FMD分解,获得Ni个模式,并对这Ni个模式进行包络分析获取其包络谱;

1.2.2 模式融合与优选

考虑到原始FMD算法实际上剔除较多了包含相似目标特征的模式,因此在获取最有分解参数后,仅对原始信号进行一次FMD分解以获得单组分模式,不再进行相似模式筛除、信号重构、再分解等步骤。

获得若干单组分模式后,分别计算这些模式的包络谱之间的皮尔逊相关系数[14-15]：

(9)

1)子信号必须包含相关峭度最大的模式;

2)如果有多个子信号满足条件(1),则从中选取由最多模式融合得到的子信号。

1.2.3 模式融合与优选

完整参数优化的特征模式分解算法流程,如图2所示。

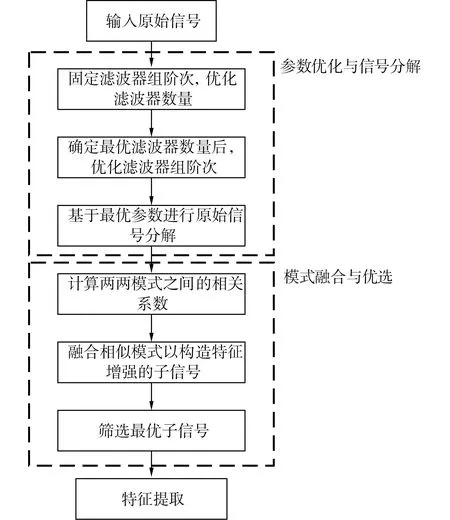
图2 参数优化的特征模式分解算法流程

2 目标特征提取方法仿真分析

在仿真信号中,假设辐射噪声信号是由若干调幅调频信号与高斯白噪声混合而来[16]：

x(t)=∑iAie-2πfiβ(t-ti)cos(2πfi(t-ti))+n(t)

(10)

式中:Ai为振幅;β为振动特征的衰减特性;n(t)为噪声。特征频率设置为10 Hz。测试信号的采样率为5 000 Hz,采样时长为1 s。仿真信号如图3(a)所示。加噪后的仿真信号信噪比为-15 dB,噪声信号如图3(b)所示。噪声信号的频谱和包络频谱如图所示。分别为图3(c)和图3(d)。

从图3(d)中可以看出,由于强噪声的干扰,信号的包络谱中仅出现了一个频率为10 Hz谱峰,且强度较低,无法判定10 Hz就是目标的特征频率。

因此利用本文提出的方法对加噪后的仿真信号进行处理,先设置滤波器组阶次为30,当滤波器数量M为13时,模式包络谱的峭度取得最大值,为3.23;然后固定滤波器数量N为13,当滤波器数量阶次N为41时,模式包络谱的峭度取得最大值,为3.46。根据上述获得的最优参数对仿真信号进行分解,获得13个模式。

然后计算这13个模式两两之间的相关系数,选取大于0.65的模式进行合并,获得的子信号如表1所示,其中模式3为CK最大的模式,因此只考虑包含模式3的子信号。

表1 模式合并后的子信号

根据子信号的筛选规则,选择子信号7进行希尔伯特解调分析,结果如图4所示。可以看出,图中目标特征10 Hz及其高阶谐波均十分明显,且频谱中的地毯值被控制在了极低的水平,说明参数优化的FMD方法能够有效提取并增强噪声信号中的微弱特征。

为进一步评估所提出方法的有效性,将本文所提出方法与EEMD、VMD和固定参数的FMD方法进行比较,将原加噪冲击信号分别进行EEMD、VMD和固定参数的FMD分解,其中EEMD选用的白噪声标准差为0.2,混淆噪声分解的迭代次数为50次,即取仿真信号进行50加噪与EMD分解,将获得模态的平均值作为最终分解结果;VMD分解中模式数目K和带宽α分别5和2 000,即将原始仿真信号分解为5个带宽为2 000的模式,且这些模式能够最大程度上重构原始信号;FMD中的滤波器数目和滤波器组阶次分别取5和30。然后以最大峭度为依据选取敏感模式进行包络谱分析,结果如图5所示。

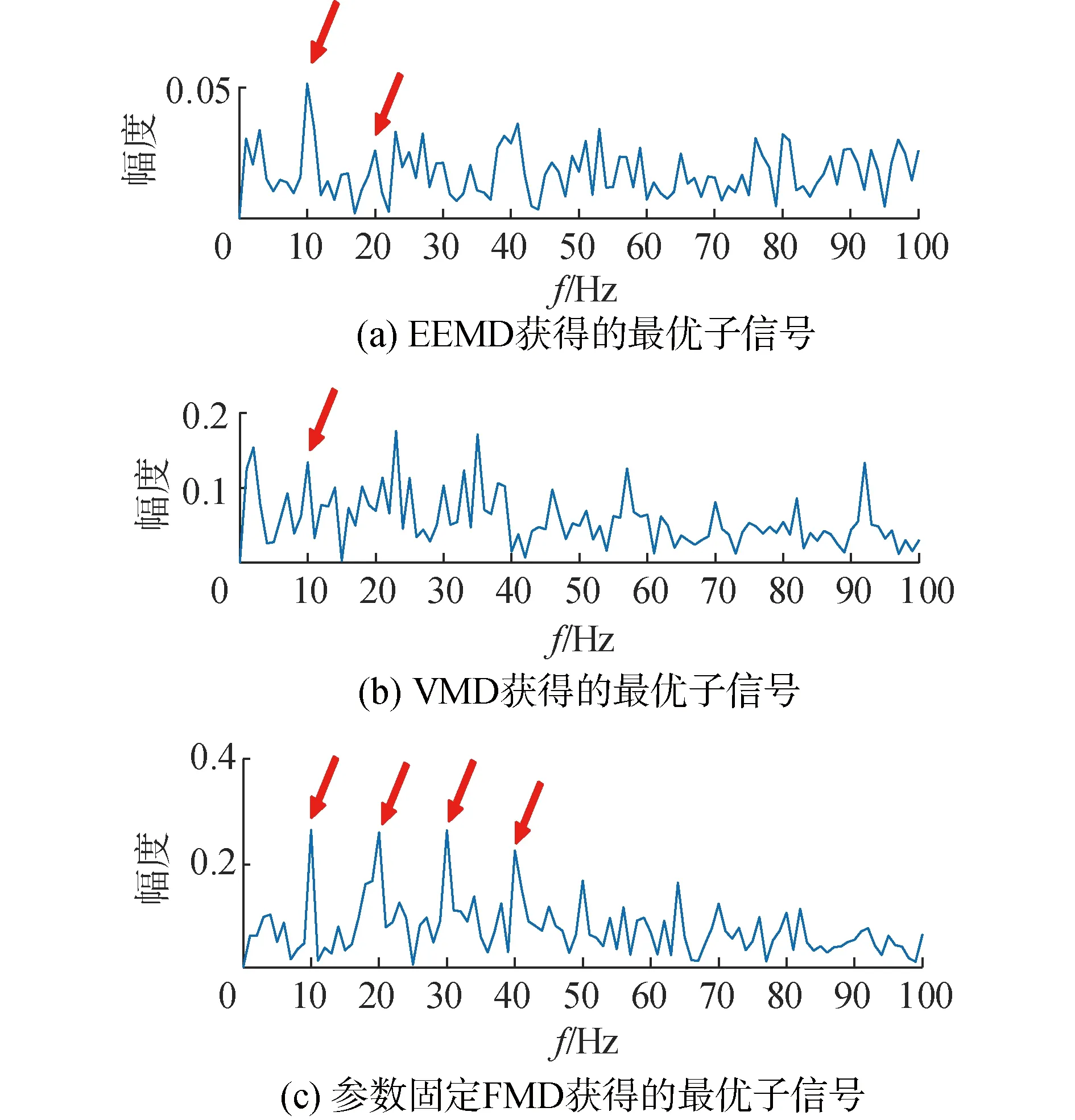
图5 最优子信号的包络谱

EEMD、VMD和固定参数的FMD均能够在不同程度上识别出特征分量,但是3种方法特征频率与本文方法相比不明显,且均无法识别更高次的谐波分量。其中EEMD方法的效果最差,其在于EEMD方法的前几个宽带模式包含了大量噪声组分;VMD和固定参数的FMD方法中存在大量无意义的干扰,这些干扰的幅值甚至大于目标特征频率。因此,本文方法在微弱特征提取及表达方面具有更好的效果。为了进一步验证该方法的有效性和工程应用价值,下一节将采用该方法对真实海试数据进行分析。

3 实验验证与分析

课题组于南海某处设计并开展了一次水声目标辐射噪声信号探测和采集实验。带有3个水听器的测量船和目标船如图6所示。测量船的发动机熄火,目标船以匀速航行。在本次实验中共获得了61组辐射噪声信号,这些信号的采频为20 kHz,大多数辐射噪声信号可以很容易地进行分析,所包含的船舶轴系特征频率也很明显。

图6 水声目标辐射噪声信号探测和采集实验

为了验证本文所提出方法的有效性,仍然采用参数优化的FMD方法、EEMD、VMD和固定参数的FMD4种方法分别处理所有的辐射噪声信号。每种方法的性能如表2所示。

表2 不同信号分解方法的目标特征提取能力

随后,选取一条目标特征微弱的辐射噪声信号进行分析。首先对其进行降采样,将采样频率降至5 000 Hz。降采样后的信号时域波形如图7(a)所示,其频谱和包络谱分别如图7(b)和7(c)所示。图7(a)中无明显的周期性震荡,图7(b)和7(c)中也无显著的特征谱线。

图7 实测辐射噪声信号时域波形、频谱及包络谱

使用本文提出的参数优化FMD对原始信号进行处理,当滤波器数量M为10时,模式包络谱的峭度取得最大值,为3.78;然后固定滤波器数量N为10,当滤波器数量阶次N为37时,模式包络谱的峭度取得最大值,为4.59。根据上述获得的最优参数对仿真信号进行分解,获得10个模式。

然后计算这10个模式两两之间的相关系数,选取大于0.65的模式进行合并,其中模式6为相关峭度(CK)最大的模式,因此只考虑包含模式6的子信号,即由模式3、6、7构造的子信号是最优子信号。对其进行包络解调,其结果如图8所示。

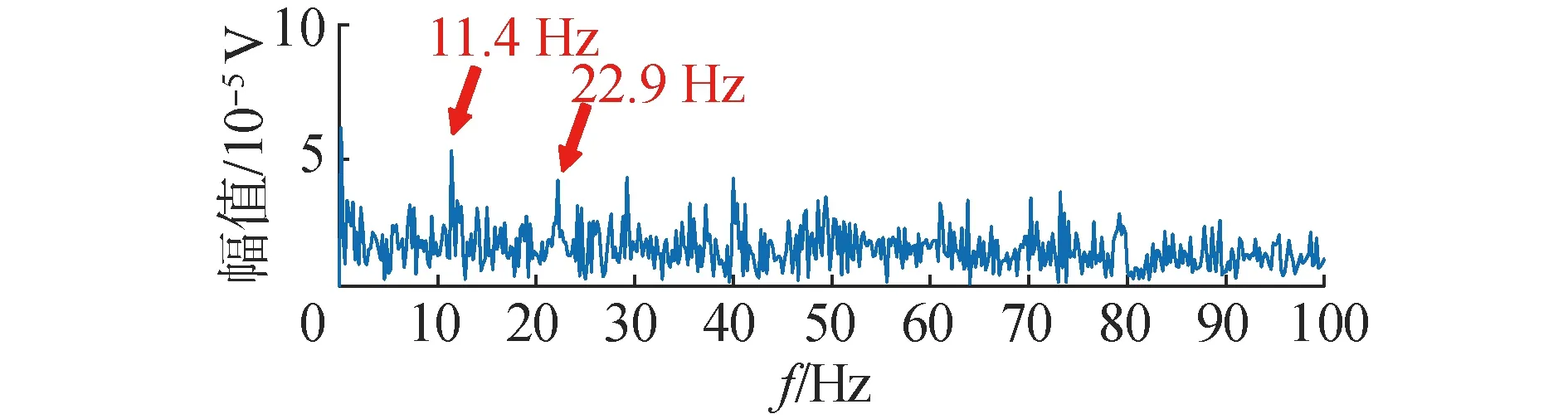
图8 最优子信号的包络谱

图8中有较为明显的目标轴系特征频率及其2倍频,作为谱线特征进行目标的检测与识别。同样地,将该方法与EEMD、VMD和固定参数的FMD方法进行比较,其中EEMD的噪声标准差为0.2,分解次数为50;VMD分解中模式数目K和带宽α分别8和2 000;FMD中的滤波器数目和滤波器组阶次分别取7和25。然后以最大峭度为依据选取敏感模式进行包络谱分析,结果如图9所示。

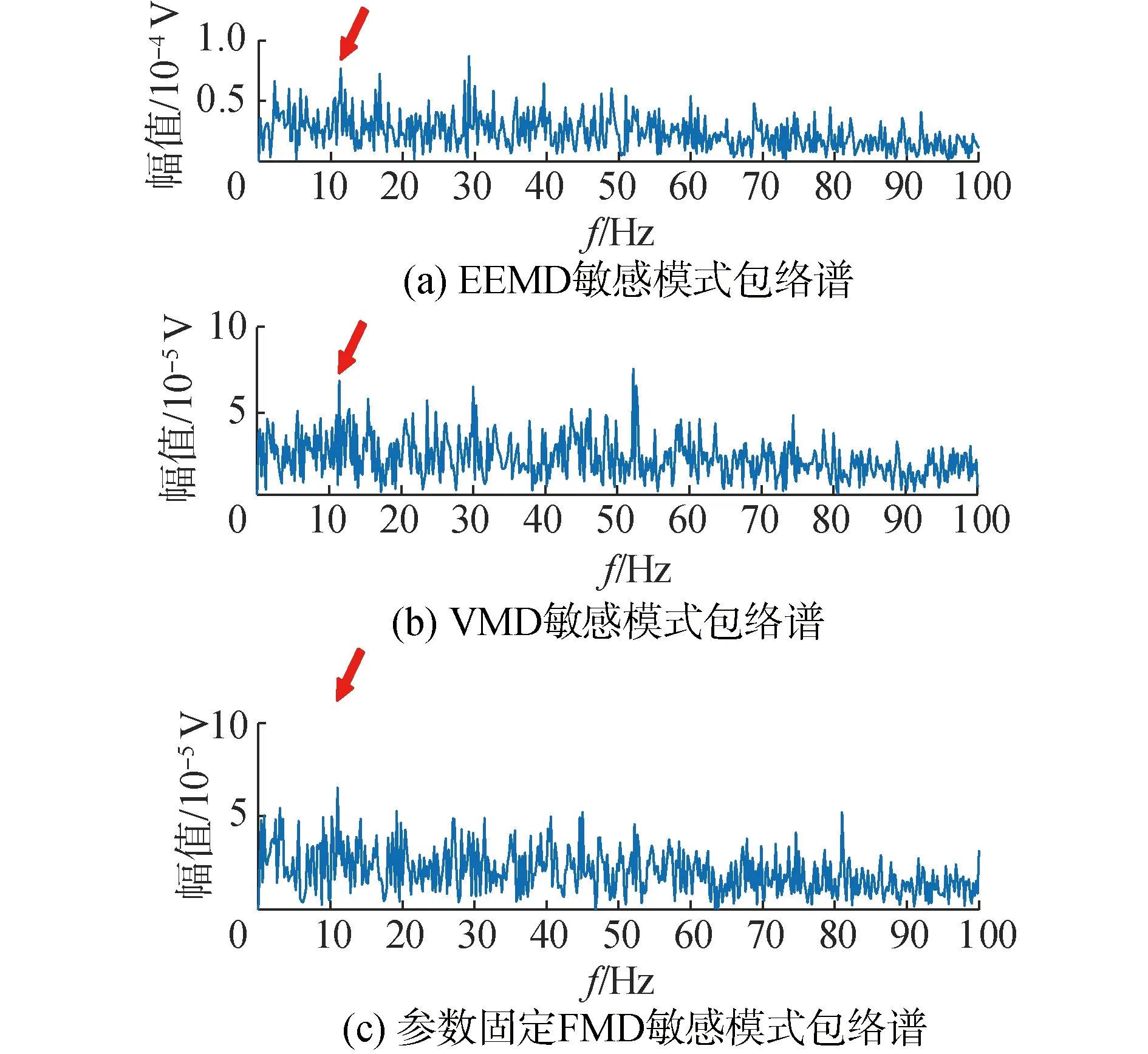
图9 3种方法的最优子信号包络谱

从图9中可以看出,EEMD仅能提取出目标轴系特征频率,且幅值较低,谱线不明显;VMD方法可以提取出目标轴系特征频率及其二倍频,但是谱线不突出,且地毯值较高;固定参数的FMD也仅能提取出目标轴系特征频率,且极为模糊。因此,进一步验证了本文方法在水声目标特征提取方面比EEMD、VMD和固定参数的FMD方法具有更好的效果。

4 结论

1) 本文将FMD这一自适应信号分解方法应用到水声目标检测与识别领域,并克服了FMD的参数选择问题,能够自适应地获取与待分解信号相匹配的滤波器数目M和滤波器组阶次N。

2) 引入基于相似理论的模式融合方法,增强了微弱目标特征的表达,同时给出了融合后的子信号优选准则,降低了算法的计算复杂度。

3) 采用该方法分别对仿真和实验信号进行分析,均成功识别出信号中隐藏的微弱目标特征。通过与EEMD、VMD和固定参数的FMD方法的比较,进一步验证了该方法在水声目标特征提取方面的优势。

该方法对水声目标的检测与识别具有一定的工程应用价值,在满足辐射噪声采集、存储及算法运行时间要求的前提下,该方法可用于水声目标的在线检测与识别。下一步将针对该方法的适用范围进行研究,以确定该方法在不同强度、不同信噪比的辐射噪声下的适用性。