传递误差对行星齿轮动态特性的影响

鲁文佳，朱丽莎

（肇庆学院机械与汽车工程学院，广东 肇庆 526061）

前 言

行星齿轮系统因其紧凑的结构形式和大传动比，使之成为变速箱中十分常用且重要的变速装置.国内外学者针对行星齿轮传动系统展开了相关研究.Cao 等[1]通过研究行星齿轮偏心距对系统时变啮合刚度的影响，建立了考虑齿轮偏心制造误差下的行星齿轮系统动力学模型.Mo等[2]考虑了行星齿轮系统啮合齿隙变化引起的浮动啮合误差，建立了考虑位移相容性的两级外啮合行星传动系统齿轮的多体负荷分配模型，并考虑了浮动轨道的变化规律和中心轮的浮动量.Zhai等[3]考虑到行星系统的装配误差，采用集总参数法建立了风力发电机齿轮箱螺旋行星齿轮系统的弯扭耦合振动模型并研究了载体水平装配误差，载体轴装配误差和载体空间装配误差对动态特性的影响.Iglesias 等[4]讨论了制造误差（如偏心距和行星销定位误差）对三级行星传动的准静态特性的影响，揭示了压力角变化时行星的径向定位误差的影响，指出径向定位误差在某些操作条件下对载荷分配比具有不可忽略的影响.Sheng等[5]提出了一种具有齿轮间隙和轴承间隙的行星齿轮组非线性横向扭转耦合模型，分析了太阳轮的支承刚度和偏心误差，行星的偏心误差等对系统动态负载分担特性的影响.CHEN和QIU[6-7]等将时变啮合刚度以参数激励的方式作用于行星齿轮系统，分别研究了齿轮轴向倾翻和啮合相位对行星齿轮系统接触特性和动态特性的影响以及时变啮合刚度和齿轮速度波动对系统响应的影响.BAI和YANG[8-9]等均建立了机电行星齿轮系统耦合动力学模型，研究了电压瞬变对机电系统动态特性的影响和电磁效应对行星齿轮箱固有振动特性的影响.YANG和LIU[10-11]均研究在不同载荷条件下，行星齿轮系统误差对载荷分配行为的影响以及考虑静态传递误差下的强迫振动响应.Hammami等[12]考虑时间变化的负载条件和齿轮啮合的接触的非线性，利用有限元法和赫兹接触理论对齿轮啮合刚度进行建模，开发了具有动力再循环的行星齿轮的扭转集总参数模型.关于齿轮系统中啮合刚度的研究，CHAARI、MA和王奇斌[13-15]等基于能量法建立了齿轮的时变啮合刚度模型，其中王奇斌[15]基于齿轮啮合刚度模型考虑传递误差来源，对齿轮传递误差进行了研究.

现有关于行星齿轮的研究或研究偏心误差，或制造误差，或装配误差等某个方面对行星系统的影响，很少系统揭示综合传递误差对行星齿轮动态性能的影响，因此难以具有通用性.本研究拟建立通用性更强的考虑误差因素的行星齿轮动力学模型，以载荷激励的方式建立传递误差内激励数学模型，适用于行星多自由度系统并能深入解析内外部激励源对行星齿轮系统产生的不同影响.

1 考虑误差因素的行星齿轮动力学模型

考虑行星齿轮系统误差建立系统的振动参数化模型如图1 所示.分别建立OXY固定坐标系和Onζnηn随动坐标系.坐标系OXY的原点为太阳轮质点中心位置O，X轴为O点和第一个行星轮质点中心o1的连线；坐标系Onζnηn与行星架固联并以相同角速度(ωc)转动，原点on位于第n个行星轮的质心，坐标轴ζn通过on与O所在直线.下角标c，r，s分别代表行星架，内齿圈和太阳轮.n(n=1,2,...,N)表示第n个行星轮，N代表行星轮的个数.该模型将行星系统不同零部件简化成相应的质点，通过系统的位置参数表示系统各部件的相对位置关系.分别考虑平面内X，Y方向的移动自由度和绕平面的转动自由度，从而建立系统的动力学微分方程.

图1 行星齿轮系统动力学模型简化图

对于太阳轮有：

其中：ms和Is分别代表太阳轮的质量和转动惯量.rs代表太阳轮的基圆半径；ksu代表太阳轮与各行星轮之间的啮合刚度；ksx和ksy代表太阳轮的径向支承刚度；ksu代表太阳轮的扭转支承刚度；δsn为太阳轮与第n个行星轮在啮合线方向上的弹性变形.

式中：αs为太阳轮与行星轮之间的啮合角(ψsn=ψn-αs)，ψn为第n个行星轮的位置角，；esn为太阳轮与行星轮的传递误差.

对于内齿圈有：

其中：mr和Ir分别代表内齿圈的质量和转动惯量.rr代表内齿圈的基圆半径；krn代表内齿圈与各行星轮之间的啮合刚度；krx和kry代表内齿圈的径向支承刚度；kru代表内齿圈的扭转支承刚度；δrn为内齿圈与第n个行星轮在啮合线方向上的弹性变形.

式中：αr为内齿圈与行星轮之间的啮合角(ψrn=ψn-αr)；ern为内齿圈与行星轮的传递误差.

对于行星架有：

其中，mc和Ic分别代表行星架的质量和转动惯量；rr代表行星架的当量基圆半径；kpn代表各行星轮的支承刚度；kc代表行星架的径向支承刚度；kcu代表行星架的扭转支承刚度；δζn，δηn为行星架相对于第n个行星轮在ζ和η方向的投影.

式中：eζn和eηn为行星架相对于第n个行星轮在ζ和η方向的误差，主要包括制造和安装引起的系统误差以及几何偏心引起的误差等.

对于行星轮有：

其中：mn和In分别代表第n个行星轮的质量和转动惯量；rn代表第n个行星轮的基圆半径.

将式(1)-(16)联立可建立矩阵形式的行星系统动力学方程.

式中：M，C，K分别为系统的质量矩阵，阻尼矩阵和刚度矩阵（包括支承刚度和啮合刚度），啮合刚度项采用时变啮合刚度确定，阻尼项采用瑞利阻尼形式来确定[16]；q为系统的广义坐标；F1(t)和F2(t)分别为系统内外激励向量.

由于误差因素引起的系统内激励向量可表示为：

2 系统内外部激励

齿轮传递误差是指从动齿轮真实啮合位置与理论啮合位置的偏差.齿轮传递误差由轮齿的弹性变形和安装制造误差等因素造成，导致轮齿之间发生碰撞和冲击，形成了齿轮啮合的误差激励.齿轮传递误差随着齿轮啮合发生周期性变化，可利用傅里叶级数展开的方式将齿轮传递误差表示为[17]：

式中：e0为轮齿误差均值；eai为误差谐波分量幅值；f为轮齿的啮合频率.

太阳轮和行星轮的传递误差esn、内齿圈和行星轮的传递误差ern均可利用傅里叶级数展开，太阳轮与行星轮的时变啮合刚度fsn和内齿圈与行星轮的时变啮合刚度fsn，可根据文献[15]方法得到，利用式(29)即可得到系统的内部激励，相应的内部激励频率分别为太阳轮与行星轮的啮合频率fs和内齿圈与行星轮的啮合频率fr.行星架相对于行星轮的误差eζn和eηn以行星架的转动频率fc周期性变化，行星架处外载激励同样以其转动速度fc周期性变化，两者相互叠加可等效为系统外激励共同作用于行星架所在节点，相应的外部激励频率为fc.

3 数值计算

以某型采煤机截割部行星齿轮系统作为分析对象，其行星齿轮系统三维模型如图2所示.主要参数值：太阳轮齿数zs=16，内齿圈齿数zr=68，行星轮齿数zn=25，行星轮个数N=4，模数m=9 mm，行星架转速60 r/min，行星架所受等效载荷扭矩TC=1.935×104 N·m.根据文献[15]的方法得到行星齿轮系统的时变啮合刚度如图3所示.

图2 某型采煤机截割部行星齿轮系统三维模型

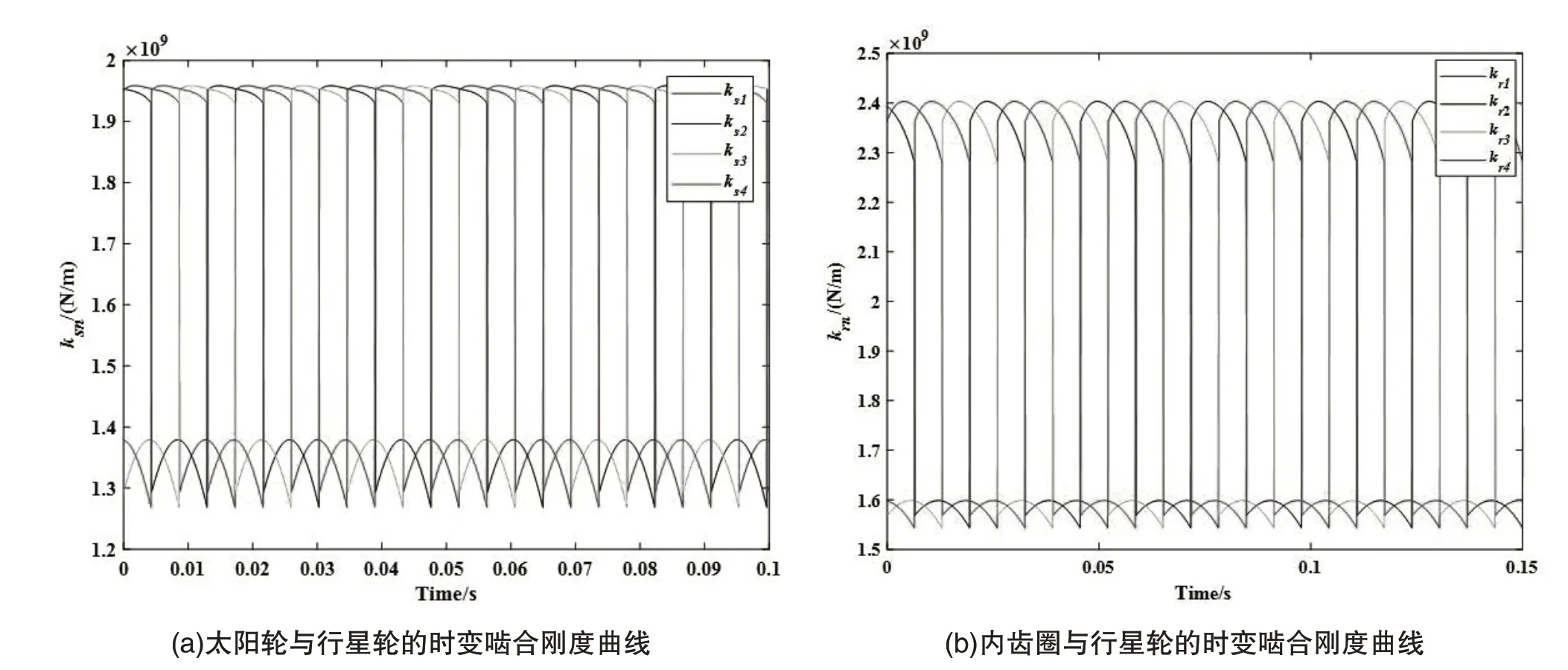
图3 行星齿轮系统的时变啮合刚度

3.1 系统的动态响应与结果分析

分别计算得到了行星齿轮系统在考虑误差因素和不考虑误差因素情况下系统的动态特性.图4为太阳轮分别在考虑误差因素和不考虑误差因素影响的情况下y方向和绕z轴转动方向的位移、速度和加速度的时域响应曲线.图5为行星轮在两种情况下的位移、速度和加速度时域曲线.

图4 太阳轮位移、速度和加速度时域曲线

图5 行星轮的位移、速度和加速度时域曲线

对行星齿轮系统主要部件的位移、速度和加速度时域曲线进行傅里叶变换得到主要响应的频域结果.图6为太阳轮在考虑误差因素影响时y方向的位移、速度和加速度的频域分析图.图7为考虑误差因素影响时太阳轮绕z轴转动方向的位移、速度和加速度的频域图.

图6 太阳轮y方向的位移、速度和加速度频域图

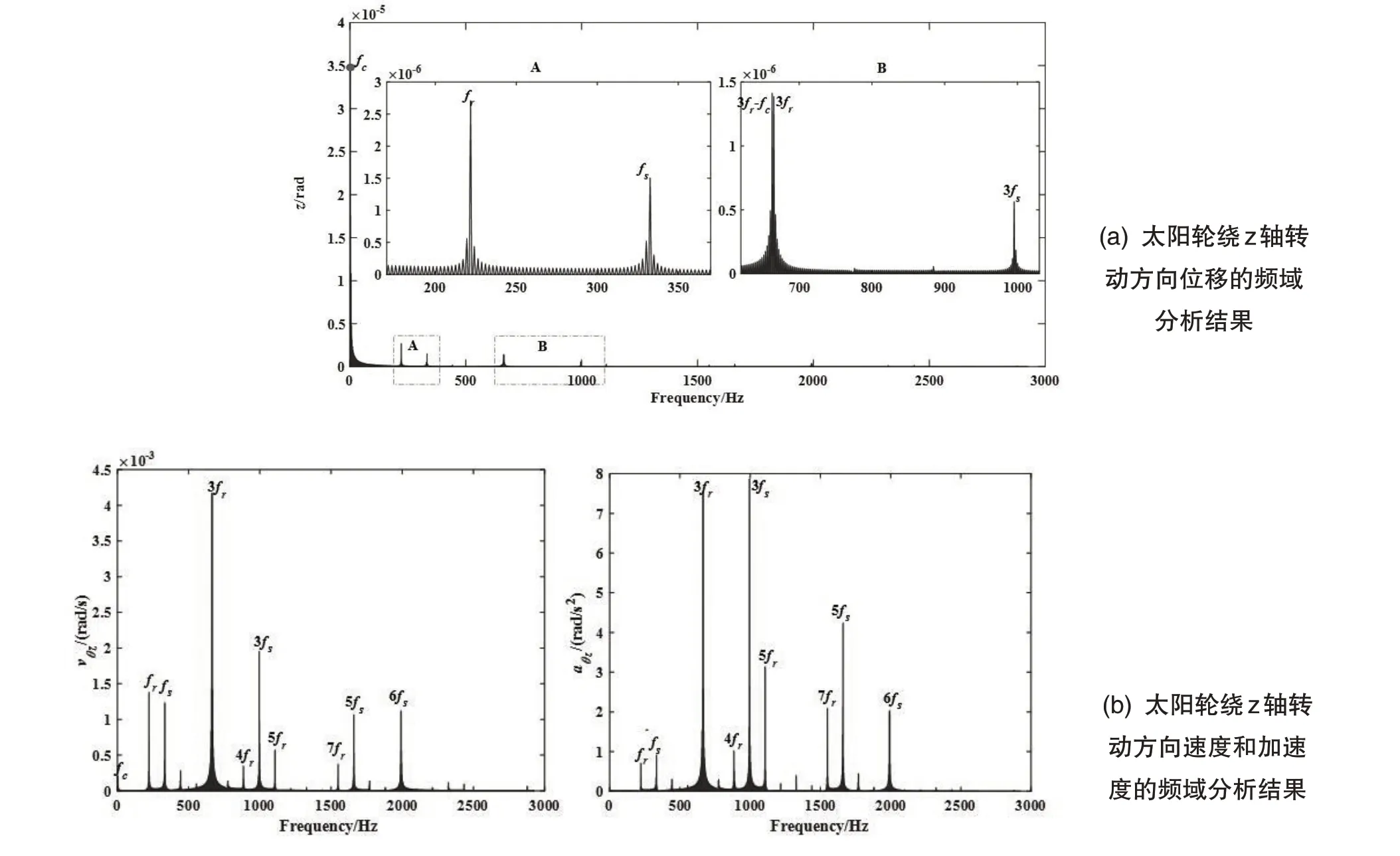
图7 太阳轮绕z轴转动方向的位移、速度和加速度频域图

分析图6、图7太阳轮和行星轮的位移频域图可以发现，由外激励频率fc激发的低频区是行星系统位移产生的主要原因.A区和B区是由内部误差激励频率fs和fr引起的高频区，只存在于考虑误差因素的系统响应中，不考虑误差因素时，其频域结果不存在高频区.因此对于理想的行星系统振动只存在由行星架转轴频率fc激发的低频振动.由图6和图7行星系统的速度和加速度频域结果图可以得出，在考虑误差因素时，啮合频率fr与其倍频3fr，4fr，5fr，7fr和啮合频率fs与其倍频3fs，5fs，6fs是太阳轮和行星轮的主要频率成分，说明行星系统速度和加速度主要由内部激励频率fr、fs以及他们的谐频成分激发产生，考虑系统误差因素引起的内部激励是系统产生速度和加速度的主要原因.

3.2 传递误差对系统动态力的影响

传动系统齿轮副间的动态啮合力为啮合线上轮齿的相对位移与啮合刚度的乘积.图8为分别考虑误差因素与不考虑误差因素，行星齿轮系统中太阳轮和行星轮啮合副的动态啮合力fsn(n=1,2,3,4)的时域分布图，图9为分别考虑误差因素与不考虑误差因素，内齿圈与行星轮啮合副的动态力frn(n=1,2,3,4)的时域分布图.对行星系统动态啮合力fsn和frn进行快速傅里叶变换，得到系统动态力的频域分析图.图10为太阳轮和行星轮的动态啮合力的频域分析图，图11为内齿圈和行星轮的动态啮合力的频域图.

图10 太阳轮和行星轮动态啮合力的频域图

图11 内齿圈和行星轮动态啮合力的频域图

误差因素对行星系统的动态啮合力的影响可由图8和图9非常直观的展现，较理想行星系统其动态载荷呈现明显的频繁波动，这正是由内部动载荷激发产生的.考虑误差因素动态力fs峰值较理想行星系统提高了36.7%，动态力fr峰值较理想行星系统提高了28.5%.当不考虑误差因素影响时，行星系统动态啮合力只在fc附近存在低频区.分析图10和图11系统动态啮合力的频域图，当考虑误差因素影响时，行星系统动态啮合力的频率成分既存在低频区，也存在A，B，C，D等高频区.动态啮合力fs的高频区主要由误差引起的内部激励频率fr和fs、以及他们的倍频3fr和3fs激发产生.同时在这些载波频率周围存在频率成分为(ifs±ifc) (i=1, 3;j=1, 2)和(ifr±jfc) (i=1, 3;j=1, 2)的边频带.动态啮合力fr的高频区主要由误差引起的内部激励频率fr和fs以及他们的倍频3fr和5fs激发产生.同时在以这些内部激励频率作为载波频率的周围存在频率成分为(ifr±jfc) (j=1, 3, 5;j=1, 2 )的边频带.这是由于加载于行星架的外载扭矩以行星架转频为激励频率，形成了以齿轮啮合频率及其谐波为载波频率，行星架转频及其倍频为调制频率的啮合频率调制现象.以上分析得出行星系统的动态啮合力的低频区由行星架转轴频率激发的外载激励产生，理想的行星系统不产生高频成分，误差因素引起的内部激励是系统动态力高频区形成的原因.

误差因素对行星系统的动态啮合力的影响可由图8和图9非常直观的展现，较理想行星系统其动态载荷呈现明显的频繁波动，这正是由内部动载荷激发产生的.考虑误差因素动态力fs峰值较理想行星系统提高了36.7%，动态力fr峰值较理想行星系统提高了28.5%.当不考虑误差因素影响时，行星系统动态啮合力只在fc附近存在低频区.分析图10和图11系统动态啮合力的频域图，当考虑误差因素影响时，行星系统动态啮合力的频率成分既存在低频区，也存在A，B，C，D等高频区.动态啮合力fs的高频区主要由误差引起的内部激励频率fr和fs、以及他们的倍频3fr 和3fs 激发产生.同时在这些载波频率周围存在频率成分为(ifs±jfc) (i=1,3;j=1, 2)和(ifr±jfc) (i=1,3;j=1, 2)的边频带.动态啮合力fr的高频区主要由误差引起的内部激励频率fr和fs、以及他们的倍频3fr和5fs激发产生.同时在以这些内部激励频率作为载波频率的周围存在频率成分为(ifr±jfc) (i=1, 3, 5;j=1, 2 )的边频带.这是由于加载于行星架的外载扭矩以行星架转频为激励频率，形成了以齿轮啮合频率及其谐波为载波频率，行星架转频及其倍频为调制频率的啮合频率调制现象.以上分析得出行星系统的动态啮合力的低频区由行星架转轴频率激发的外载激励产生，理想的行星系统不产生高频成分，误差因素引起的内部激励是系统动态力高频区形成的原因.

4 结论

利用集中质量参数法建立了考虑系统传递误差因素的行星齿轮系统动力学数学模型，得到了由误差激励产生的行星齿轮系统内部附加动载荷模型，较理想行星系统模型相比可将内部误差引起的内部激励量化处理并应用于系统动态特性研究.

行星架转轴频率激发的外激励频率是行星系统位移响应低频区产生的主要原因.内部误差激励频率主要影响的位移响应的高频区.行星系统速度和加速度主要由内部啮合频率以及他们的谐频成分激发产生，系统误差引起的内部激励是行星系统产生速度和加速度的主要原因.

考虑误差因素太阳轮、内齿圈和行星轮的动态力峰值较理想行星系统分别提高了36.7%和28.5%.行星系统的动态啮合力的低频区由行星架转轴频率激发的外载激励产生；理想的行星系统不产生高频成分，误差因素引起的内部激励是系统动态力高频区形成的原因.