数形结合 助推数学思维高阶发展
林燕青
(闽清县白樟镇白南小学,福建 闽清 350804)
《义务教育数学课程标准(2022年版)》的实施,标志着义务教育数学课程改革又一个新阶段的开始。[1]许多新的教学理念对原有的一些教学思想有了很大的冲击。面对课程改革的新浪潮,对于一线教师而言,不管教学的方式方法如何变化,教学始终都是以学生知识的学习和技能的形成为目的,培养学生的思维则是完成这个目的的重要手段之一。围绕数学课程性质中这个明确的育人价值,培养学生的思维,“为思维发展而教” 依然是一线教师在数学教学中努力的方向。[2]理解数学本质、相互关系以及内在规律是数学思维的反映,思维是一种内隐的心理活动,它是看不见、摸不着,抓不住的。[3]在教学中,借助数形结合这种非常重要的数学思想,能有效地将相关信息输入大脑,经思维加工,输出更多的高质量信息,实现思维的可视化。这既是数学思维的价值所在,也是数学教育的目标追求。[4]
数形结合可以将原本比较复杂的数学知识通过更简单的形式呈现,依据数与形的两个特点——精确性与直观性,把运算教学、数量关系等与点、线、面几何直观图形结合起来,使学生思维从具体形象向抽象思维过渡,使两者优势互补、各展所长。利用数形结合,不但能使枯燥的算理形象化,轻松掌握算理,达到准确计算,并灵活应用算理,提高计算能力的目的,还能将抽象的数量直观化,从而拓展学生解决问题的思维,探究数学的内在联系;同时又能通过图形掌握其内在的数学信息,培养学生的空间观念,提升学生的数学素养。
一、以形解数,借算理促形象思维的发展
在数学计算教学中,很多孩子知其然而不知其所以然,对于各种计算题都会算,但是很多孩子被问到为什么这么算,十分茫然,因此,进行计算教学时对算理的教学就显得尤为重要。在教学算理时,为了让学生阐明数与数之间的关系,教师可以借助直观的点子图,以形助数,帮助学生掌握计算方法;以形解数,帮助学生理解算理,让学生的思维逐步清晰,明白其中的道理,从而实现目标的达成。
例如:在教学人教版三年级下册《两位数乘两位数》这节课时,教师引导学生经过阅读和理解例题后,学生很快列出算式:14×12,教师追问:你是怎样计算的呢?为了让学生正确去理解算理理清算法,教师出示点子图,让学生们试着画一画,再算一算,在小组内交流自己的想法。在经过认真的探讨后,学生生成了很多的解答方法:
方法一:14×10=140 14×2=28 140+28=168
方法二:10×12=120 4×12=48 120+48=168
方法三:14×9=126 14×3=42 126+42=168
方法四:14×6=84 84×2=168
方法五:4×2=8 10×2=20 10×4=40
10×10=100 100+40+20+8=168
在汇报的过程中,每组学生都用点子图具体解释了解题思路。学生尝试列竖式,在相互交流后展示了竖式:

14×122814168
师紧接着追问:这里28表示的是什么?14表示的又是什么?你能不能结合点子图来说一说?经过再次的探究和不断地完善,师生很快得出:

2套书的本数←10套书的本数←
进而明确:28指的是2套书的本数,表示2个14,所以28的8要和个位对齐;14实际上是140,是10套书的本数,表示10个14,因为我们在写竖式时把140十位上的4和十位对齐,所以个位上的0可以省略不写。 (见图1)两相对比,先用形的直观阐述数的生成,再用数的简洁来总结出计算的算理。这样的教学,是根据学生的思维特点,利用大量的 “形”来探究计算形成的思路,理解算理、提炼算法,不但降低了学习难度,还拓展了学生的思维,养成学生多角度思考问题的习惯,提高了课堂教学效率。
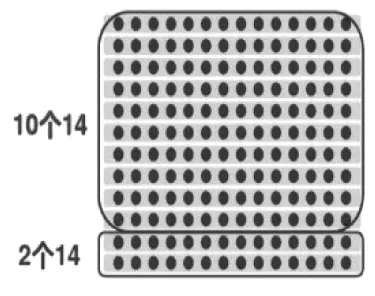
图1
二 、数形结合,借问题促抽象思维的发展
在小学课堂教学中要想让教学活动灵活多样,事半功倍,有的放矢地帮助学生多角度提出问题和解决问题,让学生学会主动有序地去学习,对数学思想的渗透就必不可少。数形结合思想的应用和探究就是需要渗透的数学思想之一。数形结合在小学数学课堂教学中不仅是一个有效的数学思想,也是一种很好的学习方法,更是教师课堂常备的教学手段。他可以把空间形式和数量关系结合起来去分析,感受数与形两者之间的对应关系,并相互转化,从而促进学生形象思维和抽象思维的协调发展,并顺利归纳出解题思路,达到解决问题的目的。
例如:在教学人教版六年级上册《数与形》时,教师出示:(图2)

图2
问:请你仔细观察这一组图形,你能想到哪些数或式子?学生充分利用已有的知识经验发现图形中隐藏的数或式子,并结合图形解释了这些数或式子表示的含义,生成“1=12、1+3=22、1+3+5=32”这些教学资源,教师又问:“按照这样的规律,下一个图形会是什么样?”学生在拼摆中得到:在外围加7个小正方形,这样摆更有规律,更直观地得到1+3+5+7=42。进一步追问:“不摆,要拼一个更大的正方形,能写算式吗?”学生进行思维迁移,不拼就能得出:1+3+5+7+9=52。最后又问:“你能结合图形解释一下为什么要从1开始加起?……”在一连串的追问、反问中,引发学生对数学知识本质的思考,促进学生走向深度学习,不断地让学生感受数与形的联系,也不断地进行数形对照,体会形中有数,数中有形。学生在经历数学抽象概括的过程中,数形结合的方法自然而然地在心中生根发芽。
三 、数形互补,借数量促逻辑思维的发展
数与形两者相比较,“数”比较抽象,“形”则形象直观,两者各有优势。在教学中,若发现学生对有些数量关系难以理解时,可引导学生借助形的形象和直观的两个特点,画出图形或线段,再根据具体的数量帮助理解数量关系,数和图互相补充,相互说明,以图形或线段为思维材料,通过一定的逻辑进行推理,把抽象化的数量关系形象化,让思维可视。解题思路与思考过程一目了然,那么列式解答自然不在话下,数学问题自然也就迎刃而解了。
例如,在教学人教版五年级下册《分数解决问题》时,有一道关于纯牛奶兑水后的题目:“一杯纯牛奶,乐乐喝了半杯后,觉得有些凉,就兑满了热水。他又喝了半杯,就出去玩了,乐乐一共喝了多少杯牛奶,多少杯水?”[5]问题本身并不是很复杂,但是学生在读题时,感觉有点绕口,而题里的数量关系也比较杂乱,既有纯牛奶,又有纯牛奶和水的混合物,学生很难把混合在一起的牛奶和水之间的关系理清楚,更无法解答。这时,教师就可以引导学生用图或线段图把牛奶和水分开,从而简单明了地表示出它们之间的关系:(见图3)
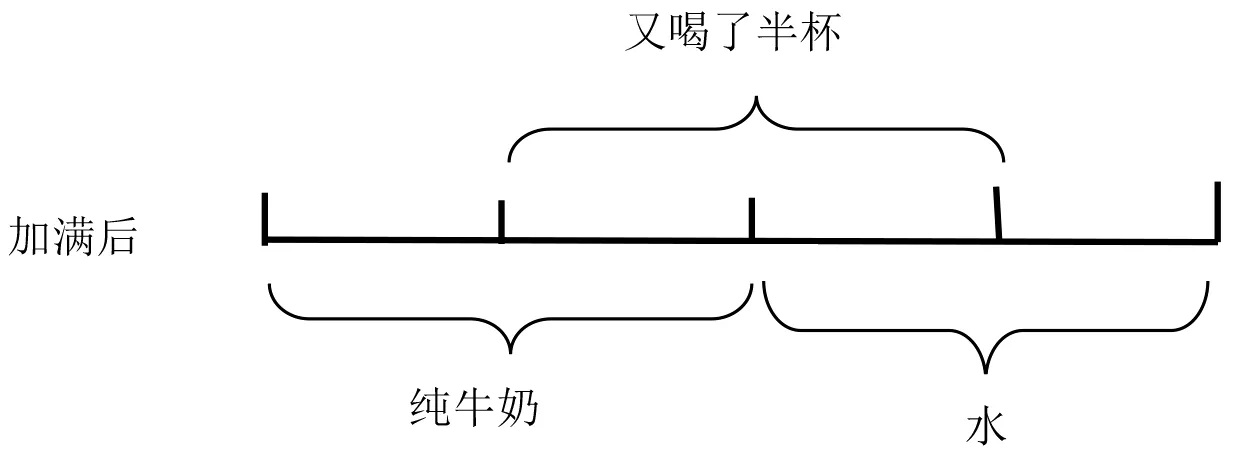
图3

(2)

四、以数辅形,借拓展引领思维进阶
数形结合百般好,隔裂分家万事休。[6]可见,数与形相互依托,联系特别紧密。教师在教学中不仅仅只考虑形的形象性与数的抽象性,也要想到由形的直观概括出数的严密,更要利用数的严密性,来解释出形的延展性,从而建立数形结合类型题目的解题思路,洞悉挖掘图形的本质,并做到举一反三,实现思维的持续进阶。
例如:在教学人教版三年级上册《怎样拼周长最短》时,分析题意后,教师组织学生利用学具动手操作,将16个边长1分米的小正方形进行拼摆,摆成长方形或正方形,在经历拼一拼、猜一猜、算一算等一系列活动后,师生根据课堂实际操作归纳出表1:

表1 《怎样拼周长最短》归纳表格
有了用16个小正方形拼成的长方形和正方形,学生不管用最直观的数边线的方法,还是直接用(长+宽)×2进行计算都很快求出了他们的周长。根据表格,学生从不同角度观察比较发现:拼成的图形中长宽差的大小与周长息息相关。紧接着,教师带领学生思考:如果用12个小正方形去拼,他们的规律也一样吗?18个呢?学生再次探讨并归纳:用同样个数的小正方形拼成长方形或正方形,拼成的图形中,长宽差越大,他的周长越长;长宽差越小,周长越短,其中正方形的周长最短。[7]
让学生通过猜、拼、算的活动,其实也就运用“猜测—验证”的思维方法。先让学生运用拼图帮助学生解决问题,再用计算出来的具体的数量来诠释图形赋予的内涵,最后用简洁的数学语言进行描述,让结论更形象、更清晰。整个教学过程不但提升了学生的空间观念,也让学生在递进式的探究中顺着问题解决的方向逐步逼近结论,从而拓展了学生的思维。
形少数时难入微,数缺形时少直观。[8]在促进思维发展的课堂中,通过应用数形结合思想,不但可以更新教师的教学观念,改变课堂的学习方式,同时也为学生的思维活动提供丰富直观的素材,让内隐的数学思维外显。

