求解Ripa模型的保持稳定解的高阶间断Galerkin法
彭诗琪,李茂军
(电子科技大学 数学科学学院,成都 610065)
浅水波方程在地球大气、海洋、环境及水利工程和清洁能源的开发利用等领域中有广泛应用,例如海啸和风暴潮的预报,沉积物和污染物的输运,河口和近海水域的潮汐能捕捉等。Ripa[1]在1993年引入了具有温度波动的浅水波方程,这样的浅水波方程通常被称为Ripa模型。随后该模型在1995年被改进[2]。在方程中引入温度这一变量是有用的,因为流体的运动和行为通常会受到温度的影响[3]。本文考虑如下的一维Ripa模型:
(1)
其中,x表示空间,t表示时间,h表示水深,u表示水流速度,θ表示温度,b表示底部地形,g表示重力加速度。为了便于叙述,将方程(1)改写为紧凑的向量形式:
Ut+F(U)x=S(b,U),
(2)
其中
(3)
一维Ripa模型(1)有稳态解
u=0,θ=constant,h+b=constant。
(4)
对于稳态解(4),源项非零但被通量梯度精确平衡。因此,需要在离散水平上保持通量梯度和源项之间的平衡,准确地保持该稳态解。但标准数值方案通常不能很好地捕捉稳态解,并且通常会引起伪振荡。
为Ripa模型设计良好的保持稳定解的方法是一项具有挑战性的任务,因为它的稳定解比文献[3]中的浅水波方程更为复杂。在过去的几年中,有很多关于求解Ripa模型的保持稳定解的研究。第一个针对Ripa模型的保持稳定解的方法是在文献[4]中提出来的,该方法不仅较好地保持了稳定解,而且在温度跳跃点附近不会出现伪振荡。Touma和Klingenberg[5]设计了一种针对Ripa模型的二阶保持稳定解的有限元体积法。2020年,Li等[6]提出了一个新的高阶间断Galerkin(DG)方法,主要是基于流体静力学重建思想来定义一种新的数值通量,再对源项进行简单的处理,从而实现良好的保持稳定解的性质。2020年,Britton等[7]第一次提出了对Ripa模型在动水状态下的保持稳定解的高阶DG方法,他们首先选择一种新的投影算子来实现初始条件的平衡状态,然后设计新的数值通量,最后使用不同的方式分别处理稳定部分和波动部分,最终实现了算法保持稳定解的性质。
本文提出了一种高阶保持稳态解的间断Galerkin方法。该方法只需要对源项进行特殊分解,然后通过间断Galerkin法离散分解后的方程,其中对源项的一部分的离散方式与对数值通量的离散方式保持一致,只需对辅助变量选取合适的值就可以实现保持稳定解的性质。无需对数值通量做任何特殊设计,因此可以适用DG方法中现存的任意数值通量,这是本文方法的最大优势。最后通过一些数值实验来验证该方法的有效性。
1 Ripa模型的保平衡DG方法
1.1 DG方法

(5)
其中,Pk是k次多项式空间。
一维Ripa模型的标准DG方法由
(6)

(7)

1.2 源项的分解
对源项的特殊分解是保持稳定解的关键。本文对源项进行如下的分解:
-ghθbx=-g(hθ+bθ-bθ+cθ-cθ)bx
=-g(hθ+bθ-cθ)bx-g(-bθ+cθ)bx
其中c是一个预设常数。 另外,由于底部地形b(x)与时间t无关,可以将方程(1)中的h替换为(h+b),一维Ripa模型可以表示为:
(8)
一般取c为(h+b)在整个区间的平均值,即
(9)
将(8)重写为紧凑的向量形式:
Ut+F(U)x=(S1)x+S2,
(10)
其中
(11)
本文对方程(10)的离散与方程(2)的离散保持一致,其中对S1的离散方式与方程(2)中对F(U)的离散方式一致,具体的半离散格式如下所示:
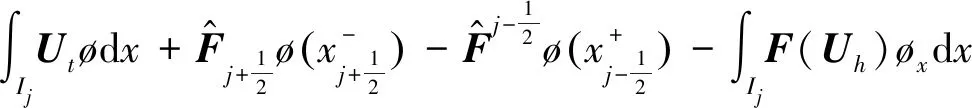
(12)
对时间离散常用的方法有单步欧拉法、龙格库塔方法、总变差递减的龙格库塔法( TVD-RK)、显式强保持稳定的四阶方法等。若采用向前欧拉法离散时间,则全离散格式如下:

(13)
为了提高时间上的离散精度和稳定性,本文采用TVD-RK法对时间离散。将方程(12)改写为常微分方程组Ut=F(U)后,其对应的三阶TVD-RK方法为:
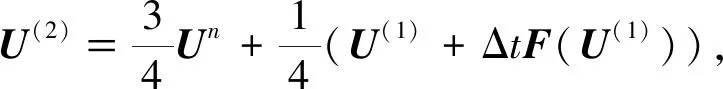
F(U)为半离散的DG模型。此外,在有不连续解出现的情况下,本文采用TVB限制器[8]来控制数值伪震荡。
1.3 平衡性分析
命题1对于一维Ripa模型的全离散格式(13),数值通量梯度与离散状态的源项相互抵消,从而精确地保持稳定解(4)。

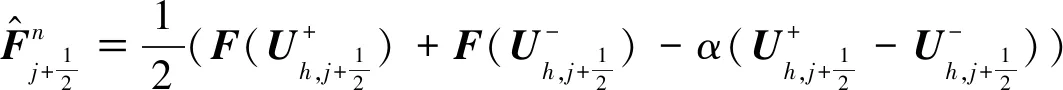
由此可知:
(14)
另外对S2有:
因此,通量梯度和源项的离散之间的残差R为:

利用(14)式和分部积分公式可以得出上式中的第三个等号。通过上式,并借助(13)式,可以得到:
2 数值实验结果
2.1 检验保平衡性质
本算例的主要目的是通过实验验证所得DG方法能够保持稳定解。在区域[0,1]上定义两种不同的底部地形。一种是间断的底部:
一种是连续光滑的底部:
初始条件满足:
h+b=10,u=0,θ=0.1。
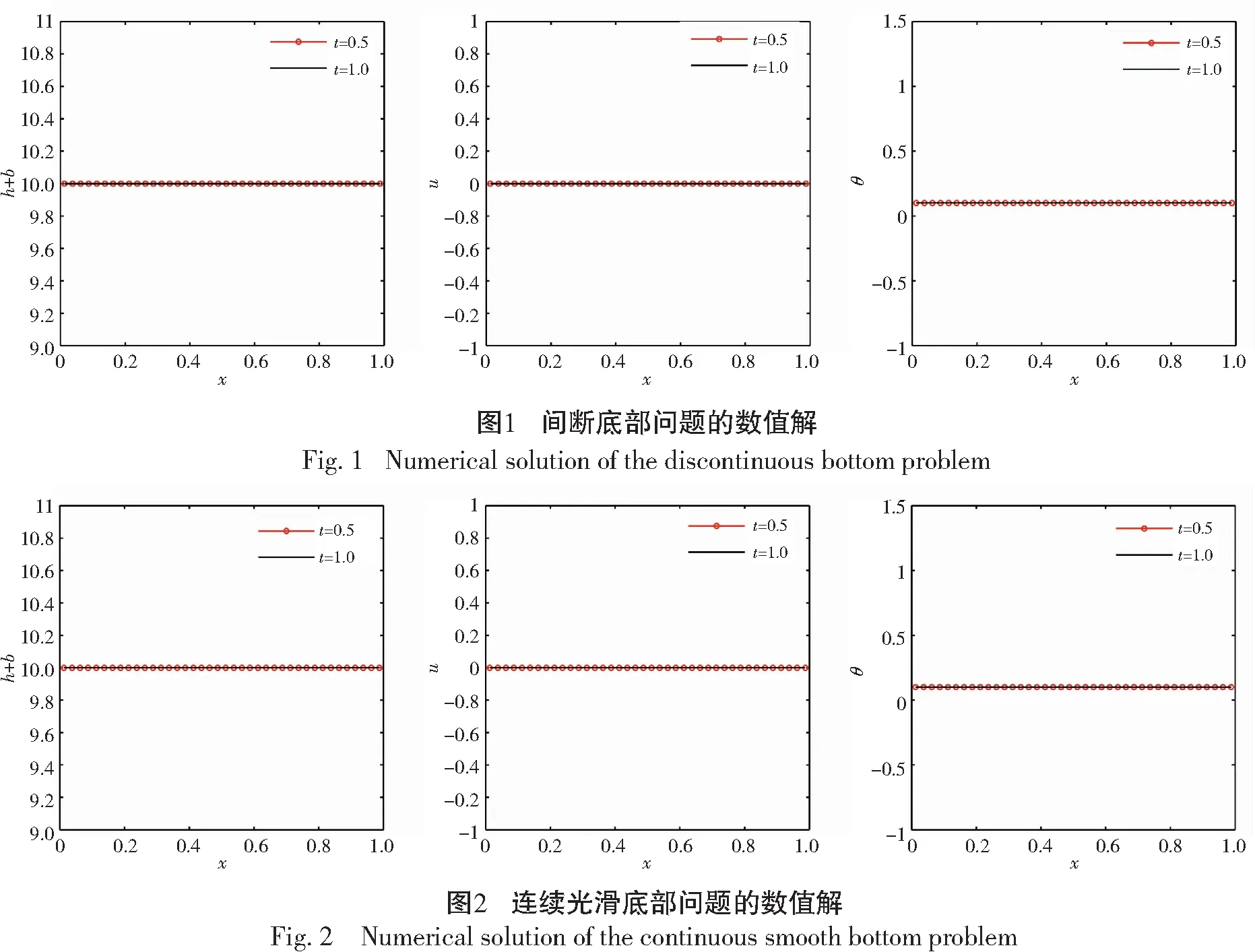
本算例分别计算至t=0.5与t=1.0,取网格点N=200。底部地形为间断底部时,h+b,u和θ的运行结果见图1。底部地形为连续光滑底部时,h+b,u和θ的运行结果见图2。从图1与图2可以看出,无论是连续光滑底部地形还是间断底部地形,使用本文构造的DG方法计算数值解时,都可以保持稳定解。
2.2 检验高阶精度
本算例用来检验本文方法的高阶精度。选取[0,1]为计算区域,采用周期性边界条件,使用一个光滑的底部地形
b(x)=sin2(πx),
初始条件满足:
算例运行至t=0.02时,结果仍是光滑的。 因为这个算例没有精确解,本文通过取N=3 200的均匀网格的数值结果作为参考解用来计算误差。 当使用线性多项式近似时,即(5)式中k=1时,h,hu和hθ的L1误差和收敛阶数见表1,h,hu和hθ的L∞误差和收敛阶数见表2,可以看出本文方法此时具有二阶精度。当(5)式中k取2时,在表3和表4中分别显示了h,hu和hθ的L1误差、L∞误差和收敛阶数。由表3和表4中可以清楚的观察到,对于h,hu和hθ,随着网格数量的增加,数值解与参考解的误差逐步减小,且可以看出数值方法是三阶收敛的。
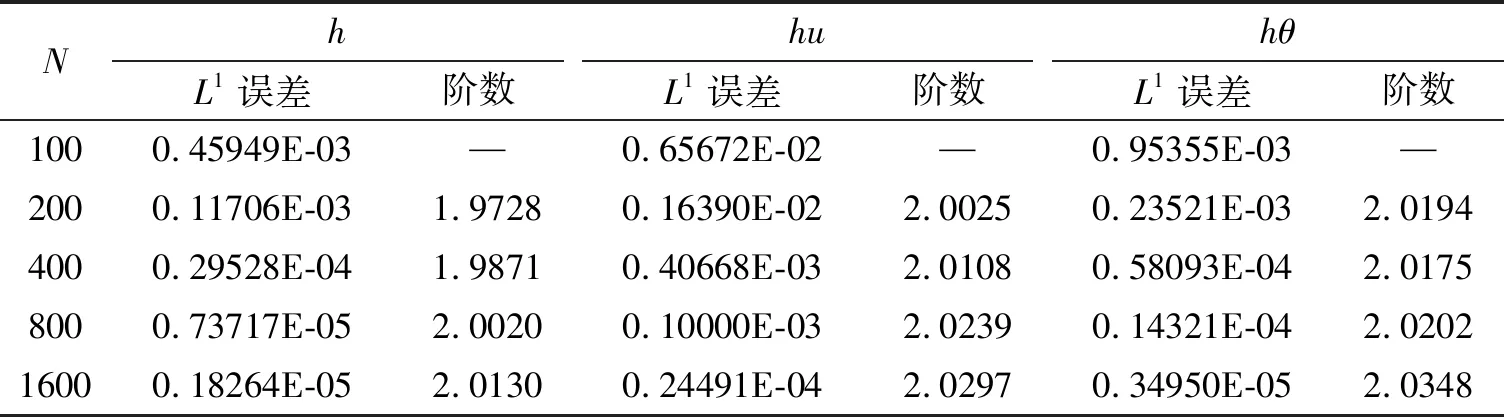
表1 k=1,t=0.02时的L1误差和收敛阶数
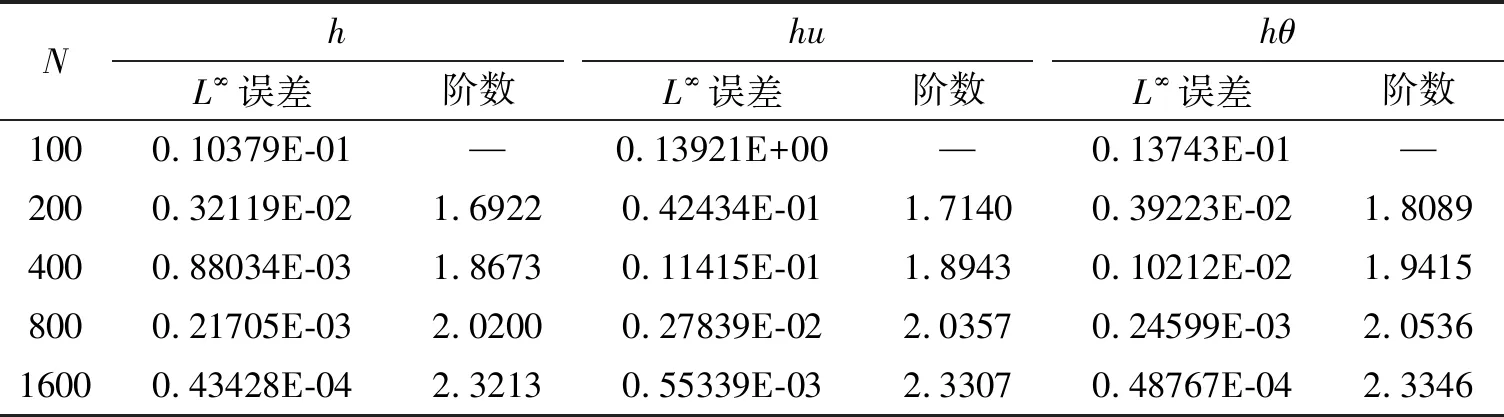
表2 k=1,t=0.02时的L∞误差和收敛阶数

表3 k=2,t=0.02时的L1误差和收敛阶数

表4 k=2,t=0.02时的L∞误差和收敛阶数
2.3 平底黎曼问题
在本算例中,考虑在平底地形(b(x)为常数)的情况下Ripa模型的溃坝问题。计算区域为[0,1],初始条件满足:
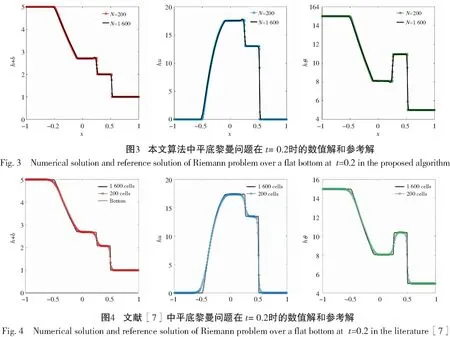
在初始时刻,大坝上游的水深为5 m,大坝下游的水深为1 m,并且上下游的水温有较大差异,底部地形绝对平坦。假设大坝瞬间溃决,使用本文方法对该问题作数值模拟,数值实验在t=0.2时结束。在图3中显示了本文方法使用200个均匀网格的数值结果,并将1 600个单元的数值结果作为比较的参考解。结果表明,数值解与参考解吻合较好。图4是文献[7]的计算结果,通过对比图3和图4,我们可以发现本文的算法与文献[7]的算法结果高度吻合,但通过仔细观察可以看出N=200时,与文献[7]的结果相比,本文的结果在间断处更加陡峭,更加贴近参考解,从而体现了本文算法的优势。
2.4 底部地形凸起溃坝问题
在本算例中,分别定义了两种底部地形。其中一个底部b(x)为矩形凸起函数
另一个底部b(x)为驼峰凸起函数
初始条件满足
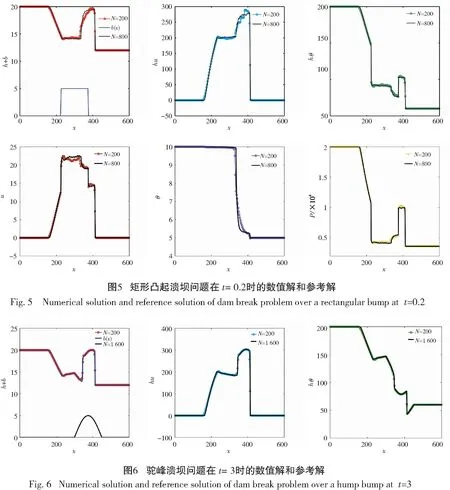
在初始时刻,大坝上游的水位高度为20 m,大坝下游的水位高度为12 m,此时的底部地形存在一个矩形凸起,凸起以外是平坦底部,同时上下游存在温度差异。假设大坝瞬间溃决,使用本文方法对该问题作数值模拟,数值实验在t=0.2时结束,计算区域为[0,600],网格N=200和N=800的数值结果见图5。可以清楚的看出数值解具有陡峭的间断过渡,即在间断解处具有良好的分辨率。
对底部地形为一个驼峰,驼峰以外是平坦底部,同时上下游存在温度差异时,假设大坝瞬间溃决,数值实验在t=3.0时结束,网格数N=200和N=1 600时的计算结果见图6。可以清楚地看出数值解具有陡峭的间断过渡,即在间断解处具有良好的分辨率。
3 结 论
本文提出了一个求解一维Ripa模型的保持稳态解的间断伽辽金法,该方法通过将源项合理的拆分为两部分,其中一部分使用与通量相同的离散方式,从而实现了保持稳定解的DG方法。本文的模型是一个不带色散项的非线性浅水波方程,但是本文的方法可以推广到更复杂的带高阶色散项的非线性水波方程[9]。本文不仅从理论上证明了数值方法能够保持稳定解,也通过数值实验验证了方法的正确性。事实上,本文的方法不仅可以对任意数值通量的DG方法都能够实现保持稳定解的性质,还可以推广到其他的高阶数值方法,例如高精度紧致差分法。

